基于神经网络算法的网络安全评价模型*

周　珑， 郭　威， 王建永， 黄杰韬

(中国南方电网 广东电网有限责任公司， 广州 510630)

当前，各种计算机病毒、木马和黑客入侵等事件接连发生，网络信息安全的局势越来越严峻.在复杂的网络环境中，如何评价和检测网络的安全风险程度，成为了信息安全领域的重要问题.很多专家和学者做出了大量的努力[1-3]，这些算法的优点在于从各个角度对网络的安全状态进行了研究，但其缺点是实用性不强.为进一步优化网络安全评价模型，回避BP神经网络算法收敛慢、搜索能力差等问题，本文引入了GA遗传算法，得出了结合这两种算法的网络安全评价模型，该模型既克服了BP神经网络算法和GA遗传算法的缺点，同时兼具这两种算法的优点，能够理想地完成网络安全评价工作.

1　评价指标设计

在复杂网络环境中，公众信息安全受到了多方面威胁，例如恶意攻击、软件漏洞、软件后门和操作失误等.为了能够准确地评估网络安全受威胁的程度，需要建立起一套综合评价指标体系.

1.1　评价指标种类

评价指标需要从层次结构、安全特性和系统安全评价体系等角度进行讨论[4].首先，目前网络的层次结构大多都是TCP/IP协议的分层模型，应用层负责用户的应用程序，其安全措施包括个人认证、加密和签名等；传输层负责用户端的进程通信，使用了安全套接字、访问控制和加密等技术；网络层负责网络的路由服务，使用了防火墙、IPSec技术；链路层负责网络中点到点的通信服务，主要用加密技术来保障安全；物理层负责实现网络中的物理连接，使用了数据流加密技术等安全措施.其次，网络的安全特性主要包括数据的保密性、完整性、可用性、可控性和不可否认性，数据的保密性是指未授权的第三方不能取得该数据；完整性保护网络中真实信息不被未授权的第三方修改；可用性能够防止人为因素对网络信息的破坏；可控性是指对内部的信息和信息系统进行监管，防止恶意代码的执行和破坏；不可否认性是指对授权的用户行为进行监控，防止用户否认自己的行为[5].最后，网络安全的评价体系主要由网络的管理安全、环境安全、硬件安全、软件安全和数据安全等方面组成，这些大的方面可以囊括网络安全的各个具体评价指标，如入侵检测和访问控制等检测指标.

1.2　设计原则

在设计评价指标时，还必须遵循以下原则：

1) 完备性.网络安全评价指标应该全面、完整和有效刻画出网络安全的基本特征，得出精确可信的评价结果.

2) 独立性.评价指标之间经常会有或多或少的相关性，设计人员应该尽量减少多个指标的联系，提高评价的准确性.

3) 简要性.优良的评价指标能够简明扼要地反映网络的安全水平.

4) 可操作性.指标设计必须切合实际，涉及数据的收集和处理过程简单易行.

1.3　评价指标体系

为建立科学的评价指标体系，本文引入了德尔菲法(Delphi)，该方法使用了背对背的方式咨询专家小组的意见，小组成员匿名发表意见，同时成员之间不允许相互讨论，通过这样多轮的反复询问和反馈修正，得到集中的预测意见，从而总结出符合实际情况的预测结论.这种方法也叫专家意见法，具有匿名性、反馈性和优良的统计特性，能够结合多个专家主观意见和客观规律，可以对大量无法定量分析的指标进行相对准确的估算.首先确定专家小组的所有成员和若干评价指标，制作出成员需要填写的咨询表格，然后进行首轮初步咨询，并计算需要统计的参数，进行多轮咨询并反复修正专家意见，最后统一专家成员的意见，本文使用德尔菲法流程图如图1所示[6].

图1　德尔菲法流程图Fig.1　Flow chart of Delphi method

在德尔菲法的作用下，经过系统分析和对专家评分的统计，选取出的指标形成了本文评价模型的完整指标体系，该体系结构如图2所示.

2　算法模型

神经网络(BP)算法是一种借鉴人体神经元结构来进行信息处理和计算的智能算法，具有高度的自组织性和自学习性等优点，善于处理推理、判断等问题，但该算法也存在收敛速度慢、容易陷入局部极小值和网络泛化能力差等缺点[7-8].为了避免BP算法的上述缺陷，本文引入了GA遗传算法，将这两种算法结合到一起来进行计算，并对网络的安全程度进行计算和评价.在算法中，令E为目标函数，w和v分别为输入层到隐含层、隐含层到输出层的权值矩阵，θ和r分别为对应的阈值矩阵，m为输入层的数量，n为输出层的数量，p为隐含层的数量，则GABP算法的数学表达式为

图2　网络安全评价指标体系Fig.2　Network security evaluation index system

(1)

如上所述，GABP算法的输入层x∈Rm，输出层y∈Rn，输入层到隐含层的权值矩阵w∈Rm×p，阈值矩阵为θ∈Rp，隐含层到输出层的权值矩阵v∈Rp×n，阈值矩阵为r∈Rn.设隐含层h∈Rp，则输入层到隐含层的关系为h=xiwi+θi，且隐含层到输出层的关系为y=hvi+ri.其中，算法需要优化的对象是w、θ、v和r.

2.1　目标函数

(2)

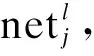
1) 大致选定权值矩阵等初始值；

2) 直到误差指标Ek小于某一设定值，否则重复步骤3)；

(3)

该算法的变异运算使用均匀变异的方法，即个体在变异时，仅随机改变个体向量中的某个分量，得到的新个体必须具有更小的目标函数值才能取代变异前的个体，如果不是，则个体保持不变，其数学表达式为

(4)

2.2　算法步骤

本文算法的归纳步骤如下：

1) 初始化，按照上文中提到的算法来得到初步解(w，v，θ，r)，设定遗传进化代数k、输入矩阵X、目标函数值E、遗传最大代数N、交叉概率Pc和变异概率Pm.

2) 如果目标函数值E<ε(ε为常数)，跳转至步骤6)；否则，设定k=0，跳转至步骤3).

3)k=k+1，如果k≥N，跳到步骤5)；否则，计算当前解的目标函数值E.

4) 以交叉概率Pc和变异概率Pm随机对当前解进行交叉或者变异运算，得到备选解，然后使用轮盘赌选择方法对当前解和备选解进行评估和对比，生成目标函数值更小的新一代个体，跳转至步骤3).

5) 输出第N代个体，同时计算目标函数值E，跳转至步骤2).

6) 输出最终解.

3　仿真与分析

在网络安全评价研究领域，评价结果可以分为A(很高)、B(高)、C(一般)、D(低)4个等级，设满分为1分，这些等级的评分分布如表1[10]所示.

表1　安全等级评分分布Tab.1　Distribution of safety level scoring

为验证GABP算法的可行性和执行效率，本文使用Matlab平台进行仿真.在具体仿真前，BP神经网络算法必须先使用多组数据进行训练，之后才能使用训练完成的神经网络进行评价.在本文中多组网络安全指标数据被用来训练神经网络.在仿真过程中，5组输入数据(每组数据C1～C17)和期望输出数据被用来进行具体的仿真评价，在执行过程中，上述算法被编译成Matlab程序脚本，首先神经网络进行了8 000多次训练，其输出误差最终达到收敛.

在神经网络算法仿真中，隐含层的节点数是一个重要参数.理论证明，如果隐含层节点数增加到一定程度，BP神经网络算法的训练误差可以无限逼近0.在仿真过程中，本文针对不同隐含层节点函数，使用GABP算法对相同数据进行训练，根据其仿真结果得到不同隐含层节点的训练误差与预测误差，分别如图3、4所示.

由图3可知，随着隐含层节点数的增加，评价算法的训练误差在不断下降，最后趋近于0，在节点数达到5之后，其下降速率就会增强，这说明隐含层节点数的增加可以增强算法的学习能力.由图4可知，随着隐含层节点数从2增加到5，评价算法的预测误差急剧降低，隐含层节点数从5增加到7时，其预测误差基本不变，隐含层节点数继续增加时，预测误差会急剧增加.这意味着隐含层节点数在比较小的时候，评价算法的预测能力会随着节点数增加而增强，然而节点数增加到一定程度时，算法中的神经网络会产生过度吻合，即节点太多反而令噪声增加，这时算法的预测能力下降.综上所述，为了令评价算法的训练误差和预测能力达到相对理想的状态，隐含层节点数最好设置在[5，7]之间.本文神经网络的隐含层节点数设置为5，学习精度设置为0.001，其仿真使用数据如表2所示.

图3　不同隐含层节点数设置的训练误差Fig.3　　　　Training error of number of nodes in different hidden layers

图4　不同隐含层节点数设置的预测误差Fig.4　　　　Prediction error of number of nodes in different hidden layers

表2　仿真使用数据Tab.2　Data used in simulation

本文网络安全仿真结果如表3所示.表3中评分是根据目标函数值E计算得出的，其计算公式为

结果表明，该模型的最大相对误差为3.7%，实际输出与期望输出基本一致，所有的网络安全等级为B，网络的安全程度较高.

另外，将本文的算法与BP算法和遗传算法进行了误差比较，比较结果如表4所示.通过对比可以发现，本文算法的评估精度均高于BP算法和遗传算法.

表3　仿真结果Tab.3　Simulation results

表4　BP、GA与GABP算法的误差比较Tab.4　　　　Comparison in error of BP，GA and GABP algorithms　%

4　结　论

本文在分析神经网络算法和遗传算法的基础上，通过优化组合提出了能够评价网络信息安全的GABP算法，并对该算法的评价功能进行了逼近实际的仿真.仿真结果表明，本文所提出的GABP算法性能优于BP算法和遗传算法，可以准确地评价出网络的信息安全程度.综上所述，GABP算法可以科学评价安全指标体系，并可以使用网络实时监控数据，定量地评价出网络的信息安全状况，为未来网络信息安全研究提供了参考.