从正三角形的旋转与反射谈起
2018-07-16赵德科张英伯
赵德科 张英伯
(北京师范大学珠海分校应用数学学院 519087)(北京师范大学数学科学学院 100875)
1 引言
我们曾经为中学的数学兴趣小组讲解过最浅显的群论知识.目前的小学数学已经加入了部分平面几何,渗透进旋转和反射的概念,并反复提及,直到初中.于是我们从旋转和反射入手,为喜欢数学的孩子引入了群的概念,效果似乎不错.
在这里,愿意把我们的讲稿与诸位老师分享,共同探讨在数学英才教育中怎样为爱好数学的学生建立更适合他们的学习环境,以求抛砖引玉.
2 保持平面图形不变的旋转与反射
我们在数学课上探讨过平面图形的旋转:将平面围绕一个定点旋转任意给定的角度,那么图形S就随着平面的运动变到了图形T.在这里我们只观察一种特殊情况,即选择一个特殊的图形和一个特殊的点,使得平面围绕该点旋转某个角度之后,图形T与原图形S重合.同学们可能立刻想到,最容易做到这一点的图形S是圆,只要选择圆心作为定点,那么平面围绕圆心旋转任意角度后,所得到的圆T都与圆S重合.
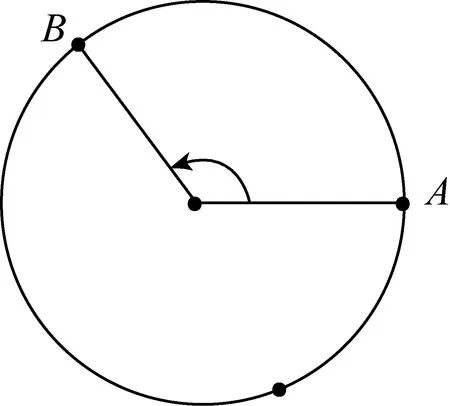
为了进行下面的讨论,先解释一下“反射”这个名词.可能为了更形象一些,我们的中小学教科书上把它叫做“翻折”,在这里就按照数学上的叫法,称为“反射”,即给定平面上的一条直线,将平面沿这条直线翻转180°,平面上的一个图形S就变成了图形T.在此我们只讨论一种特殊情况,即选择一个特殊的图形和一条特殊的直线,使得平面沿该直线翻转180°以后,图形T与原图形S重合.同学们也会立刻想到,最容易做到这一点的图形S还是圆,只要选择过圆心的任意一条直线,平面沿该直线翻转180°以后,圆T与S重合.因此,圆被认为是一种对称性最强的图形.
那么除了圆以外,有没有什么直线图形,比如我们熟悉的三角形、四边形、甚至多边形是否有较强的对称性呢?我们下面以正三角形和正方形为例说明:正多边形具有较强的对称性.当然正多边形的对称性远远无法和圆相比,因为圆可在平面绕圆心旋转任意角度,沿任一过圆心的直线反射后仍然与原图形重合,而正多边形只能在有限多种旋转和有限多种反射下与原图形重合.
3 正三角形和正方形的旋转与反射
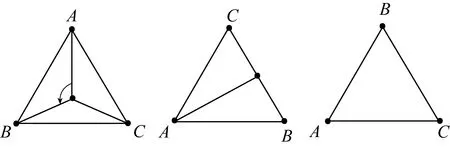
平面正三角形在以平面的哪个点为中心,多少度的旋转下与原图形重合呢?我们知道正三角形的三条高线、中线、角平分线分别重合,于是它的垂心、重心、内心三点重合,通常称为正三角形的中心,记作点O.容易看到,当平面围绕正三角形S的中心O逆时针旋转120°或240°时,所得到的正三角形T与S重合.当然若平面旋转 360°时,平面上所有的图形仍然回到原来的位置(见下图):

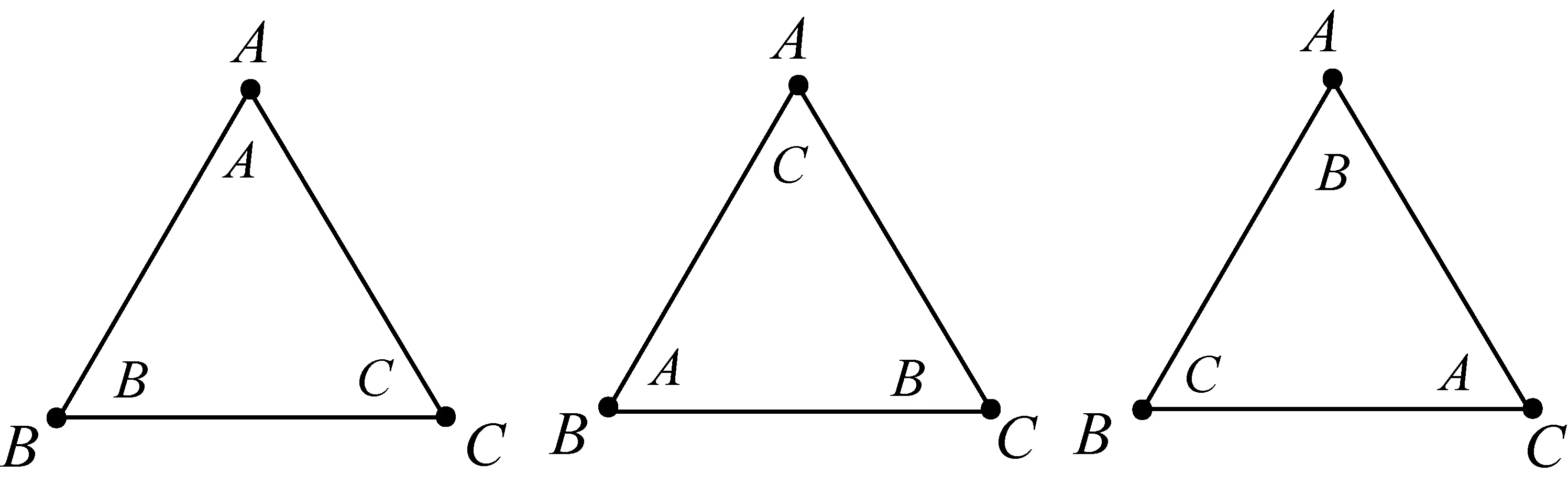
如果将原三角形的顶点依次记作A、B、C,那么逆时针旋转120°后,A、B、C三点分别转到了原来B、C、A的位置;旋转240°后,则A、B、C三点分别转到了C、A、B的位置;若平面不动,那么三个顶点A、B、C的位置也没有动(见下图):
接下来,我们考虑平面的反射:给定正三角形S,我们选取适当的直线,使得正三角S所在平面沿该直线反射后得到的正三角形T与S重合.同学们很容易想到,该直线必是过S的某一顶点与中心O的直线,且平面沿连接中心O点与任意一个顶点的直线L进行反射后,所得正三角形T与S重合.从而正三角形S只有三种不同的反射(见下图):
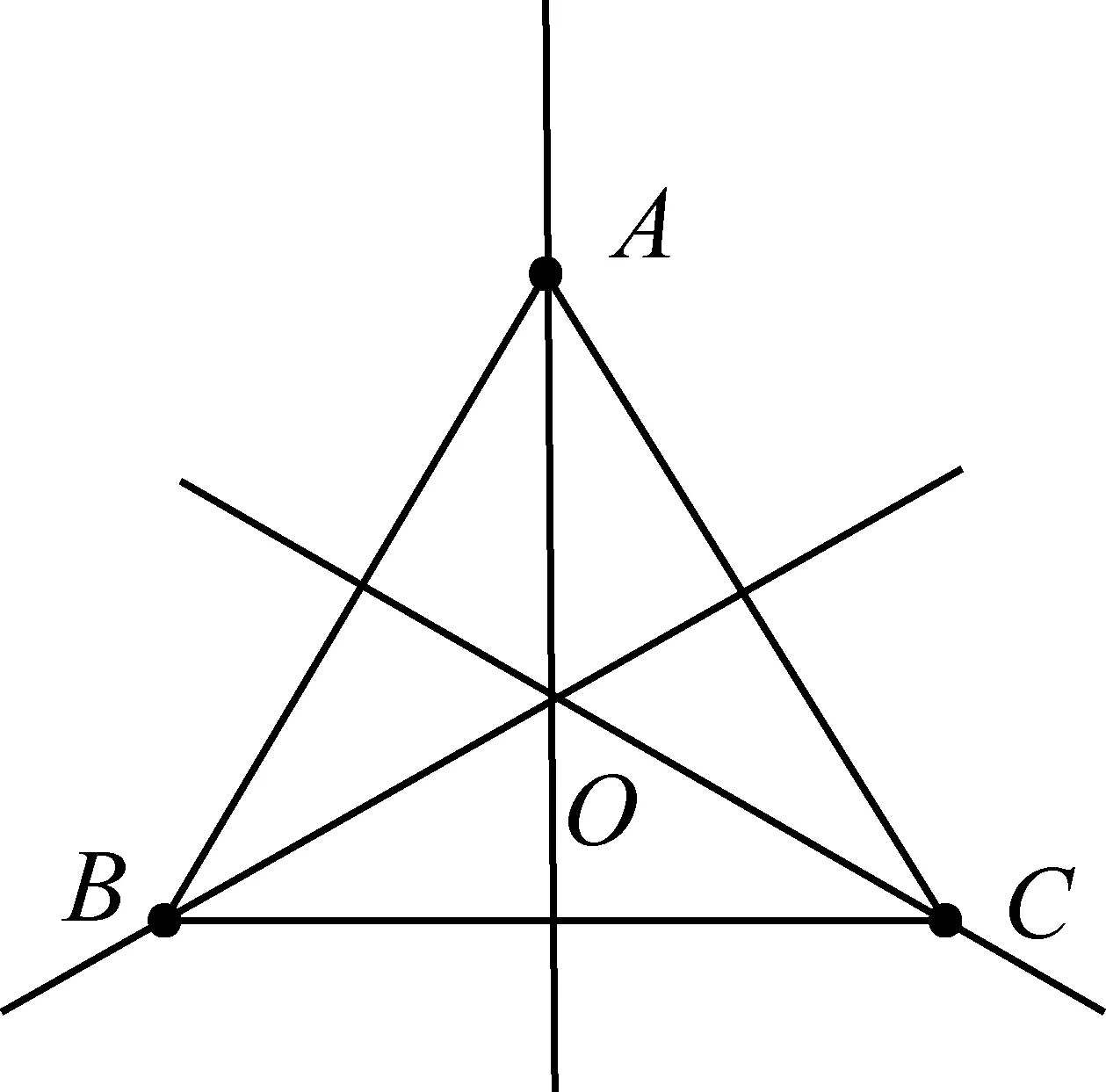
且经过沿直线AO、BO、CO的反射后,分别得到以下与S重合的正三角形T:
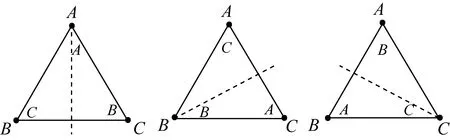
易见,经过上述三种反射,原来的顶点A、B、C分别变成了A、C、B;C、B、A;B、A、C.
第三,进一步有效开发社区内教育资源。现有社区资源的有效利用能够更加快速有效地推进资源建设。从无到有是总量的增加,其附带的变化因素颇多,但是从有到精,充分利用已有资源来创造优良的教育环境,意义要大于前者。通过现有资源的变革和创新,教育模式的重构和整合,以挖潜、扩充的手段不断拓展资源容量,社区的教育会更加良性发展。
下面我们来考虑正方形ABCD.将两条对角线AC与BD的交点记作O,称为正方形的中心.我们先来研究平面的旋转变换:
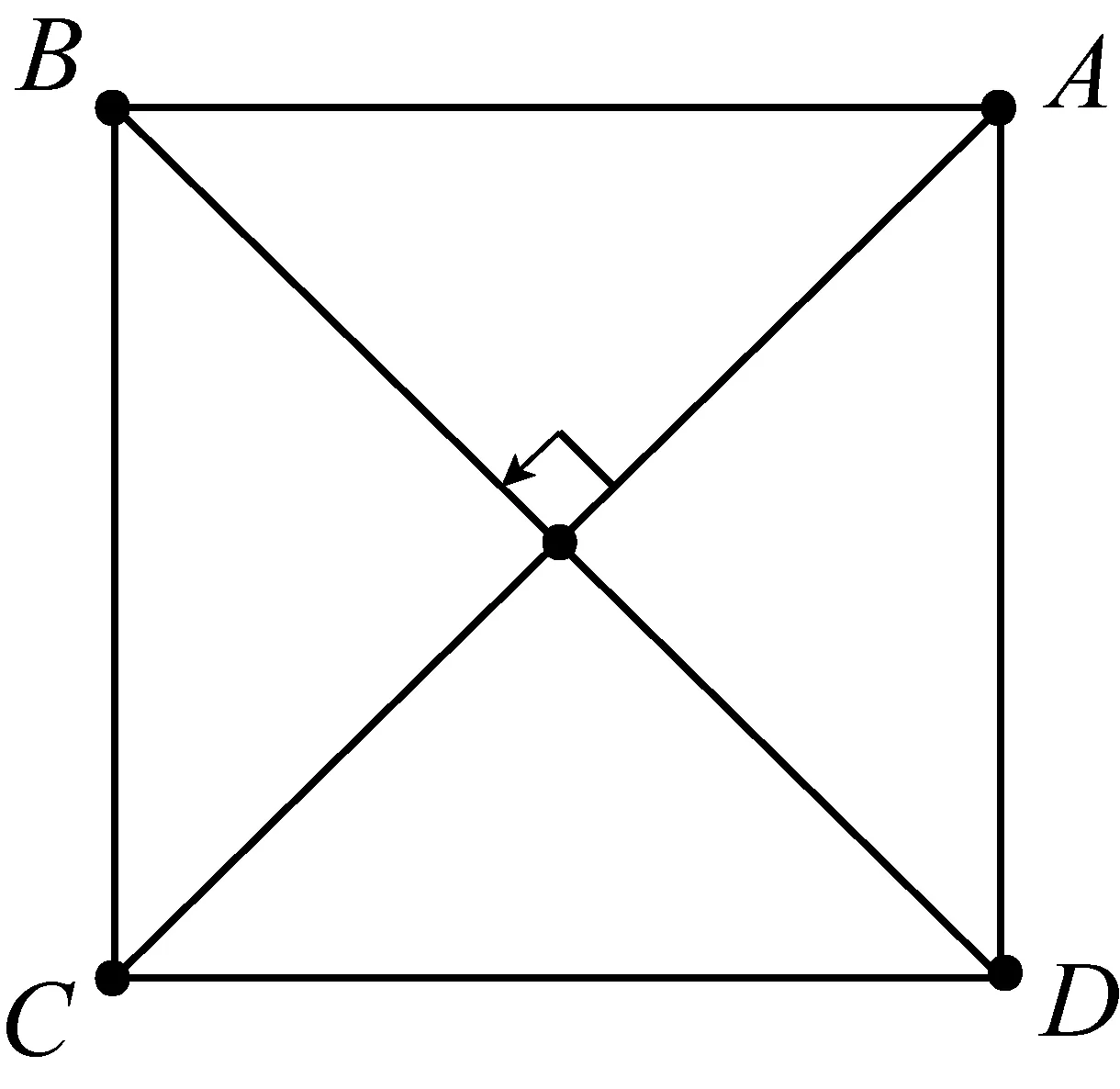
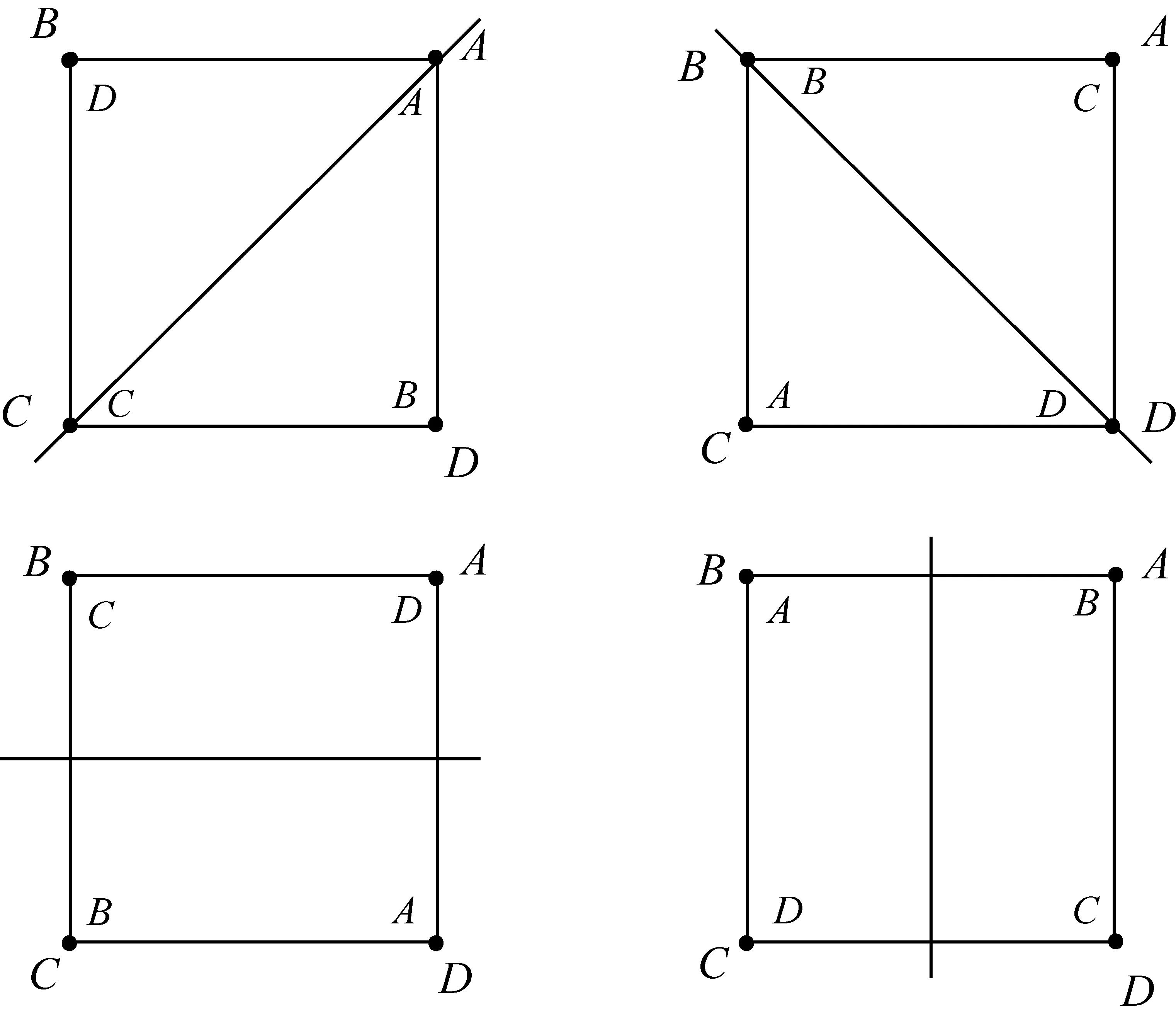
当正方形围绕中心O分别逆时针旋转90°、180°、270°的时候,ABCD点分别转到了原来点BCDA、CDAB、DABC的位置.当然旋转360°时平面上所有的点回到原位,见下图.

这时,正方形ABCD的原顶点位置与平面绕O点逆时针旋转0 ° 、90 ° 、180 ° 、270 °旋转后顶点位置的对应关系是:
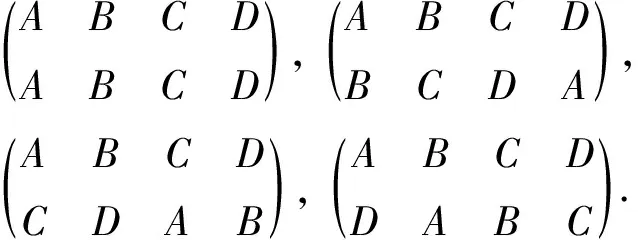
下面考虑平面的反射变换.显然,当平面沿正方形的两条对角线,或者过中心的水平、竖直两条直线进行反射后,所得正方形与原正方形重合.
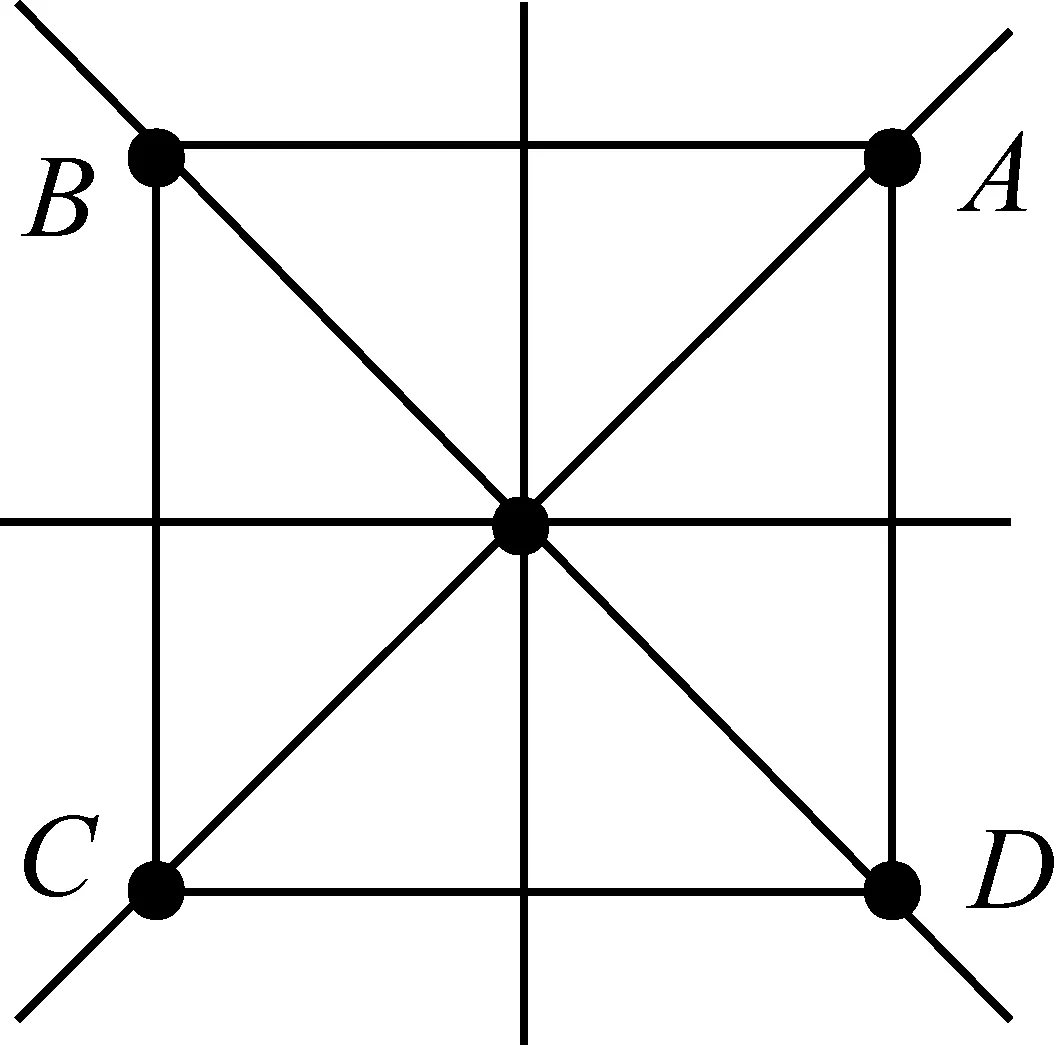
正方形ABCD的原顶点与分别沿直线AC、BD、过O点的水平线以及过O点的竖直线反射后顶点的对应关系为:
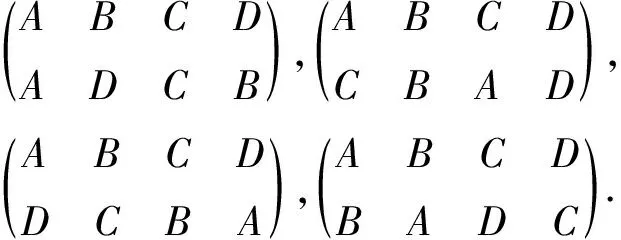
4 旋转与反射的合成
特别有趣的是,将正三角形的三个旋转和三个反射,一共六种变换放在一起,构成一个团队,或者用数学语言称为一个集合.那么进行其中任意一个变换后再接着进行任意一个,其结果仍然在此集合中.譬如旋转120 °后,再接着转120 °,那么就相当于转了240 °;若是接着再转120 °呢,则相当于回到了原来的位置.该事实可用前面约定的数学符号表示为如下等式
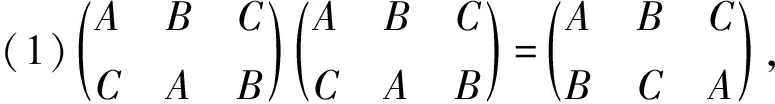
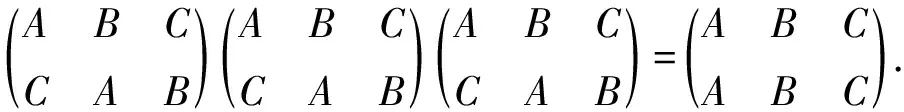
如果旋转120°之后再进行一次反射呢?比如(见下图):
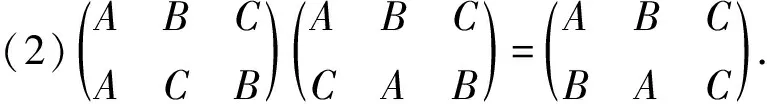
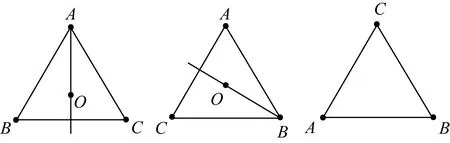
那么进行两次反射后可以得到什么结果呢?如先沿直线AO反射,再沿直线BO反射,竟然得到了一个围绕中心点O的120°旋转(见下图):
上图可用符号表示为等式:
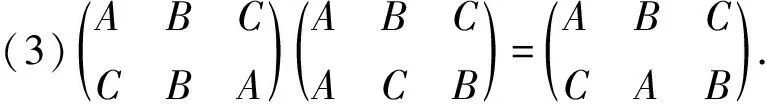
上述事实(1),(2),(3)通常简称为该集合对旋转和反射的合成封闭.遗憾的是,我们无法在这里进行严格的数学证明,一是时间不允许,二是作为中学生,我们的基础知识还不够.如果有兴趣,我们可以在课后试试正三角形六种变换中任意两种的合成,以及正方形八种变换中任意两种的合成,就可以发现它们无一例外,都满足这个规律:即合成的结果仍然落到该集合中,或集合对于合成运算封闭.
正三角形的旋转和反射六种变换,它们构成的集合在变换的合成之下封闭.在数学中,这些变换的集合连同它们的合成称为正三角形的二面体群,记作D3.如果将旋转变换用希腊字母ρ表示 并把旋转角度写在字母的右下角;将沿AO、BO、CO轴的反射变换分别记作τ1、τ2、τ3,那么
D3={ρ0,ρ120,ρ240,τ1,τ2,τ3},
且其中变换的合成仍然在集合中.正方形的八种变换也有同样的性质.变换的集合连同变换的合成称为正方形的二面体群,记作:
D4={ρ0,ρ90,ρ180,ρ270,τ1,τ2,τ3,τ4},
其中变换的合成仍然在集合中.
在D3和D4中,有一个非常特殊的变换ρ0:它与任意变换的合成,或者任意变换与它的合成,都得到那个变换本身.事实上,ρ0是一个保持平面上任意一个点都不动的变换,在数学上叫做恒等变换.
还有一个有趣的事实是:在D3中,对于任意一个变换,我们都可以找到一个变换,使得它们的合成为恒等变换,并且可以交换次序.例如:ρ120ρ240=ρ0=ρ240ρ120;τiτi=ρ0, 对于i=1,2,3皆成立;最后ρ0ρ0=ρ0.当然,同样的事实对D4也是对的.
同学们都知道整数、有理数、实数的加法有结合律,变换的合成也有结合律.遗憾的是,与通常数的加法和乘法不同,变换的合成没有交换律.例如:上面的公式(3)证明了在D3中,τ2τ1=ρ240,但是τ2τ1=ρ240.显而易见,对于任意大于2的正整数n,我们也有正n边形的二面体群.
事实上,除了正n边形的对称变换构成群之外,还有很多很多带有某种封闭运算的集合满足上述四个条件,运算的合成通常称为乘法:即(1)乘法结合律成立;(2)有单位元;(3) 任意元素都有逆元.这样的集合及其运算组成的代数结构称为群.
5 群论的起源
群的概念是由挪威数学家Abel和法国数学家Galois在19世纪20—30年代提出来的,他们为了高次方程的求解问题用到了群结构.更早些年,拉格朗日就已经开始考虑这个问题了,并且也用到有限群,但是没有成为系统.
在十六世纪的意大利文艺复兴时代,那里的数学家已经给出了三次和四次方程的求根公式.而五次方程的求根公式,成为困扰数学界300年的难题.Abel证明了五次和五次以上的高次方程没有根式解,也就说,不能用我们学过的二次方程求根公式那样,对五次或五次以上的方程写出一个用加、减、乘、除和开方这五种运算符号给出的公式.证明用到了方程根的“置换群”.
Abel于27岁因贫病交加早逝后,Galois 最终确定了代数方程可以用根式解的充分必要条件,彻底解决了高次方程的求解问题.也就是说,什么样的高次方程可以用根号解,什么时候不可以.因而被史家称为现代代数学的奠基人,也是群论的奠基人.
Galois生于1811年,12岁之前由母亲教他读书,12岁进入巴黎甚至法国最优秀的圣路易大帝中学.他热爱数学,并痴迷其中,14岁就读了很多大数学家的论文.16岁报考著名的巴黎高等工业学校,那所学校有众多伟大的法国数学家.由于桀骜不驯的性格,他在面试时与主考官发生冲突,结果名落孙山.第二年仍然没有成功,不得不屈尊就读当时名气不大的巴黎高等师范学校.刚入校他就发表了四篇数学论文.18岁那年,他将有关解方程的两篇论文呈送法兰西科学院.文章交到伟大的柯西手中,结果被弄丢了.19岁时他再次递交了一份仔细写成的研究报告,由伟大的傅里叶审查,不幸的是后者很快过世,论文遗失.在那个年代,法兰西全国动荡,革命频仍.作为热血青年的Galois深陷其中.他因批评巴黎高师学监对革命不支持遭到开除,又因政治罪两次被捕,在狱中度过了他成年后的半生和最后一年的大部分时光.Galois在1832年的一次决斗中被枪杀.在决斗的前夜,Galois将毕生的研究匆忙写成了一个说明交给他的朋友,最终保留下来.
Galois去世后,虽然有两位法国数学家整理和介绍过他存世的文章,但因他的思想太过深奥,始终不能被数学界接受.直到40年后,法国数学家若尔当在他的一本著作中全面而清晰地阐述了他的工作,数学界才最终理解了Galois理论.Galois本人也作为近代代数学的创始人受到世界各国数学界的敬重.
到了信息时代的今天,群的理论和思想不但广泛应用于物理、化学、生物等各个基础学科,也渗透到基因检测、材料科学、工程设计等广泛的应用领域.当然,群论更是现代数学研究中最基本最重要的对象之一.
