水平井三元复合驱流入动态耦合模型研究
2018-07-16姜振海
姜振海
(大庆油田第三采油厂,黑龙江 大庆 163000)
三元复合溶液是指碱、表面活性剂和聚合物按一定配方混合组成的复合体系(ASP体系)。三元复合驱技术可以提高驱油效率,降低采出液含水率,提高采出程度。水平井技术作为一种高效的采油手段,因其能够增大控制面积、提高单井产能、抑制锥进及提高采收率,已被广泛地应用于低渗透油藏、多层油藏、薄层油藏、稠油油藏,水平井与化学驱结合可以充分发挥两者的优势,提高产量。三元复合驱技术目前大多数都是在直井注采井网中应用,三元复合驱在水平井注采井网的应用仍处于矿场实验阶段。本文通过建立水平井三元复合驱流入动态预测模型,对现场进行水平井三元复合驱产能预测及参数控制提供了基础。
1 三元复合驱溶液流变参数确定
三元复合溶液由于包含聚合物,呈现出非牛顿流体特性。三元复合物溶液在地层中渗流时不仅体现黏性特征,而且在通过孔喉时会呈现较强的弹性效应[1-2]。同时三元复合溶液的组成要比单一溶液多样,各个组分配置比例不同会影响三元复合溶液的流变参数,因此三元复合溶液在地层中渗流时呈现比较复杂的流变性质。
1.1 三元复合驱溶液的稠度系数和流性指数

(1)
n(x)=n
(2)
式中,n为三元溶液在注入井的流性指数;x为地层一点距采出井的距离,m;rw为采出井井筒半径,m;Kw为三元溶液在注入井的稠度系数,mPa·sn;L为渗流总长度,m;a为中间变量,a=ln(Kp/Kw)/(1-L/rw),Kp为三元溶液在采出井的稠度系数,mPa·sn。
1.2 三元复合驱溶液的黏度
三元复合驱溶液属于黏弹性流体,溶液在地层渗流时,既存在黏性压降,又存在弹性压降,而且由于连接孔隙体的孔喉直径相比孔隙体很小,黏弹性流体很难通过孔喉,因此会在孔喉处产生比黏性压降大十几倍的局部压力损失,导致注入井的注入压力很高,但是这种弹性压降也是提高孔喉残余油驱替效率的重要机理之一[7-8]。三元复合驱溶液在地层渗流时的黏度包含剪切黏度和弹性黏度:
μeff=μe+μv
(3)
式中,μv为描述其黏性特征的剪切黏度,μe为描述其弹性特征的弹性黏度。
ASP体系及ASP-原油乳状液在多孔介质中的剪切黏度符合幂律模式:
μv=Kγn-1
(4)

(5)
式中,γ为流体在地层渗流的剪切速率,1/s;v为渗流速度,m/s;φ为地层孔隙度。
地层孔隙模型采用变截面收缩为扩张通道模型,曹仁义等[9]得到了黏弹性三元复合溶液通过变截面喉道的总压降公式为:
(6)
定义w为多孔介质渗流中弹性压降和黏性压降之比,则:
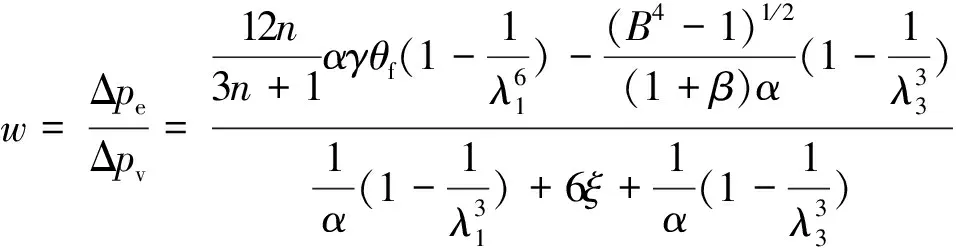
(7)
黏弹性三元溶液在多孔介质渗流时的有效黏度为:
(8)
2 三元复合驱渗流模型
三元溶液在地层中的流动符合广义达西定律:
(9)
式中,k为渗透率,mD。
联立式(5)、(8)、(9)得:

(10)
根据S. D. Joshi[10]推导水平井产能公式的思想,将流体在地层中的渗流分为水平径向渗流和垂直平面径向渗流。根据幂律流体表皮系数的定义,考虑表皮系数的水平井产能公式为:
(11)

(12)
3 三元复合驱井筒变质量压降模型
由于水平井的水平段比较长,在生产阶段,沿水平段不断有流体流入,则井筒中的流量从趾端到跟端不断增加,为变质量流动,在水平井段不同位置的流体流速也不同,同时流体从壁面的流入会与井筒中的主流相互干扰,引起井筒壁面流态的变化,这些现象都会改变沿井筒的压力分布[11]。水平井筒变质量流压降的计算与常规管流不同,沿程流体流动的压降主要由摩擦压降、加速度压降、混合压降、重力压降等几个部分组成,并受到完井参数、井筒壁面注入比、流体组分等多种参数的影响[12]。
汪志明等[13]推导了水平井筒变质量流的压降模型:
=Δpacc+Δpwall+Δpg
(13)
其中:Δpacc为井筒加速度压降,Pa;Δpwall为井筒壁面摩擦压降,Pa;Δpg为重力压降,Pa。
加速度压降计算公式与常规油水的计算公式相同,壁面摩擦压降Δpwall在不同的井段由于流速的不同可分为层流摩擦压降和紊流摩擦压降。井筒中三元复合溶液的流态可以根据雷诺数来判断:
(14)
幂律流体在管流中的有效黏度为:
(15)
由式(14)和(15)可得到判断幂律流体流态的广义雷诺数为:
(16)
由于三元溶液的黏弹性,三元溶液从层流到紊流转变的临界雷诺数比牛顿流体的大,一般在4 000以上,其更精确的值可通过实验值确定。
(1) 对于层流流动,可用牛顿流体的摩擦压降来表示非牛顿流体的摩擦压降:
(17)
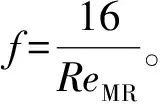
淮山中含有丰富的多糖、蛋白质、尿囊素和胆碱等多种生物活性物质,具有调节免疫、抗氧化、抗衰老、降血糖等功效。
将式(16)代入式(17)可得圆管层流摩擦压降公式为:
(18)
(2) 对于紊流流动,Fanning摩擦系数采用
Dodge-Metzner 公式:
(19)
4 水平井流入动态耦合数学模型
由于水平井筒中存在压降,每一点的压力不同,导致井筒每一点与地层的压差不同,每一点流体从地层到井筒的流量不同,而从壁面流入的流量大小也会影响水平井筒内的流体流动,从而影响流体的压力分布,因此流体在地层的渗流与流体在水平井筒内的流动在井筒壁面存在一个耦合的过程,在井筒壁面相互影响。
根据势的叠加原理建立水平井流入动态耦合数学模型,地层中一点的势计算公式为:
(20)
对式(20)两边求导得:
(21)
(22)
可求得平面上一点势的表达式为:
(23)
在井筒壁面,流体在地层中和流体在井筒中保持压力相等,质量守恒。定井底流压生产时边界条件为:pwfww,0=pwf。
联立油藏流动方程与井筒压力方程得耦合模型为:
A1X1=b1,A2X2=b2
其中:
X2=[pwf1,pwf2,…,pwfm-1,pwfn]T
5 模型精度验证
模型需要的参数取值如表1所示。不同驱替阶段的注入压力和注入流体的稠度系数和流性指数如表2所示。
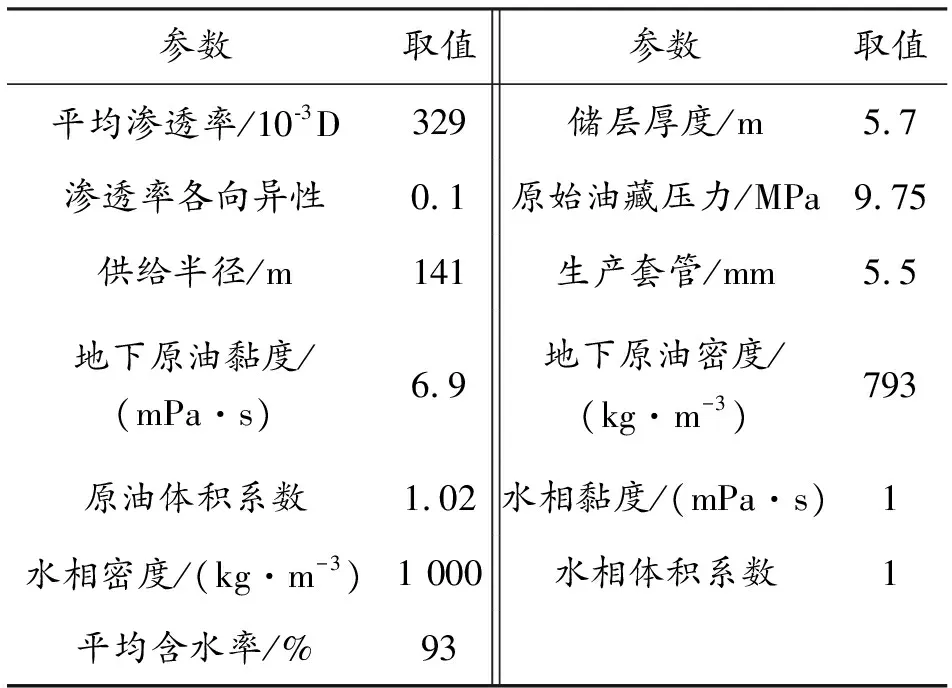
表1 模型计算参数Table 1 The parameters used in the model

表2 不同驱替阶段注入压力和流变参数取值Table 2 The values of injection pressure and rheological parameters of different flooding periods
在三元复合驱过程中,随着不同驱替段塞的注入,注入流体在地层中渗流的阻力越来越大,因此导致不同注入阶段的注入井的压力不断升高,不同注入阶段流体的流变参数也不同,因此需要对不同注入阶段计算不同的流入动态曲线[14]。根据大庆油田目前投产的一口三元复合驱水平井的生产数据,对计算IPR曲线进行了精度验证,结果如图1所示。表3为水平井不同驱替阶段实测数据平均值和计算值的误差表。可以看出,水平井三元复合驱产量预测与实际生产数据的精度符合率达到78.6%,基本符合现场要求。


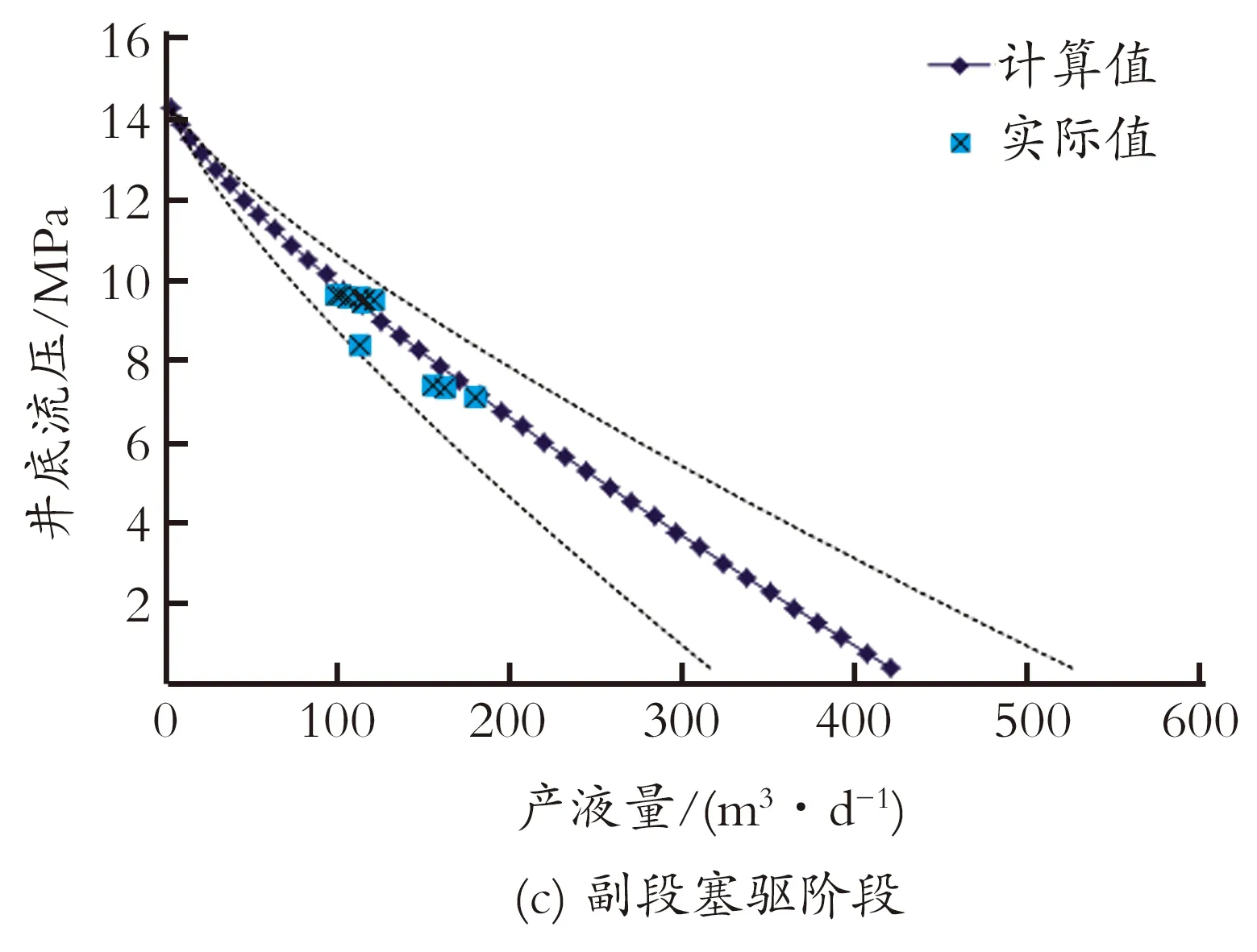

图1 不同聚合物驱阶段计算IPR与实际生产数据对比Fig.1 The comparison of calculated IPR with actual production data in different flooding period

表3 不同驱替阶段计算值与实测平均值误差Table 3 The relative error of calculated values with average actual production data in different flooding periods
6 产能影响因素分析
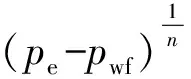


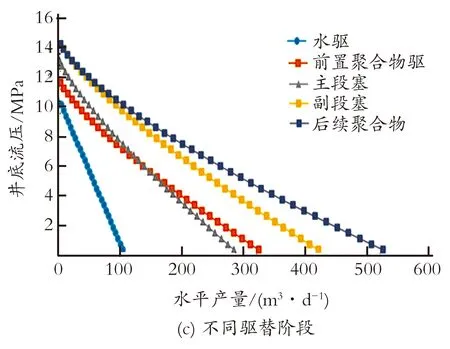
图2 不同流性指数、稠度系数和驱替阶段下的IPR曲线Fig.2 The IPR curves of different n,K,flooding periods
7 结论
(1) 考虑三元复合溶液不同驱替阶段的流变性,建立了水平井产能预测模型,三元复合驱生产油井的IPR曲线是上凹的。相同井底流压下,随着流性指数和稠度系数的增加,水平井产量降低。
(2) 不同驱替阶段的注入井的压力不同,因此不同驱替阶段的IPR曲线不同,产量预测时要选择对应的动态曲线。
