抑制抖振的医疗机械臂轨迹规划方法与仿真
2018-07-16黄相锦
文/黄相锦
1 引言
在工业4.0迅猛发展的大趋势下,机械臂越来越广泛地被应用在工厂、实验室、医疗等智能环境中。由于能够执行运输各种零件、试验原料、医疗物品等的任务,代替工人进行体力劳动,因此机械臂能大幅提升应用领域的自动化水平。其中,机械臂的轨迹规划作为对机械臂进行导航的关键技术,直接决定了机械臂完成运输任务的质量。
在上述应用中,将机械臂应用于无损诊断与检测、微损精确定位操作、外科手术规划与模拟、新型手术医疗方法等中,不仅促进了传统医学的进步,也带动了新技术、新理论的发展。
2 机械臂轨迹规划总述
机械臂需要对操作步骤进行设定来完成任务目标,而轨迹规划与设定操作步骤有着紧密的联系。由此,机械臂的正常运转依赖于轨迹规划,对机械臂进行合理的轨迹规划会对机械臂的运转过程以及作业效率产生至关重要的影响。
机械臂的轨迹是指,在运动过程中,其末端的位移、速度以及加速度。轨迹规划是指,基于运动学原理在笛卡尔空间中和关节坐标空间中根据目标要求计算出预期的运动轨迹。在机械臂的整体设计规划中,轨迹规划是底层规划。

图1:医疗机械臂关节示意图
一般而言,在对两个预定的端点之间的轨迹进行规划时,能够得到多条不同的轨迹。例如,机械臂既能够沿将起始位置和终点位置相连的直线进行运动,也能够在光滑的圆弧形轨迹上进行运动。
既可以在关节坐标空间中进行轨迹规划,也可以在笛卡尔空间中进行轨迹规划。但是,无论哪种轨迹规划方式都需要得到连续且平滑的运动轨迹。
基于笛卡尔空间的轨迹规划,是将执行器的位置和姿态、速度、加速度等表示为时间的函数,而对应的关节位置、速度及加速度等由执行器的时间函数导出。笛卡尔空间的轨迹规划具有直观性强,规划的路径符合度较高,容易实现连续路径控制的特点。但是,由于机械臂的运动驱动需要在关节空间这一级中实现,因此笛卡尔空间的规划需要通过逆运动学矩阵和逆雅可比矩阵将规划的结果映射到关节空间,运算量大;并且,在映射中还可能产生奇异点和反解的非一致性等问题。此外,由于传感器对各关节构件在欧氏空间中的精确位姿进行定位较为困难,因此对于实时控制机械臂而言是很大的挑战。
基于关节空间的轨迹规划,是将关节变量表示为时间的函数来描述操作臂预期的运动。规划得到的轨迹能直接作为驱动给定指令,无需在笛卡尔空间坐标系中对两个路径点之间的路径形状进行描述,具有计算量小、效率高、实时性好的优点;另一方面,基于关节空间的轨迹规划只受关节速度和加速度的限制,并且,关节空间与直角坐标空间之间的映射关系并不连续,因此并不存在奇异性等问题。
本文将在关节空间探讨对医疗机械臂进行轨迹规划的方法,研究如何确保速度和加速的连续性,保证关节较小冲击及机械臂平稳运行和精确定位。
3 医疗机械臂模型设计
在对用于医疗领域的机械臂进行设计时,为使其到达一定空间范围内的任意位置,机械臂一般应具有3个自由度,由P(移动关节)与R(旋转关节)组合而成。另一方面,为了模仿人手并实现医疗机械臂的末端能够调整至任意的姿态,通常需要6个主动自由度的医疗机械臂完成位置和姿态的确定。本文提出的医疗机械臂模型如图1所示。
4 多项式插值算法
4.1 轨迹规划指标
在对机械臂进行轨迹规划时,有若干反映轨迹规划曲线特性的参数,对于机械臂的轨迹规划过程以及机械臂的运动学及动力学特性的有重要的影响,分析这些参数具有重要的意义。这些参数主要包括最大速度、最大加速度以及最大冲击等。
为了实现平稳的机械臂定位过程,在进行运动规划时,除了需要确保位置和速度的连续性,在此基础上,还需要保证加速度不出现突变,以避免在末端产生振动、即所谓的抖振现象。各个关节的约束如下:

表1:路径点的参数

式中,t0表示运动的起始时间,tf表示运动的终止时间,θ0表示起始点的关节角,θf表示终止点的关节角,表示起始点的关节角速度,表示终止点的关节角速度,表示起始点的关节角加速度,表示终止点的关节角加速度。
通常,需要对关节运动进行规划,以控制机械臂的关节空间运动量,从而确保平滑的关节运动轨迹和平稳的运动。其主要内容包括关节运动轨迹的选择和关节运动位置的插值。如图2所示,某关节在t0时刻的关节位置为θ0,在tf时刻位置为θf。
关节的运动轨迹可以有很多条,如图2示出的轨迹1~3,按轨迹1和轨迹2运动,机械臂运动过程中会有波动,这是不希望的。按轨迹3运行,则机械臂能够平稳的由初始位置到达目标位置。因此,通常选择类似轨迹3的轨迹,经过插值后控制机械臂的运动。
4.2 三次多项式插值
考虑某关节从t0时刻的关节位置θ0运动到tf时刻的关节位置θf,假设这两个时刻的速度均为零,可以得到机械臂关节运动的边界条件,如下式(4)。

令关节位置位置为式(5)所示的三次多项式,对其求一阶导得到式(6)所示的关节速度多项式。
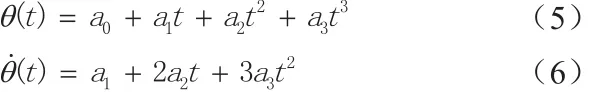
将边界条件式(4)代入式(5)和式(6),求解出系数a0-a3,将系数代入式(5)和(6)中,得到如式(7)所示的三次多项式插值的关节位置表达式以及如式(8)所示的关节速度表达式。

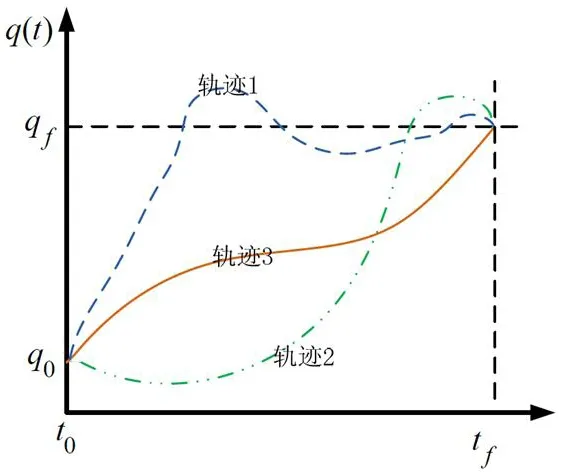
图2:关节的轨迹规划
然而,三次多项式插值方法只适用于起始点和终止点的速度为零的运动情况。一般情况下,运动轨迹在中间多个点有位姿要求,规划的轨迹需要过路径点。如果在每个通过的路径点都进行停留,则三次多项式插值方法完全适用。
4.3 五次多项式插值
但是,对于医疗领域,通常要求机械臂在运转过程中不做任何停留以提高作业效率。另外,对于尤其是精密医疗外科手术这样的应用场景,要求避免机械臂因加速度突变引起的抖振现象,三次多项式插值算法并不能满足要求。
对于本文涉及的医疗机械臂而言,考虑到机械臂运行的环境中没有物体的遮挡,对空间轨迹没有太高的要求,另一方面,要在保证关节速度、加速度连续的同时避免关节较大的冲击。因此对应用于医疗领域的机械臂提出采用五次多项式插值算法。
通过采用高阶多项式插值方法将机械臂关节空间的起始点与目标点的加速度的参数考虑在内。在该情况下,机械臂关节运动的边界条件如下:

满足上述条件的多项式插值函数需要6个系数,因此选择五次多项式函数作为各关节轨迹的插值函数,其形式如式(10)所示。

对于五次多项式插值,不仅能实现运动过程的冲击最小化,而且相应的速度函数为相对于时间变量的四次函数,加速度函数为相对于时间变量的三次函数,能够得到连续的速度曲线和加速度曲线,并且上述曲线具有较好的平滑性。

图3:三次和五次插值的关节位置对比

图4:三次和五次插值的关节速度对比
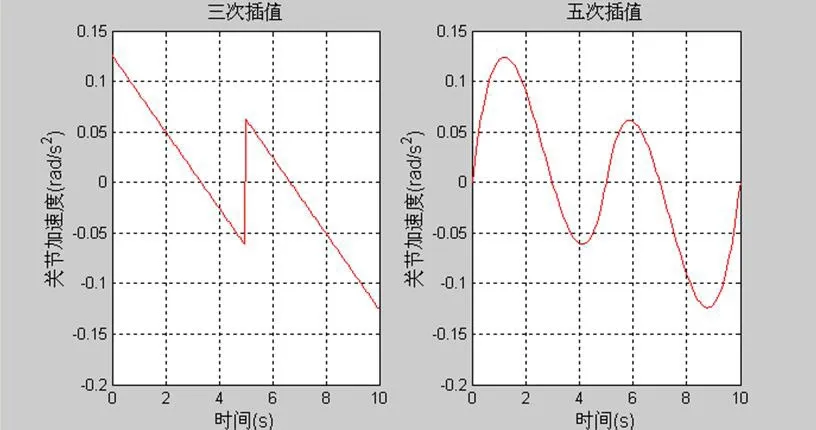
图5:三次和五次插值的关节加速度对比
其中,在运动过程中,关节速度和加速度为:

最终得到:

5 插值算法的仿真
针对机械臂中的某一旋转关节,使该关节依次通过如表1所示的三个点,其中,采样周期为0.05s。在matlab中对过路径点的三次多项式插值算法和五次多项式插值算法分别进行仿真。如图3~图5示出仿真得到的关节位置、速度和加速度。
从仿真结果可以看出,三次多项式插值算法能够保证各个点的关节角、角速度的连续性,但角加速度出现了突变。另一方面,五次多项式插值算法确保了加速度的连续性。因此在关节空间规划算法中,通过采用五次多项式插值,并在规划中合理地选取中间点,就能够限制最大加速度、速度等,从而实现对运动平稳性的控制。
6 结语
本文探讨了实现加速度平滑过渡的医疗机械臂轨迹规划方法。通过在关节空间对医疗机械臂采用五次多项式插值算法进行轨迹规划,确保速度和加速的连续性,保证关节较小冲击及医疗机械臂平稳运行和精确定位。并且,在关节空间内对过路径点的三次多项式插值算法和五次多项式插值算法进行了仿真分析,结果表明,五次多项式插值算法不仅能确保速度、加速度的连续,同时也保证关节冲击在较小的范围内。证明五次多项式插值能够满足尤其是精密医疗外科手术这样的应用场景中的要求,避免医疗机械臂因加速度突变引起的抖振现象。
