基于小波变换的图像处理技术

文/赵满庆

小波变换处理技术概念是由上个世纪八十年代英国学者J.Morlt提出的。在十几年后，数学家Y.myer构造出了一种真正可实际操作的小波处理技术。后来美国数学家和电子学家S.Mallat也参与到小波技术开发研究中，二者共同构造出了小波基的立体结构分析理论。目前小波变换图像处理技术已经广泛应用于频道信号分析、地质勘测图像处理、算子理论分析、图像增强技术处理、故障诊断等多个领域，其中以图像处理应用最为广泛。

1　小波变换技术种类分析

相比较传统的Fourier变换、加里傅里叶变换、小波变换属于实时频域变换，在时频特殊化定位和图像多频分辨能力上具有特殊优势。小波变换可以更快速的将信号处理信息和图像包含信息快速提取出来，其整体形状大小不变，但是局部可以进一步延伸分析。

1.1　连续小波变换技术分析

传统的加里傅里叶变换（STFT）其窗口函数为：

在公式中∂是频率限制参数，可以通过测量直接获取，t为固定时间参数，ω为信号固定波段数。e-it为信号输出频率。公式主要是通过对函数内部双轴即：时间轴和频率轴的播放限制技术而得到的，得到的频域分析处理窗口大小具有固定性。时频窗口必须具有可调性，即要求变换技术需可以在图像高频部分具有良好的时间分辨率，而在图像信号的低频部分，可以由良好的频率分辨率。所以在传统函数的基础上添加窗口函数：

其中a和b代表两个波段的数据参数，参数选定必须选择平行波段。t为固定时间参数，β为区域窗口字符代码。显然，在实际应用中，窗口函数并不能保证所用小波变换值均有意义，尤其在对高频域信号处理和图像处理应用中，这种小波变换只能做到简化问题，并不能做到直接处理问题，其应用目的，只是对原问题的简化求解，所以必须保证连续小波变换后还可以进行逆变换。同时作为窗口函数，为了保证时间窗口和频率窗口在时间上具备相同的时间衰减性，需要函数具备以下性质：

1.2　离散小波变换技术分析

在对许多图像数字信号处理时必须进行离散化处理。也就是将离散小波变换的指针通过尺度测量，根据数据结果参数a、平移参数b进行离散化处理。常用的处理方式是利用网络算法中的二进制动态采样算法，对每个网络点进行数据结算。想要进一步观看信号的更精细数字信号，可以继续放大倍数，所以在相关研究领域，小波离散变换也被称为图像信号数学显微镜。

2　小波变换在图像处理中的实际应用分析

小波变换处理是传统傅里叶变换的集成和升级，具有多分辨率分析和良好的视频性特点。在对高频数字信号进行变换处理时，通过逐渐拉抻精细时间步长，可以对分析对象任意细节进行聚焦分析。因此十分适合对图像或视频信号这类波动幅度大，跳跃性强的信号进行变换处理，所以在相关领域具有广泛应用。

2.1　基于小波变换的图像压缩

基于小波变换技术的二维小波分析的图像压缩方式有许多种，常用的主要有小波包、小波灵活变换压缩、小波矢量变换压缩等。二维小波分析是小波变换技术应用的重要方面。在对目标图像进行小波分解时，可以得出一整套子图像信号，具体理解为一个二维离散型图像{c（m,n）}。每个子图像的目标分辨率都不相同，小波变换技术将图像各层分辨率分解为一个近似值A1，水平细节分量为cH1，垂直分量为cV1，细节分量为cD1。具体分解过程如图1所示。

不同分辨率的字图像可以对应不同的图像频率，高分辨率对应高频，反之低分辨率对应低频。对处理图像而言，其最主要的数字显示就是低频部分，所以最简单的压缩办法就是利用小波变换技术分解到高频部分，只留低频部分。

2.2　基于小波变换的图像去噪

小波变换技术还可以用于对图像的去噪处理，首先需要对目标图像进行二维信号的小波分解，体现设定小波分解层次选择一个小波固定数值N，然后计算各分阶层到N的计算信号。最后根据小波对图像分解后得出的低频系数，以及之前计算过得各层阈值，进行二维小波重组，整个操作的重点是阈值选取和阈值量化。

3　实验研究

表1：图像测试表

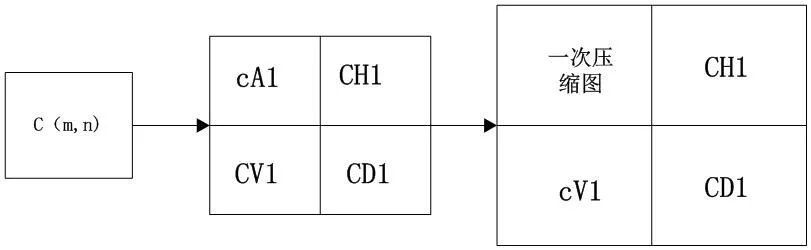
图1：图像压缩示意图

为了探寻小波变换在图像处理中的实际应用，用report('jimm')对jimm_org.png真彩图像文件计算阈值分别为0，5，10和20的情况下进行3级非标准haar小波变换和重构后，系数为“0"的数目和以PNG格式存储的重构图像文件大小，实验结果得到图像测试表如表1所示。

根据实验从图像测试表和观察不同阈值下的重构图像可得出以下结论：

（1）可利用小波变换与重构对图像文件进行压缩；

（2）通常在给定小波基函数条件下，阀值越大，系数为0的数目就越多，重构图像文件压缩率也越高，重构的图像失真程度随之增加。

（3）阀值＞0时，利用小波变换与重构进行图像压缩是一种有损压缩方法，可以根据实际需要在图像失真度允许的范围内选择适当的阀值来确定压缩率。

4　结束语

根据小波变换在图像处理上主要应用中，可以肯定小波变换在对图像压缩时，可以提高压缩比例，加快压缩速度，在压缩后，可以保证图像主要数据不变，呈现的基本图形和原图一致。而基于小波变换的图像去噪技术，可以提高图像清晰度，根据使用者需求改变图像呈现方式。由此可以看出，小波变换技术在图像处理方面具有重要优势，已经成为国际上公认的最强技术，在与图像数据充分结合的基础上，将图像处理工作提高到新的层次。