基于正交化方法的回归分析
2018-07-14胡良平
胡良平
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029
1 概 述
1.1 何为基于正交化方法的回归分析
基于正交化方法的回归分析是在构建多重线性回归模型时,先对数据进行“Gentleman-Givens 变换”[1-2],但仍基于“线性最小二乘原理”推导出的公式估计回归系数。
1.2 基于正交化方法的回归分析应用的场合
当拟做多重线性回归分析的原始数据存在严重的“病态”时,采用此方法构建多重线性回归模型,可以最大限度地消除“病态数据”对建模结果造成的影响。
1.3 基于正交化方法的回归分析的原理
此法使用“Gentleman-Givens变换”[3]校正数据,并且在计算数据矩阵的QR分解[4]的上三角矩阵R时十分谨慎。相对于其他正交化方法(例如Householder变换[3]),此法的优点是不需要将数据矩阵存储在计算机的内存中。
2 基于正交化方法的回归分析解决实际问题
2.1 此法可否解决多重共线性问题
2.1.1问题与数据结构
沿用文献[5]中的“问题与数据”,并基于派生变量得到的“最优回归模型”所决定的“数据集”,来提出下面的“新问题”:即“weight”的回归系数为“-88.00801”,这个“负值”表明:体重越重的人收缩压(SBP)越低,这似乎不符合临床专业知识。尽管计算出来的因变量的预测值在专业上都成立,而且模型的残差方差=122.32418、R2= 0.9931,这些结果都提示所构建的多重线性回归模型很好。但毕竟存在回归系数的正负号不符合专业知识的“严重瑕疵”,这是一个需要彻底解决的“疑难问题”!
2.1.2所需要的SAS程序
尝试采用“基于正交化方法”解决上述提及的“疑难问题”。所需要的SAS程序如下:
data a1;
input id age height weight bmi sbp;
cards;
(此处输入文献[5]表1中50行6列数据)
;
run;
/* 以上程序为了创建数据集a1 */
data a2;
set a1;
x1=age*age; x2=age*height; x3=age*weight;
x4=age*bmi; x5=height*height; x6=height*weight;
x7=height*bmi; x8=weight*weight; x9=weight*bmi;
x10=bmi*bmi;
run;
/* 以上程序是在数据集a1基础上创建数据集a2,它增添了10个派生变量 */
proc reg data=a2;
model sbp=age weight x3 x6-x10/noint;
quit;
/* 以上程序是调用REG过程并基于数据集a2拟合文献[5]中那个“最佳”回归模型 */
proc orthoreg data=a2;
model sbp=age weight x3 x6-x10/noint;
quit;
/* 以上程序是调用ORTHOREG过程并基于数据集a2拟合文献[5]中那个“最佳”回归模型 */
【SAS程序说明】在以上的SAS程序中,都用“/* ……… */”注释语句作了说明。
2.1.3SAS输出结果及其解释
以上第1个SAS过程步(REG过程)程序的主要输出结果如下:

参数估计值
以上第2个SAS过程步(ORTHOREG过程)程序的主要输出结果如下:

变量自由度参数估计值标准误差t值Pr > |t|age11.821817155899260.49294033783.700.0006weight1-88.008006763805126.676358039-3.300.0020x31-0.00970853699460.0034186421-2.840.0069x610.645688011242420.19305159293.340.0017x714.324558948331461.30917299623.300.0020x81-0.058353118670680.01883696-3.100.0035x910.785296033542440.25836051573.040.0041x101-2.62458498623560.8771470203-2.990.0046
比较上述由“REG过程”与“ORTHOREG过程”对同一个具有严重共线性问题的资料进行多重回归分析的结果可知:后者比前者所估计的“参数值”更精细,但仍没有消除多重共线性对回归系数的严重影响(尤其是weight前的回归系数为负值且其绝对值还比较大,不符合临床专业知识)。也就是说:SAS/STAT中的“ORTHOREG过程”并不能解决“多重共线性问题”。
2.2 此法可否解决高阶多项式曲线拟合问题
2.2.1问题与数据结构
假定有一个高阶多项式资料,见表1。
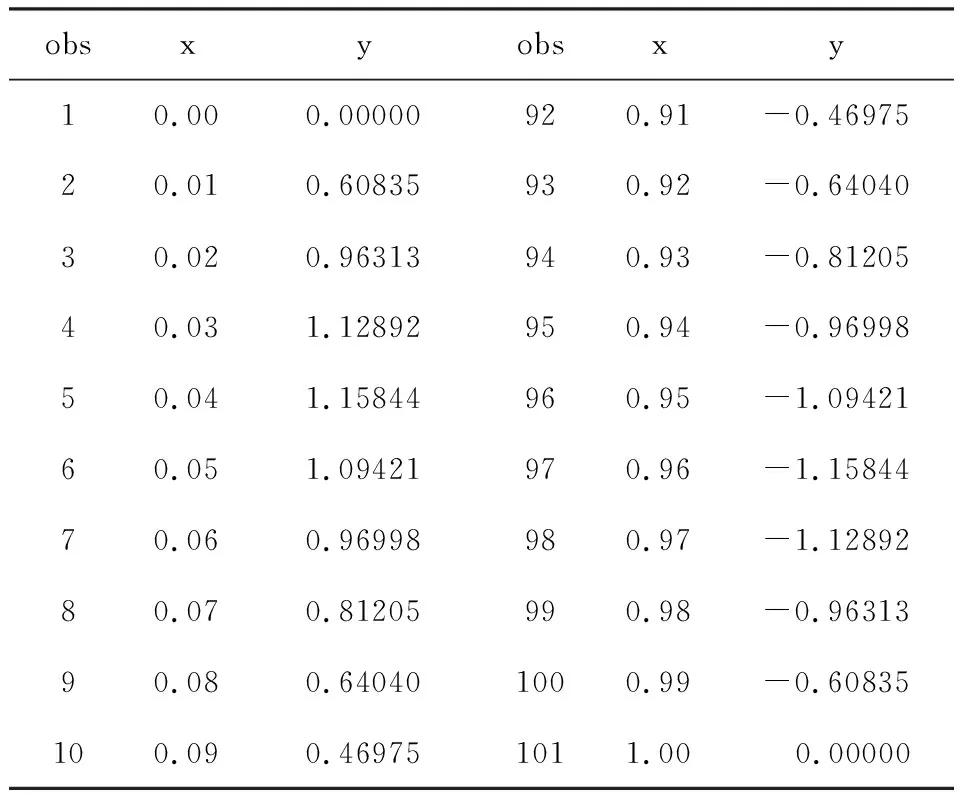
表1 某资料中首尾各10对数据(n=101)
注:表1中省略编号为11到91的数据
绘出表1资料中(x,y)各点的散布图,见图1。
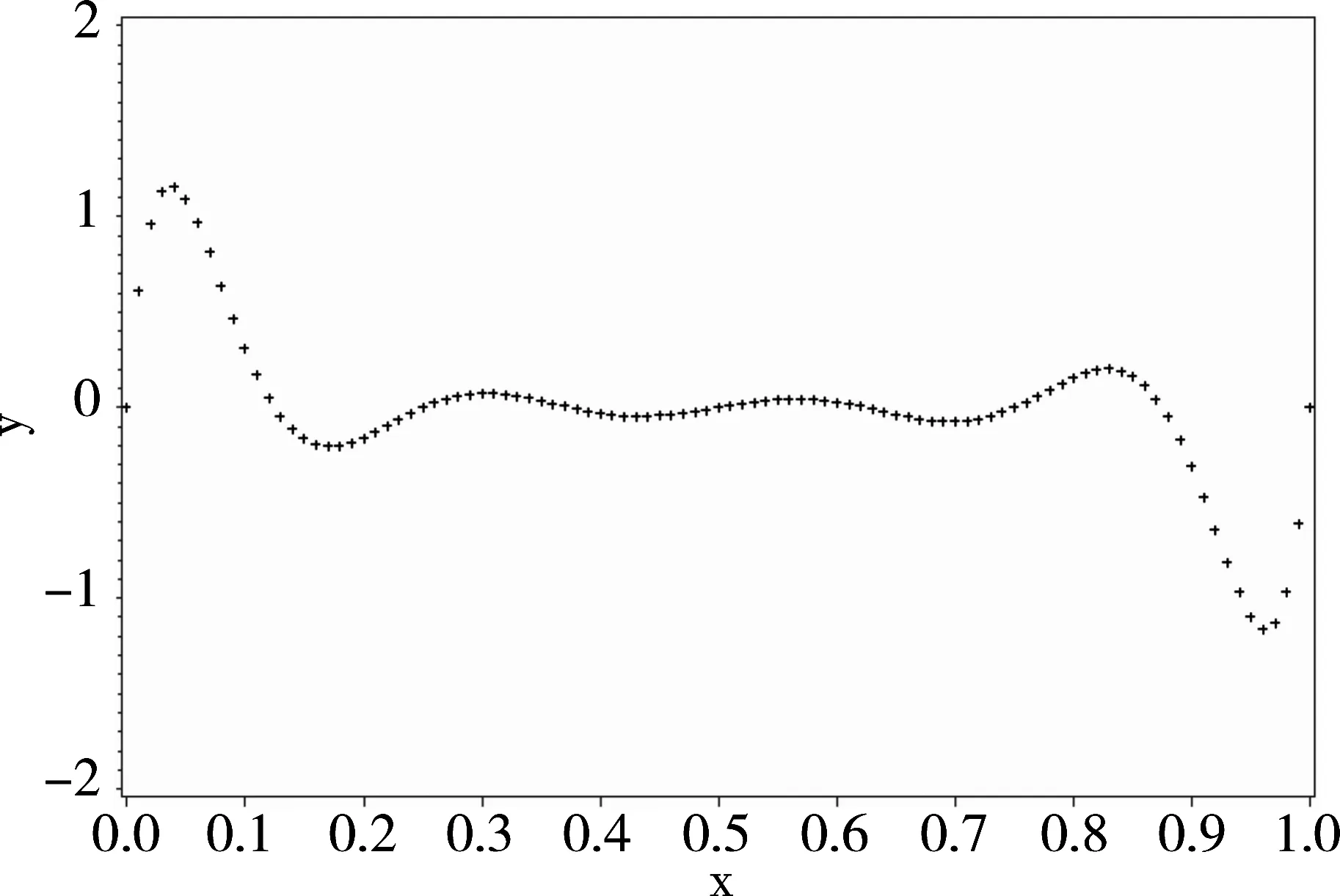
图1 表1资料中(x,y)散布图
【问题】试拟合图1中y依赖x变化的回归模型。
2.2.2所需要的SAS程序
data Polynomial;
do i=1 to 101;
x=(i-1)/(101-1);
y=10**(9/2);
do j=0 to 8;
y=y * (x - j/8);
end;
output;
end;
run;
/* 以上程序是为了产生表1中的全部101对数据 */
proc gplot data=Polynomial;
plot y*x;
run;
/* 以上程序是为了绘制图1中的散布图 */
proc glm data=Polynomial;
model y=x|x|x|x|x|x|x|x|x;
run;
/* 以上程序是为了调用GLM过程拟合九次多项式曲线回归模型 */
ods graphics on;
proc orthoreg data=Polynomial;
effect xMod=polynomial(x / degree=9);
model y=xMod;
effectplot fit / obs;
store OStore;
run;
ods graphics off;
/* 以上程序是为了调用ORTHOREG过程拟合九次多项式曲线回归模型并绘图 */
2.2.3SAS输出结果及其解释
以下是“GLM过程步”输出的计算结果:

参数估计值标准误差t值Pr > |t|截距0.448960.1254793.580.0006x24.610626.0548524.060.0001x*x-443.7403493.388508-4.75<0.0001x*x*x2626.90806B642.9727184.09<0.0001x*x*x*x-7371.23677B2327.022377-3.170.0021x*x*x*x*x10697.73145B4741.5988972.260.0264x*x*x*x*x*x-7749.24904B5468.101939-1.420.1598x*x*x*x*x*x*x2214.08419B3328.3556610.670.5076x*x*x*x*x*x*x*x-0.00610B830.439899-0.001.0000x*x*x*x*x*x*x*x*x0.00000B---
以上结果表明:用GLM拟合多项式曲线回归模型并不太合适,其中,标志“B”的那些行上的参数估计值不准确。
以下是基于GLM过程拟合结果绘制出的曲线图,见图2。
图2中的实线是基于GLM过程计算的结果,而圆圈是实际观测到的结果。不难看出,拟合效果很不理想。
以下是“ORTHOREG过程步”输出的计算结果:
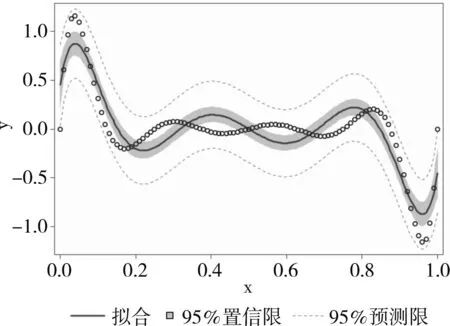
图2 基于GLM过程拟合结果绘制出的曲线图

参数自由度参数估计值标准误差t值Pr > |t|Intercept1-2.17224978239E-115.841067E-12-3.720.0003x175.99773124392843.526134E-102.16E11<0.0001x^21-1652.407813618026.8407273E-9-242E9<0.0001x^3114249.45397693735.9828349E-82.38E11<0.0001x^41-64932.46157501272.8072627E-7-231E9<0.0001x^51173315.3593603037.6781594E-72.26E11<0.0001x^61-280158.0364593531.2614251E-6-222E9<0.0001x^71269781.8128871421.2252919E-62.2E11<0.0001x^81-142302.4947098696.4807927E-7-22E10<0.0001x^9131622.77660222611.4379253E-72.2E11<0.0001
以上结果表明:拟合的九次多项式曲线回归模型中各参数均具有统计学意义。
以下是基于ORTHOREG过程拟合结果绘制出的曲线图,见图3。
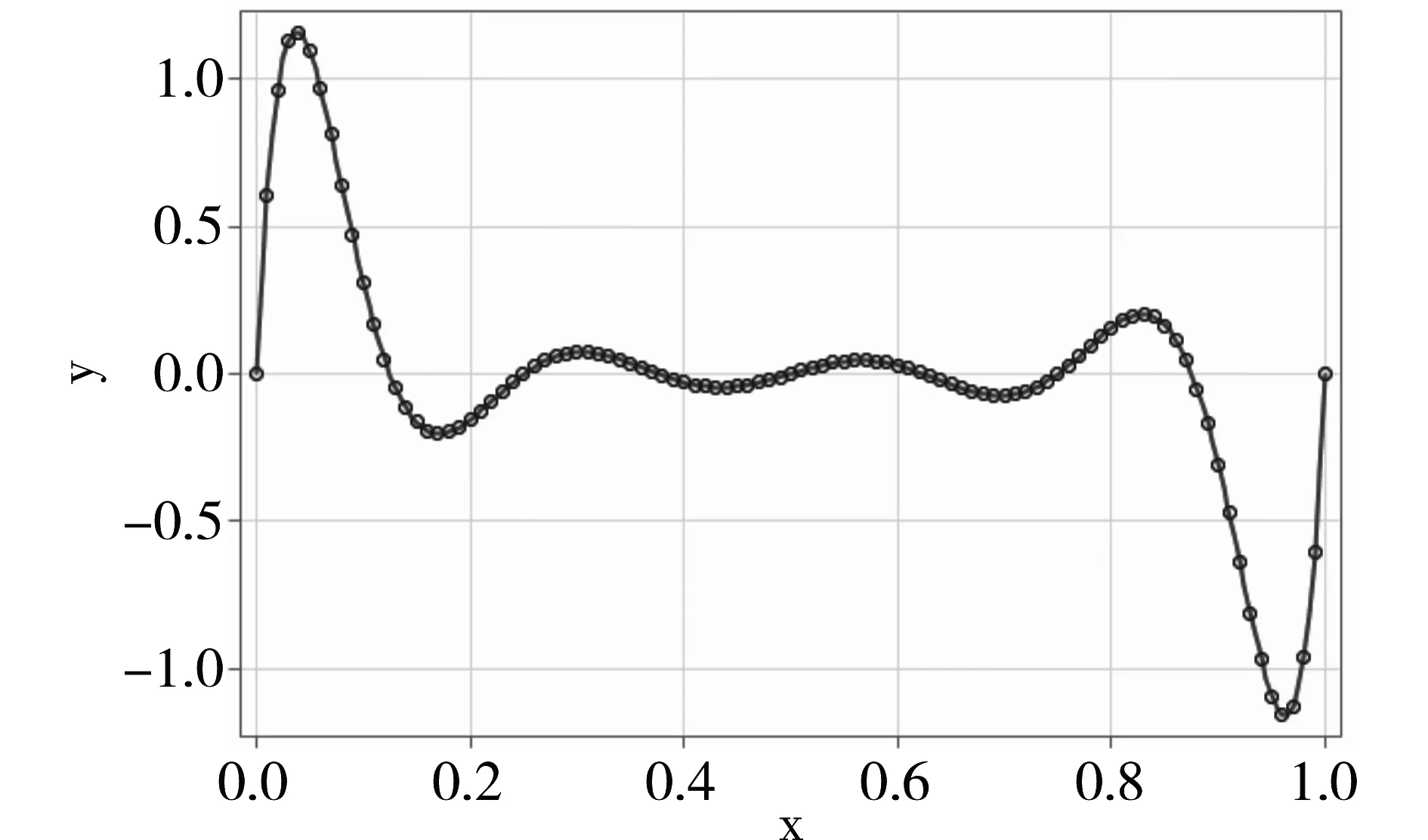
图3 基于ORTHOREG过程拟合结果绘制出的曲线图
图3中的实线是基于ORTHOREG过程计算的结果,而圆圈是实际观测到的结果。不难看出,拟合效果非常好。
【说明】本例表1中的资料属于一种相当严重的“病态”资料,由图3可知,当x在(0.00,0.18)之间变化时,y的变化形成了一个“尖峰”;当x在(0.18,0.82)之间变化时,y的变化形成了近似平行于x轴的一条“略有起伏的波浪线”;而当x在(0.82,1.00)之间变化时,y的变化形成了一个“低谷”。
