反九点井网非活塞式水驱面积波及系数计算方法

2018-07-13周海燕石洪福王记俊

复杂油气藏 2018年2期

孙　强，周海燕，胡　勇，石洪福，王记俊

(中海石油(中国)有限公司天津分公司，天津 300452)

渤海油田普通稠油油藏分布广泛，大多采用面积井网开发。稠油粘度高，渗流阻力大，渗流规律偏离达西定律[1]，只有当驱动压力梯度超过启动压力梯度时，稠油才能流动。因此，在评价普通稠油油藏水驱开发效果时须考虑非达西渗流特征。且稠油油藏流度比高，水驱时存在强非活塞性的特征，不能简单地简化为单相流体处理。

面积波及系数是研究不同注采井网条件下原油采收率的重要依据，因此如何准确计算水驱面积波及系数对评价普通稠油油藏水驱开发效果至关重要。目前国内外许多学者已经对面积波及系数进行过相应的研究。张丽华、范江等分别从实验、数值模拟、概率论、量纲分析等角度对水驱面积波及系数进行了研究[2-8]，但未在数学理论上解决面积波及系数的计算问题。计秉玉、唐海、郭粉转等运用流管法对不同井网形式下的面积波及系数进行了推导[9-21]，但是研究的油藏流体均为稀油，计算渗流阻力时按单相处理，并未考虑油水两相非活塞性，不适用于油水粘度比较高的普通稠油油藏。

本文基于流管法和油水两相非活塞式水驱油理论，建立了一套考虑稠油启动压力梯度下反九点井网面积波及系数的计算方法，并分析了稠油启动压力梯度、注采井距、注采压差对油藏面积波及系数的影响。

1　模型建立

1.1　反九点井网油藏模型

反九点井网中一个注采井组可以划分为16个三角形渗流单元，分为边井单元和角井单元，如图1所示。图1中OBC为边井单元，OAC为角井单元，OC是两个注采单元的公共流线，C为AB的中点。

图1反九点井网示意

模型具有以下假设条件：①生产井和注水井间压差恒定；②刚性多孔介质，流体不可压缩；③非活塞式水驱油，存在油水两相区；④考虑稠油启动压力梯度。

1.2　拟流管长度与截面积

对于任意一个三角形渗流单元，可剖分为m根流管，如图2所示。在三角形渗流单元△MIP中，I为注水井，P为生产井，每根拟流管存在一个拐点D，∠MIP为α，∠MPI为β，∠DIP为α0，∠DPI为β0，且满足：

(1)

根据几何关系，注水井I到拐点D之间的长度L1为：

(2)

从注水井I到生产井P间的任意一条拟流管的长度L2为：

(3)

图2流管剖分示意

在流管上任意点ξ处，流管的截面积为：

(4)

式中，h为地层厚度；ξ为流管中线任意点距注水井的距离；rw为井筒半径；d为注采井距；△α为流管中注水井角增量；△β为流管中生产井角增量。

1.3　流量方程推导

室内实验表明普通稠油油藏存在启动压力梯度，油相流量方程不再符合线性达西定律[22]：

(5)

式中：qo为油相流量；μo为油相黏度；kro为油相相对渗透率；k为储层渗透率；ξ为从注水井出发的拟流管的中线长度；A(ξ)为拟流管在ξ处的横截面面积；Go为稠油启动压力梯度。

水相流量方程：

(6)

式中：qw为水相流量；μw为水相黏度；krw为水相相对渗透率。

其中启动压力梯度表达式为[1]：

(7)

由式(5)和式(6)求和并积分得任一拟流管见水前油水两相区的压降：

(8)

式中：qt为流体总流量。

由式(5)积分得任一拟流管中纯油区的压降：

(9)

式中：Swc为束缚水饱和度；ξf为流管中线水驱前缘处距注水井的距离。

拟流管中两端压差为：

Δp=Δp1+Δp2

(10)

根据式(8)、(9)、(10)，联立可得拟流管见水前的流量表达式：

(11)

拟流管中渗流阻力表达式：

(12)

油水两相区中稠油启动压力梯度造成的附加压降：

(13)

纯油区中稠油启动压力梯度造成的附加压降：

ΔpG2=Go(L2-ξf)

(14)

由式(11)可以看出，考虑启动压力梯度后，在油水两相区和纯油区分别存在一个启动压力梯度造成的附加压降，如式(13)和式(14)所示。当注采压差能够克服附加压降时，注入水才能形成有效驱替。在水驱普通稠油的过程中，随着油水两相区逐渐扩大，纯油区逐渐减小，渗流阻力不断变化，同时由启动压力梯度造成的附加压降也不断变化。

1.4　水驱前缘位置确定

在油水两相区，任一位置ξ处的饱和度和水驱前缘位置ξf可以通过式(15)确定：

(15)

式中：φ为地层孔隙度；Sw为含水饱和度；fw′(Sw)为任意含水饱和度对应的含水变化率。

假定某流管中油水前缘到达拐点D时间为t1，到达生产井P点时间为t2。

由式(4)和式(15)联立可得到不同时刻的油水前缘位置。

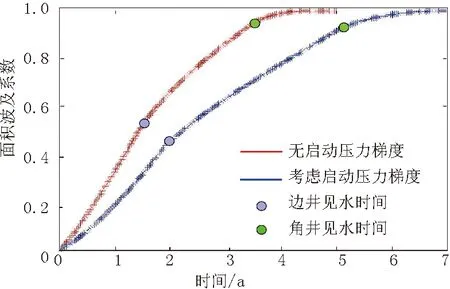
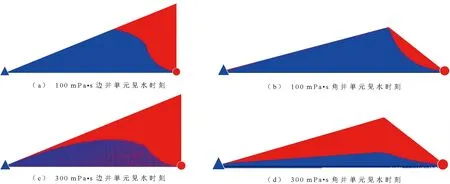
当t

(16)

式中：Swf为前缘含水饱和度。

当t1

(17)

1.5　水驱面积波及系数计算

不同时间下，注采单元△MIP中各流管内水驱前缘推进的位置不同，可以求得不同流管内的水驱波及面积。

当时t

(18)

式中：ξfi为第i根流管中水驱前缘距注水井的距离。

当t1

(19)

式中：L1i为第i根流管中注水井到拐点之间的距离；L2i为第i根流管中注水井到生产井之间的距离。

当t>t2时，第i根流管的水驱波及面积为：

(20)

根据每根流管的水驱波及面积Si，进而得到不同时刻计算单元的面积波及系数：

(21)

式中：SΔMIP为三角形渗流单元△MIP的面积。

2　模型求解

根据所建立的流管模型，以时间微元△t为步长，通过迭代计算可以求解不同时刻井网的面积波及系数。求解程序框图如图3所示。

图3反九点井网面积波及系数求解框图

将上述建立的三角形流管模型应用到反九点井网。由前述可知，反九点井网分为边井单元和角井单元，根据反九点井网面积波及系数求解框图可以计算得到面积波及系数的变化趋势。由图4可以看出，稠油启动压力梯度对面积波及系数的影响较大，当模型中考虑稠油启动压力梯度后，水驱面积波及系数变低。

图4启动压力梯度对面积波及系数的影响

由于边井和角井的存在，面积波及系数随时间的变化趋势整体表现为：初期增加较快，随着边井和角井依次见水，面积波及系数增加速度逐渐减缓，如图4所示。因此，应采用合理的开发方案延长油井的无水采油期。且边井和角井应该采取不同的工作制度，以使注入水驱替得更加均匀。

3　实例分析

依据上述模型，参考渤海某稠油油田数据，确定模型的输入参数为：储层渗透率1 500 ×10-3μm2，注采井距350 m，地层水粘度0.7 mPa·s，孔隙度0.25，油层厚度10 m。在该模型的基础上，对原油粘度、注采压差和注采井距进行了敏感性分析，分析了各参数对面积波及系数的影响。

3.1　原油粘度

注采压差为15 MPa，研究原油粘度分别为50，100，150，200，250，300 mPa·s时启动压力梯度对反九点井网面积波及系数的影响。其中，由式(7)可得三种原油粘度下启动压力梯度分别为0.006，0.012，0.017，0.021，0.026，0.030 MPa/m。

原油粘度越高，边井和角井的见水时间越晚，相同注入时间下水驱面积波及系数越低，如图5所示。这主要是因为随着启动压力梯度的增加，水驱过程中需要克服其产生的附加阻力越大，从而造成驱替速度越慢，水驱波及程度越低，形成的死油区越大，如图6所示。且当启动压力梯度过大时，注采压差不足以克服其产生的附加阻力，则注水井与生产井之间无法建立有效的驱替系统，导致“注不进，采不出”的现象。