基于BP神经网络的国家稳定性研究

李平舟，赵朗程

（北京邮电大学 国际学院，北京　100876）

0　引言

如何评判国家的稳定性一直以来都是各类政治、经济机构研究的重点。现有评价体系中脆弱国家指数（Fragile State Index，FSI）是最广为认可的指标。脆弱国家指数是世界上178个国家面对不同压力时所表现出的脆弱程度排名[1]。该指数由和平基金会专有的冲突评估系统（CAST）分析得出，CAST采用综合社会学方法论，主要使用定量评估，定性评估和专家验证三种方法来得出国家稳定性的指数。根据专业社会科学研究，每个被评估的国家具有12个政治，经济和社会三个方面的主指标以及超过100个子指标。CAST方法和FSI被广泛用于政治决策，社会分析以及发展研究[2]。

2009年 10月，联合国政府间气候变化专门委员会（IPCC）发表的《第五次评估报告》[3]与以往报告相比，强调了气候变化对国家社会经济和可持续发展方面的影响。而CAST方法中涉及气候变化的指标较少，难以分析气候变化对于国家的影响。

针对以上问题，本文采用BP(Back Propagation)神经网络的方法，根据CAST方法得出的脆弱国家指数，结合178个国家近几年以来的12项指标，其中2项为气候指标，训练得到气候变化和FSI之间的关系网络。

1　常用建模方法及评价

1.1　主成分分析法

主成分分析法（PCA），旨在利用降维的思想，将多个指标再划分为少数几个综合指标（即主成分），其中每个主成分都可以反映原始变量的大部分信息，且所含信息不重复[4]。

主成分分析法可消除指标间的相关影响，减少选取指标的工作量，并取累计贡献率高的主成分来代表原变量，减少计算工作量[5]。然而对于国家脆弱指数的评估而言，变量降维的过程会使得提取出的主成分带有一定的模糊性，从而失去实际意义和实际背景，使得抽象出的主成分难以有合理的解释。

1.2　层次分析法

层次分析法（AHP）是将复杂的多目标决策问题作为一个系统，将目标分解为多个目标或准则，进而分解为多指标的若干层次。通过定性指标模糊量化方法算出层次单排序和总排序作为多目标决策的系统方法[6]。

然而层次分析法缺少严格的数学论证和完整的定量方法，是一种带有模拟人脑的决策方法，包含较多定性色彩。而对于国家脆弱指数的评估需要大量的指标，数据统计量大且权重难以确定，层次分析法中的特征值和特征向量的维度较高，计算上相对困难。

1.3　模糊综合评价法

模糊综合评价法（FCE）是一种基于模糊数学的综合评价方法，通过指标分类及每个指标的等级评定建立评价标准集。在将每个指标分为多个等级后进行单因素模糊评价，构建评价矩阵 R。接下来将权重与评价矩阵进行合成，可得到评价事物的综合模糊评价隶属度，通过最大隶属度定级，得到最终的评价结果[7]。

模糊综合评价的评价结果为一个矢量而非点值，可以较为准确的刻画评价对象，然而评价国家脆弱性所需的大量指标，导致相对隶属度权系数偏小，权矢量与模糊矩阵R不匹配，结果会出现超模糊现象，无法分辨隶属度关系，甚至可能造成评判失败。

在实际建模中，还可将AHP与FCE建模方法相结合，即为AHP-模糊综合评价法。使用AHP建立递阶层次结构，确定指标体系，FCE用以对指标进行等级评价，确定目标等级。但过多人为因素干扰的根本问题并没有解决，模型主观性强，这将影响对国家脆弱性的客观评判。

为了客观评价国家的稳定与否，本文提出使用基于大量数据确定权值的 BP神经网络模型，计算输入指标与国家脆弱指数之间关系。

2　BP神经网络模型

2.1　BP神经网络的应用

国家稳定性评判的量化需要一个国家各方向的指标数据以体现其各项状态，从而结合各项指标，得到最终的评判结果。脆弱国家指数是现有的，基于专家智库各项定性、定量分析所得出的国家稳定性评价。其参考价值是巨大的，但由于缺乏与数据的直接联系，我们不能根据其结果分析一个国家某个特定方向上的发展状态。

为此我们引入BP神经网络的，BP神经网络是一种按误差反向传播（简称误差反传）训练的多层前馈网络[8]，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。通过训练网络得出某一指标与国家稳定性的直接关系，从而制定相应政策，指导国家发展。

BP神经网络的类型为有监督的学习，其样本包含以下两个部分：样本特征值和样本标签。样本特征值构成的样本特征集即为描述样本特征的描述子，在本文中，参考和平基金会评估国家脆弱指数的三个主要方面：政治，经济和社会，设定了10个指标。同时，为了表现气候变化对国家脆弱性的影响。本文参照柯本气候分类法，以气候和降水两个主要气候要素作为评估气候变化的指标。以上共计12个指标，作为描述某个国家特点的描述子。

样本标签表达一个样本的类别或取值。在本文中，国家脆弱指数即为样本标签。由于获取样本标签绝对真值非常困难，故本文参考和平基金会给出的FSI数据。FSI的值越大则表明国家脆弱性越高。

BP算法的输入为12个指标，输出即为表示国家稳定性的FSI。BP网络内两个重要的参数为权值和阈值，权值描述层与层神经元之间的关系，阈值描述神经元内联系。算法包括信号的前向传播和误差的反向传播两个过程，即计算误差输出时按输入到输出的方向进行，而调整阈值则从输出到输入的方向进行。正向传播时，输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号。若实际输出的脆弱国家指数与期望输出不相符，则转入误差的反向传播过程。误差反传是将输出误差通过隐含层向输入层逐层反传，并将误差分摊给各层所有单元，以从各层获得的误差信号作为调整各单元权值的依据。用过调整输入节点与隐层节点的联结强度和隐层节点与输出节点的联结强度以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数（权值和阈值），训练即告停止。此时经过训练的神经网即能对类似样本的输入信息，自行处理输出误差最小的经过非线性转换的FSI。

2.2　BP神经网络设置

本算法的基本原理是利用输出后的误差来估计输出层的直接前导层的误差，再利用这个误差来估计下一层的误差，如此循环，即可获得对所有层的误差估计[9]。

基本的BP神经网络包含三层网络结构：输入层，隐含层和输出层，各层节点之间无连接。这样，经过层层处理之后，可以得到输入向量与输出向量之间的非线性关系网络[8]。该网络的拓扑结构如图1所示.

图1　BP神经网络的拓扑结构Fig.1　Topology structure of BP neural network

样本输入数目为 k，输入向量为X，实际输出向量为Z，期望输出向量为T，输入层与隐含层连接权值为Wih，隐含层与输出层连接权值为Whi。网络具体学习步骤如下：

（1）初始化网络：为各个连接权值赋（-1，1）之间的随机数，设定误差函数e。

误差函数e为：

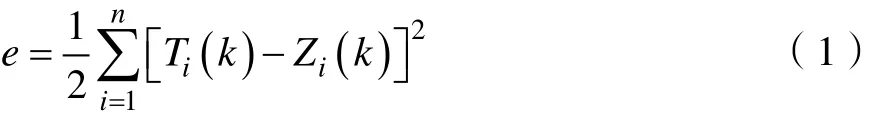
并设置计算精度和最大学习次数。

（2）随机选取第k个输入样本和期望输出，利用网络期望输入和实际输出，计算误差函数对输出层各节点的偏导数[9]。

（3）同理，可以根据隐含层到输出层连接权值，输出层和隐含层的输出计算误差函数来计算误差函数对隐含层各个节点的偏导数。

（4）利用输出层偏导和隐含层各个节点的输出来修正连接权值Wih，利用隐含层的偏导和输入层各个节点的输入修正连接权值Whi。

（5）计算全局误差，本文使用的全局误差函数为：

（6）检查网络误差，如果网络误差满足计算精度或学习次数大于最大学习次数，则结束算法。否则随机选取另一个不同学习样本再次进行训练[10]。

3　实验仿真

3.1　网络输入/输出设置

（1）样本输入设计：通过数据收集，共得到2000组样本数据，其中随机80%样本数据作为训练数据，余下20%样本数据作为检验数据以确保模型效果。

（2）网络设计：本文采用的学习优化算法为 Ada Grad[11]优化算法，网络输入为不同国家的12种指标值，设置隐含层节点150个，输出层节点1个，最大训练次数为 104次，学习率为 10–4，训练要求精度为 10–10，最小梯度要求为 10–10。

数据来源为[12]。我们使用80%的数据作为训练集，剩余20%用作测试集。

表1　网络的输入/输出Tab.1　Input/output of network

3.2　模型训练

实验平台：MacOS Sierra 10.12.6

Matlab R2015b;

CPU：Intel Core i5 4258U 2.4 GHz;

RAM：双通道8 GB

（1）训练过程

本次试验中，数据被随机分为训练数据，验证数据和测试数据，训练使用莱文贝格-马夸特算法，使用均方误差评估网络表现[13]。如图2所示，该模型在第13次迭代处达到最小均方误差，此时估计量与被估计量差值最小，拟合效果达到最优。确认检查值默认为6，在第11次迭代之后，样本误差呈上升趋势，故在第17次迭代时停止训练以保证不出现过拟合[14]。

此时均方误差为：5.31，梯度值为：40.3，Mu值为：0.1。此时生成误差-样本图。

（2）测试模型

测试结果如图3所示，该图为测试样本的验证结果，由图可知，绝大部分误差在0轴附近，少部分误差较大的点为样本本身特征的缺失导致信息不完全而判断失误，模型整体效果良好。该结果展示了国家脆弱性与输入指标之间的准确关系。

（3）对比分析

为验证将气候变化因素列入指标后对结果预测的准确性，本文使用除气候之外的10个指标采用相同网络进行试验。可以看出失去气候变化因素之后的预测，随样本数的增加，误差逐渐增高。加入气候因素的测试样本误差率为0.411%，而未加入气候因素的误差率则为1.982%误差率提高了约4.6倍。由此可见，加入气候因素，会对国家脆弱性的评估更为真实可信。

图2　网络训练Fig.2　Network training

图3　MSE误差曲线Fig.3　MSE error curve

图4　训练过程Fig.4　Training process

图5　训练结果Fig.5　Training results

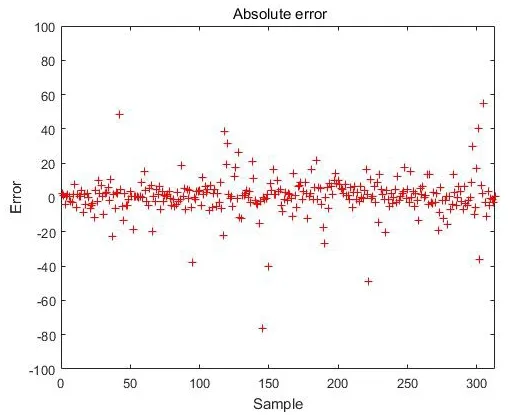
图6　测试误差Fig.6　Test error

图7　不考虑气候因素的测试误差Fig.7　Test error without considering climate factors

4　结论

气候变化要素是由联合国政府间气候变化专门委员会提出的一项影响国家稳定性的新指标。本文拟在美国和平基金会提出的评估国家脆弱指数的指标中加入气候变化因素，并使用 BP神经网络研究气候变化和原有指标对国家稳定性的共同影响。输入187个国家近十年的数据对网络进行训练，得出含气候变化在内的 12个指标与国家脆弱指数之间的非线性关系网络。相比于原有的不含气候指标的评估方法，有更好的预测效果，误差率降至0.411%。证明了气候变化会对国家脆弱性产生显著的影响。而事实上，气候变化也会对人口，教育等其他评估指标造成影响。后续工作将着重于研究气候变化如何其他评估指标造成影响，从而间接影响国家脆弱性。