城市物资配送路径寻优的算法比较

潘帅

摘 要：本文围绕物资运送至城市到达站后选择何种路线对配送点进行配送的问题展开讨论。首先，在平面直角坐标系中，确定配送点的位置坐标，然后通过建立最短巡回径路模型，设计遗传算法与蚁群算法分别对数值实例进行求解，得到最短巡回径路，最后比较这两种算法对寻求最短巡回径路问题的求解质量与收敛速度。

关键词：物资配送；平面直角坐标系；最短巡回径路；遗传算法；蚁群算法

中图分类号：O224；TP301.6 文献标识码：A 文章编号：1003-5168（2018）16-0127-04

Comparison of Algorithms for Optimizing Urban Material Distribution Path

PAN Shuai

Abstract： This paper focused on material transportation to choose what route to reach the station delivery point for distribution. First， in the plane right angle coordinate system， the location coordinates of the distribution point were determined， and then the shortest circuit path model was established. The genetic algorithm and the ant colony algorithm were designed to solve the numerical example， and the shortest path was obtained. Finally， the quality and convergence speed of the two algorithms for finding the shortest routing problem were compared.

Keywords： material distribution；planar rectangular coordinate system；shortest tour path；genetic algorithm；ant colony optimization

隨着国家产业结构调整的深化与电子商务的发展，我国货源结构发生了巨大变化。近年来，物资配送的市场份额逐年上升，究其根源，是电子产品、工业配件、食品、日用品等高附加价值的货物需求迅猛增加。以兰州为例，中铁快运股份有限公司的城市到达站有兰州站、兰州西站和中铁兰州物流中心等，所有到站货物进行分拨，配送至各配送点，如兰州西固营业部、兰州西站高铁营业部、兰州分公司和兰州站营业部等。

众所周知，地球是一个不规则的球体，将位于球面的形状显示在平面的显示器上就必然需要一个投影过程，投影之后的坐标（用X和Y描述）用于在平面上标识POI（POI是“Point of Interest”的缩写，中文可以翻译为“兴趣点”）[1]。在百度地图API中，通过经度（Longitude）与纬度（Latitude）描述地球上的某个位置，用BMap.MercatorProjection类来完成经纬度与平面坐标互相转换的计算。其中，经纬度的原点和平面坐标系的原点一致，即0°经线和地球赤道相交的位置[2]。本文是基于以上方法得出配送点相对于城市到达站的坐标。

1 配送车最短巡回路的问题描述

为了方便寻求最短配送径路，笔者对所研究问题作出以下假设：物资运送至城市到达站后，这批物资的体积重量小于等于1辆货车的标准载重，已知n个需要进行配送任务的配送点相对城市到达站的平面坐标为[xi，yi]，其中，[i=1，2，3，…，n]。此问题的目标函数：配送人员选择最短的巡回径路，降低运输成本，保证物资全部送到配送点处[2]。据此建立数学模型。

2 配送车最短巡回路问题的数学模型

2.1 货郎担问题

设有[n]个地点，用[1，2，3，…，n]表示。[Dij]表示由i地至j地的距离。一位销售员从地点1出发，然后到剩下的每个地点一次，最后回到地点1。那么其选择何种行走径路，能使总线路最短？货郎担问题（Traveling SalespersonProblem）是一种组合最优化的问题，其特点是方便描述，但难以解决[4]。

假设销售员是从地点1开始出发的。设销售员走到地点i，记为[Ni2，3，…，i-1，i+1，…，n]，表示由地点1到地点i之间中间地点的集合。

[S]表示到达地点i之前中途所经过的地点的集合，则[S?Ni]。

设[i，S]作为表示过程的状态变量。决策为由一个地点到另外一个地点，并定义最优值函数[fki，S]为从地点1开始出发，经由[k]个中间地点的[S]集到地点i的最短径路距离。故递推公式为：

[fii，S=minfk-1j，S?j+dji] （1）

其中，[j∈s]，[k=1，2，3，…，n-1]，[i=2，3，…，n]，[S?Ni]。

边界条件是[f0i，?=d1i]。

[Pk（i，S）]是最优决策函数，表示从地点1出发，遍历k个中间地点的[S]集至地点[i]的最短径路中临近[i]地前面的地点[5]。

2.2 最短巡回径路问题的平面坐标模型

假设有[n]个配送点，由集合[R=ri|ri=i，i=1，2，3，…，n]表示[6]。一辆货车从城市到达站送往每个配送点处，待配送完毕后再返回。用平面直角坐标系来表示点位，将n个配送点所在坐标置于直角坐标系中，定义决策向量[x]和y分别描述这n个配送点的坐标：

[x=xi|xi∈R；i=1，2，3，…，ny=yi|yi∈R；i=1，2，3，…，n] （2）

其中，对于所有的，j有[xi≠xj且yi≠yj]。此外，为构造数学模型方便，设以下变量：

[Qij=1， 车辆线路要经过i，j0， 车辆线路不经过i，j] （3）

则可以得到车辆配送优化的数学模型。

①车辆总的走行距离[7]：

[minW=i=0nj=0nCijQij ] （4）

②约束条件[8]：

[i=0nQij=1i=1，2，3，…，n （5）]

[j=0nQij=1j=1，2，3，…，n （6）]

[ Cij=xi-xj2+yi-yj212i≠j] （7）

[Qij∈（0，1） （8）]

式中：[W]表示遍历n个配送点最短巡回径路的距离；[Cij]表示从配送点i到配送点j的距离。

3 算法模型介绍

3.1 遗传算法

遗传算法（Genetic Algorithms）是从一个初始群体出发，来模拟生物进化过程，采用复制、交叉和变异等手段，在原有基因的基础上，产生具有更好性能指标的下一代解的集合，不断重复迭代，直到找到满意解或者最优解为止[9]。求解方法如下[10]。

①先确定遗传操作的代数k与种群规模n，然后设置初试代数k=1，使用随机数法产生n个初始可行解[Xi（1≤i≤n，k=1）]组成初始解群体。

②对当代群体中的所有个体[xik]，分别计算适应度[fXik]。

③while（！终止条件）；对于任意个体[Xik]，计算其生存概率[Pik：]

[Pik=fXik/fXik] （9）

根据[Pik]的大小，在群体中优良的个体进行遗传操作，包括运用复制、交叉和变异等手段得到新一代的解集合，然后使[k=k+1]，转到第②步。

④若满足条件，结束操作即可。

3.2 蚁群算法

蚁群算法（ant colony optimization）是模拟蚂蚁觅食的过程来对目标进行搜索，根据留在径路上的信息素浓度的高低，按概率选择接下来将到的地点[11]。径路上信息素的浓度越高，蚂蚁选择这条径路的概率就越大。求解方法如下[12]。

①一共m只蚂蚁，随机放在n个地点中，将第k只蚂蚁的禁忌表tabuk的第一个元素设置为蚂蚁k所在的地点，接下来选择地点表allowedk设置为除当前其所在地点之外的任意地点，设置各个径路上的信息素矩阵[m，n]。②每只蚂蚁依照各条径路上的信息素量高低，两地之间的距离和其他相关参数选择下一个地点。t时刻，蚂蚁k在地点i上选择地点j的概率[Pkij（t）]为：

[Pkijt=ταijtηβijts?allowedkταistηβist ， j∈allowedk 0 ，j∈allowedk] （10）

其中，[α]表征表示信息素重要程度的参数；[allowedk]表示蚂蟻k接下来要经过没有走过的地点；[β]表征启发式因子重要程度的参数，即两个地点距离的相对重要程度。

如果[allowedk]为0，那么表示完成一次旅行[13]。

③蚂蚁选择一次遍历的径路。

m只蚂蚁完成一次游历后，则各条径路上的信息素浓度依照下式更新：

[τijt+n=ρ?τijt+?τij] （11）

[?τkij=QLi，第k只蚂蚁在这次循环中经过ij边0，第k只蚂蚁在这次循环中没过ij边 （12）]

[ ?τij=k=1m?τkij （13）]

其中，[ρ]为信息素的蒸发系数，[Li]为本次循环经过路线的长度，Q为信息素增强系数。

4 数值实例

设某城市到达站的货物，由一辆货车配送到15个配送点处，各位置点处位置平面坐标如表1所示。若寻求最短巡回径路，降低配送成本，完成运输服务，求最佳配送径路。

4.1 试验硬件、软件环境

试验使用联想M40（14-inch）型计算机，处理器为2.6GHz Intel（R）Core（TM）i5，内存为4GB DDR3，操作系统为Windows7旗舰版，MATLAB版本为R2017a[14]。

4.2 数据结果对比

在遗传算法中，采用个体编码方式为实数编码，初始化的遗传参数设置为：初试种群大小为30，染色体基因个数为16，群体进化次数为400代（即迭代次数），交叉率为0.8，变异率为0.2，使用基于适应度比例的选择策略，即适应度越好的个体被选中的概率越大，且保存适应度最高的个体[15]；在蚁群算法中，设置初试的参数为：蚂蚁总数是30只，信息素重要程度设置为1，最大迭代次数为400代，信息素蒸发系数为1，信息素增强系数为100[16]。

两种算法结果对比如表2所示[17]。

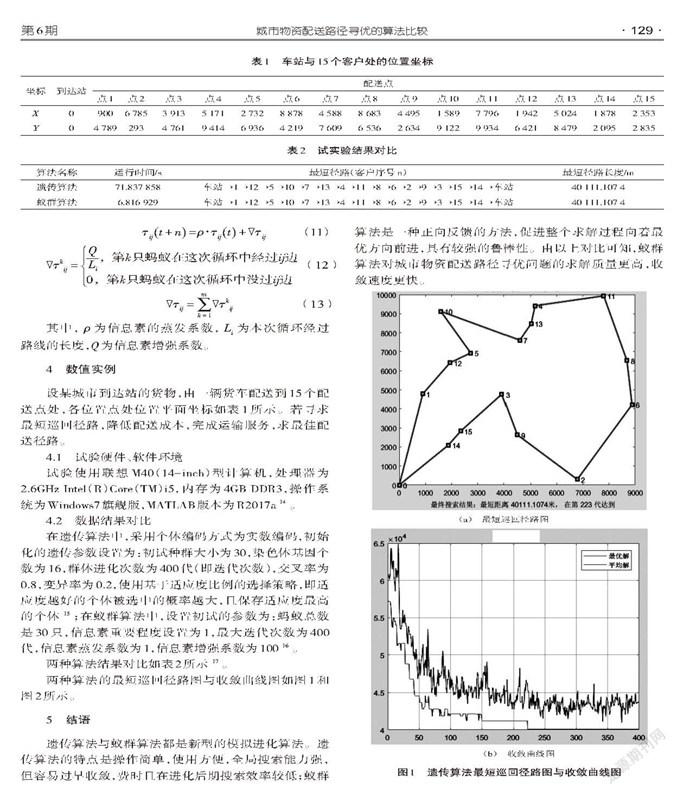
两种算法的最短巡回径路图与收敛曲线图如图1和图2所示。

5 结语

遗传算法与蚁群算法都是新型的模拟进化算法。遗传算法的特点是操作简单，使用方便，全局搜索能力强，但容易过早收敛，费时且在进化后期搜索效率较低；蚁群算法是一种正向反馈的方法，促进整个求解过程向着最优方向前进，具有较强的鲁棒性。由以上对比可知，蚁群算法对城市物资配送路径寻优问题的求解质量更高，收敛速度更快。

参考文献：

[1]杨浩.铁路运输组织学[M].北京：中国铁道出版社，2001.

[2]汝宜红.物流学导论[M].北京：清华大学出版社，2010.

[3]高自友，孙会君.现代物流与交通运输系统[M].北京：人民交通出版社，2003.

[4]徐帆.铁路快捷货物门到门运输组织研究[M].成都：西南交通大学，2015.

[5]徐天亮.运输与配送[M].北京：物质出版社，2012.

[6]燕忠.基于蚁群优化算法的若干问题的研究[D].南京：东南大学，2005.

[7]侯文静，马永杰.求解TSP的改进蚁群算法[J].计算机应用研究，2010（6）：2087-2089.

[8]王银年.遗传算法的研究与应用[D].无锡：江南大学，2009.

[9]吴庆洪，张颖，马宗民.蚁群算法综述[J].微计算机信息，2011（3）：1-2.

[10]刘利强，戴运桃，王丽华.蚁群算法参数优化[J].计算机工程，2008（11）：208-210.

[11]王超学，崔杜武，王竹荣，等.一种求解TSP的高效遗传算法[J].西安理工大学学报，2006（1）：37-41.

[12]王连山.关于遗传、蚁群、禁忌搜索算法的比较[J].电脑编程技巧与维护，2009（24）：18-21.

[13]楚艳娟.基于定位路径问题的配送网络规划研究[D].济南：山东大学，2008.

[14]梁栋，洪雁.我国铁路快捷货运产品设计及组织优化的探讨[J].铁道经济研究，2013（2）：15-19.

[15]王涵.物流企业配送网络区域划分研究[D].成都：西南交通大学，2012.

[16]陈俊勇.中国现代大地基准——中国大地坐标系统2000（CGCS2000）及其框架[J].测绘学报，2008（3）：269-271.

[17]边少锋，柴洪洲，金际航.大地坐标系与大地基准[M].北京：国防工业出版社，2005.