一种用于多类别划分的中心点选择算法

刘儒衡

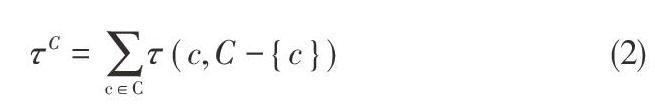
摘要：传统的 K-means 算法对初始聚类中心敏感，聚类结果随不同的初始输入而波动。当类别数目较多时，较好的初始聚类中心点集合的选择更为困难。针对K-means 算法存在的这一问题，该文提出一种用于多类别划分的中心点选择算法（MC-KM）。MC-KM通过放大中心点间长距离和短距离的影响的差距，增大短距离的比重，进而选择一个距离其他中心点都较远的样本作为中心点，然后使用传统K-means进行聚类。理论分析与实验结果表明， MC-KM在类数目较多的数据集中能取得更好的聚类结果，并且具有较好的稳定性。

关键词：聚类；MC-KM；K-means算法；初始中心点；相似度

中图分类号：TP181 文献标识码：A 文章编号：1009-3044（2018）12-0188-03

Abstract： The traditional K-means algorithm is sensitive to the initial clustering center， and the clustering results fluctuate with different initial inputs. When the number of categories is large， it is more difficult to choose a good initial cluster center set. Aiming at the problem of K-means algorithm， a central point selection algorithm （MC-KM） for multi class partition is proposed in this paper. By enlarging the gap between the long distance and the short distance between the center points， MC-KM increases the proportion of the short distance， and then selects a sample which is far away from the other center points as the center point， and then uses the traditional K-means to cluster. Theoretical analysis and experimental results show that MC-KM can achieve better clustering results in a large number of data sets， and has better stability.

Key words：cluster； MC-KM；K-means algorithm； initialized clustering centers； similarity

1 背景

聚类[1]是一种无监督学习方法，它将数据分成若干个类，使得同一个类中样本相似度较高，不同类中的样本相似度较低。目前，聚类方法在很多领域都有应用，包括图像模式挖掘、商务推荐、生物基因研究等[2]。常用的聚类算法可以分为基于划分的聚类、基于层次的聚类、基于密度的聚类、基于网格的聚类和基于模型的聚类等。

K-means聚类是一种基于划分的聚类方法。该算法采用自下而上的聚类结构，具有简单、速度快等优点，但传统K-means算法初始聚类中心的选择对聚类结果有较大的影响，一旦初始中心点选择的不好，可能无法得到有效的聚类结果。针对K-means算法的初始中心点选择困难以及聚类过程中存在的问题，该文从三个方面进行改进，一是定义新的相似度指标进行类中心点选择；二是多次选择中心点集合，选择相似度最低的中心点集合作为初始中心点集合；三是在聚类过程中，根据相似度剔除错误中心点，并重新选择更优的中心点。

2 相关工作

传统K-means 算法首先从数据集D中随机选择k个样本，每个样本代表一个类的初始中心点，根据距离将D中剩余样本分配到最近的类中，然后以一类中所有样本点均值作为各类新的中心点，重新分配D中对象，迭代该过程直到各个类的中心不再变化，得到k个互不相交的稳定的类。

K-means算法是一个局部搜索过程，其聚类结果依赖于初始聚类中心以及初始划分[2]， 并且 K-means算法的最终结果只是相对于初始划分更好，未必是全局最优的划分[3]。为了找到更好的中心点，诸多学者做了许多研究。Katsavounidis等人[4]提出基于最大最小法的初始中心点选择方法，该方法随机选取第一个中心点，其他中心点通过定义的最大最小指标进行选取。Erisoglu[5]等人通过定义的主轴进行中心点选择，初始中心由两个主轴确定，第一个初始中心为到主轴均值距离最大的样本。Wang[6]利用相异度矩阵构造哈夫曼树，从而选择 K-means算法的初始中心点。Bertalmio等[7]人提出确定性的聚类中心算法，根据样本的局部密度进行中心点的选择，取得了较好的效果。谢等人[8]通过样本方差进行中心点的选择。选择方差小且相距一定距离的样本作为初始中心点。钱等人[9]利用谱方法估计特征中心得到 K-means算法的初始聚类中心。尹等人[8]采取数据分段方法，将数据点根据距离分成k段，在每段内选取一个中心作为初始中心点，进行迭代运算。为了自动确定中心点的个数， Haslbeck等人[12]基于不稳定性方法进行估计类数目。?alik等人[9]考虑了数据的紧凑度和重叠度完成类别划分。Capó等人[10]提出一种用于海量数据下的均值近似计算方法。等人将k均值算法应用于图像和视频中文本信息挖掘。Khanmohammadi等人[11]提出了一个结合调和均值和重叠的混合方法k-均值的算法来解决医疗数据类别重叠的问题。Yeh等人[12]再KHM算法基础上提出快速集中化策略来提高收敛速度和最小的运动策略，有效地搜索更好的解决方案，而不陷入局部最优。Amorim等人[13]采用分布式加權质心的方法进行分布式k均值聚类直观的反应不同程度的不同集群的关联。Gan等人[14]采用k-mean进行离群点检测。Oliveira等人[15]采用加权特征空间的k-均值算法进行Terahertz图像的分割聚类。

通过点的密度、点的局部方差[16]、谱方法[17]进行中心点的选择都是确定性的方法，算法需要计算额外的信息，将算法时间复杂度变为O（n2）。在不改变时间复杂度情况下，单纯使用距离[18]的算法稳定性较差。该文提出DKM算法采用独特的相似度指标选择进行初始中心点的选择，在聚类的过程通过重选替换操作删除错误选择的中心点，来提高算法的容错率。DKM初始中心点选择与传统K-means相比较，不但在准确率等指标有所提高，而且大幅提高了算法的稳定性。在类别数目较多时，算法的聚类效果显著提高且相对稳定。

3 相似度指标

3.1 相似度指标

样本x到中心点集合C的相似度：

其中，[dx，c=x-cTx-c]为样本x到中心点c的距离。[λ]为放大倍数。相似度指标是在每个距离倒数基础上的进行[λ]倍放大。放大的目的是加大长短距离影响的差距，使长距离在求和中的作用变小，短距离在求和中的作用变大；当样本点距离某一中心点很近时，该距离在相似度指标中的作用占据主导地位。

3.2 MC-KM算法思想

该节介绍提出的改进的中心点选择算法MC-KM。MC-KM主要工作工作包括两个部分，第一部分根据公式（1）中相似度进行初始中心点选择；第二部分k次选择中心点集合，选择最优的中心点集合作为初始中心点集合。

为了更好地描述，称中心点集合中第一个被选择的中心点为衍生点。由一个衍生点出发可以得到一个中心点集合。算法首先确定一个样本x作为衍生点，并将x加入C，然后根据公式（1）计算每个样本与C的相似度，选择相似度最小的样本点加入集合C，直至C容量为k。

由于第一个点的随机选择，因此不能保证C为最优的中心点集合。为衡量集合的优劣，该文提出集合C内相似度指标。定义集合C的内部相似度为：

其中，C为容量k的中心点集合。該指标描述中心点c∈C与集合C-{c}的相似度之和。

若要得到最优的中心点集合，需要每个样本点作为衍生点，衍生出中心点集合，选择内部相似度最小的中心点集合，但这种方法时间复杂度为O（k2n2）。该文算法进行k次中心点集合选择，第1次衍生点随机选择，第i次衍生点为第i-1次衍生点距离最远的样本点，以此保证前后两次选择所采用衍生点属于不同类。由此衍生k次得到k个中心点集合，选择集合内部相似度最小的作为初始中心点集合。初始中心点的选取步骤描述如表1所示：

3.3 合成数据集上实验结果与分析

合成数据能够比较直观的表达展示算法的结果，本节采用三个类别相对较多的合成数据集来验证上诉选择和调整策略的有效性，并进行相应的分析。实验中采用的三个数据集分别为R15[19]、D31[19]、S-set1[20]，如图1所示，R15有15个类，每个类别大小、形状相似，且位置分布相对均匀；D31数据集有31个类，类别大小相差不大，位置分布相对杂乱；S-set1数据集有15个类，类别形状差别相对较大。

图1展示的是在数据集R15、D31、S-set1上选取的初始中心点。在R15数据集上，该文算法给每个类都选择到了一个正确的初始中心点，对于类别明确的数据，算法很好的选择出了初始中心点；在D31数据集和S-set1数据集上，虽然类比数目较多，分布杂乱，并且有些类距离很近，但是通过该文提出的指标仍然给出很好的初始中心点。仅有个别点受边界点和噪声点影响，中心点选择偏离相对较远。

图2展示的是在数据集R15、D31、S-set1上最终的聚类结果。在R15数据集上，由于正确选择初始中心点，因此能够正确聚类；在D31数据集和S-set1数据集上，虽然个别点选择错误，但通过选择调整策略，仍然得到正确的聚类结果。

3.4 真实数据集上实验结果与分析

该节在准确率、F值和标准化互信息NMI三个指标上对算法（MC-KM）与传统K-means算法（ORI-KM） 进行比较，来证明MC-KM的有效性。实验使用的数据集均来自于UCI数据库。

由图表2 的实验结果可以看出，MC-KM算法效果明显优于传统K-means算法。其中，iris和wine数据集都有两个类，MC-KM在三个指标上略有提升；而在Computer Hardware数据集上有5个类，Dermatology数据集有6个类，optdigits数据集上有10个类，MC_KM算法在这三个数据集上算法效果大幅提升，说明MC-KM算法的有效性。

4 结束语

传统K-means算法对于类别较多的数据初始中心点选择困难，且算法稳定性差，现有很多关于K-means的改进算法都需要获取额外的数据信息，算法时间复杂度为O（n2）。该文针对这一问题，提出了基于新的相似度指标的中心点选择策略，提高了算法的稳定性和准确率。在经典的人工数据集和UCI数据集上的实验结果表明，算法在多类别数据上更容易得到较好聚类中心点和最终结果。

参考文献：

[1] Han J， Kamber M. Data Mining： Concepts and Techniques， Morgan Kaufmann[J]. Machine Press， 2006， 5（4）： 394-395.

[2] Chan B T F， Shen J. Non-texture inpainting by curvature driven diffusions[C] （CDD）. J. Visual Comm. Image Rep， 2010.

[3] Pe?a J M，LozanoJ A，Larra?aga P. An empirical comparison of four initialization methods for the K-Means algorithm[J]. Pattern Recognition Letters， 1999， 20（10）： 1027-1040.

[4] Faber V. Clustering and the continuous K-means algorithm[J]. Los Alamos Science， 1994（22）： 138-144.

[5] Erisoglu M， Calis N， Sakallioglu S. A new algorithm for initial cluster centers in k-means algorithm[J]. Pattern Recognition Letters， 2011， 32（14）： 1701-1705.

[6] Wang S. An improved k-means clustering algorithm based on dissimilarity[C]// International Conference on Mechatronic Sciences， Electric Engineering and Computer， 2013： 2629-2633.

[7] Bertalmio M， Vese L， Sapiro G， et al. Simultaneous structure and texture image inpainting.[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society， 2003， 12（8）： 882-900.

[8] 谢娟英， 王艳娥. 最小方差优化初始聚类中心的K-means算法[J]. 计算机工程， 2014， 40（8）： 205-211.

[9] 钱线， 黄萱菁， 吴立德. 初始化K-means的谱方法[J]. Acta Automatica Sinica， 2007， 33（4）： 342-346.

[10] 尹成祥， 張宏军， 张睿， 等. 一种改进的K-Means算法[J]. 计算机技术与发展， 2014（10）： 30-33.

[11] Yeh W C， Lai C M， Chang K H. A novel hybrid clustering approach based on K-harmonic means using robust design[J]. Neurocomputing， 2016， 173（P3）： 1720-1732.

[12] Haslbeck J M B， Wulff D U. Estimating the Number of Clusters via Normalized Cluster Instability[EB/OL].http：//sciencewise.info/articles/1608.07494/.

[13] ?alik K R， ?alik B. Validity index for clusters of different sizes and densities[J]. Pattern Recognition Letters， 2011， 32（2）： 221-234.

[14] Aradhya V N M， Pavithra M S. A comprehensive of transforms， Gabor filter and k -means clustering for text detection in images and video[J]. Applied Computing & Informatics， 2016， 12（2）： 109-116.

[15] Khanmohammadi S， Adibei N， Shanehbandy S. An Improved Overlapping k-Means Clustering Method for Medical Applications[J]. Expert Systems with Applications， 2017（67）： 12-18.

[16] Amorim R C D， Makarenkov V. Applying subclustering and L p， distance in Weighted K-Means with distributed centroids[J]. Neurocomputing， 2016， 173（3）： 700-707.

[17] Gan G， Ng K P. k-means clustering with outlier removal[M]. Elsevier Science Inc， 2017.

[18] Oliveira G V， Coutinho F P， Campello R J G B， et al. Improving k -means through distributed scalable metaheuristics[J]. Neurocomputing， 2017（246）： 45-57.

[19] Veenman C J， Reinders M J T， Backer E. A Maximum Variance Cluster Algorithm[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence， 2002， 24（9）： 1273-1280.

[20] Fr?nti P， Virmajoki O. Iterative shrinking method for clustering problems[J]. Pattern Recognition， 2006， 39（5）： 761-775.

[21] Capó M， Pérez A， Lozano J A. An efficient approximation to the K -means clustering for massive data[J]. Knowledge-Based Systems， 2017（117）： 56-69.