弱电网下并网逆变器自适应H∞控制方法

马　兴, 徐瑞林, 陈民铀, 何国军, 付　昂, 董光德

(1. 国网重庆市电力公司电力科学研究院, 重庆市 401120; 2. 重庆大学电气工程学院, 重庆市 400044)

0　引言

在实际应用中,分布式光伏系统往往需要通过并网逆变器接入配电网中。考虑到配电网中较长的线路以及变压器的使用,电网表现为弱电网特性,即电网阻抗较大不能忽略[1]。在弱电网中,由于电网侧阻抗值未知,这一未建模干扰将会影响并网逆变器的稳定性和谐波畸变率,因此具有重要的研究意义[2]。

对于弱电网中并网逆变器的运行已经引起了广泛的重视,也取得了一些研究成果。文献[3-7]研究了电网阻抗对并网逆变器系统稳定性的影响机理,指出随着电网电抗的增大,稳定裕度减小,稳定性能降低。文献[8]进一步研究了电网阻抗对多个并网逆变器并联系统稳定性的影响。文献[9]指出为了克服电网电压的畸变对并网逆变器输出电流谐波含量的影响,往往需要引入电压前馈控制。文献[10]研究了弱电网下电网电压前馈控制的性能,指出弱电网下前馈控制本质上引入了电流正反馈通路,从而导致并网逆变器系统稳定裕度降低。为了提高并网逆变器系统在弱电网下的稳定性,学者们对弱电网下电压前馈改进控制方法进行了研究。文献[11]指出引起并网逆变器前馈控制不稳定的主要原因是延时在谐波频率处产生的相位滞后,提出了在前馈通道上增加带通滤波器的改进方法,在一定程度上增强了系统的稳定裕度。文献[12]提出了谐振前馈控制策略,抑制电压前馈中谐波频率分量的影响,并且不会对工频分量造成相位偏差。由于抑制前馈电压中谐波分量的方法并不能够完全消除弱电网特性对并网逆变器系统稳定性的影响。因此,文献[13-14]提出了对电网阻抗进行测量的方法,通过测量电网阻抗来修正前馈补偿电压以提高系统的稳定性,该方法理论上能够完全消除电压前馈控制的不稳定因素,然而电网阻抗的测量尚缺少有效的理论支撑,在实际电网中很难得到准确的测量值。这些方法均取得了一定的效果,但是针对弱电网下并网逆变器尚缺少简单有效的方法。

为了增强并网逆变器对电网阻抗变化的自适应能力以及简化控制策略的复杂程度,本文在传统非线性控制[15-18]的基础上,提出间接控制方法实现对电网阻抗变化的适应能力。在此基础上,采用H∞控制实现包含间接控制的并网逆变器系统的稳定。最后实验结果验证了本文所提控制方法的有效性。

1　弱电网下并网逆变器鲁棒H∞模型

弱电网中基于传统鲁棒H∞控制的并网逆变器系统如图1所示。其中,Udc为并网逆变器直流母线电压;L和R分别为并网逆变器输出滤波器的电感和等效电阻;Ls和Rs分别为电网阻抗中的电感和电阻;us为电网电压;upcc为公共连接点(point of common coupling,PCC)电压;is为逆变器并网电流。

图1　弱电网中并网逆变器系统Fig.1　Grid-connected inverter system in weak grid

由图1可知,并网逆变器系统的数学模型为:

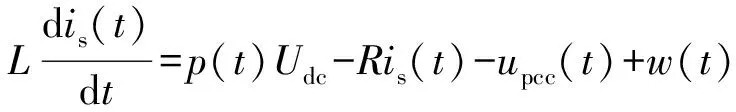
(1)

式中:p(t)为占空比函数;w(t)为死区效应造成的干扰。

进一步得到该系统的H∞系统模型为[18]:

(2)

考虑到弱电网特性,有

(3)

将式(3)代入式(2)中,即将弱电网对并网逆变器系统的影响代入,并将并网逆变器的误差系统模型改写为鲁棒H∞控制标准形式,则有[18-19]:

(4)

根据式(4)并且考虑到在弱电网条件下,电网侧阻抗的电感及电阻(Ls和Rs)的值是未知量,因此式(4)是一个系统参数、控制输入参数以及干扰输入参数均存在参数摄动的系统。由此可见,弱电网特性带来的影响是使得并网逆变器系统变为一个多个参数摄动的系统,并且参数摄动的形式(当仅有网侧电阻Rs时,则只有系统矩阵出现参数摄动;当仅有网侧电感Ls时,则系统参数、控制输入参数以及干扰输入参数均会出现参数摄动)和参数摄动的大小与电网阻抗有关。

本文将以一台单相并网逆变器为例,对电网阻抗的变化对并网逆变器系统的影响进行分析,其额定参数如附录A表A1所示。

2　电网阻抗变化对系统稳定性影响分析

由式(4)的相关参数表达式可以看出,电网侧电阻值Rs的变化仅会造成系统参数摄动,而电网侧电抗值Ls的变化会同时造成系统参数、控制输入参数和干扰输入参数同时出现参数摄动。因此,本文将分别研究电网侧电阻值和电网侧电感值变化对采用传统鲁棒H∞控制方法的并网逆变器系统稳定性和干扰抑制性能的影响。

考虑到数字系统延时和脉宽调制(PWM)的等效延时,则控制系统总延时时间为τ=τ1+τ2。其中,τ1为数字系统延时;τ2为PWM等效延时。由文献[19]可知,式(4)所示并网逆变器系统仅能取得时滞H∞控制器,控制器结构如下所示:

u(t)=Kx(t-τ)

(5)

式中:K为反馈系数。

由前面分析可知,当考虑电网侧阻抗变化时,并网逆变器系统的模型为:

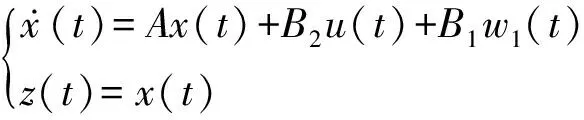
(6)

此时,将A表示为:

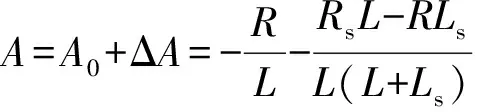
(7)

式中:下标0表示对应系数的已知部分;ΔA表示对应系数的摄动部分。

同理,将B2和B1分别表示为:

(8)

(9)

针对式(7)至式(9)中的摄动部分,可以将其表示成如下标准形式:

(10)

式中:H,E,Eb2,Eb1为常数;F(t)为具有Lebesque可测元素的未知实变参数,满足‖F(t)‖2≤1。

考虑延时的影响取Lypunov-Krasovskii泛函如下所示:

(11)

式中:P,X,Q为系数。

对于如式(6)所示并网逆变器系统模型,如果将系统参数、控制输入参数以及干扰输入参数中的参数摄动表达为式(10)所示标准形式,则在取能量函数为式(11)时,对于给定常数α1,α2和正实数γ>0,如果存在P>0,X>0,Q>0,存在实数Z11,Z22,Y1,Y2,Z12及正实数ε>0,使得式(13)和式(14)线性矩阵不等式组成立[20-21],则不确定时滞系统式(6)能够渐进稳定,且存在一类具有状态时滞信息的最优状态反馈H∞鲁棒控制律,其参数化表达式如式(15)所示[20]。

minγ

(12)

(13)

(14)

其中

Π11=AP+PA+2α1P+τZ11+QΠ12=B2K+(α2-α1)P+τZ12Π22=-2α2P+τZ22-Q

式中:γ为最优干扰抑制度。

u(t)=KP-1x(t-τ)

(15)

分别设置网侧电阻值Rs和网侧电抗值Ls为不同大小的值,以分别研究其大小变化造成的参数摄动对并网逆变器稳定性和干扰抑制性能的影响。并以无参数摄动时的干扰抑制度为基准值,定义干扰放大倍数β=(γ/γ0),其中γ0为无参数摄动时的干扰抑制度。

在电网侧电阻Rs从0 Ω增大至1 Ω的过程中,最优状态反馈控制器增益和干扰放大倍数几乎不发生变化。其中,控制器增益值从-12.021 2减小至-12.146 4,而干扰放大倍数从1增加至1.076。说明弱电网中仅有网侧电阻的情况下,弱电网特性造成的并网逆变器系统的参数摄动,即系统矩阵的参数摄动,总体来看,不会影响到并网逆变器系统的鲁棒稳定性。在干扰抑制能力方面,相对于无参数摄动时的理想情况下,网侧电阻对系统干扰抑制性能影响较小。

而随着网侧电感值Ls从0 mL增大至2.5 mL的过程中,最优状态反馈控制器增益从-12.021 2增加至-0.248 0,在Ls较大时,最优状态反馈控制器增益接近于0,因此并网逆变器系统接近于开环运行,最优状态反馈控制器几乎不起作用,并网逆变器的闭环鲁棒稳定性大为减弱。同时,随着Ls的增加,干扰放大倍数急剧增加从1增加至89.94,严重地放大了干扰的影响,并网逆变器系统会出现较大的稳态误差。当网侧电阻和网侧电感同时变化时,由于如式(6)所示系统为一个线性系统,因此参数摄动造成的影响可以采用叠加定理进行计算。

3　弱电网下并网逆变器控制策略设计

3.1　间接控制

通过前面的分析可知,由于弱电网特性的影响使得PCC电压中包含了状态变量的动态,从而造成了采用传统鲁棒H∞控制方法的并网逆变器模型变为了一个系统矩阵、控制输入矩阵和干扰输入矩阵均出现参数摄动的系统,影响了闭环系统的稳定性和干扰抑制性能。因此如果能够不直接采样upcc(t)作为电压前馈,而通过合适的间接控制方法动态地调节PCC电压,使其不包含系统状态变量的微分项,并且能够使得系统实现对给定电流的跟踪,则系统中将不会出现系统矩阵、控制输入矩阵以及干扰输入矩阵的参数摄动。间接控制部分的示意图如附录A图A1所示。

本文所提间接控制的传递函数模型如图2所示。图中:Iref为电流给定值的幅值;Is1p和Is1q分别为is的基波有功电流和基波无功电流的幅值。间接控制中电流控制器采用的是积分控制。一阶惯性环节是代表控制系统的延时T=τ。为了证明间接控制的稳定性以及研究其稳态精度,将离散傅里叶变换(DFT)环节进行等效变换,变换后的表达如虚线框内所示。其中,间接控制采用的是积分控制,ki为积分环节的系数。

图2　间接控制传递函数Fig.2　Transfer function of indirect control

由于有功电流控制和无功电流控制传递函数结构相似,以下仅以有功电流控制为例进行分析。容易看出有功电流控制具有一个输入量Iref和一个干扰量us。在间接控制中,输入量作用下的传递函数与干扰量作用下的传递函数的特征多项式相同,均为:

TLss3+(TRs+Ls)s2+Rss+ki=0

(16)

对于式(16),由于T,Ls,Rs,ki均为正实数,因此劳斯表中第1列中第1行、第2行、第4行元素均为正号。因此,由劳斯判据只要保证劳斯表中第1列第3行也为正,则系统稳定。即有

(17)

可见,满足大范围稳定的ki的设计仅与Rs的最小取值有关,与Ls的取值无关,因此大大简化了ki取值的设计。在本文中,计算ki的范围时,由于网侧等效电阻均超过了0.01 Ω,因此取Rs=0.01 Ω,则ki<66.7。通过以上分析,如果取ki<66.7则间接控制系统稳定。

在系统稳定的基础上,以下将进一步分析间接控制系统的稳态误差。在阶跃型输入量作用下的稳态误差可以采用终值定理进行计算。可得在输入量作用下的稳态误差ess1为:

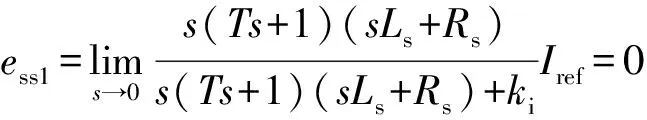
(18)

在干扰量作用下的稳态误差,由于us是一个正弦函数,不能直接采用终值定理进行计算。为了简化稳态误差的计算,将us表示为:

(19)

式中:Usp和Usq分别为电网电压以upcc(t)为相位基准的有功分量幅值和无功分量幅值。

然后分别求取Usp和Usq所引起的稳态误差ess2和ess3,如果ess2和ess3均为0,则us(t)引起的稳态误差为0。ess2和ess3分别为:

(20)

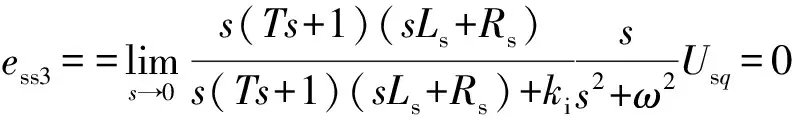
(21)

3.2　改进H∞控制

在采用间接控制方法后,要求间接控制能够动态地估计并调节PCC电压的值,从而使得系统在电网阻抗变化的情况下能够实现对给定电流的跟踪。然后通过状态反馈H∞鲁棒控制实现整个系统在间接控制动静态过程中的渐进稳定性并减小谐波含量。采用本文所提的改进H∞控制(即包含间接控制的H∞控制)方法的并网逆变器控制系统控制模型如下所示:

(22)

其中

参照第2节中方法,可以求得使得如式(22)所示系统渐近稳定的具有状态时滞信息的最优状态反馈H∞鲁棒控制律。具体推导过程如附录B所示。由于A0,B20和B10的值均为逆变器侧的参数与电网阻抗的值无关,是已知的常量,因此使得并网逆变器系统渐近稳定的状态反馈控制器增益范围不受电网阻抗变化的影响。对应的干扰抑制能力也与电网阻抗无关。

(23)

因此,可以将系统改写为:

(24)

其中

4　实验验证

为了验证前面的理论分析,根据附录A表A1中的参数在搭建了额定功率为5 kW的弱电网下的单相桥式并网逆变器实验平台,其电路拓扑如图1所示。其中控制器采用了TI公司的TMS320F28335,绝缘栅双极型晶体管(IGBT)模块为Infineon公司的FF100R12KS,直流侧为直流可调稳压电源。在实验中,通过在电网侧调节大功率可调电阻RX20ZG11-200A-5RJ和串联不同大小的电感来模拟电网阻抗的变化。

首先,为了验证电网侧阻抗对采用传统鲁棒H∞控制方法的影响以及本文所提改进H∞控制方法的有效性,分别在电网侧阻抗取不同值时,对采用传统鲁棒H∞控制方法(方案1)、本文所提改进H∞控制方法(方案2)与采用文献[14]中的自适应电流控制方法(方案3)的并网逆变器稳态结果进行对比,其结果如图3所示。

由图3可知,当电网侧电感为2 mH时,对方案1影响较为明显,并网电流明显的小于给定电流值,说明方案1方法不适用于电网侧电感较大的场合。方案2和方案3均能取得较好的控制效果。由于方案3中对电网侧电感的检测计算有误差,计算结果为1.8 mH,方案3相位偏差和电流畸变较方案2略差,其中方案2的相位偏差为1.6°,方案3的相位偏差为4.3°;方案2的电流总畸变率为1.43%,方案3的电流总畸变率为1.86%。

图3　网侧电感为2 mH时3种方案的实验结果Fig.3　Experimental results of three strategies when grid-connected inductance is 2 mH

电网侧电阻的变化时3种方案均能准确跟踪给定值且波形畸变很小。电网侧电阻取1 Ω时的实验波形如附录A图A2所示。因此,电网侧阻抗变化对三种方案的稳态精度影响较小,可以忽略。

在网侧电感取为2 mH时,对方案2和方案3的动态性能进行对比,实验结果如图4所示。

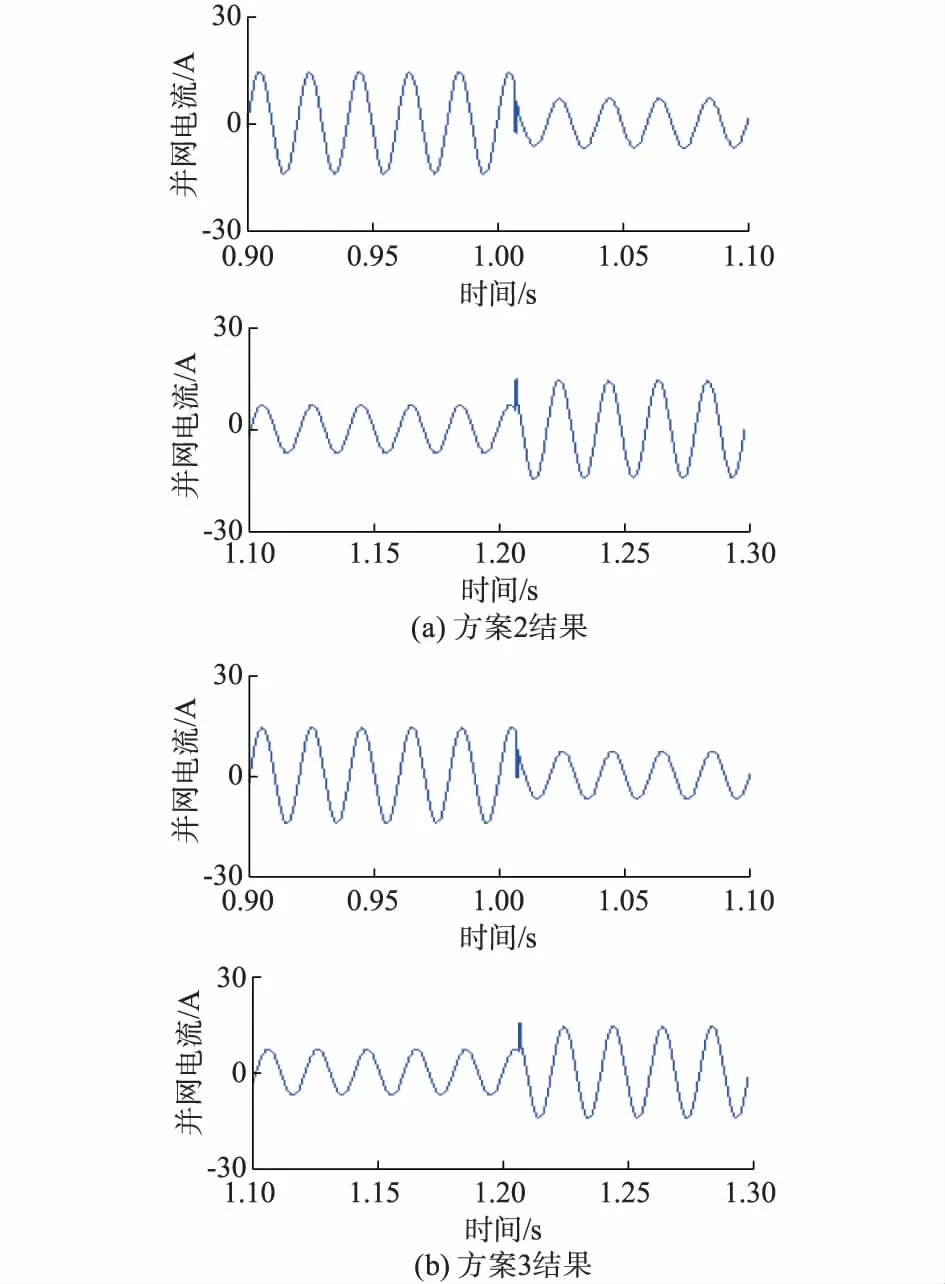
图4　负载突变时2种方案的实验结果Fig.4　Experiment results of two strategies when load changing

由负载突卸和负载突加实验结果可以看出,方案2较方案3动态性能会差一些,方案在系统受到干扰后约需要一个工频周期进入稳态,这是由于在间接控制中采用了DFT,DFT具有一周期的延迟,因此影响了系统的动态性能。如果采用更快速的基波检测方法,能够进一步提高方案2的快速性。但是方案2无需对电网阻抗进行测量,通过合理的参数设置可以实现对大范围电网阻抗的自适应。相对于方案3当电网阻抗出现变化时,需要重新测量更具有优势。

5　结语

本文研究了基于传统鲁棒H∞控制的并网逆变器在弱电网下运行的问题,分析了电网阻抗对采用传统鲁棒H∞控制的并网逆变器系统控制精度的影响机理,提出了改进H∞控制方法。通过引入间接控制方法使得系统对弱电网具有自适应特性,并给出了间接控制稳定性严格的证明以及控制参数的选取方法。然而,当配电网中电压畸变较为严重时,电网电压中的谐波分量会作为干扰量造成间接控制稳态精度降低。如何在同时考虑电网阻抗变化和电网电压畸变时,保证系统的渐近稳定性以及减小输出电流谐波含量,是下一步需要继续研究的问题。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。