基于自适应采样序列长度的全相位DFT同期并网参数测量

丁　明, 姚宇亮, 李　林,, 史盛亮, 毕　锐, 曹　军

(1. 安徽省新能源利用与节能实验室(合肥工业大学), 安徽省合肥市 230009; 2. 科大智能(合肥)科技有限公司, 安徽省合肥市 230080)

0　引言

传统的同期方案包括硬件测量和软件算法[1],硬件测量易受谐波噪声影响、抗干扰能力较弱,软件算法则易受频谱泄漏的影响。常见的软件算法以傅里叶变换为基础实现[2-3],但是在非同步采样时会因为频谱泄漏造成较大误差[4],通常采用加窗函数和频谱校正来改善测量精度[5-9]。对于光储微网的同期并网情况,文献[10]指出基于电力电子装置的逆变器型的分布式电源和微网没有调速系统和励磁调节系统,惯性小、动态响应快,远高于同步发电机组;逆变器型微源输出阻抗、单机容量和过载能力远小于传统同步电机,并网要求更高。传统的同期并网策略已经不足以满足光储微网的并网要求。

考虑到分布式电源和微网中大量电力电子器件的应用将产生大量谐波和噪声[11-13],光储微网内部光伏出力的随机变化和负荷的随机波动,导致自身频率变化和谐波的产生无法预测[14],可近似认为光储微网公共连接点(PCC)处的电压是在一定范围内随机波动的信号,并网环境恶劣且并网参数测量困难。若用固定长度的矩形窗来截断PCC处的电压信号,则无法做到周期截断,将会造成频谱泄漏及采样的误差[9]。为提高采样的精度,抑制非同步采样造成的频谱泄漏,本文提出了基于自适应采样序列长度的全相位算法。算法首先通过计算两段采样序列的相关性,自适应获取PCC两侧的采样序列长度,再利用全相位算法获得光储微网PCC两侧电压的频率、幅值和相位,并作为同期并网的判据。

1　自适应全相位DFT同期并网策略

1.1　自适应获取采样序列长度

周期信号如果被整周期采样,傅里叶变换不会产生频谱泄漏[7]。序列的周期性采样可由同一信号时域上连续采样获得的相同长度的两段离散序列的相关性评价。等间隔采样获得的离散的长度为N的序列可视为一个N维向量,通过采样获得连续的两段长度为N的离散序列的相关性可以通过向量的内积来衡量[15]。离散序列a和b的内积计算公式如下:

〈a,b〉=‖a‖‖b‖cosθ

(1)

式中:‖a‖和‖b‖分别为向量a和b的范数;θ为向量a和b的夹角。

由式(1)可知,向量a和b的内积的值在向量a和b的模不变的情况下由θ决定。分析易知在周期性采样时,两段序列完全相同,其对应的夹角θ=0°,此时向量的内积最大;非周期采样时两段序列值不同,θ≠0°,此时内积小于周期性采样时的内积,且cosθ∈[-1,1]。定义相关系数K来量化两段序列的相关性:

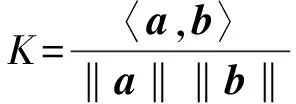
(2)

为方便量化计算,‖a‖和‖b‖取2-范数计算时K∈[-1, 1]。根据向量和序列的关系,K值越大,序列的相关性越大,K值越小,序列相关性越小,K=1时序列完全相关,K=-1时序列完全不相关。

以单频信号s=5sin(100πt+30°)为例,进行等距采样,每周期采32点,不同相关系数对应的傅里叶变换频谱见附录A图A1。可知频谱泄漏和相关系数的定性关系如下:当相关系数K=1时,为整周期采样,没有频谱泄漏;当K>0.9时,频谱泄漏很小,频谱的幅值误差很小;随着K的减小,频谱泄漏越来越严重,频谱幅值误差增大;当K=-1时,频谱泄漏最为严重。因此通过设置合理的相关系数值,计算采样序列的相关系数,自适应获取采样序列长度,可以提高序列的周期性采样,减小频谱泄漏。

光储微网同期并网电压参数测量过程中,光储微网内部光伏出力的随机变化和负荷的波动,以及大量电力电子器件及其复杂的控制策略决定了PCC处的电压信号不是一个严格的周期信号,不可能得到K=1的两段序列,即不可能做到整周期采样。为减小采样造成的误差,需选择合适的序列长度,并保证局部周期性。通过采样获得两段长度相等的序列,计算相关系数K,设定合适的相关系数阈值Kc,以确定合适长度的采样序列。结合同期并网的具体实际,序列的长度不宜过短和过长,因序列过短无法保证精度,而过长的序列则导致实时性差、计算量大。设定序列长度的最小值Nmin和最大值Nmax,若在(Nmin,Nmax)内无满足自适应的序列,则序列长度取最大值。获取自适应长度序列的流程如图1所示。

由于不可能做到周期采样,利用序列S1或S2进行离散傅里叶变换(DFT)计算获得其基波的频率、幅值和相位存在频率泄漏,同时仅用一段序列进行计算会造成采样序列的浪费。为进一步抑制频谱泄漏、充分利用采样序列、提高计算精度,引入全相位算法对两段采样序列进行处理。由于上述序列采样过程的序列长度不固定,而快速傅里叶变换(FFT)对序列长度的要求是2的整次幂,DFT对序列的长度没有特别的要求[16],因此本文选用全相位DFT作为处理算法。

1.2　全相位DFT

文献[17]从理论上证明了双窗全相位DFT比传统加窗DFT具有更优的频谱泄漏抑制性能,且全相位DFT具有相位不变性,主谱线的相位谱等于序列中心采样点相位理论值等性质,能够方便获得采样信号的高精度相位信息。

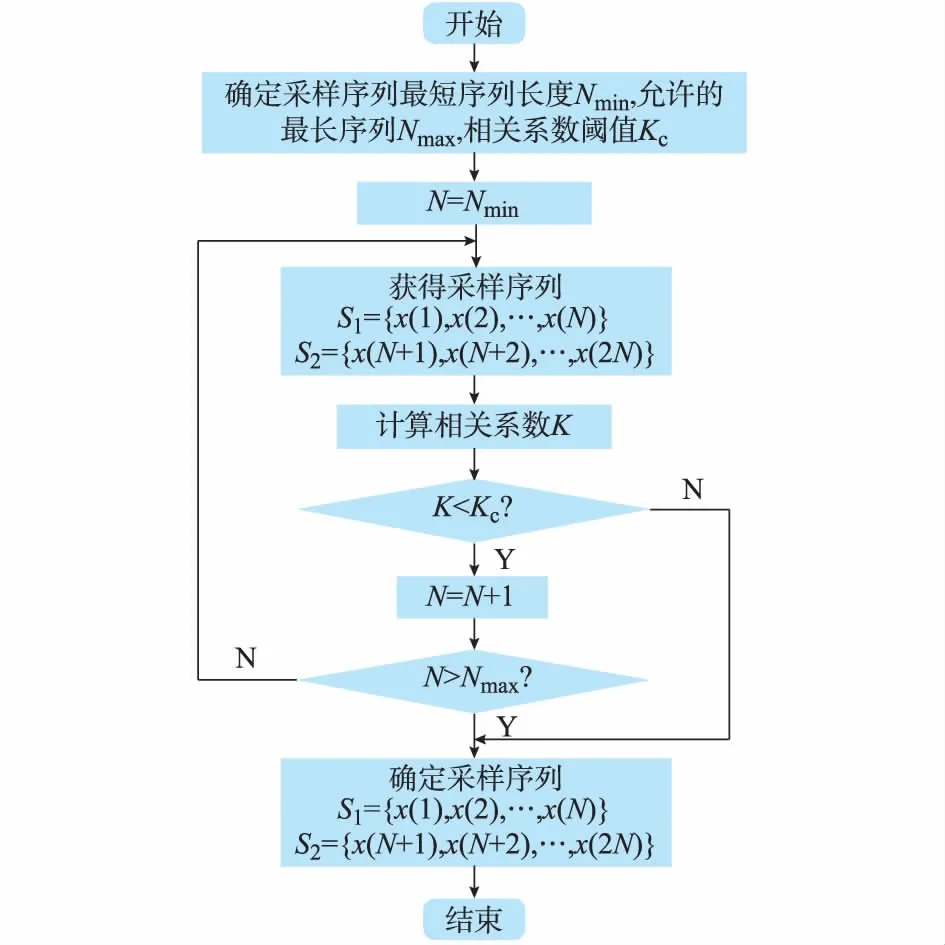
图1　自适应序列采样流程Fig.1　Flow chart of adaptive sequence sampling

全相位DFT包括预处理和DFT计算两个部分,计算过程见附录A图A2[17-19]。全相位DFT是对长度为2N-1的序列进行加卷积窗处理后间隔为N的数据两两相加,得到一个新的长度为N的序列,对新序列做DFT得到全相位频谱,通过对全相位DFT频谱进行相应处理即可得到信号频率、幅值和相位信息[19]。附录A图A2中的卷积窗ωc(n)可由相同长度的前窗f和后窗b翻转后卷积获得,即

ωc(n)=f(n)*b(n)

(3)

由文献[18]可知,对于单频信号有：

|Y(m)|=|X(m)|2=A|F(kΔω-ω*)|2

(4)

式中:|Y(m)|为全相位DFT第m条谱线的幅值;|X(m)|为传统加窗DFT第m条谱线的幅值;A为单频信号幅值;|F(ω)|为窗函数频谱幅值;Δω为频率分辨率;ω*为信号的频率；k为频谱中主谱线对应的位置。

由式(4)可知,单频信号全相位DFT频谱幅值是传统加窗DFT频谱幅值的平方,使得旁瓣谱线与主谱线的比值按照平方衰减,能够进一步抑制频谱泄漏[18]。

全相位DFT要求采样序列的长度是2N-1,计算相关性的两段序列的总长度是2N,因此对两段序列进行全相位DFT处理时要舍去一个采样点。为保证两段序列的连贯性,本文舍去序列S1的第1个采样点,与S2合并组成长度为2N-1的序列。选择旁瓣较小的汉宁窗做自卷积后对序列进行预处理获得长度为N的新序列,对新序列进行DFT运算获得序列的频谱,中心样点是x(N+1)。全相位DFT对序列做了全新的处理,传统的DFT频率、幅值、相位的计算方法不再适用。文献[17]介绍了包括时移相位差法、FFT+DFT连续谱细化法、双谱线法等方法。双谱线法仅需利用DFT计算几条谱线即可精细估计信号的频率幅值和相位,计算量较小、实时性好,因此本文采用双谱线法精细估计信号的频率、幅值和相位。

令ω*=k*Δω,其中Δω=2π/N,k*为信号频率在频谱上对应的位置,在N较大时,令δ=k-k*,则汉宁窗的频谱函数可化简成式(5)。

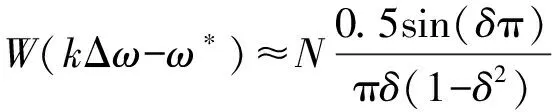
(5)

根据文献[17],双谱线法校正包括两种情况,分别见附录A图A3(a)和(b),频率估算公式由主谱线和幅值较大的旁谱线校正获得,两种情况下的估算公式存在差异。为归一化频率估算公式,对谱线进行统一编号。设所求信号的谱线是k*,k是主谱线和较大旁谱线中较k*向上的谱线,k-1是较k*向下的谱线,分别见附录A图A3(c)和(d)。根据式(5),第k条谱线和第k-1条谱线的幅值为:

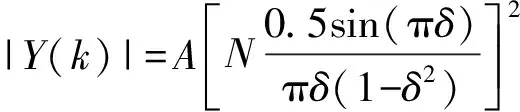
(6)

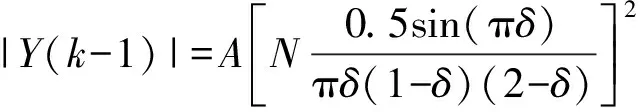
(7)

式(6)、式(7)相除得到:

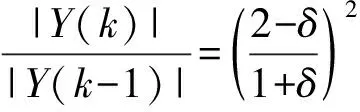
(8)

由于|Y(k)|和|Y(k-1)|是全相位DFT第k和k-1条谱线的幅值,因此通过式(9)可以求出δ,进而通过式(10)求出信号频率的估计值ω*。

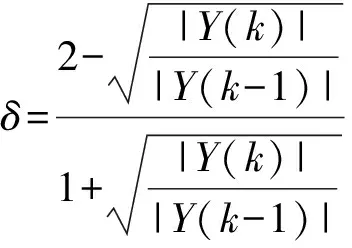
(9)

ω*=(k-δ)Δω

(10)

获得频率估计值后,对信号的幅值进行估计,对同期并网而言,需要基波电压的信息,可认为是提取单频信号的信息,单频信号的主谱线幅值如式(4)所示,因此基波信号幅值A的估计公式为:

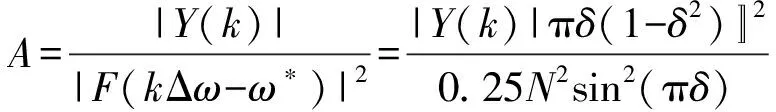
(11)

根据全相位DFT的性质,基波主谱线上的相位谱值等于输入序列的中心样点相位值[17],而同期并网策略要求实时的相位值,即最后一个采样点相位的实时值。因此在计算出中心样点的实时相位值θ0后,由下式计算相位的实时值:

θ=θ0+2πf*(N-1)Ts

(12)

式中:f*为经全相位DFT后估算出的信号频率,经自适应获得的两段序列,舍去第1段序列的第1个点构成长度为2N-1的序列,中心样点为x(N+1),最后的采样点距中心点的距离为N-1;Ts为采样周期。

1.3　自适应全相位DFT计算流程

综上,基于自适应序列的同期并网参数测量的算法流程如下。

1)根据图1流程获得PCC一侧电压的自适应长度的采样序列S1和S2,确定序列长度N。

2)生成长度为N的汉宁窗,自卷积获得长度为2N-1的卷积窗。

3)舍去S1的第1个采样点x(1)后合并序列S1和S2,对合并序列进行汉宁双窗全相位预处理,并确定基波在频谱所在位置周围的几条谱线的DFT频谱值。

4)找到其中的主谱线,并比较主谱线前后旁谱线的大小,确定主谱线和较大旁谱线在频谱中的位置,记为k和k-1,并计算|Y(k)|和|Y(k-1)|。

5)根据式(9)计算出δ,代入式(10)、式(11)求出基波电压的频率和幅值,再根据式(12)计算出最后采样点的相位作为实时相位信息。

6)对PCC另一侧进行上述重复操作，获得基波电压的频率、幅值和相位。

7)比较PCC两侧电压频率、幅值、相位是否满足并网要求,给出允许并网信号。

2　仿真分析

本文提出的算法是在自适应获取采样序列的基础上,进行全相位DFT处理并获得并网参数测量值。文献[17]在理论上证明了双窗全相位DFT比加窗DFT具有更高的精度,因此仿真实验设计了包括与固定序列全相位DFT在基波频率随机变化、同时含有谐波和噪声时的精度比较,以及非稳态信号下算法的精度,以验证算法是否适用于光储微网的同期并网参数测量。

当前国内还没有出台相关微网同期并网的技术标准,仅有一些文献提出一些并网条件[20]。IEEE 1547相关标准[21-22]指出的微网并网参数标准见附录A表A1,可知IEEE 1547对微网同期并网参数标准中的并网参数精度提出了较高的要求,尤其是对频率偏差的要求。因此,对并网参数的测量方法精度提出了较高要求。

为验证算法的精度是否满足上述标准要求,在MATLAB上进行了仿真。仿真考虑光储微网内部光伏随机性和负荷波动性,并网点的电压波形不是严格的周期信号,基波频率和谐波、间谐波的含量在一定范围内随机变化,因此在仿真过程中加入随机函数来模拟光储微网PCC处的电压波形。考虑到光储微网在允许并网前微网的基波频率和谐波含有率应满足国家电网发布的相关技术规定和IEEE 1547相关标准[21-22],在仿真信号中加入谐波和噪声,观察在谐波含量丰富的环境下，算法能否较为准确地测量出基波的频率、幅值和相位。

通过MATLAB进行大量仿真计算,在包含谐波和噪声的情况下,在采样序列为8个周期时,其相关系数均在0.85左右,此时的频谱泄漏较小,同时全相位DFT处理过程中进一步削弱了频谱泄漏,可以得到精度较高的计算结果。因此在相关系数无法满足设定的阈值时,采用序列最大值进行计算。在下列仿真分析中,采样频率设置为6 400 Hz,Nmax取1 024。为保证算法的精度,采样序列至少为一个周期,因此Nmin取128。

2.1　基波频率随机变化仿真

为验证本文提出的算法在基波变化情况下的精度,结合并网情况下基波频率允许值,设定信号模型的基波频率在(49.5,50.5)Hz之间变化,以0.1 Hz为间隔分成10个区间,在区间内基波频率随机变化,各次谐波幅值根据GB/T14549—1993[23]规定的最大值给定。信号模型如下：

S(t)=A0+A1cos(2π(f+arand(1))t+θ1)+

(13)

信号模型中令A1=1,A0=Ai=0.05。rand(1)表示随机产生(0,1)内的随机数,a取值为(-0.5,-0.4,…,0.4,0.5)。仿真采用蒙特卡洛模拟[24],即每个区间内按重复20次求平均的方式获得固定序列全相位DFT和自适应序列长度全相位DFT的基波频率、幅值、相位测量误差,结果如图2至图4所示。

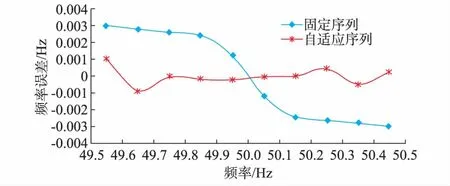
图2　基波频率测量误差Fig.2　Measurement errors of fundamental frequencies

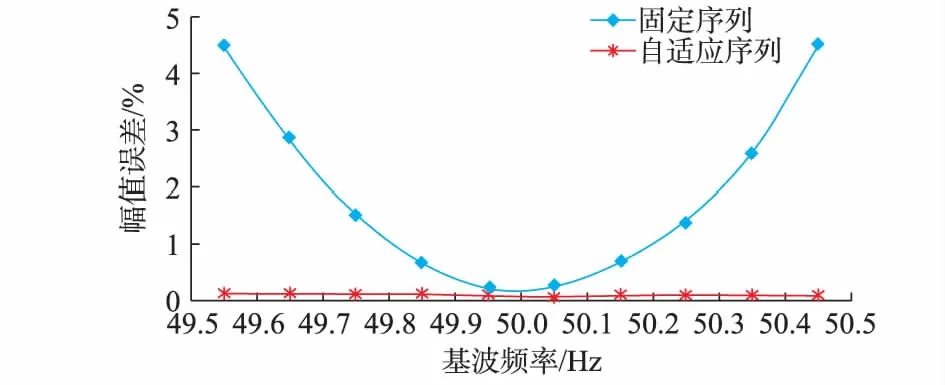
图3　基波幅值测量误差Fig.3　Measurement errors of fundamental amplitudes

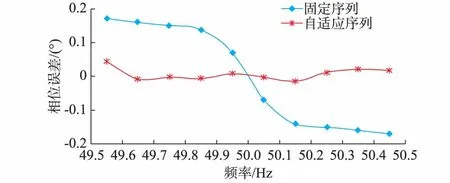
图4　基波相位测量误差Fig.4　Measurement errors of fundamental phases

由图2至图4可知,在谐波丰富的环境下,基波频率偏移对固定序列全相位DFT测量精度的影响较大,基波频率偏移越大,固定序列全相位DFT的基波频率、幅值、相位误差越大,尤其是相位误差,在基波频率偏移超过0.3 Hz时,相位误差超过了0.15°,这是因为频谱偏移导致无法实现同步采样,造成频谱泄漏。而自适应序列长度全相位DFT能够通过自适应获得采样序列,有效地抑制基波频率偏移造成的误差,在基波频率偏移达到0.5 Hz时,其相位误差不足0.05°,因此自适应序列长度全相位DFT在基波频率偏移较严重的情况下依然具有较高精度,说明算法在频率发生较严重偏移时的测量精度要高于固定序列获得的测量参数。

2.2　含有噪声和谐波仿真

在微网并网过程中,需考虑系统环境噪声和微网内部产生的谐波的影响。为分析噪声和谐波存在情况下对算法精度的影响,令仿真信号模型为:

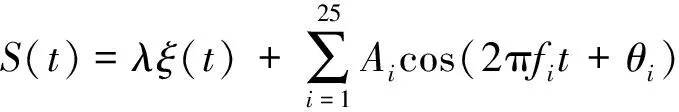
(14)

ξ(t)是均值为0、方差为1的高斯白噪声,结合文献[17],A1取1,λ分别取0,0.5,2对应的信噪比为+∞,15.05 dB和3.01 dB,也即对应无噪、低噪和高噪的情况。各次谐波幅值根据GB/T14549—1993[23]规定的最大值给定,每种情况下对固定序列全相位DFT和自适应序列全相位DFT进行100组蒙特卡洛模拟[24],结果如表1所示。

表1　噪声环境下固定序列与自适应序列全相位DFT误差Table 1　Errors of fixed sequence all-phase DFT and adaptive all-phase DFT in noisy environment

由表1可知,无噪环境下,固定序列长度全相位DFT和自适应序列全相位DFT都具有很高的精度;在低噪环境下,固定序列全相位DFT和自适应序列全相位DFT的误差均有升高,而固定序列全相位DFT误差升高更明显;在高噪环境下,固定序列全相位DFT和自适应序列全相位DFT的误差继续升高,且固定序列全相位DFT的幅值误差和相位误差分别为7.356 852%和3.236 854°,已经远远超过并网参数测量精度要求。而自适应序列全相位DFT的误差虽有升高,但基波的频率、幅值和相位的测量精度依然较高。

2.3　非稳态信号下仿真分析

在电网波动时,基波信号是幅值和频率会发生变化的非稳态信号,因此有必要验证在基波是非稳态信号时的算法精度。非稳态信号模型如下:

S(t)=A1′(2πf1′t+θ1)+λξ(t)+

(15)

式中:A1′=0.95+0.1t,f1′=49.5+0.1t,λ取0.5,各次谐波取值为GB/T14549—1993[23]规定的最大值,1～10 s时间段内的测量误差如图5所示。

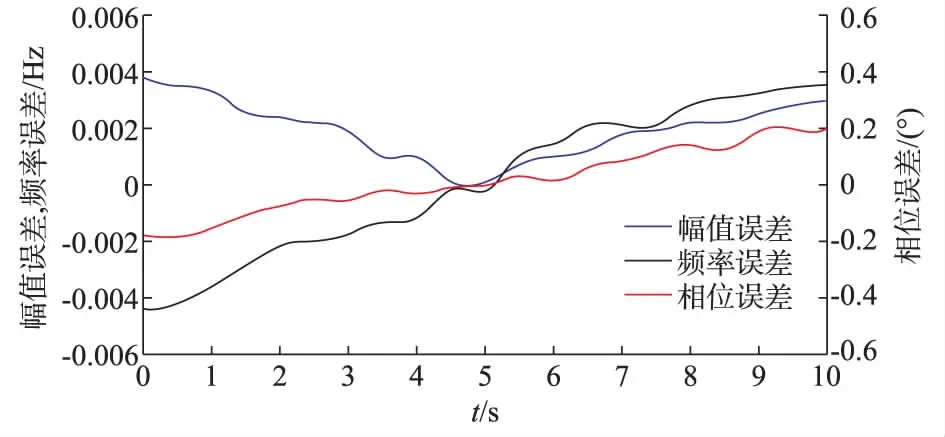
图5　非稳态信号测量误差Fig.5　Measurement errors of unsteady state signal

由图5可知,在非稳态信号情况下,由于基波信号的幅值和频率在时刻发生变化,且信号中加入了噪声和谐波,对测量精度造成一定影响,但从测量结果可知,算法的频率测量误差小于0.005 Hz,幅值误差小于0.4%,相位测量误差小于0.2°,依然具有较高的测量精度。同时从测量结果可知,在1～3 s和8～10 s内误差偏大,此时由于频谱偏移较严重,为保证算法的计算速率,Nmax取值限制了获得相关系数更高的采样序列,算法抑制频谱泄漏的能力减弱,导致测量误差偏大。

3　实际应用

由于同期并网参数的测量对测量时间和精度都具有较高要求,因此为验证算法的实时性和精度,设计了以STM32F407为CPU的实验测试平台,实验平台构成见附录A图A4。

利用继保测试仪模拟同期并网两侧的电压输入信号,信号的基波幅值给定为100 V,频率从49.5～50.5 Hz以0.1 Hz间隔变动,谐波幅值根据GB/T14549—1993[23]规定的最大值给定,实验平台采样频率为1 600 Hz,Nmin取32,Nmax取128,STM32F407实验平台上算法的最大运行时间为4 ms,测量结果如表2所示。

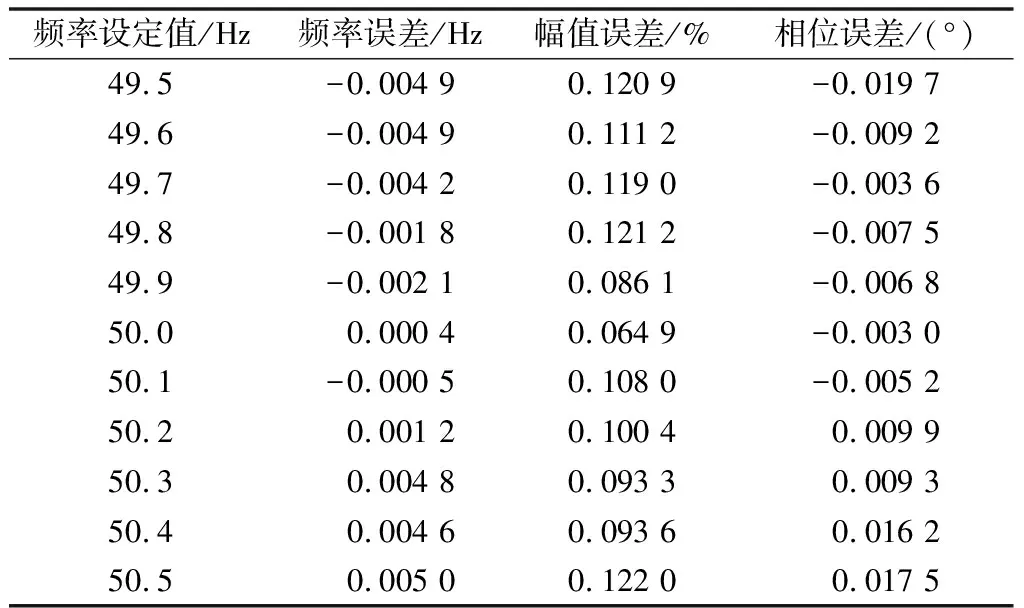
表2　STM32F407实验平台算法测量误差Table 2　Measurement errors of algorithm based on STM32F407 experiment platform

由表2可知,基于自适应序列全相位DFT算法在STM32F407实验平台频率测量误差小于0.005 Hz,幅值测量误差小于0.13%,相位测量误差小于0.02°,测量精度较高,具有一定的实际应用前景。可知,当基波出现频率偏移较严重时,误差会增大,这是由于为保证算法的实时性,Nmax取值导致在采样序列无法获得相关系数足够大的采样序列而造成的测量误差。

4　结语

本文提出的基于自适应序列长度的全相位DFT算法优化了序列的采样过程,同时利用全相位DFT抑制频谱泄漏的优良性能,在基波频率发生偏移、谐波和噪声含量丰富,以及非稳态信号环境下能够有效地抑制非同步采样造成的频谱泄漏,获得较高精度的基波信息,这也是本文提出算法的优势之一。同时,利用双谱线频谱校正思路推导的基于汉宁窗的双窗全相位DFT的基波频率、幅值和相位估算公式简洁,在硬件中容易实现。但是该方法在进行仿真验证和在实验平台进行实验时,仿真环境和实验条件有限,无法真正模拟光储微网的PCC处的电压真实情况,仿真实验结果具有一定的局限性。下一步的工作重点是进一步优化算法流程,提高算法的精度和实时性,并将算法应用到光储微网并网的实际研究中,以提高算法的实用性。

本文研究得到合肥工业大学应用科技成果培育计划重点项目(JZ2017YYPY0900)的资助,谨此致谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。