安全约束最优潮流的实用模型及故障态约束缩减方法

2018-07-12郭瑞鹏边麟龙宋少群余秀月

电力系统自动化 2018年13期

郭瑞鹏, 边麟龙, 宋少群, 余秀月, 汤　伟, 杨　铖

(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 国网福建电力调度控制中心, 福建省福州市 350003;3. 国网安徽电力调度控制中心, 安徽省合肥市 230022)

0　引言

电力系统安全运行应满足3类约束条件:①系统负荷需求;②运行约束(无潮流和电压越限);③可靠性约束(能承受一定预想故障的冲击)[1]。最优潮流以潮流方程为基础,进行经济与安全、有功与无功功率的全面优化,但仅考虑前2类约束,没有考虑可靠性约束。当某个电力设备发生故障并退出运行时,将引起潮流在电网中的重新分配,并可能导致部分电力设备潮流明显增大,若超过其短时过载能力,则可能在运行人员来不及干预的情况下发生连锁开断,给电网的安全运行带来严重威胁[2]。

由于电力系统故障的实时自动处理在技术上仍存在较大困难,故电网安全运行的着眼点在于预防事故后果。为避免预想开断引发连锁故障,给运行人员处理事故留出充足的时间,需要对电网正常运行时的潮流进行适当的控制,以保证可信的预想开断发生时不会引起电力设备潮流超过其短时允许载流量。安全约束最优潮流(security constrained optimal power flow,SCOPF)在最优潮流(OPF)模型的基础上,添加了可靠性约束,能够较好地保障电网的安全可靠运行。

对于大型电力系统,由于预想故障集的规模庞大,若对所有预想故障状态进行详细建模,并考虑其可靠性约束,则SCOPF问题的计算规模将非常庞大,其数值求解存在巨大困难,不具有实用价值。如何提高SCOPF问题的求解效率是其能否实用化的关键。Benders分解法[3-4]、并行计算技术[5]及专用稀疏矩阵处理技术[6]均被研究用于提高SCOPF问题的求解效率。文献[7-10]通过对预想故障集进行过滤,从而只考虑部分关键故障的可靠性约束,以减少预想故障集的规模。由于难以一次性给出准确的关键故障集,该方法一般需要通过循环进行多次关键故障集筛选,并进行多次针对关键故障集的SCOPF计算,其计算效率仍然较低。此外,若SCOPF问题最优解处起作用的故障集规模较大,则筛选后的关键故障集规模仍较大,SCOPF问题的求解效率可能很低,应用于大型电力系统仍存在巨大困难。文献[11]利用线路开断分布因子,将预想开断后的支路有功潮流描述为基态支路有功潮流的函数,建立了基于直流潮流法的SCOPF模型,并在算法实现中忽略了分布因子足够小的支路,提高了计算效率。但该方法完全忽略了有功损耗对电网运行经济性的影响,可能给优化结果带来较大偏差。

本文基于交流潮流模型建立基态约束条件,利用故障前后的有功潮流转移关系建立故障态约束条件,通过对并联线路或并列主变压器进行分组,减少需监视的支路规模,并利用设备短时通流能力大于长期通流能力的特征对故障态约束进行过滤,减小了SCOPF问题的计算规模。IEEE 14节点测试系统和华东电网的仿真分析验证了所提SCOPF模型及约束缩减方法的正确性和有效性。

1　基于潮流转移关系的SCOPF模型

1.1　目标函数

安全约束最优潮流一般以基态下机组总发电费用之和最小作为优化目标,即

(1)

1.2　基态约束

1)节点功率平衡约束

根据基尔霍夫电流定律,各节点有功及无功潮流均需保持平衡,即

(2)

(3)

2)机组出力约束

各机组有功及无功出力均应满足其上下限约束,即

(4)

3)节点电压约束

各节点电压幅值应满足其上下限约束,即

(5)

4)支路潮流约束

支路潮流约束实用中有2种描述方式:一种是支路电流不越限;另一种是支路有功潮流不越限。这里采用第2种。根据支路允许电流或容量计算有功功率上限时一般取一定的保守系数,如0.95。

(6)

式中:SB为支路集合。

支路基态有功潮流允许范围约束可描述如下:

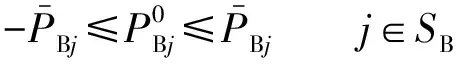
(7)

式(6)和式(7)给出了支路始端流向末端的有功潮流约束。理论上还应该考虑支路末端流向始端的有功潮流约束。考虑到与设备长期允许载流量相比,支路有功损耗一般足够小,故支路始端有功潮流不越限,支路末端有功潮流在误差许可范围内可以认为不会越限,故实用中可以仅添加支路始端的有功潮流约束以减小计算规模。

5)暂态稳定断面功率极限区间约束

输电断面作为功率输送的通道和电气联系的走廊,集中体现了电网中的薄弱环节,当传送功率过大时,可能存在安全稳定隐患。实用中,电网调度运行人员需要通过暂态安全稳定时域仿真计算确定输电断面暂态稳定极限功率区间[12-13]。

暂态稳定断面功率极限区间约束可描述为:

(8)

1.3　故障态约束

电力系统安全运行的可靠性约束要求电网能够承受一定预想故障的冲击,即预想故障发生导致部分电力设备退出运行时,任意电力设备的潮流均不超过其短时过载能力,以避免发生连锁开断,给运行人员处理故障留出充足的时间。

预想故障集的选择实用中一般采用N-1安全准则,主要考虑线路N-1故障、主变压器N-1故障及母线N-1故障。机组N-1故障的后果与相应升压变压器N-1故障的后果基本相当,实用中可以忽略。

高压电网中,支路有功潮流间具有较好的线性关系,方便建立预想故障前后支路有功潮流间的联系。根据文献[14],预想故障k发生后,支路j的故障态有功潮流可描述为其基态有功潮流及所开断各支路基态有功潮流的线性函数,即

(9)

潮流转移关系的计算可以采用交流潮流法[14]或直流潮流法[15]。文献[16]较为详细地介绍了潮流转移比的概念及计算方法,并给出了适用于大规模电力系统潮流转移比计算的多核并行批处理方法。潮流转移关系则是根据潮流转移比将故障后支路有功潮流描述为故障前支路有功潮流的线性函数。

在OPF模型的基础上添加考虑N-1安全准则的可靠性约束,即

(10)

SCOPF模型在OPF模型的基础上添加了式(9)及式(10)的可靠性约束,将导致发电成本升高,但优化结果能够满足静态安全校核要求,即预想故障发生后各电力设备的有功潮流均不会超过其短时过载能力,为事故处理留出足够的时间。

潮流转移关系的计算精度对SCOPF的计算结果有一定影响。对于实际输电网,由于支路的R/X比值较小,采用直流潮流法或交流潮流法计算潮流转移关系一般能够满足工程应用要求。对于精度要求较高的场合,可以添加外循环,在SCOPF结果处采用交流潮流法更新潮流转移关系,并重新进行SCOPF计算,直至满足期望的计算精度要求。

2　SCOPF模型缩减方法

由式(1)至式(10)构成的SCOPF模型的计算规模巨大,其数值求解的计算效率难以满足实际大电网的应用要求。

2.1　监视支路选择

不论是基态,还是故障态,对于并联线路或并列主变压器,其有功潮流的分配比例近似为常数。对于并联线路,各线路的有功潮流分配比例主要由其阻抗决定,两条参数相同的线路并联,各线路上流过的有功潮流必定相同。对于并列主变压器,以图1所示的两台500 kV并列主变压器为例加以说明。典型的,主变压器低压侧仅连接并联补偿设备,故低压绕组的有功潮流恒为0。若忽略主变压器损耗,则任一主变压器高压绕组的有功潮流等于中压绕组的有功潮流,两台主变压器的有功潮流分配比例主要由其高、中压绕组的阻抗之和决定。

图1　500 kV并列主变压器结构Fig.1　Structure of parallel 500 kV transformers

将并联线路或并列主变压器划分为组。定义流入设备组的有功潮流之和为设备组有功潮流,定义支路有功潮流占设备组有功潮流的比例为分支系数,即

(11)

由于分支系数近似为常数,与具体的运行状态关系不大,故可以根据基态潮流确定。

由于同一设备组内各支路的有功潮流分配比例近似为常数,故每个设备组中仅需对分支系数与允许载流量比值最大的支路进行监视。

对于基态支路潮流约束,可根据式(12)选择需监视的支路。

(12)

将基态支路有功潮流描述为监视支路有功潮流的函数,则有

(13)

式中:Mj为支路j所属设备组的基态监视支路编号。

对于故障态支路潮流约束,可根据式(14)选择需监视的支路。

(14)

根据式(12)或式(14)选择的监视支路是设备组在相应运行状态中最容易越限的支路。若该支路有功潮流不越限,则该设备组中所有支路的有功潮流都不会越限。

根据上述分析,式(6)、式(7)、式(9)及式(10)可替换为:

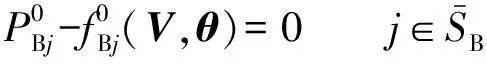
(15)

(16)

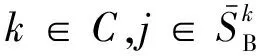
(17)

(18)

通过监视支路选择,式(15)及式(16)仅添加各监视支路的基态有功潮流变量及相应的上下限约束,式(17)及式(18)也仅对监视支路添加潮流转移关系及故障态潮流约束。典型的,500 kV变电站的目标规模为3台主变压器并列运行,9条支路中仅需选择1条监视支路,故实际电网中所选择的监视支路数远小于所有支路数。监视支路选择有助于显著减小SCOPF问题的计算规模。

此外,式(17)事实上是将式(9)中各支路基态有功潮流的线性函数变换为各设备组中监视支路基态有功潮流的线性函数。由于式(9)中的相关支路可能属于同一设备组,可以合并同类项,故式(17)比式(9)具有更好的稀疏性,有助于提高SCOPF问题的求解效率。

2.2　故障态约束过滤

SCOPF问题中故障态约束条件的数目非常可观,给其数值求解带来了巨大困难,如何减少故障态约束条件是SCOPF模型能否实用化的关键。对于实际电力系统,预想故障的影响范围一般较为有限,故可以仅对故障影响域内的设备进行监视[17]。

电力线路及变压器一般具有一定的承受短时功率冲击的能力,故短时允许载流量明显大于其长期允许载流量。架空线路的短时过载倍数一般大于1.3,新投运主变压器的短时过载倍数甚至高达1.8以上。实用中,可以利用短时过载倍数大于1的特点对故障态约束进行过滤。

由式(16)及式(17)可得:

(19)

记

(20)

若

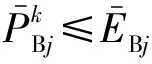
(21)

则式(18)中对应的不等式约束必定成立,即相应的约束为冗余约束,对优化结果没有影响。

式(20)及式(21)中的参数均可以在优化计算前得到,故可以用于对故障态支路潮流约束进行筛选,只将可能起作用的约束加入优化模型中,从而大大减小SCOPF问题的计算规模,提高数值求解效率。

3　算例分析

本文提出的SCOPF模型数学上为非线性规划问题,可以采用非线性规划原对偶内点法求解。原对偶内点法的介绍见文献[18],这里不再赘述。

基于本文所提出的模型及约束缩减方法,采用C++语言开发了电力系统SCOPF软件,并用于对IEEE 14节点测试系统及华东电网进行仿真测试。仿真环境为Microsoft Visual Studio 2015,计算机硬件配置为Intel(R) Core(TM) i7-7700HQ CPU@2.81 GHz,16 GB内存。仿真中,原对偶内点法的向心参数取0.3,IEEE测试算例的精度要求取为1.0-8,华东电网测试算例的精度取1.0-6,预想故障开断平衡机时根据电压等级最高、容量最大的原则选择新平衡机。

3.1　IEEE 14节点测试系统

IEEE 14节点测试系统的拓扑结构如图2所示。对于图2中采用虚线表示的线路,其长期允许载流量设为100 MVA,其余支路的长期允许载流量均设为50 MVA。测试中,各节点的电压允许运行区间均取为0.94～1.06(标幺值),支路短时允许载流量设为长期允许载流量的1.3倍,取支路容量的95%作为有功潮流限值。发电机的成本曲线采用二次函数描述,其参数如表1所示。

图2　IEEE 14节点测试系统拓扑Fig.2　Topology of IEEE 14-bus test system

节点有功下限/MW有功上限/MW无功下限/Mvar无功上限/Mvar成本曲线常数项/美元一次项/(美元·(MW·h)-1)二次项/(美元·(MW·h)-2) 103000100100.043 20150-40500200.250 301000400400.010 60100-6240400.010 80100-6240400.010

由图2可以看出,IEEE 14节点测试系统的并联支路较少,仅节点1-2之间存在2条并联线路。由于这2条支路的参数完全相同,故其分支系数均为0.5,且这2条支路中任一条支路不越限,则另一条支路也不会越限,故可任选其中一条支路进行监视,这事实上是根据式(12)或式(14)选择监视支路的特例。

为帮助理解故障态约束过滤过程,表2给出了节点2母线故障时采用直流法求解得到的部分潮流转移关系及约束过滤说明。表中,Pmn表示支路m-n的节点m侧流入支路的基态有功潮流。

表2　IEEE 14节点测试系统潮流转移关系及约束过滤Table 2　Power transfer relations and constraints filtering on IEEE 14-bus test system

考虑到IEEE 14节点测试系统中线路的R/X比值较大(支路12-13的比值约为1.1),与输电网中线路R/X比值较小的特征不符,对IEEE 14节点测试系统中各支路的电阻均乘以0.2,构成IEEE 14节点修正系统。表3给出了IEEE 14节点测试系统及IEEE 14节点修正系统的SCOPF仿真计算结果。表中,TACSCOPF表示传统的交流SCOPF[7],即直接采用故障态交流潮流约束描述的SCOPF,在本文中作为SCOPF问题的精确解;UDCTRSCOPF表示采用直流潮流法计算潮流转移关系,并采用系数0.01对潮流转移比进行过滤的SCOPF;DCTRSCOPF表示采用直流潮流法计算潮流转移关系,并采用本文方法进行约束缩减的SCOPF;ACTRSCOPF表示采用交流潮流法计算潮流转移关系,并采用本文方法进行约束缩减的SCOPF,后缀的数字表示外循环迭代次数;转移关系数表示本次SCOPF计算时未被过滤掉的,参与SCOPF计算的转移关系数量。

表3　IEEE 14节点测试系统及IEEE 14节点修正系统仿真计算结果Table 3　Simulation results of IEEE 14-bus test system and IEEE 14-bus modified system

比较表3第3,4行可以看出,UDCTRSCOPF和DCTRSCOPF的目标函数值偏差极小,由此说明约束过滤对优化结果几乎没有影响。

由表3第2,3,5列可以看出:①UDCTRSCOPF平均每个预想故障包含约15条潮流转移关系约束,与IEEE 14节点测试系统的支路数21相比,参与优化计算的比例约为71%;②采用本文约束缩减方法,DCTRSCOPF及各ACTRSCOPF中平均每个预想故障包含约5条潮流转移关系约束,参与优化计算的比例约为24%(由于IEEE 14节点测试系统中并联线路及并列主变压器较少,仅节点1-2之间存在2条并联支路,该比例相对较大,实际系统参与优化的约束比例要小得多)。

由表3第1,4,6列可以看出,采用同样的SCOPF模型,IEEE 14节点测试系统的偏差明显大于IEEE 14节点修正系统,其原因在于IEEE 14节点测试系统的R/X比值较大,有功损耗的非线性导致潮流转移关系的近似误差较大。

比较表3第2,6,7行可以看出:对ACTRSCOPF引入外循环,有助于提高SCOPF问题的求解精度。即使对IEEE 14节点测试系统这样一个R/X比值较大的系统,进行2到3次外循环就能够达到较高的计算精度,能够满足工程应用要求。

3.2　华东电网仿真测试

为了测试本文所提SCOPF模型的求解效率及约束过滤效果,对华东电网2017年夏季高峰运行方式进行了仿真测试。

该方式下华东电网共有6 355个节点和10 108条支路。采用本文2.1节提出的监视支路选择方法能够将支路划分为4 529个设备组,故只需对4 529条支路进行监视,能够有效减小SCOPF问题的计算规模。

测试中考虑2种典型应用场景:①华东电网应用场景,优化范围为500 kV电厂,监视支路为500 kV及以上的线路及主变压器,故障集包括500 kV及以上线路及主变压器N-1故障;②省级电网应用场景,优化范围为省内220 kV及以上电厂,监视支路为省内220 kV及以上线路及主变压器,故障集包括省内220 kV及以上线路及主变压器N-1故障,以及220 kV母线N-1故障。附录A表A1给出了2种典型场景下华东电网SCOPF的仿真计算结果。

对2种典型应用场景下的各算例,由附录A表A1可以得到以下结论。

1)DCTRSCOPF和UDCTRSCOPF的目标函数值偏差极小,约束缩减对优化结果几乎没有影响,但能够明显缩小计算规模,在计算速度上的优势明显。

2)DCTRSCOPF给出的目标函数值与ACTRSCOPF3的偏差均小于2%,可以适用于精度要求不太高的场合。

3)ACTRSCOPF2给出的目标函数值与ACTRSCOPF3的偏差均小于0.1%,对ACTRSCOPF引入外循环迭代的收敛速度快,2～3次迭代就能够达到很高的收敛精度。

4)TACSCOPF优化成功的情况下,目标函数值与ACTRSCOPF3的偏差均小于0.5%,说明潮流转移关系约束能够较好地描述故障后支路有功潮流约束。

5)预想故障集规模较大时,TACSCOPF的计算规模巨大、计算时间长、占用内存空间大,难以满足实际大电网的应用要求。

6)单次DCTRSCOPF或ACTRSCOPF的计算时间均为秒级,其计算效率能够满足实际大区电网或省级电网的应用要求。