基于CES型效用函数的热—电市场消费者最优决策

陈　玥, 魏　韡, 刘　锋, 梅生伟, 袁铁江

(1. 清华大学电机工程与应用电子技术系, 北京市 100084; 2. 电力系统及发电设备控制和仿真国家重点实验室, 清华大学, 北京市 100084; 3. 大连理工大学电气工程学院, 辽宁省大连市 116024)

0　引言

随着经济的发展,国际社会面临着能源短缺和环境污染的双重压力。据统计,2014年中国能源消费总量为42.6亿吨标准煤,比去年同期增长2.2%,其中煤炭消费占比高达66%。为应对强烈依赖一次能源的消费结构带来的系列问题,多能源综合利用得到了广泛关注。能量转换设备如热电联产(CHP)机组等发展迅猛,各能源网络耦合日益密切[1-2]。

多能源网络融合给能源系统运行带来了新的机遇与挑战,多能源协同优化被视为提高系统调峰能力、促进可再生能源消纳的途径之一[3],相关研究方兴未艾。文献[4-5]总结了多能互补网络建模、优化和演化机理研究等方面的关键技术,并对其前景进行了展望。在系统运行方面,利用能量中心对多能耦合特性进行建模是常见思路之一[6-7]。文献[8]基于能源中心的建模方法研究了气—热—电系统的稳态潮流分布,文献[9]对该模型进行了改进,使之更具有通用性。文献[10]研究了含储热光热电站的电网调度及其并网效益。文献[11]提出了电热系统中热网潮流的前推回代算法,为多能仿真提供了技术手段。文献[12]研究了含碳捕捉电转气设备的气—热—电系统优化运行。多能源系统还被用于应对可再生能源及负荷不确定性[13-15]。文献[16]验证了储能设备可以有效解耦热电运行约束,降低运行成本。

除系统运行外,多能源市场亦得到广泛关注。文献[17]探讨了冷热电联供系统并网的电价体系及基本电价计算方法。文献[18]讨论了市场环境下的CHP机组和热储备之间的短期联合经济运行。文献[19]基于粒子群算法给出了含热—气—电机组的最优定价。文献[20-21]研究了考虑价格及负荷不确定性的能量中心管理者最佳定价问题。

上述研究均假设多能源市场在同一个集体利益最大化目标下运行。然而在现实中,不同能源网络由不同主体运营,各主体之间的利益互相冲突,每个主体决策行为的目标是实现自身利益最优。在此背景下,分析多能源系统能量交易中的趋利行为、主体间博弈关系及其对市场均衡的影响具有重要意义。针对此问题,文献[22]提出了一套工程实用化的博弈分析方法。文献[23]对燃气三联供和热泵最佳匹配容量进行可视化分析,为各能源公司趋优决策提供更为详尽的信息。文献[24]基于Nash博弈理论给出含电转气(P2G)设备的多能源市场均衡。文献[25-26]构建了多能源系统Stackelberg博弈模型。文献[27]研究了气—热—电系统间的替代和竞争关系对市场价格的作用。但该模型只考虑了电力市场出清,而燃气、热力系统采用了简单的竞价策略,且未考虑多能源消费者的选择决策。

本文研究了基于常数替代弹性(CES)效用函数的热电市场消费者决策问题,所提研究方法较已有成果有以下不同:首先,在本文的热电交易框架中,热力系统与电力系统处于对等地位,二者同时出清得交易价格;其次,消费者不再只是价格的接受者,而可以调整消费量影响能源价格。利用CES效用函数可以探究一系列具有不同替代弹性消费者的市场行为。最重要的是,在市场均衡处,电网、热网和消费者三方的利益均达到最优,任何一方无法通过单方面改变自身策略获利。总之,本文方法可以预测消费者行为调整及其对能源价格的影响。

1　热电市场交易机制描述

本文所研究的热电市场消费者决策问题构成双层Stackelberg-Nash博弈:其中,消费者与热—电市场之间存在Stackelberg博弈;热力市场和电力市场之间存在Nash博弈。在市场均衡处,任何一方无法通过单方面改变自身策略获利,说明该市场均衡即为Stackelberg-Nash博弈均衡。该热电市场交易模式及决策次序如图1所示。该市场由能源市场1(电力市场)、能源市场2(热力市场)和消费者构成。各主体单独决策实现各自目标最优化,主体间存在博弈关系。其中,发电商的成本视为给定值,即不考虑发电商报价行为。市场交易分为三个阶段。

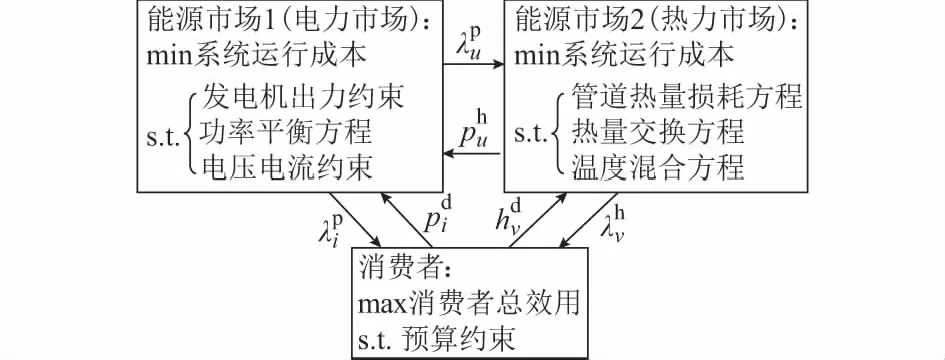
图1　热电市场交易模式机制Fig.1　Trading mode mechanism in heat-power market

2　消费者决策问题

在本节中,通过对各市场主体及相互间耦合关系进行建模,刻画市场主体间博弈关系。具体来说:首先给出基于CES型效用函数的消费者决策模型,在模型中,电价和热价作为常量;接着对电力市场和热力市场进行刻画,并给出出清电价和热价。

2.1　基于CES型效用函数的消费者决策模型

效用函数通常用来表示消费者在消费中所获得的效用与所消费的商品组合之间的关系,以衡量消费者从既定的商品组合中所获得满足的程度。消费者决策问题的目标是最大化消费者效用,如式(1)所示。此处选择一种经典的效用函数形式——CES效用函数[29]。该效用函数表征一类替代弹性为常数的效用函数,且当与替代弹性值相关的参数ρ→0时,CES效用函数退化为Cobb-Douglas效用函数;当ρ=1时,为完全替代型效用函数;当ρ→∞时,表征完全互补型效用函数。利用CES效用函数,可以分析这些特例和其他介于特例之间的情况,是分析不同消费者效用类型影响的重要工具。消费者的决策问题是在预算约束下分配电量和热量消费,使得消费带来的效用最大化。具体表述为:

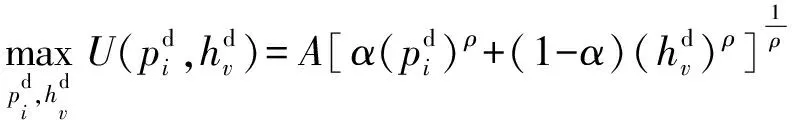
(1)

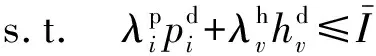
(2)

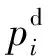
2.2　电力市场出清模型

电力系统节点电价可由最优潮流模型的对偶变量得到[30]。当电力系统满足一定条件,如线路两端相角足够小、线路电抗远大于电阻、电压幅值接近于额定值等时,最优潮流常通过一系列近似而转化为直流最优潮流模型,该模型为一类典型的线性优化问题。由于热网通常接入配电网,配电网线路电阻和网损较大,需要采用交流潮流模型才能保证节点电价的精确度。本文采用文献[31]提出的放射状电网支路模型,目标为最小化自身成本,如下式所示:

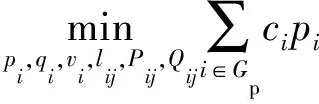
(3)

式中:pi,qi,vi,lij,Pij,Qij为决策变量,其中pi和qi分别为电力系统有功和无功出力,vi为节点i电压平方值,lij为线路i-j电流平方值,Pij和Qij分别为线路i-j有功和无功功率；ci为发电机组单位有功出力成本;Gp为发电机节点集合;。

相关约束如下。

1)支路潮流方程

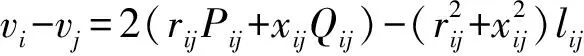
(4)

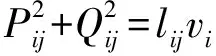
(5)

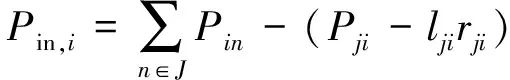
(6)

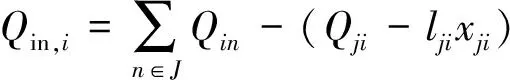
(7)

(8)

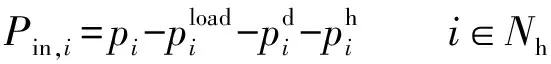
(9)

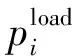
2)变量范围约束

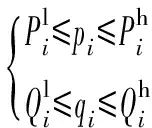
(10)

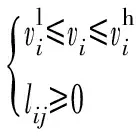
(11)

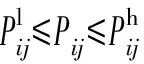
(12)

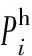
上述二次等式约束(式(5))使问题(式(3)至式(12))成为一个非凸非线性优化问题。利用二阶锥松弛(SOCR)法可以对上述问题进行求解。首先将约束式(5)松弛为下述二阶锥约束:

(13)

接着对松弛后的问题进行求解,以期得到原问题的一个最优解。文献[32]的研究表明,对辐射状电网SOCR一般是精确的。

本文进一步利用多面体近似方法[33]将式(13)线性化,便于列写电力市场出清问题的最优性条件。具体来说,首先将式(13)等价拆分为下述约束:

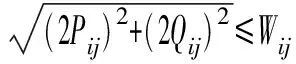
(14)

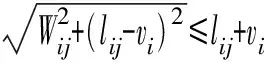
(15)

(16)

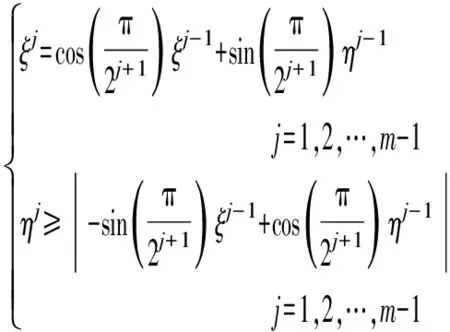
(17)

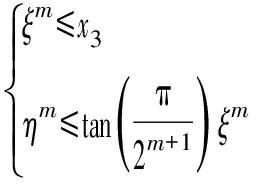
(18)

式中:ξj和ηj(j=1,2,…,m)为辅助变量,其中m为近似采用的分段数。

从而可得电力市场出清问题的线性规划描述,简记为:

(19)

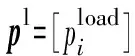
2.3　热力市场出清模型

常见的热力网络如附录A图A1所示,由供水管道和回水管道构成。供水管道温度高,回水管道温度低。经过热源时,传热工质(水)被加热进入供水管道;经过热负荷时,管道中热水释放热量后通过回水管道流回热源。本文采用固定质量流量(CF-VT)的运行模式[34],即保持管道质量流量,通过改变供热网络的供水温度来满足热负荷的供应。在CF-VT模式下,循环水流量、压强水头分布等都为定值,此时热力系统可以建模成一个线性规划模型[35]。其目标为最小化自身成本,如下式所示:

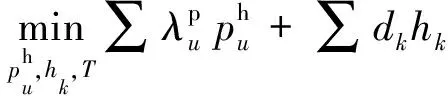
(20)

相关约束如下。

1)购电量和产热量限制

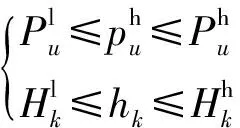
(21)

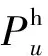
2)管道热量损失

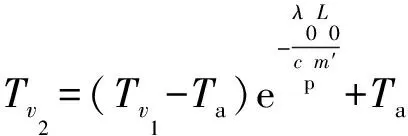
(22)

热量损失体现为管道首端水温Tv1与末端水温Tv2差异,热量损失与水的比热容cp、管道长度L0、水量m′、环境温度Ta以及单位管道长度热传输系数λ0相关。

3)热量交换约束

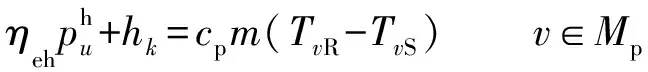
(23)

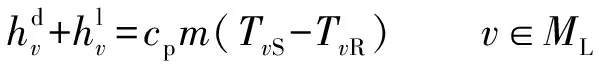
(24)

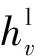
对于热源,外部输入的热量体现为管道水温的上升;对于热负荷,其吸收的热量体现为管道水温的下降。

4)汇流节点温度混合方程

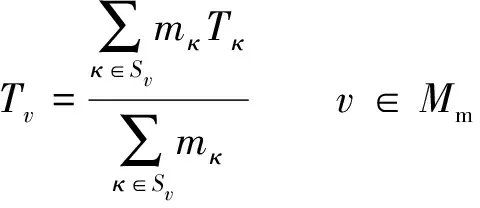
(25)

式中:Sv为入流管道集合;Mm为含多入流管道节点集合。

根据能量守恒定律,来自不同管道的水流在同一网络节点混合后的温度满足上述方程。

上述热力市场线性出清问题可简记为:

(26)

消费者、电力市场、热力市场间存在Stackelberg-Nash博弈。消费者决策问题(式(1)和式(2)),电力市场出清问题(式(3)至式(12))和热力市场出清问题(式(20)至式(25))构成双层规划问题,其中上层问题为消费者决策问题,下层问题为市场出清问题。下面将基于KKT(Karush-Kuhn-Tucker)条件和对偶理论给出热电市场均衡的混合整数线性约束条件,并利用MATLAB全局优化工具包中的模式搜索函数(patternsearch)求解消费者的最优申报策略。

3　求解方法

上述双层规划问题中,热电耦合体现在:一方面,在能源市场出清问题中,热力系统可以向电力系统购电用来产热,此行为既会影响电网负荷量又会影响热网运行成本,从而形成复杂的耦合关系;另一方面,在消费者决策中,购电量和购热量受到预算约束的限制,用户在电、热之间进行取舍,以最大化其效用,电/热购买量存在耦合关系。

3.1　电力系统问题的原对偶转化

对于电力市场出清问题,热力系统和消费者的购买电量是给定的,若将线性规划(式(19))用其原对偶条件代替,即可消去优化目标,得到最优解处变量{p,z}、对偶变量{μ,λp}与消费电量{pD,ph}之间的关系:

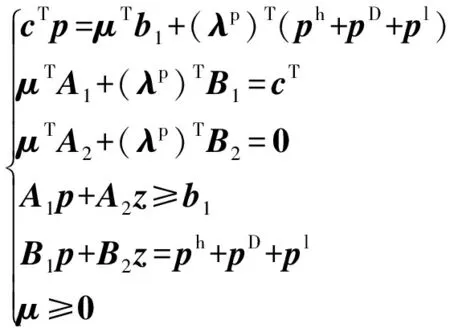
(27)

3.2　热力系统问题的KKT转化

对于热力市场出清问题,电价和消费者购买热量是给定的,若将线性规划(式(26))用其KKT条件代替,即可消去优化目标,得到变量{h,ph},对偶变量{η,λh,ρ}与电价{γ}、消费者购买热量{hD}的关系:

(28)

式中最后一个约束方程为互补松弛条件,其中x⊥y表示向量x与y中至多有一个可以严格大于0。采用文献[36]中的方法,通过引入布尔变量可将互补松弛约束转化为以下线性不等式:

0≤η≤Mθ

(29)

0≤A3h+A4ph-b2≤M(1-θ)

(30)

式中:M为足够大的常向量;θ为由0-1变量构成的向量。

3.3　市场出清条件线性化

电力市场出清条件(式(27))和热力市场出清条件(式(28)至式(30))构成热电市场出清条件,该条件中的非线性源于电价和购买电量的乘积(λp)Tph。线性规划的对偶定理表明,在最优解处原问题和对偶问题的目标函数值相等。对于线性规划式,可得如下等式:

ηTb2+ρTb3+(λh)T(hD+hl)=dTh+γTph

(31)

将式(31)代入式(27),可以消去非线性项得到线性化的热—电市场出清条件,记为f=φ(x),其中f为出清价格,x为消费者消费量,φ为函数映射关系。

3.4　消费者决策问题求解

经过上述转化,得到线性化的热—电市场出清条件,将其作为约束代入消费者决策问题(式(1)和式(2))中,作为外生参数(电价/热价)的确定条件,该问题可表示为:

maxg(x)

(32)

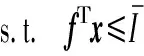
(33)

f=φ(x)

(34)

上述优化问题中,约束条件式(33)是消费者预算约束,反映了热、电消费量之间的耦合关系;约束条件式(34)代表热—电市场出清条件。在上述对热—电市场问题的等效处理中,虽然分别对电力系统问题和热力系统进行原对偶和KKT转化,但二者之间的耦合关系依然存在。具体表现为:电力系统等效原对偶条件(式(27))中常数项ph为热力系统KKT条件式(28)中的决策变量;而式(27)中的对偶决策变量λp中分量γ为式(28)中的常数项。将两个市场的等效出清条件进行联立时,耦合关系会导致存在非线性项(λp)Tph,通过条件式(13)对该项进行替代,进而得到考虑热电市场耦合特性的线性市场出清条件。

利用MATLAB中的patternsearch函数可对该问题进行搜索求解。其基本原理是将x的可行域离散化为一系列网格点,计算网格点处的目标函数值,并根据计算结果更新网格点,将最优解可能出现的区域细化,直到搜索误差小于给定值。利用模式搜索求解优化问题(式(32)至式(34))的基本流程如附录A图A2所示。

根据上述算法所得结果,为Stackelberg-Nash博弈的均衡解,满足各方利益最优化,即任何一方无法单方面通过改变自身策略而获益。

4　算例分析

本节通过算例说明前文所提模型和求解方法的有效性。同时分析了不同消费者偏好类型、预算、效用函数等因素对消费者决策和市场价格的影响。

4.1　系统配置

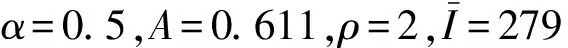
4.2　标称系统最优解

在标称场景下,利用模式搜索求解消费者热电市场决策问题,得到的结果如下:电力系统总成本为150 468. 84元,热力系统总成本为52 119.92元,消费者购买电量为194 kW,热量为167.5 kJ,接入电网处的节点电价为0.725元/(kW·h),接入热网处的节点热价为0.825元/kJ,消费者效用为110.81元。各发电机出力如附录C表C1所示。

为反映网损对配网市场出清价格的影响,图2中给出了直流潮流和交流潮流下的电力系统不同节点的电价。该对照组直流潮流模型如下式所示:

(35)

(36)

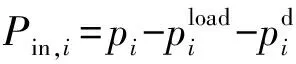
(37)

(38)

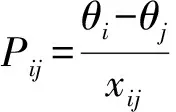
(39)

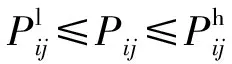
(40)

式中:θi为节点相位。

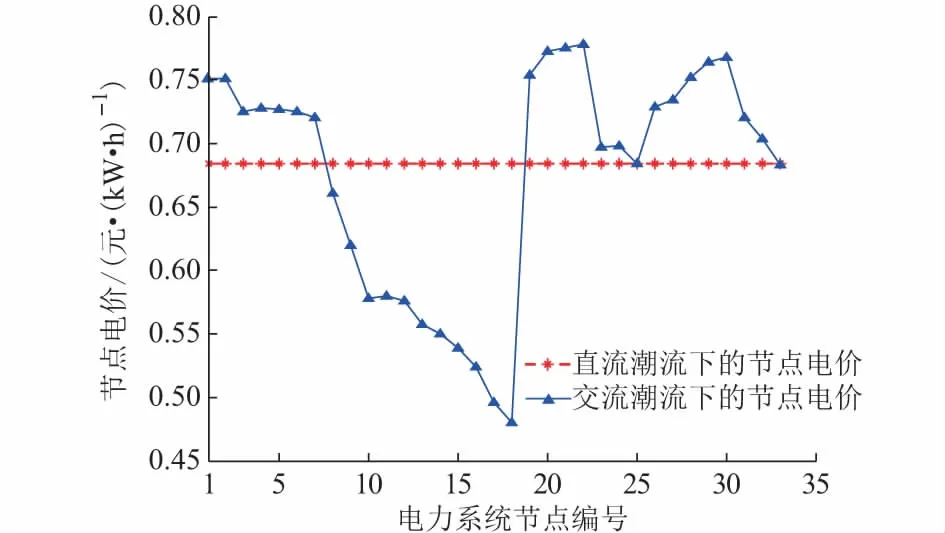
图2　电力系统节点电价Fig.2　Locational marginal price in power system

与文中交流潮流模型相比,对照组直流潮流模型考虑了有功出力范围约束(式(36))、节点功率注入约束(式(37))、功率平衡约束(式(38))和传输线功率约束(式(39)和式(40)),但忽略了网损,其中节点注入功率平衡方程(式(37))的对偶变量λi即为节点电价。

从图2中可以看到,在直流潮流下,由于忽略了网损,在线路不存在阻塞的情况下,各节点电价一致,等于电网中出力没有达到边界的那台机组的边际成本;在交流潮流下,考虑了线路网损,各节点电价不同。同时可以看到,发电机节点处电价较低,随着与发电机距离的增加,节点电价增加。这是因为线损随传输距离增加而增加,导致节点电价上升。该差异表明由于配电网线路阻性明显,故在计算节点电价时采用交流潮流模型能够提高准确度,而采用直流潮流可能造成较大误差。

4.3　消费者偏好对最优解的影响

在消费者效用函数中,参数α表征对电和热的偏好,α的值越大表明越偏好消费电。分别取α=0.1,0.3,0.5,0.7,0.9,标记为A至E类型消费者,则从A到E类型,消费者对电的偏好越来越大。在其他参数保持不变的基础上求解消费者热电市场决策问题,得到的消费者购买量和效用变化如图3所示,市场电价/热价变化如附录C图C1所示。

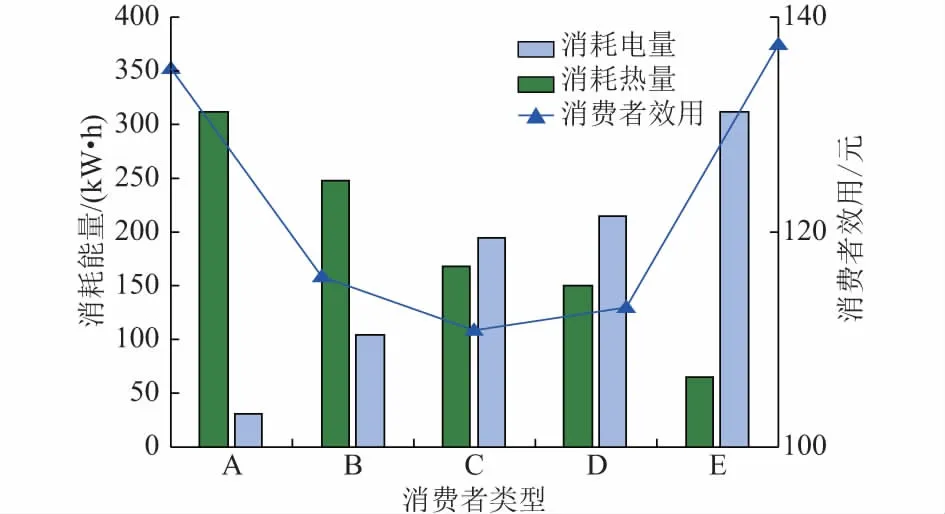
图3　不同偏好下消费量及效用变化Fig.3　Energy consumption and utility under different preferences

从图3中可见,随着对电偏好的增加,电量消费增加,热量消费减少。同时可以观察到,消费者的效用先减后增。这说明在给定的预算下,一个平均偏好的消费者效用更低。换言之,若消费者倾向于高效用,则应倾向于使用某一种能源。附录C图C1中显示,节点电价基本不变,节点热价逐渐降低。这是因为,消费者消费的电量对于电力系统整体容量而言比较小,所以对电价影响不大。而随着对电偏好的增加,消耗热量减少,热力系统成本下降,因此热价逐渐下降。

4.4　消费者预算对最优解的影响

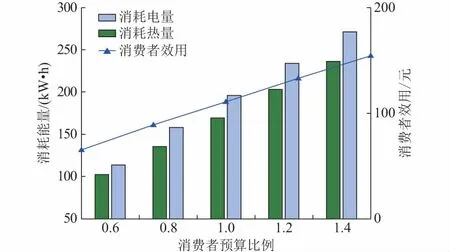
图4　不同预算下消费量及效用变化Fig.4　Energy consumption and utility under different budgets

从图4中可以看出,随着预算的增加,消费者消费的电量和热量都有所上升,但前者增长较快；效用也逐渐增加。这是因为,在预算增加的同时,消耗电量和热量增加会导致节点电价和热价上升,而受到预算的限制,价格的上升会抵消部分电量和热量的上升趋势,所以消费量的增长略缓于预算增长。同时可以观察到,由于消费者具有边际效用递减的特点,其效用变化曲线为上凸,即增长趋势逐渐变缓。

附录C图C2中显示,电价和热价先缓慢增长后加速增长。这是因为,随着能源消费量的增加,系统趋向于饱和,所以消费量的进一步增加对系统运行成本的冲击较大,能源价格也就较高。

4.5　消费者效用函数形式对最优解的影响

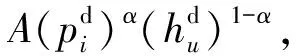
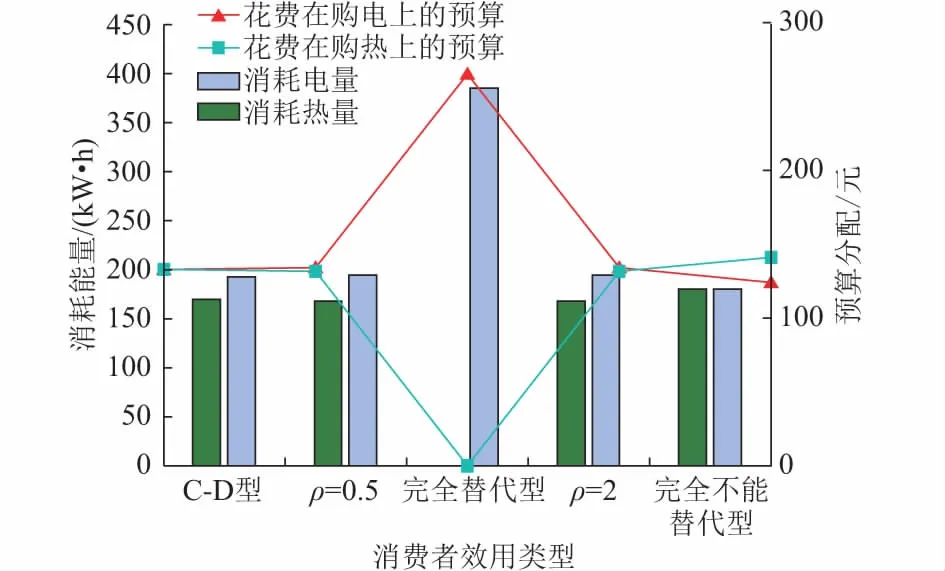
图5　不同效用函数形式下消费量及预算分配变化Fig.5　Energy consumption and budget allocation under different utility functions

由图5可知,ρ=1时,只消耗电量不消耗热量。这是因为,此时的电价低于热价,而二者是完全可替代的,所以消费者会选择只购买价格低者来最大化效用。在ρ→∞时,即完全互补情况下,由于短板效应,只有当两种能源消费量相等时,消费者效用才最大。当ρ=0.5, 2时,能源消费情况相同。当为Cobb-Douglas型效用函数时,效用最大化下花费于购买电量和购买热量的预算相等。

5　结语

多能源网络耦合已成为未来能源系统发展的必然趋势之一,多能源交易及其市场均衡分析是重要的研究课题。本文提出了考虑CES型效用函数的热电市场消费者决策模型,刻画了消费者、热力市场、电力市场三者之间的博弈关系。为得到市场均衡,本文首先通过KKT条件和线性规划对偶定理得到混合整数线性市场出清条件,进而利用模式搜索方法求解消费者最优策略。算例验证了本文所提方法的有效性。计算结果表明:①均衡偏好型消费者从多能源消费中获得的效用最低;②消费者预算的增加会导致能源消费量、效用和能源价格的上升;③具有不同效用函数形式消费者决策行为具有较大差异:Cobb-Douglas型消费者倾向于将预算均分用于购电和购热;完全替代型消费者选择二者间价格较低者购买;完全不能替代型消费者电量和热量消费相等。

需要说明的是,本文虽然仅针对具有CES型效用函数的热—电市场消费者决策问题进行建模,但该框架及算法具有良好的拓展性,可为多能源接入市场、多主体参与市场的博弈均衡分析提供有益的参考。未来可能的研究方向包括:市场博弈均衡的性质研究(存在性、稳定性分析),以及新交易模式对多能源市场均衡影响探讨等。

本文受国家自然科学基金项目(U1766203,51577163)资助,特此感谢。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。