基于非零和博弈的互联系统协同消纳风电调度法
2018-07-12霍启敬孙志攀
栗 然, 霍启敬, 陈 宇, 孙志攀
(华北电力大学电气与电子工程学院, 河北省保定市 071003)
0 引言
能源是现代社会赖以生存和发展的基础,为了应对能源危机,如何使可再生能源在人类生产、生活中得到充分有效的利用,成为当今研究领域备受关注的问题。与调峰电源丰富的发达国家电源结构明显不同, 中国电源结构以火电为主,大规模风电并网将使电网面临发电侧备用资源缺乏, 导致系统调峰容量严重不足,弃风电量高居不下等问题[1]。因此,迫切需要调动更广泛的备用资源参与含风电系统的调度运行管理。
随着电力系统的发展和扩大,各个孤立电力系统通过联络线联合成为互联电力系统已成为必然趋势。文献[2]通过论述电网的输电能力、风电并网后调度运行水平等不同角度下的影响风电消纳关键因素,提出了加强跨区域电网建设力度等关键措施。文献[3]进一步指出,在电网结构未有大的改善之前,需要依靠科学合理的调度模式和原则才能保障风电的稳定多发。文献[4]利用不同区域风功率互补的特点,提一种多级协调调度模式,统一协调多个区域的备用和调峰安排,从而达到充分消纳风电的目的。在此基础上文献[5]站在风险评估的角度提出基于目标级联分析的分散协调风险调度方法,保留各个子系统自治性的同时经上级调度进一步优化联络线上功率,实现大环境经济运行。但由于上下层优化目标不同,难以实现全局最优。并且在实际互联电力系统中,各区域系统数据相互保密,上层优化困难,因此文献[6-7]在子系统的边界设置一些虚拟节点,使多个子系统进行虚拟节点信息的交换,从而实现解耦。
能源互联网(Energy Internet)概念[8-10]的提出,以及第三次工业革命使能源互联网内可再生能源具有分散性的特点,必须采取协作模式,而非集中式或分级指挥和控制机制实现互联,“分散自制,集中协同”成为电网调度控制的新理念。而通过分析上述文献的联络线调度计划目标函数发现,参与的多个区域均被视为一个经济利益共同体,在不考虑自身利益的前提下参与优化调度。该目标函数下的最优解由于只注重整体效益,容易出现效益分配不合理甚至导致部分区域出现利益牺牲。
实际区域往往倾向于从个体经济利益出发,追求共赢,因此本文提出一种区域间通过非零和博弈协调消纳风电的联络线优化调度模式,求出以纳什均衡点存在的最优解集,在追求社会经济效益最大化的前提下以进一步分配的形式共享所创造的利益,从而提高风电消纳区接收外送功率的积极性。同时,本文采用帕累托最优聚点均衡的分析方法,进一步找出多重均衡下的谢林点,实现保证互联系统鲁棒性的同时提高互联系统的经济性。
1 参与区域博弈模型的建立
1.1 博弈因子

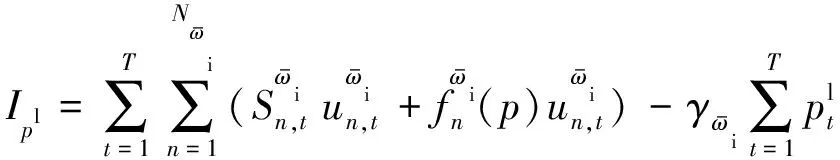
(1)

(2)


(3)
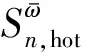


(4)
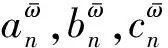
为了进一步简化模型,本文只考虑具有代表性的风电高发区与风电协助消纳区两个区域,为二人博弈局面。实际的互联电网是多方的,为多人博弈,从而会形成多维博弈矩阵,具体求解方法更加复杂,建议参考文献[11-12]。
1.2 约束条件
1)火电机组约束
机组出力上下限约束:
un,tpg,n,min≤pg,n,t≤un,tpg,n,max
(5)
式中:pg,n,min和pg,n,max分别为火电机组最小和最大出力。
机组爬坡约束:
pg,n,t-1-RD,n≤pg,n,t≤pg,n,t-1+RU,n
(6)
式中:RU,n和RD,n分别为本区域机组n的上下极限爬坡速率。
最小开停机时间约束:
(7)
式中:Tn,t-1,on和Tn,t-1,off分别为机组n在t-1时段连续开、停机小时数;Tn,on和Tn,off分别为机组n最小开停机时间。
2)风电出力不确定集合的构造
将每个区域中的风电等效为一台出力不确定的发电机组,采用文献[13]提出的概率分布模型表示风能的不确定性,进一步构造风电出力不确定集合,如式(8)所示:
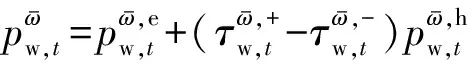
(8)
(9)
(10)

3)系统约束
功率平衡约束:

(11)

负荷需求约束:
(12)

4)联络线功率制定方案
联络线输送容量约束:

(13)
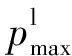
由于风电出力区域之间往往互补,故将日前风功率预测考虑到联络线调度的计划制定中,本文采用文献[14]给出的“传统关口调度结合风电消纳”控制策略,即联络线功率日前调度计划为考虑风电出力区域间协调消纳的联络线功率计划调整值与不考虑风电出力的传统“关口调度”计划值的叠加,如式(14)所示:

(14)

(15)


2 区域间的非零和博弈
2.1 区域间博弈矩阵
将博弈因子视为参与博弈的局中区域行为决定参数,由上文可知博弈因子Ipl和Jpl为带约束的多变量函数,则设Ipl有M个机组启停策略变量,即策略集S1={α1,α2,…,αM},其中α表示T×机组数阶的0-1矩阵;Jpl有N个机组启停策略变量,策略集S2={β1,β2,…,βN}。局中因子Ipl从策略集S1中选一个策略αi,Jpl从策略集S2中选一个策略βj,这样就构成一个局势(αi,βj)。对应于策略集S1和S2,一共有M×N个局势,在局势(αi,βj)下局中博弈因子可记为(Ipl,ij,Jpl,ij),形成用双矩阵形式表示的二人非零和博弈[15]。
理性区域是不会采取对自己不利的严格劣策略的,因此,在分析策略集元素较多的上述类似博弈可能出现的结局时,可以先删除包含严格劣策略的博弈因子。本文采取的筛选方式为插入判断语句,与系统孤立运行下的成本(Is,Js)比较:如果在αi策略中,∀Ipl,ij≥Is,则删除策略αi;如果在βj策略中,∀Jpl,ij≥Js,则删除策略βj。其中:
(16)
删除严格劣策略后,会生成一个新的等效成本博弈矩阵,一共有m×n个局势,如式(17)所示。

(17)
2.2 纳什均衡与混合策略纳什均衡
纳什均衡为由博弈因子形成的一种平衡局势,在纳什均衡点上,任何理性的局中区域都不会有单独改变策略的冲动。在确定的启停局势下博弈因子将为随pl改变的不确定值,有效策略维度也随之改变,因此本文寻找纳什均衡是不断迭代和更新的过程[16-19]。
目标函数:

(18)
找到的纳什均衡策略(α*,β*)满足以下不等式:
(19)

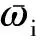
X=[x1x2…xm*]

(20)
Y=[y1y2…yn*]
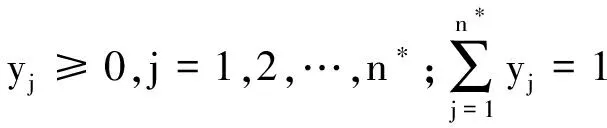
(21)
(22)
进一步本文采用文献[18]提出的非零和博弈策略迭代算法寻找纳什均衡点,具体步骤如下。

步骤2:采用文献[17]提出的离散粒子群算法生成m个pl粒子,求出相应最优策略αj和βj,并求解区域内机组出力得Ij和Jj,得到元素{αj,βj,Ij,Jj},j=1,2,…,m。


步骤5(策略更新):利用循环语句删除重复的Sj,生成新的策略集S,设n=n,i=i+1,跳转到步骤2。
可以证明[20]当i→∞时,以上算法得到的(αk,βk,Ik,Jk)将分别收敛到策略的最优解(I*,J*)和最优纳什平衡策略(α*,β*)。
2.3 谢林点
对于存在多重均衡的博弈,预测究竟哪一个均衡会出现是一个复杂的问题。考虑到互联电力系统的合同行为,本文在最终策略多重均衡上,采用帕累托标准分析确定本次博弈的谢林点。设均衡点数为n,则由式(21)得(X*,Y*)。寻找混合策略对应元素最大值,如式(23)所示,所得(X,Y)即为谢林点(α,β)。

(23)
3 基于离散粒子群算法的求解步骤
本文通过MATLAB软件编程,首先参考文献[13]生成风电出力场景,内部采用离散粒子群算法生成满足约束的联络调度初始粒子群,每个粒子内部机组启停出力策略自行进行非零和博弈找出纳什均衡点,以及各自的期望值,并以此为参考更新个体历史最优以及群体最优。迭代一定次数之后输出趋于收敛的最优群体,并在群体中进行二次非零和博弈,同样采用文献[16]提出的策略迭代法,并直接按照帕累托标准在多重纳什均衡中确定最优解。简化步骤如图1所示。

图1 非零和博弈调度流程Fig.1 Flow chart of scheduling based on non-zero-sum game
需要指出的是,在进行每个粒子下的博弈时,本文启用MATLABPOOL并行计算生成对应粒子群的解,方便进行下一步群体内部的博弈,提高计算效率。
4 算例分析

4.1 非零和博弈联络线调度决策对系统运行成本的影响
为了更好地对比分析结果,本文设计以下场景。


1)场景3与场景1对比分析
场景3下互联系统鲁棒经济调度总成本为1 067 989美元,相比于场景1节约12 841美元,经分析发现场景1和场景3的G5至G10机组状态有差别,如图2所示。

图2 不同场景下的机组组合Fig.2 Unit combinations in different scenarios
从图2可看出:场景3的非零和博弈联络线调度同样可以实现区域之间协调消纳风电出力。由于联络线功率计划的制定将不同区域风电互补特性纳入考虑,使得区域内部对火电机组的旋转备用需求变小,在该调度模式下机组G10保持在停机状态,减少启停成本和固定成本9 934美元。
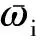
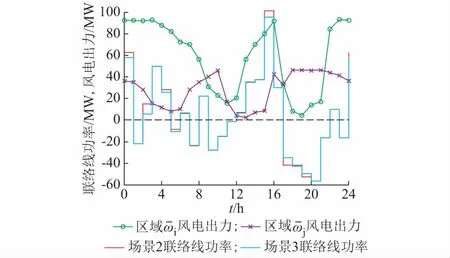
图3 场景3联络线功率及区域风电出力Fig.3 Tie-line power and regional wind power output in scenario 3
2)场景3与场景2对比分析

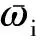
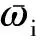
4.2 参数γ和ηt对非零和博弈下各区域等效成本的影响
参数γ和ηt是各个区域风电消纳积极性的直接影响因素,本文采用控制变量法对其进行研究。


表1 γ对互联系统经济调度的影响Table 1 Influence of γ on economic scheduling of interconnected systems


表2 ηt对互联系统经济调度的影响Table 2 Influence of ηt on economic scheduling of interconnected systems
5 结语
通过联络线功率调节来消纳风电,转移系统内部备用容量从而减小总备用剩余,可提高互联电力系统整体的经济效益。为了进一步体现“开放、平等、协作、分享”的互联网精神,本文提出一种基于非零和博弈的互联系统协同消纳风电策略,使各区域能够站在合作的角度进一步强调自身效益最大化,通过博弈环节实现以进一步分配的形式共享能源互联网大背景下系统互联所带来的经济效益,从而提高其在互联系统中参与风电消纳的积极性。通过建立博弈因子,采用离散粒子群算法结合策略迭代法寻找纳什均衡,进一步采用帕累托最优分析法确定最终博弈结果。利用MATLAB软件编程,进一步采用MATLABPOOL并行运算提高计算效率。

本文互联系统中只涉及了两个区域之间的非零和博弈,当存在3个以上的参与者时需要考虑多人非零和博弈,博弈模型更复杂,下一步将对此方面进行研究,以期得到不受参与者数量约束的基于非零和博弈的区域间协调消纳风电模型。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
