强化数学活动 培养模型思想
2018-07-12张美贤
张美贤
(长泰县教师进修学校,福建 长泰 36390 0)
模型思想揭示的是数学对象内在的数学关系结构。数学模型体现着数学的基本方法、基本规律。数学的丰富与发展过程本质上来说就是在不断的抽象、概括和模式化的过程。所以,真正意义上数学教学应该深入到“模型”“建模”的意义上,着力于数学应用和实际问题解决的“模型思想”这一核心。
一、着力画图活动促建模,培养模型思想
在教学实践中,我们让学生经历“弄清题意—明确数量关系—列式计算—检验答题”的过程,这属于解决问题的一般程序模型。在这个过程中让学生从问题入手或从已知条件入手分析题意,找出中间问题,都要让学生通过写一写、画一画来梳理数量关系,把实际问题转化成数学模型。借助画线段图来直观展现、辅助理解。枝形图的画图、分析过程就是在建立模型的过程。
例如,教学关于“归一”数量关系的问题解决:“妈妈买3个碗用了18元,如果买8个同样的碗,需要多少元?”教学的重点是引导学生借助多种直观图的展示来分析数量关系,建立归一问题的数学模型。教学时,在学生阅读审题,弄清题意后,引导学生根据问题条件信息,提炼数量关系,并用不同方式简明显示,通过讨论交流,引出以下四种分析策略模式:

此时,教师抓住时机引导学生对上面各种解题策略模式进行分析、比较、梳理、优化,沟通各种方法之间的联系:作品1用简单的文字把重要的数学信息摘录下来;作品2和作品3用简单的图形(小棒、圆形)清晰地表示数量关系;作品4用单价、数量、总钱数之间的关系求出1个碗的价钱和8个碗的总钱数。于是,教师把数学教材解题例法(作品3)贴到黑板上,引导学生结合直观图列式解答并说出算理:18÷3=6(元)是每个碗的价格,6×8=48(元)就是8个碗的总钱数。当学生明白每一步的算理后,教师又追问:如果我要买20个碗共要多少钱呢?85个呢?100个呢?让学生发现数量变了,总价也变了,但一个碗的价格始终不变。然后出示一道变式题:3个碗是18元,30元可以买多少个同样的碗。有了前面的知识模型基础,学生很快就列出算式,有的用分步计算18÷3=6(元),30÷6=5(个);有的列综合算式30÷(18÷3)=5(个),能运用小括号来计算的同学就已经抓住了问题的关键:先求出单价,再用总钱数除以单价求出数量。当学生建立了有关单价、总价、数量的关系模型后,教师再出示题组让学生进行对比练习:(1)小林读一本书,4天读了24页,按这种速度,5天可以读多少页?(2)买5张同样的书签用了10元,20元可以买几张?(3)同学们大扫除,2名同学擦8块玻璃。教室共有28块玻璃,一共需要多少名同学?……让学生经历从“一个”到“一类”的问题的模型建构,使学生深刻理解了解决归一问题的模型意义,凸显了数学本质,不仅积累了活动经验,而且培养了数学模型思想。
二、注重操作活动促建模,培养模型思想
课堂上,学生探究知识的重难点时,通过动手操作,并引导动口表述、动脑思考,经历知识的形成过程,这一过程就是学生的数学建模过程。学生获得的不仅是知识与技能,更是一种透过现象寻找本质的认识事物的方法。所以,教学应从学生的已有生活经验出发,让学生在操作活动中经历知识形成的三个环节:动作、语义表征相结合理清实际问题—转化为数学问题—进一步抽象化并建立数学模型。
例如,教学“植树问题”时,为了找到植树问题的知识原型,寻找知识生长点,上课一开始,教师先创设情境,引发学生探究兴趣:同学们要在全长800米的小路一边植树,每隔5米种一棵(两端要栽)。一共需要多少棵树苗?首先让学生尝试画线段图方法来体现数量关系,学生在画图过程中“碰钉子”,感到800米画起来有点长,要研究有点麻烦,此时,教师再抛出问题:有没有办法用一个更简单的例子来进行分析推理呢?引出需要从5米、10米、15米……逐步研究起,以“化繁为简”的数学思想出示两道题让学生自主探究,感悟两端都栽的直观模型:(1)全长5米(10米、15米、20米)的小路,平均每5米分一段,可以分几段?(2)在全长5米(10米、15米、20米)的小路一边植树,每间隔5米种一棵,可以种几棵?要求同学用自己喜欢的方法表示出想法:学生有的用小棒摆一摆;有的用线段图画一画;有的列式算一算等方法进行研究。教师巡视时发现有的学生用小棒5米5米的摆,摆到20米的模型是1 1 1 1 1,理解了间隔的含义;有的学生先画出20米的线段再每5米种一棵,直观图的模样是,初步感知全长与间隔数的关系;有的用包含除的数量关系求棵数:20÷5=4(段),4+1=5(棵),初步感知间隔数和棵数之间的关系。教师根据学生汇报的结果把答案填写在表格里(如表格1),然后引导学生观察表格,说说发现了什么?学生在汇报交流中明白了:用除法算出来的商只是段数,而树是种在“点”上的,植树问题是把这个“段”叫做间隔。全长÷间隔长度=段数,求植树的棵数要用段数再加1。教师此时可以引发学生思考:“全长÷间隔长度=段数”其实就是我们以前所学的“包含除法”的模型,也是除法关系式“总量÷每份数=份数”的模型。借用以前的数量关系式帮助学生探究出两端都栽的植树问题,通过动手操作让学生理解了“棵数=间隔数+1”的数量关系式的由来,当学生清楚了点与段之间的模型关系,就能顺利完成课始创设的情境问题:800÷5=160(段),160+1=161(棵),培养了模型应用意识。

表1
有了前面基本植树模型的建构,教师再次抛出问题,引导学生自主探究植树问题的其它两种情况:现实生活中,当遇到公路一端有障碍物,或者两端都有障碍物的现象,那又能植几棵树呢?让学生利用刚才所学知识独立探究。这时学生都能画出直观图进行动作表征和语义表征,并汇报了自己的发现:只栽一端时,5米长的路上每5米栽1棵,只有1段,能栽1棵;10米长的路上有两段正好栽2棵;15米的路上能栽3棵,段数与棵数是对应的,也就是只栽一端时,棵数与段数相等。还能很快理解两端都不栽这种情况是棵数比段数少1。此时还可用列式的方法发现的,5÷5=1(段),两端就不能栽树。10÷5=2(段),2-1=1(棵)。15÷5=3(段),3-1=2(棵)。……以此类推,两端都不栽的时候是棵数比段数少1。当学生对植树问题的三种模型建构完整时,模型的推广运用解决实际问题的环节也是非常重要,教师可通过联系生活中隐含着与植树问题同样的数量关系,例如排队、栽花、剪跳绳、锯木头等问题,将数学模型与现实问题再次进行抽象、对比,有利培养学生模型思想。
三、加强实践活动促建模,发展模型意识
学生通过躬行实践,在思考、探究、求证、交流等数学活动中,把自己怎么想、怎么做,与小组内同伴、班级的同学交流或者操作演示清楚;在实践中获得的体验感受,实现从生活原型到数学模型的转变,从而明白知识的来龙去脉,抓住知识的根,促进知识的掌握和模型意识的培养。
例如,“相遇问题”中如何引导学生根据已有的数量关系和问题背景的特点解决稍复杂的行程问题:两辆汽车从相距455千米的两地同时相向开出,甲车每小时行68千米,乙车每小时行62千米,经过几小时两车相遇?因为学生在四年级已有了速度、时间、路程关系的知识基础,在研究稍复杂的行程问题时就可以以“情境演示—抽取模型—解释与应用”来展开教学,让学生从已有的生活经验出发,经历将实际问题抽象成数学模型,感受数学问题所具有的“模型”力量。首先,让学生在自主探究中结合直观演示,如:指名两位同学上台相向而行等,把行程中的时间、速度、路程的关系说明白,根据所列的算式迁移类推出新的有关行程问题的模型。汇报交流时,学生流露出不同的解题思维:①用列方程的方法,设相遇时间为x小时,则68x+62x=455(如图1)假设甲乙两车同时从两地出发走了x小时相遇(小红旗位置是相遇点),那么甲车走的路程是68x,乙车走的路程是62x,再把两车走的路程加起来就是两地的全路程了。此时教师追问:为什么要把两人走的路程加起来?让学生在汇报交流中明确:因为两车走了x小时相遇,同时出发速度快的路程走得多,它们都没有走完全程,所以两车行驶的路程加起来才是甲乙两车走的全程。学生有的说:②用分步计算,68+62=130(千米),455÷130=3.5(小时),(如图2)第1小时甲车走了68千米,乙车走了62千米,那它们1小时就共走了68+62=130千米,那455千米里面有几个130千米呢?这个几就是两车的相遇时间:综合算式455÷(68+62)。68+62先求出1小时两车走的速度,那总路程除以速度就能求出走的时间。
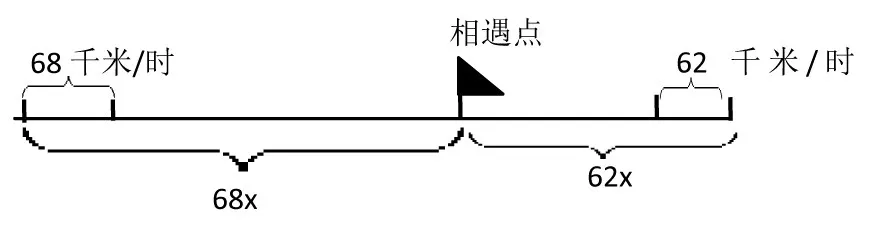
图1
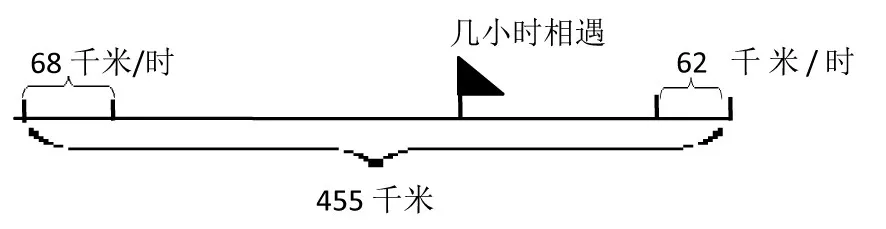
图2
这时教师再追问:这个“速度”跟我们以前的“速度”一样吗?并结合课件演示理解“速度和”,这种开放式建模有利于培养学生的思辨能力,突出数学思考,增强应用意识。
这样的教学因为有了让学生亲身参与课堂活动的机会,充分调动起学习潜能,使得学生对数学建模的价值功能获得更全面、更深刻的理解,学生的数学素养就能获得长足发展。
