空调系统负荷分段预测与研究

施丹 许必熙

南京工业大学电气工程与控制科学学院

0 引言

负荷预测的原理是通过收集历史数据来建立科学有效的预测模型，采用有效的算法进行大量试验，并根据某些准则不断修正模型和算法，得到近似真实的负荷变化规律[1]。基本过程有以下三点：数据采集，数据处理和建立预测模型。负荷预测方法可以分为定量预测和定性预测两大类，暖通空调领域的负荷预测常采用定量预测，其中较为常用的方法有指数平滑法，线形回归法，灰色预测法及神经网络法[2]。指数平滑法的前身是移动平均法，其根据平滑次数的不同可分为一次指数平滑法，二次指数平滑法和三次指数平滑法等。虽然分类各有不同，但指数平滑法的基本思想是预测值是以前观测值的加权和，且对不同的数据给予不同的权，新数据给较大的权，旧数据给较小的权[3]。线性回归法所建立的预测模型是一种解释性模型，它是目前应用最广泛一种预测方法。灰色预测法模型又称为GM(M,N)模型，即M阶N个变量的微分方程的灰色预测模型[4]。当灰色预测方法被应用于暖通空调负荷预测时，如果变量选取为干球温度，那么建模后输出的是下一时刻的干球温度，所以仅建立一个GM(1,1)模型是远远不够的。一般的解决办法是建立多个模型得到温度后，再建立日负荷与温度的关系模型。

神经网络法是利用人工神经网络对非线性系统的良好逼近能力，辨识出空调负荷预测等效模型[5]。本文将详细描述神经网络负荷预测建模的原理。文献[6]对以上四种预测方法的累计误差平均值和相对极差做对比，如表1所示。就累计误差平均值S来说，其所得值越小，则相对的预测精度越高。就相对极差R来说，所得极差百分比越低，则相应的稳定性越好。

表1 预测方法对比

通过综合比较和查阅文献来看[7]，这四种方法各有优势：指数平滑法的建模复杂度低，在负荷预测方面的移植性好，无法联系扰动因素，预测精度较低。线形回归法的建模难度较大，且移植性不佳，预测精度相对较好。灰色预测法在建模前需先处理历史数据，工作量较大，可以得到较精确的参数，预测值的精度也是较高的。神经网络法在学习和训练过程要花费较多时间，稳定性较好，预测精度也最高。因此在本文中，选用神经网络的方法建立负荷预测的模型。

2 预测模型的建立

本文根据空调系统运行的实际情况，设定系统的优化周期为一个小时，即每个小时进行一次负荷预测，预测的是该采样时刻下一个小时内的空调负荷，以此负荷值作为空调系统控制参数优化的依据和约束。利用BP神经网络建立空调负荷预测模型的主要步骤如下[8]：

1）确定预测模型的输入与输出参数

本文选取影响建筑物空调负荷的主要几个因素作为BP神经网络的输入：一是室外的气象参数，包括室外干球温度Tout，绝对湿度Wout、太阳辐射度Ssun；二是室内环境参数，主要是室内温度Tin。输出参数为建筑物下一个小时的空调负荷Qload。

2）确定神经网络预测模型结构

根据上一步，可知神经网络模型的输入参数有4个，输出参数为1个，即神经网络的输入节点有4个，输出层节点为1个。

对于隐层层数的选取，根据Kolmogorov定理，设置一个输入层，一个输出层，一个隐层的三层BP神经网络已经可以满足建模要求。本文采用单隐层的BP神经网络。为确定最佳的隐层节点数，本文采用式（1）所表示的经验公式：

式中：m为隐含层节点数，n为输入层节点数，l为输出层节点数，α通常取1～10之间的常数。

此处n为4，l为1，因此可以得到m取值为4～13。然后利用试凑法得出隐层节点数目为10。因此如图1所示为BP神经网络模型结构。

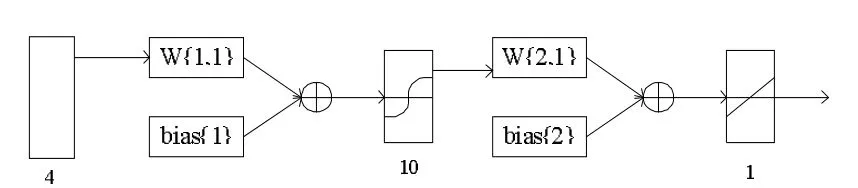
图1 BP神经网络模型结构

本次使用的Sigmoid函数作为隐层神经元激发函数为：

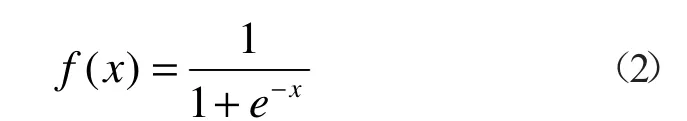
输出层激发函数为线性函数purelin：

3）训练数据归一化

根据文献[9]所述，对神经网络训练之前，需要对所采集的数值进行归一化处理，即采集后的数据数值需要在区间[0，1]以内。计算方法如式（4）：

式中：为输入参数转化后的采样值；xi为输入参数原始采样值；xmin、xmax分别为输入参数采样区间内的最小值和最大值。

隐层激发函数sigmoid的取值范围为(0，1)，函数的临界值0和1无法取到，所以不能充分地逼近目标量的极值。在逆变换时就会引起输出与目标量在极值区产生转换误差，造成输出失真，还影响了其收敛速度。式（4）可以使归一化的值得到压缩，消除了逆变换时的失真，也使函数离开了饱和区，避免了训练过程中产生的局部麻痹现象。

最后利用式（5）把训练后得到预测模型的输出值op转化为实际值：

式中：ypo为输出值转换后得到的实际值；ymin、ymax分别为输出参数原始目标值中的最小值和最大值。

4）神经网络预测模型的训练

本文采用基于梯度下降的BP算法来训练网络，性能函数是均方误差MSE（网络输出和目标输出之间的均方误差），随机初始化权值和阈值，学习速率为0.1，设定准确性校验次数为100。训练时采用批处理方式训练样本，并对权值和阈值进行更新，设定最大训练步数为1000步，训练目标期望误差为0。

本文选取了夏季工况下，博物馆开放时间的682组数据作为神经网络训练的样本，并预留了8月22日到8月28日的77组数据作为测试样本，检验其泛化性和准确性。

5）神经网络预测模型效果的检验

神经网络的训练结果如图2、图3：

图2 负荷预测模型的均方误差曲线

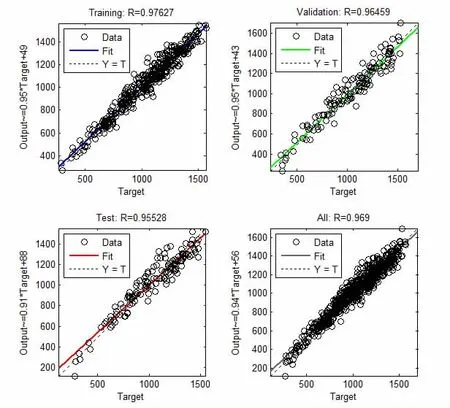
图3 预测模型输出结果的回归分析

从训练的均方误差曲线来看，此次训练的步数为1000步（训练时间为13秒），最小均方误差为0.00675，出现在第123步，训练结束的依据是达到最大训练步数1000步。从训练得到的结果来看，本次建立的神经网络预测模型的有较好的收敛性，均方误差下降很快。

从预测模型输出数据的回归分析图来看，预测模型输出和目标输出的适应度很高，都在0.95以上，基本可以满足负荷预测的要求。从测试样本的回归分析图来看，大部分数据能比较好的切合目标输出，但还是有一些数据点明显偏离了目标输出，可见预测模型还是有一些误差的。

将预留的77组测试样本输入训练好的神经网络，经过检验，结果如图4：

图4 预测负荷与实际负荷的对比

根据图4可看出，预测负荷与实际负荷在整体趋势上相同，基本可以拟合建筑物实际的负荷曲线，但在某些样本处，也出现了比较大的偏离。

从预测负荷与实际负荷的误差图（图5）可以方便的看出，预测的负荷值与实际值的偏差大多在±80 kW以内，个别样本的误差接近100 kW，误差率约为5%左右。总体上来看，神经网络负荷预测模型能基本预测出建筑物空调负荷，虽然误差率不是很大，但在某些点的绝对误差却比较大，影响了负荷预测的效果。

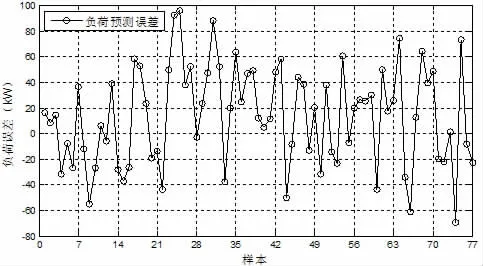
图5 负荷预测误差图

3 负荷预测模型的改进

为了解决预测精度不高和收敛较慢的问题，本文采取了一种基于退火算法的遗传算法融入BP神经网络算法[10]。并且考虑到博物馆工作日和休息日的人流量有很大不同，五个工作日的人流量应该大体相同，两个休息日的人流量也应大体相同，因此采用分段预测的方法，分别建立工作日和休息日的负荷预测模型，两个模型分开训练，从而尽量消除人流量对负荷的干扰。

基于遗传算法的BP神经网络算法思路如下：

1）以BP神经网络为主，将模拟退火算法融入遗传算法中。主要是通过遗传算法的迭代求解最佳初始阀值和权值，避免陷入局部极小值，以达到较好的准确性。在之前的训练样本输入输出数据归一化操作结束以后开始进行，先对新产生的个体进行其邻域内的局部搜索。这种应用使得个体能够向着全局最优的方向进化，能够更好的控制交叉和变异操作，使算法更加稳定，效果更好。

2）初始化群体，随机产生一个群体并对其进行编码，计算其适应度，然后进行精英选择。不同的是，形成一种改进的精英选择法，让精英并不是直接进入下一代，而是以状态接受概率不进入到下一代。有效避免了精英选择法可能造成的早熟现象，而到了进化后期，状态接受概率较小，此时的精英直接进入下一代的可能变大，既加快了局部搜索的速度，又保证了算法的收敛性。

根据以上的思路，可以得到遗传算法的主要流程如下：

1）初始化：

确定种群规模N，交叉概率Pc，变异概率Pm，进化代数G。根据数据情况随机挑选有效个体组成初始化群体P(t)，初始化遗传代数计数器t→0。

设定退火初始温度T0，退火衰减因子k，内循环的迭代计数器len→0，最大迭代次数L(t)，退火的最低温度Tend等有关模拟退火参数。

2）计算当前种群的个体适应度f(xi)，i=1,2,3…N。

3）改进的精英选择操作：

对于精英 xbest，如果 exp((favg-f(xbest))/Tk)＜random(0,1)，则直接进入下一代，否则仍按轮盘赌方式选择。

4）进行交叉、变异操作。

5）进行退火过程：

在变异操作后产生的个体x'i的邻域寻找新个体xi''，计算两者的适应度函数值f(x'i)和f(x''i)。如果满足：min{1,exp((f(xi'')-f(xi'))/Tk)＜random(0,1)}，则用 x''i代替x'i，并判断是否达到内循环终止条件，是则进入（6），否则重新执行（5）。

6）判断进化终止条件：

根据情况做出判断，如果达到进化代数，则转至步骤7，如果没达到进化代数，则进化代数t=t+1，并且更新温度参数T，转至步骤2。

7）判断退火终止条件：

判断结果是否符合条件，如果是，则转步骤8，如果否，则转步骤5单独进行退火操作。

8）计算结束，输出最优结果。

先将原有的训练样本数据分为工作日数据和休息日数据，确定好比较良好的阀值和权值后，然后代入两个BP神经网络分开训练，具体步骤与上一节相同，不再赘述。

将训练完毕的BP神经网络用测试样本分开检验，工作日负荷预测模型训练结果如图6、7所示：

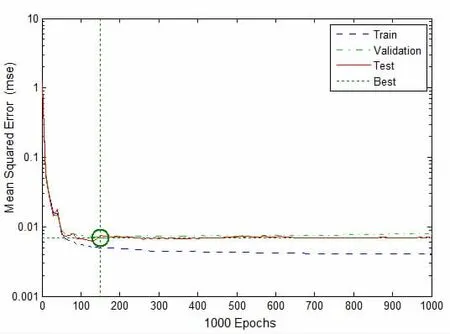
图6 工作日负荷预测模型均方误差曲线

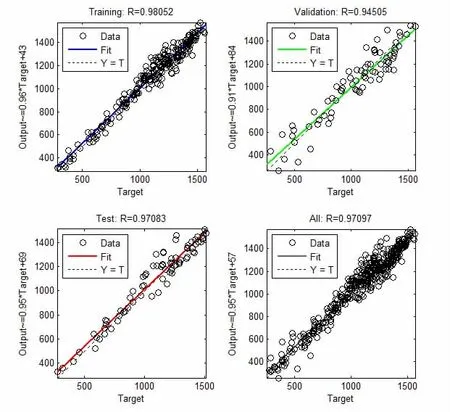
图7 工作日预测模型输出结果的回归分析

由图8工作日可以看出，跟没有改进之前对比，负荷预测模型效果很明显，已经能比较准确地预测出实际负荷值，预测曲线的走势很贴近实际负荷。

图8 工作日预测负荷与实际负荷对比

从误差曲线图9可以明显看出，负荷误差相对于之前预测的误差，已经减少了很多，大多数误差在±40 kW以内，误差率在3%以内，预测精度已经基本满足负荷预测的要求，可以实现对工作日的负荷预测。

休息日负荷预测模型训练结果如图10、11所示：

图9 工作日负荷预测误差

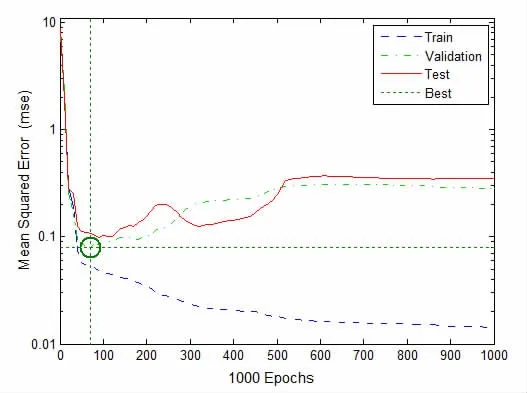
图10 休息日负荷预测模型均方误差曲线

图11 休息日预测模型输出结果的回归分析

从休息日的负荷预测曲线（图12）来看，预测模型的效果相对之前已经有了很大的改善，能较好地拟合实际负荷，但还是有一些误差。

图12 休息日预测负荷与实际负荷对比

从休息日的误差曲线来看，尽管在误差值上，改进后预测的误差要小得多，但大部分的误差都为正数，说明休息日的负荷预测值还是有点偏小。总体而言，根据结果对比，分段后融入遗传算法的BP神经网络预测模型的预测精度得到了明显提升，其具有较好的非线性映射能力，能根据输入的参数预测出建筑物下一个小时的负荷，预测的空调负荷较实际值的跟随性也比较好，能够满足负荷预测的要求。

图13 休息日负荷预测误差

4 结束语

本文首先简要介绍了空调常见的基本负荷预测的方法，然后基于BP神经网络算法对博物馆的负荷建立了预测模型，通过对负荷预测的仿真和验证，结果表明预测模型基本可以预测下一个小时的建筑物空调负荷，但仍有一定的误差。分析产生误差的原因后，融入遗传算法采用分段训练的方法，避免陷入局部极小值，然后分段建立神经网络预测模型，再次检验预测效果，发现预测效果有了明显的提高，误差率降为3%左右，满足建筑物空调负荷预测模型的要求。

[1] 郑慧凡,阎秀英,范晓伟.建筑物空调负荷计算方法研究进展[J].中原工学院学报,2007,18(5):1-5.

[2] 温权,李敬如,赵静.空调负荷计算方法及应用[J].电力需求侧管理,2005,7(4):16-18.

[3] 赵君有.基于灰色理论的中长期电力负荷的预测[D].沈阳:沈阳工业大学,2007.

[4] 陈娟,吉培荣,卢丰.指数平滑法及其在负荷预测中的应用[J].三峡大学学报(自然科学版),2010,32(3):37-41.

[5] Wang H, ChangWL. Load forecasting for electrical power system based on BP neural network[C]//International Workshop on Education Technology and Computer Science.IEEE,2009:702-705.

[6] 赵波峰,文远高,杨恒.四种空调负荷预测方法分析比较[J].建筑热能通风空调,2012,30(6):65-67.

[7] 康重庆,周安石,王鹏.短期负荷预测中实时气象因素的影响分析及其处理策略[J].电网技术,2006,30(7):5-10.

[8] 郑慧凡,白静,李安桂.BP神经网络在建筑物空调负荷预测中的应用评述[J].计算机应用与软件,2007,24(6):103-105.

[9] 柳小桐.BP神经网络输入层数据归一化研究[J].机械工程与自动化,2010,(3):122-123.

[10]程玉桂,黎明,林明玉.基于遗传算法和BP神经网络的城区中长期电力负荷预测与分析[J].计算机应用,2010,30(1):224-226.