LSTM的单变量短期家庭电力需求预测
2018-07-12王旭东陆慧娟叶敏超
王旭东,严 珂,陆慧娟,叶敏超
(中国计量大学 信息工程学院,浙江 杭州 310018)
随着世界人口数目的不断增多,人类对能源需求日趋增大.目前,家庭住宅的能源消耗约占全世界能源使用总量的30%~40%[1-3],住宅负荷经常对季节和日用电高峰需求有显著影响[4].通常,为了满足高峰时期的用电需求,电力公司会提高发电能力以满足需求.但是提升20%的发电能力大约可以应对潜在发生的5%的峰值需求[5],这对电力资源是一种极大的浪费.准确的预测家庭住宅用电需求,平衡用电高峰的供需关系,将会减少电力资源的浪费,对保护生态环境产生积极影响.随着智能电网的出现和大量智能电表的安装[6],降低了数据获取的难度,因此短时家庭电力负荷预测具有可行性和现实意义.
关于家庭层面的用电需求预测,近几年相关研究很多,大部分都采用了机器学习的方法.Ghofrani等[7]使用卡尔曼滤波研究了负荷预测.Humeau等[8]利用支持向量回归和神经网络研究了个体级别的住宅负荷预测和总体水平.Sevlian和Rajagopal[9]研究了预测精度与聚合水平之间的比例关系.Arora和Taylor[10]考虑了负荷预测的条件核密度估计,并讨论了其在分时定价中的应用.Haben等人[11]提出了一种新的评估个体家庭负荷预测误差的方法,以更好地描述波动性和噪声负荷信号.Yu等[12]提出了利用稀疏编码的方式对短期家庭需求进行预测,提升了预测精度.Shi等[13]使用一种基于池化处理的深度循环神经网络来克服家庭电力需求数据随机性大的问题.
近年来,随着深度学习技术的不断发展,一些深度学习模型逐渐被应用到时序数据的研究中[14].其中,循环神经网络(recurrent neural networks, RNN)是一种带有自循环结构的神经网络,允许时间序列数据在网络层上信息流动的持久化,在理论上十分适合处理时间序列数据.RNN产生了众多变体,如双向循环神经网络[15]、长短期记忆循环神经网络(LSTM)[16]、门控循环神经网络(GRU)[17]等.在众多RNN的变体中,LSTM网络弥补了RNN的梯度消失和梯度爆炸、长期记忆能力不足等问题,使得循环神经网络能够真正有效地利用长距离的时序信息.并且LSTM网络已经在股票预测[18]、故障时间序列预测[19]、语音识别[20]、航空发动机过度振动预测[21]等时间序列相关研究领域取得了应用.
本文针对短时家庭电力需求数据维度单一、数据随机性强的问题,提出了一种基于LSTM的单变量短时家庭电力需求预测模型,来对1 h为单位的家庭电力需求进行预测.
1 LSTM循环神经网络
循环神经网络(Recurrent Neural Networks,RNN)是一种具有反馈结构的神经网络,其输入不仅和当前输入和网络的权值有关,而且也和之前的网络输入有关,因此,在理论上说,RNN非常适合处理序列数据.但是用循环神经网络学习长期依赖问题时,会出现梯度消失或者梯度爆炸问题[22],导致模型无法训练.为了克服这一问题,Hochreiter等人[16]提出了长短期记忆循环神经网络(long short-term memory,LSTM),引入了细胞状态和三个门结构控制信息在细胞状态上的更新,实现了信息在网络上的长期流动.
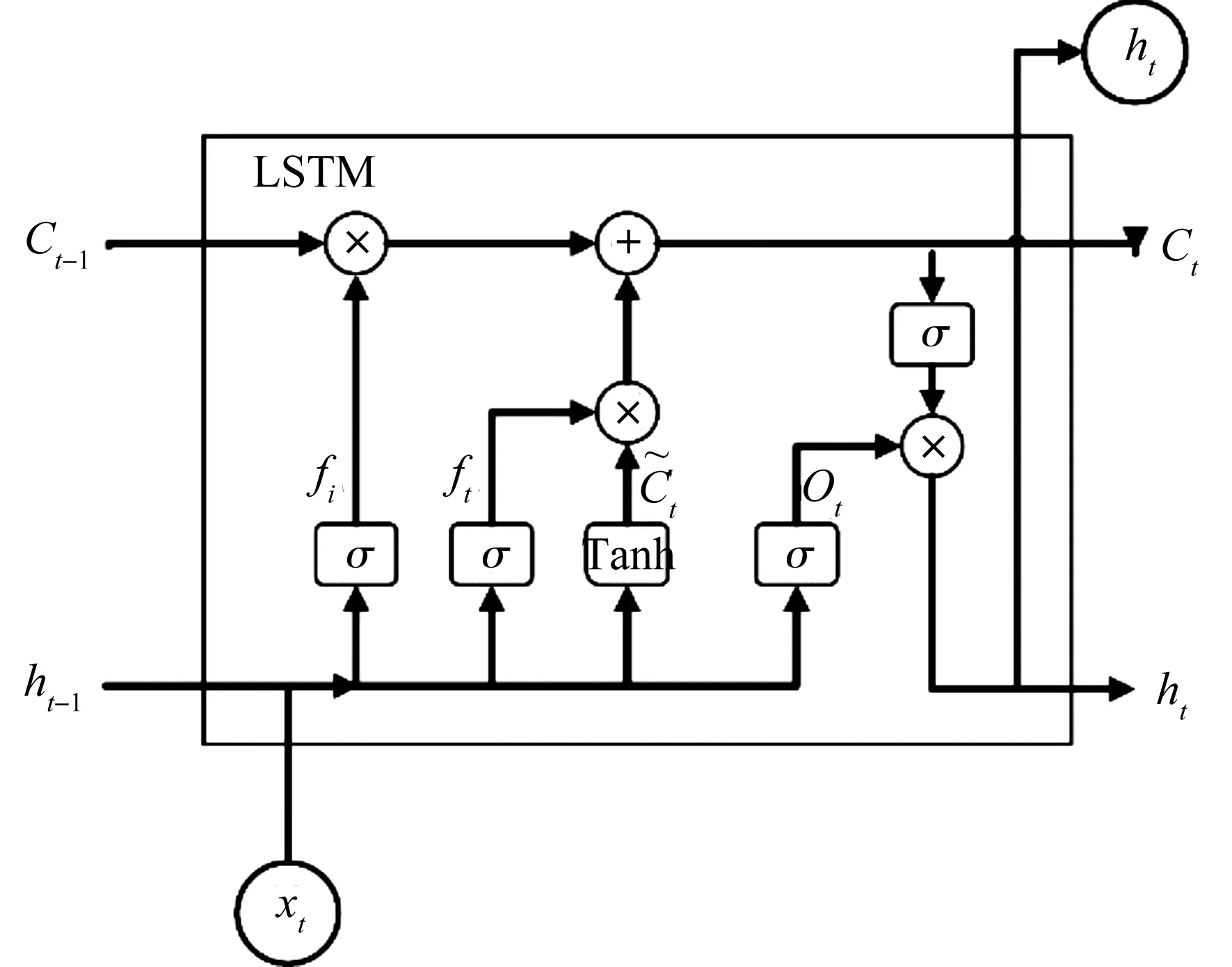
图1 LSTM神经元内部结构图Figure 1 Internal structure of LSTM neural networks
LSTM神经元内部结构如图1.为了建立时间连接,LSTM在整个循环周期内定义和维护一个内部记忆单元状态——细胞状态Ct,然后通过遗忘门ft、输入门it、输出门ot三个门结构来更新、维护或删除细胞状态内的信息.前向计算过程如下:
ft=σ(Wf·[ht-1,xt]+bf),
(1)
it=σ(Wi·[ht-1,xt]+bi),
(2)
(3)
(4)
ot=σ(Wo·[ht-1,xt]+bo),
(5)
ht=ot·tanh(Ct).
(6)

LSTM网络训练过程采用通过时间反向传播算法(back-propagation through time,BPTT),反向计算每个LSTM神经元输出值与真实值的误差项,根据相应的误差项,计算每个权重的梯度,应用梯度优化算法更新权重.
2 基于LSTM的电力预测模型
家庭级别的电力需求数据,是通过智能电表自动采集单位时间内的用电量来收集,相对于城市级别的电力需求数据,家庭电力需求数据维度单一且随机性强,预测难度更大.考虑到家庭电力需求数据的特点,现提出一种基于LSTM的单变量的家庭电力需求预测模型.模型包括输入层、隐藏层、输出层、网络训练及优化四个模块,网络模型整体框架图如图2:
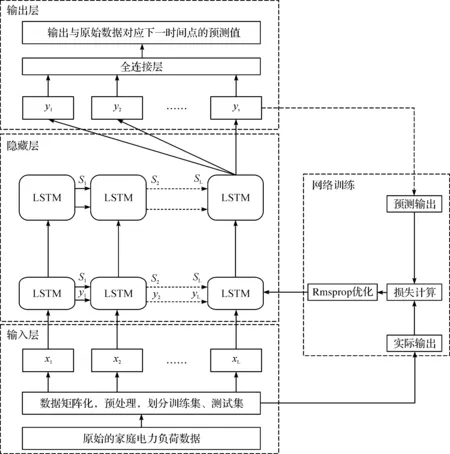
图2 基于LSTM的单变量短期家庭电力需求预测模型框架Figure 2 Short-term forecast framework of household electricity demand based LSTM single variable
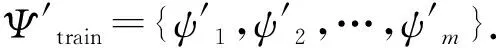
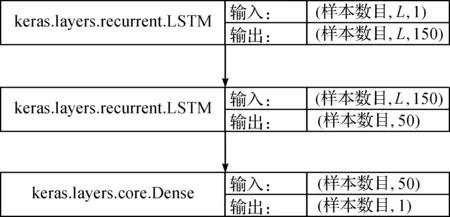
图3 网络层上数据流动形式Figure 3 Data flow-chart on the network layer
由于训练样本基数大,训练过程中优化算法使用小批量梯度下降算法(Mini-batch gradient descent),相对于批量梯度下降,小批量梯度下降每次选取一个批大小的样本更新参数,节省了运算成本,提高了运算速度;相比于随机梯度下降,小批量梯度下降降低了收敛的波动性,使得参数更新更加稳定.网络的损失函数定义为
(7)
其中:B表示一个批次中样本的数量.
学习率η的选取对模型性能有重要影响,同时也常常是模型中最难调试的一个参数,为了降低参数调试难度,使模型表现最优,本文使用超参数优化算法来对学习率η进行参数优化.常用的自适应学习率优化算法有AdaGrad、RMSProp,Adam等,其中RMSprop使用指数衰减平均以丢弃遥远过去的历史,使其能够在找到凸碗状结构后快速收敛,因此选用RMSProp算法作为模型的超参数优化算法.
3 实 验
本章使用英国能源中心提供的英国伦敦家庭电力需求数据,来对提出的基于LSTM的单变量短期家庭电力需求预测模型进行训练及性能测试.
3.1 实验数据
本数据来自于英国伦敦的家庭电力使用记录[23].该数据集使用智能电表收集了五个英国家庭2012年至2014年以6 s为采样间隔的电力消费数据.
原始电力需求数据是以6 s为采集频率采集的,本文是对1 h家庭电力需求进行预测,因此要先进行数据合并得到实验数据集,合并后的数据选取90%作为训练集,其中的5%作为验证集;10%作为测试集,数据具体值如表1.

表1 实验数据集描述
3.2 硬件及软件平台
实验中所用的计算机配置环境为:处理器为Intel(R)Core(TM)i7-7700 CPU @ 2.80 GHZ,内存为8.00GB,GPU为基于Pascal架构NVIDIA GeForce GTX1050显卡,显存为2.00GB;操作系统为Windows10(64-bit);程序设计语言为Python 3.5.2(64-bit);集成开发环境为PYCharm Comm Edition 2016.3.2.深度学习代码后端基于Google的深度学习开源框架Tensorflow训练,版本为tensorflow-gpu 1.30,前端为Keras 2.0.8.
3.3 评价指标
本文选用均方误差(Mean Square Error,MSE)作为评价标准,MSE的计算公式为
(8)
MSE越小,表明预测的用电需求值和实际需求值越接近,预测越准确.
3.4 实验结果及评估
模型使用英国伦敦家庭电力需求数据进行性能评估.其中,迭代次数、学习率是重要的超参数,这些超参数的取值对模型的性能表现产生重大影响,需要选取合适的参数.
当固定学习率为0.005,序列长度为23,批样本为512,优化器选择RMSprop时,观察不同的迭代次数下训练误差和验证误差变化,如图4.
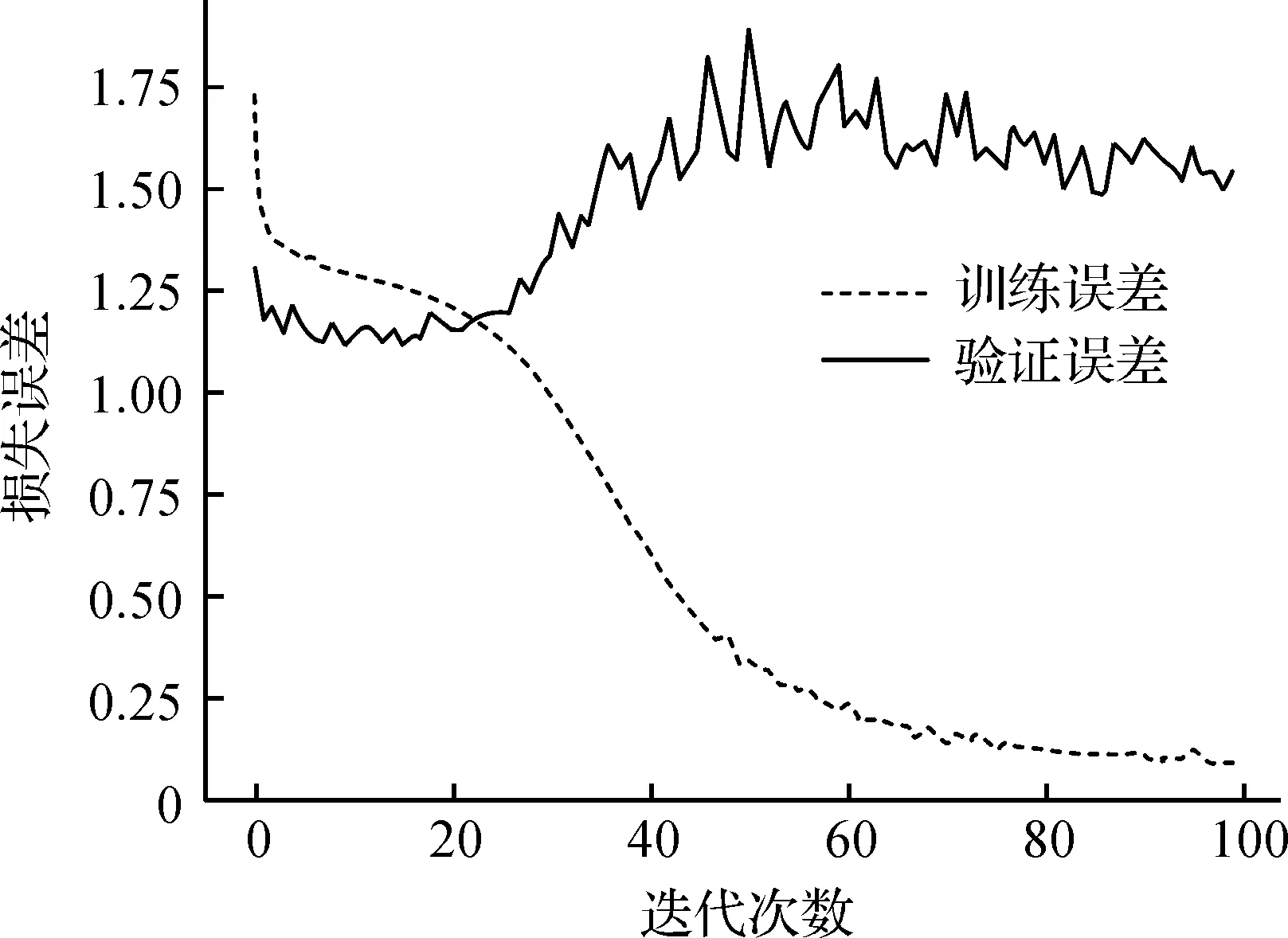
图4 不同迭代次数下,LSTM模型训练误差和验证误差变化Figure 4 LSTM model training error and verification error under different epochs
由图4可以看出,随着迭代次数的不断增大,训练误差呈下降趋势,并且在迭代次数为60之后,趋于平稳;验证误差随着迭代次数增大经历了先下降又递增的过程,这说明迭代次数过大将导致模型产生了严重的过拟合.因此,将迭代次数定为20.
在相同参数下取不同学习率(LR=0.001,0.002,0.003,0.004,0.005)对模型进行训练,得到的预测精度如图5,可清楚的看出,学习率为0.002时预测精度最高(MSE最低),因此,将模型学习率定为0.002.
实验选取不同的序列长度(L=4,6,8,10,12,14,16,18,20,22,24,26,28,30)来训练LSTM模型,预测精度随序列长度变化如图6.序列长度为24时MSE最小,因此,模型的序列长度定为24.

图5 不同学习率下,均方误差(MSE)变化Figure 5 Mean square errors(MSE) in different learn rate
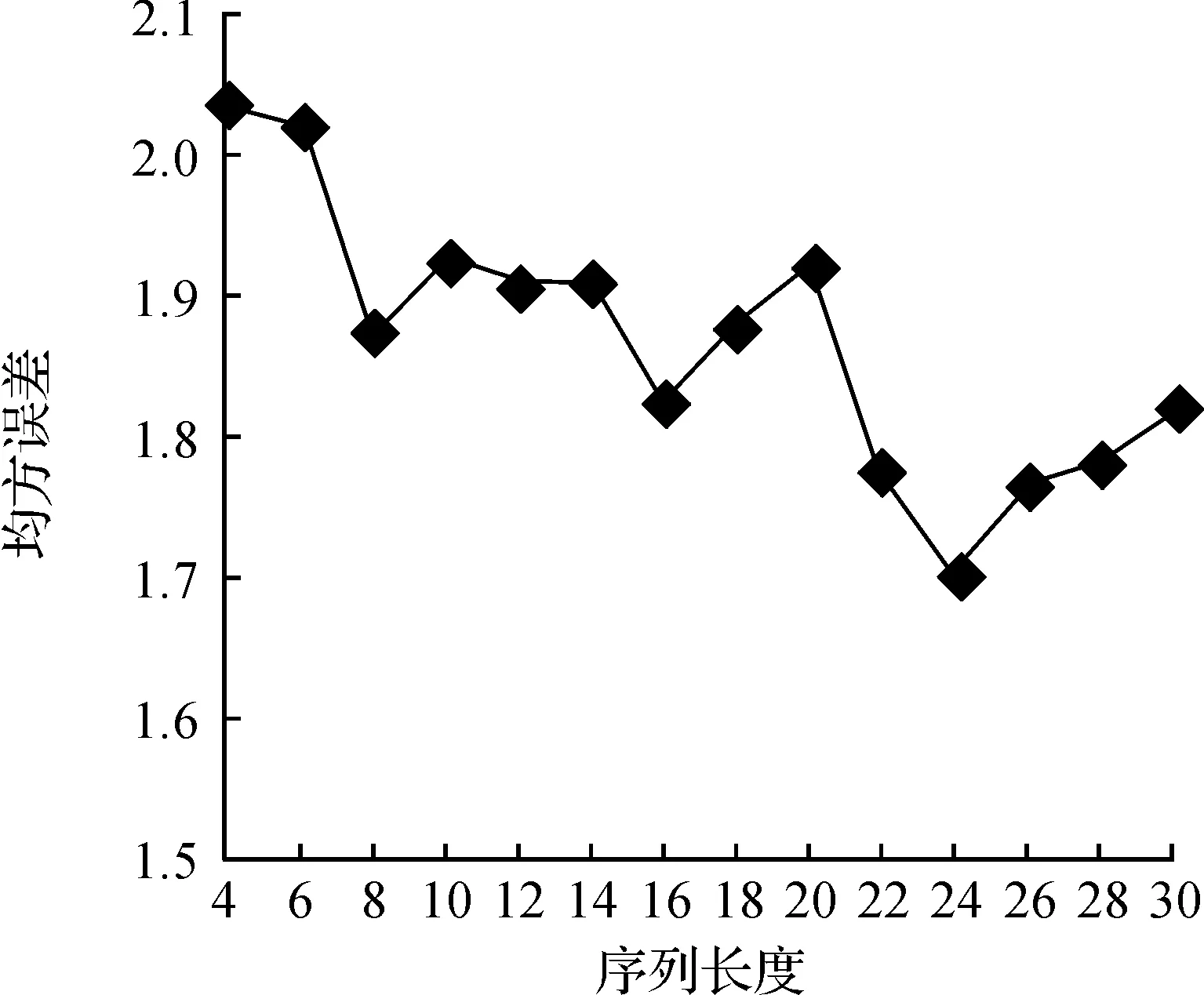
图6 不同序列长度下,均方误差(MSE)变化Figure 6 Mean square errors(MSE) in different sequence length
将本模型在五个数据量、生活习惯不同的用电家庭数据集上进行测试,评价指标使用均方误差(MSE),并和传统的循环神经网络(RNN)、门控循环神经网络(GRU)进行了对比实验,实验结果如表2.从表2可以清楚的看出,LSTM模型在第1、2、5家庭中预测表现最优,而RNN方法只在家庭4中表现最优,GRU方法只在家庭3中表现最优.这说明LSTM短期电力需求预测模型泛化能力比RNN、GRU好.同时和表1联合观察可知,家庭3训练集数据过少(小于1 000),预测精度不高(MSE最高),其余四个家庭数据集MSE在5以下,说明LSTM在训练集大于1 000时表现较好,但是数据集过大(家庭1),精度提升不会过于明显,因此,我们选取家庭2作为实验结果比较的主要对象.
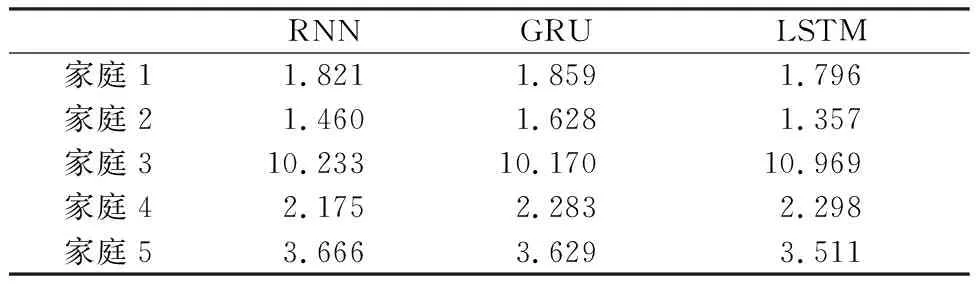
表2 三种方法在5个英国家庭中的均方误差Table 2 Forecasting MSE of three models in 5 British households
图7是LSTM、RNN、GRU三种模型对英国家庭2电力需求预测一周的曲线变化.从图上可以清楚的看出,传统的RNN方法对用电平稳的时间段预测效果较为精准,但是当用电峰值来临时,RNN方法预测误差很大,达不到实际应用要求.LSTM和GRU方法都能够准确的反映家庭2的用电趋势变化,但是本文提出的LSTM模型对峰值拟合程度更高,整体表现更好.同时从表2可知,RNN、GRU、LSTM三种方法在英国家庭2测试集上的均方误差分别为1.460、1.628、1.357,本文的LSTM模型均方误差最小.综上,LSTM模型在整体预测精度和峰值预测表现均优于RNN和GRU方法.当突发性的用电峰值来临时,如115 h、139 h,本文提出的LSTM模型对于突发性的用电峰值预测还存在较大误差.造成这一问题的原因是家庭的用电需求会受到突发性的社会活动影响,这就造成了一个家庭短时间内用电需求的大幅提升,从而影响了预测精度.

图7 三种模型对英国家庭2电力需求预测曲线Figure 7 Electricity demand forecasting results using three models for family 2.
4 结 语
本文提出了基于LSTM的单变量短期家庭电力负荷预测模型,包括模型的框架,网络结构、超参数优化等内容.并使用伦敦家庭用电数据进行训练,对1 h内家庭电力需求进行预测.本模型克服了数据本身特征维度低、随机性强的问题,为智能电网在家庭层面用电需求的准确及时预测提供了保障,对推动个性化用电套餐的广泛普及及减少能源浪费发挥了重要影响.但是,该模型在对用电峰值的预测上精度还不够高,后续的工作准备通过拓展网络层数与寻求更有效的参数优化方法等提高预测模型的峰值预测精度.
