同轴射流流场及冲击传热特性的数值模拟
2018-07-12徐志超周静伟耿丽萍
徐志超,周静伟,耿丽萍
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
同轴射流是指从两根同心的套管中流出的、中心为圆柱形射流、周围则为环形射流混合而成的射流(如图1所示).同轴射流在工业燃烧器、冷却系统、化学反应器等领域均有广泛应用,尤其在燃烧领域,它作为燃烧空气动力学的一个典型问题,得到了广泛重视[1-3].

图1 同轴射流模型示意图Figure 1 Schematic diagram of a co-axial jet
同轴射流离开喷嘴后,中心射流与环流之间发生混合和交互作用,由于存在内外两个剪切层,即两股射流之间的剪切层及外围射流与周边流体之间的剪切层,故近场结构非常复杂.影响同轴射流的因素,除了雷诺数、湍流强度、出口倾角等常规因素影响之外,还涉及到中心射流与环形射流的流通面积之比、速度之比,它们决定了射流的中心区以及混合区长度,因此同轴射流是一种非常复杂的流动现象.
由于同轴射流的空气动力特性对学术研究和实际应用均有重要意义,故对其流动和混合特性的理论与实验研究已有很多[4-7].众所周知,射流的主要应用之一是用于强化冲击换热,即将射流喷射到被冷却表面上以获得高效的冷却效果.由于流体直接冲击被冷却的壁面,能够在壁面上形成很薄的边界层,从而使直接受到冲击的区域产生很强的传热传质效果,是一种极其有效的强化传热方法,在工程上有广泛的应用,如纸张的干燥、金属的回火、钢铁的冷却、飞机机翼除冰、航空发动机涡轮叶片的冷却以及微电子元件的冷却等等,一直受到工业界和学术界的高度重视[8-9].
同轴射流虽然在很多领域受到广泛关注,但是它的冲击传热特性至今尚未引起足够重视,文献中只有很少的一些相关研究的报道[10-12].如今常有各种新颖的射流用于冲击传热研究,如旋进射流[13]等等.同轴射流流动颇有其特殊性,由于存在两股射流的混合作用,会影响势核区及湍流强度,因而它对冲击传热的强化是有潜在可能的,有待深入研究.鉴于传热与流动是密不可分的,本文拟先对同轴自由射流出口的速度场进行模拟,然后对同轴射流的冲击传热特性进行初步的探索,以期对同轴射流的形成和发展及其冲击传热性能有初步的认识,研究重点放在同轴喷嘴结构参数和雷诺数的影响上.
1 数值模拟模型的建立
1.1 物理模型及边界条件
同轴射流物理模型如下:喷嘴由两根同轴空心圆管构成,其中内套管内径d,外径do;外圆管内径D,外径Do,直径比定义为两根圆管的内径之比d/D,内套管长度为L.外圆管为足够长,流体进入圆管后经过充分发展,在内套管的入口处分裂为两部分,一部分进入内套管并在出口处形成中心射流,另一部分进入两管之间的环形通道并在出口处形成环形射流.模型中外圆管的内、外直径D和Do固定为15 mm和20 mm,改变内套管的长度和内外径尺寸,组成如表1所示的四种算例.
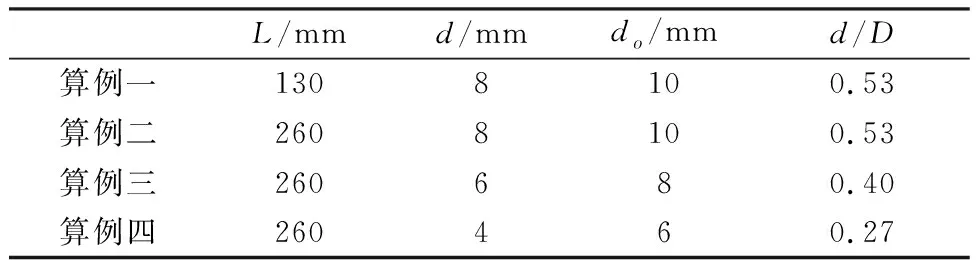
表1 各算例的结构参数
同轴射流喷嘴的结构参数、流动求解区域模型以及坐标系统如图2.数值模拟中将流体看作不可压缩的理想气流,各项流体的参数视作常数,不随温度、速度等变化.研究同轴射流的流场分布和演变特性时,物理模型中不设置冲击换热板,即射流为自由射流.由于射流冲击高度是影响同轴射流冲击传热效果的一个重要因素,在同轴射流冲击换热模拟中,平板距喷嘴出口的冲击高度要作变化,解域也相应发生改变.
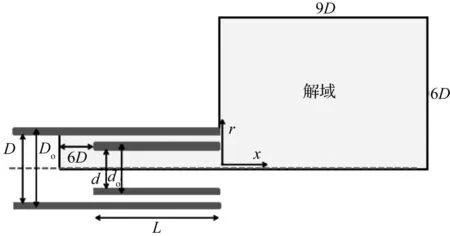
图2 几何结构与解域的示意图Figure 2 Geometric structure and solution domain
模拟采用软件ICEM CFD 15.0完成几何模型并生成网格,如图3给出了出口附近局部的网格图.将模型简化为带对称轴的二维模型,由于研究工作中不考虑冲击平板的厚度的影响,模型中换热板简化为线段.网格采用结构网格画法,靠近管壁附近因为流速变化剧烈,需要加密网格,而轴向方向上则在管道入口和喷嘴出口出口处加密网格.

图3 喷嘴出口附近局部网格结构图Figure 3 Mesh structure near the exit of jet nozzle
数值模拟使用商业软件Fluent 16.0进行,对连续性方程、动量方程和能量方程离散迭代求解.为比较不同工作条件下的流动及换热效果,本文将同轴射流的雷诺数Re、对流传热系数h、努塞尔数Nu分别定义为:
Re=ρ·Uo·D/η,
(1)
h=q/(Tw-Tf),
(2)
Nu=h·D/λ.
(3)
其中:ρ、η、λ分别为流体的密度、动力黏度和导热系数,Uo为喷嘴入口的流速,Tw、Tf分别为壁温和流体温度.
数值计算时的边界条件设置如下:在求解域的入口处设为均匀速度入口,入口速度由雷诺数换算得到;同轴喷嘴内外圆管的壁面均设为无渗透、无滑移的边界条件;喷嘴中心轴线处为对称边界条件,射流流出区域采用压力出口边界条件.射流流动的湍流模型采用RNGk-ε模型.射流流体温度Tf设为293 K,周围流体温度与射流相同,喷嘴本身绝热,冲击换热板为固定壁面,无渗透,无滑移,热流密度取300 W/m2.数值计算采用基于原始变量的有限差分方法,用SIMPLE方法处理压力与速度的耦合,径向和轴向速度方程、切向速度、k和ε方程均采用一阶上风差分格式.计算收敛的标准为各项残差均小于10-6.
图4示例性地给出了一个工况下模拟获得的喷嘴出口附近的流场速度轮廓图.
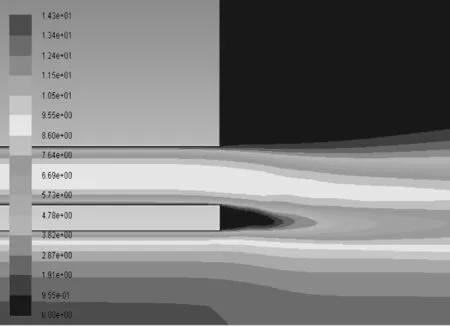
图4 流场流速轮廓图示例Figure 4 Distribution of velocity contour
1.2 网格无关性验证
数值模拟模型的网格数分别选取了50 000,80 000,160 000和210 000,结果表明,当网格数大于160 000时,流场流速分布及换热板温度数据与网格数基本无关,继续增加网格数,努塞尔数之间的偏差将不超过2.6%.因此本文的模拟工作是在此网格模型的基础上进行的.
2 流场模拟结果及分析
2.1 圆柱射流的速度分布
为了便于与同轴射流进行比较,首先给出普通圆柱射流的流场分布.湍流圆柱射流离开喷嘴时,速度呈钟罩状分布,射流沿轴向流动过程中,周边流体被不断卷吸进来,射流会不断扩散开来,射流中心速度逐渐降低.若流速和径向距离均采用无量纲参数,则在不同流量(即不同Re数)下,速度场分布并没有显著的不同,图5给出了Re=14 000时不同位置处沿径向的速度分布.图中纵、横坐标均取无量纲量,横坐标r/D为偏离喷嘴对称轴的径向相对距离,纵坐标u/Uo为射流速度u与来流入口速度Uo之比值.
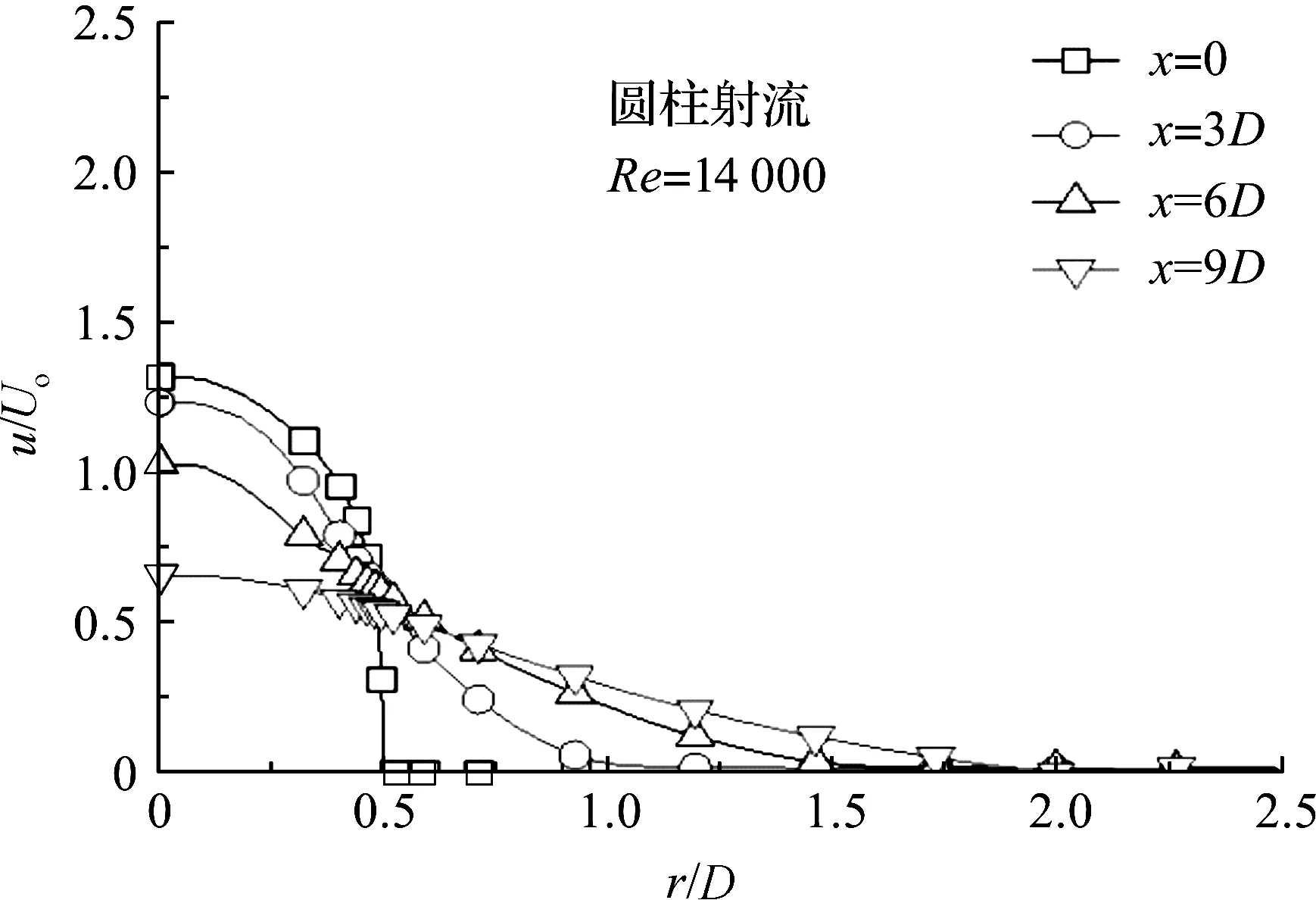
图5 普通圆柱射流流速分布图Figure 5 Velocity profile for conventional circular jet
2.2 同轴射流速度分布
着重研究不同直径比和不同内套管长度的同轴射流离开喷嘴后速度场的分布和演变.取三个不同的雷诺数(Re=7 000,14 000,28 000),对表1中的几种不同喷嘴进行流动模拟,在距离喷嘴出口不同的轴向位置(分别取x/D=0、3、6、9,x/D=0为出口位置)分别给出速度沿径向的分布.图6至图9为各种算例的速度分布图.射流沿径向速度下降很快,当径向距离r/D=2.5后,所有算例的流速已基本趋于零,故横坐标最大值取到2.5为止.
图6为同轴喷嘴算例一(d/D=0.53、内套管长度L=130 mm)的流场分布.由于内套管管壁的存在(厚度为1 mm),出口处(x/D=0)的速度沿径向分布曲线中有一间断,因此形成了双峰曲线.由图4的速度流场可知,在出口附近径向速度分布曲线都会呈现双峰的特点,但双峰持续的长短与直径比有很大关系.
比较图6(a)~(c)可发现,尽管在数值上略有变化,不同雷诺数下的速度分布趋势基本一致.从图中可以看出,在喷嘴出口处(x/D=0)圆柱主射流的中心流速约为入口流速的2倍,明显高于环形通道中射流的流速.随着轴向距离的增加,由于周围流体不断被卷吸进来,射流不断扩散,径向速度分布也越趋平坦.
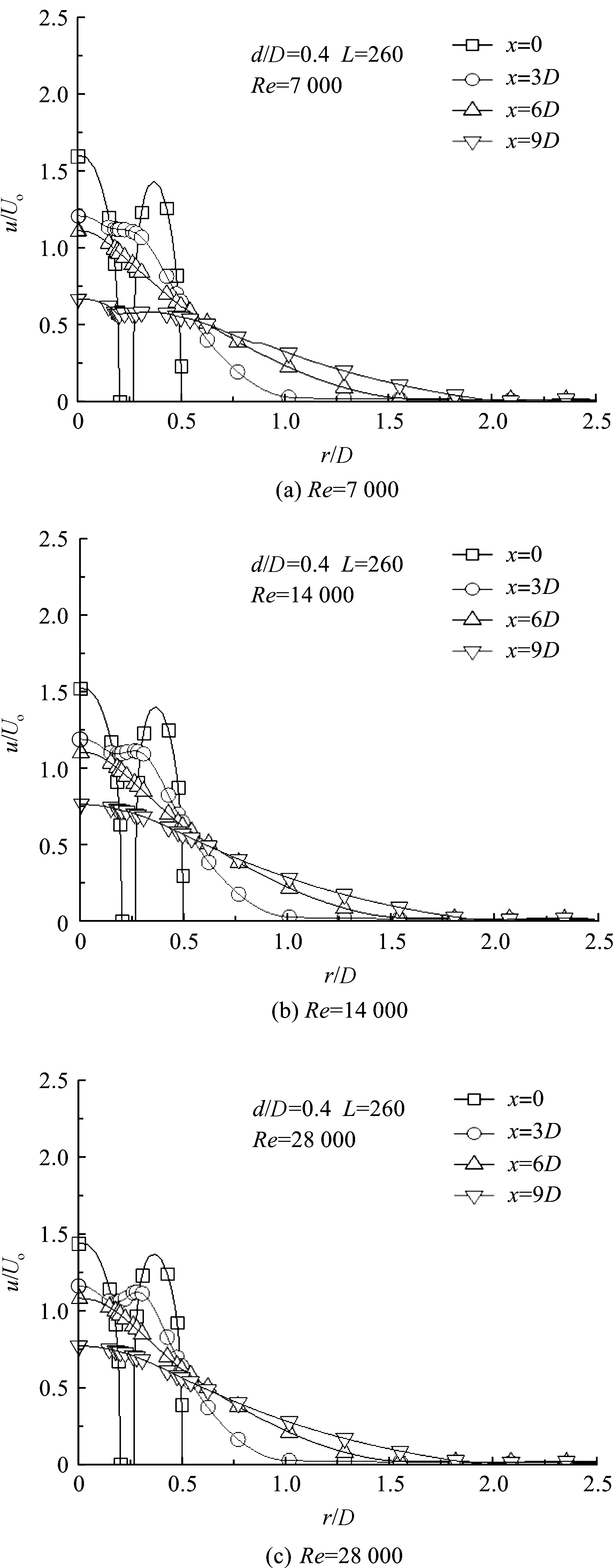
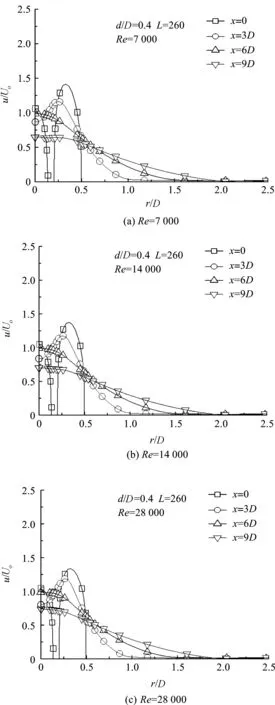
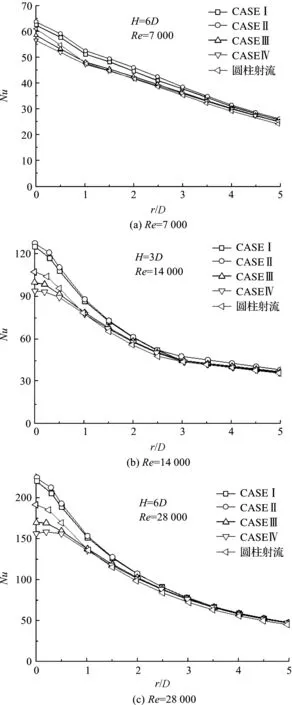
图6与图7中同轴喷嘴的直径比相同(d/D=0.53),区别在于内套管的长度L不同,算例一和二中的L分别为130 mm和260 mm.对比图6和图7可知,L增加时,出口处及出口附近(0 图6 算例一的流速沿径向分布图Figure 6 Radial velocity distributions of CASE I 图7 算例二的流速沿径向分布图Figure 7 Radial velocity distributions of CASE II 图8是对应于直径比d/D=0.40喷嘴的速度分布.此时由于d/D下降,中心圆柱射流的横截面积相应减小.对比各雷诺数下图7和图8的速度分布可见,此时喷嘴出口处的中心速度明显下降,其值约为入口流速Uo的1.5倍,与环形射流中心的流速已相差无几.此时的另外一个特征是,由于内管管壁引起的出口速度分布不连续而呈现的双峰分布现象,在下游x/D=3处仍明显可见其存在,且雷诺数越大越明显.但当x/D>6时,它与算例二的速度分布趋势基本一致,但速度值要小一点. 图8 算例三的流速沿径向分布图Figure 8 Radial velocity distributions of CASE III 图9 算例四的流速沿径向分布图Figure 9 Radial velocity distributions of CASE IV 图9为直径比更小时(d/D=0.27)的同轴射流速度分布.此时同轴喷嘴出口处中心射流的速度与流体的入口速度已不相上下,且明显小于环形射流中的速度.因此出口处的双峰曲线形状与前面的几种情况有所不同. 在下游x/D=3处双峰非常明显,双峰存在的区域更长,持续到3D到6D之间.从图9中还可看出:在x/D=6时的射流中心速度比x/D=3时还要高,这是由于此时环形射流的速度高于中心圆柱射流,射流离开喷嘴后的混合过程中形成对中心射流的加速,这些特点将会影响冲击传热特性. 仔细分析图6~9可以发现,尽管直径比对出口附近速度分布影响很大,但随着离开喷嘴距离的增加,无量纲的速度分布形状越来越趋于一致,x/D=9处各种喷嘴结构参数和流动参数(Re)下的速度分布形状已经基本趋同. 同轴射流由于中心和环形两股射流的混合交互作用,在冲击平板时其换热特性会呈现出某些特殊性.在数值模拟模型中,同轴射流垂直冲击一块恒热流加热的实验平板,通过数值模拟得到平板上温度的分布,进而得到努塞尔数Nu在冲击平板上的分布. 雷诺数仍然取7 000、14 000、28 000三种,无量纲高度H/D取3和6进行分析. 图10为H/D=3时四种同轴射流在三个Re数下的换热效果的数值模拟结果,同时给出的还有普通圆柱射流的模拟结果.算例一和二中的同轴射流具有相同的直径比,只是内套管长度不同,从图6、图7中可见两者速度场的分布基本一致,在冲击传热特性上看两者也基本相同,但在靠近中心附近内套管长度较长的同轴射流传热性能略占优势. 图10 H/D=3时努塞尔数分布图Figure 10 Distribution of Nusselt number at H/D=3 此时冲击高度较小(H/D=3),如果同轴喷嘴的直径比d/D较大,则Nu数随着径向距离增大而单调下降.从图10可见,当直径比d/D减小到0.4时,Nu数随径向先是有所下降,然后回升直至一个峰值,然后再逐渐回落,这一趋势随着Re数的增加更加明显.这与速度场分布有关,当d/D=0.4时,由于内套管壁的存在,中心射流与圆环射流相互作用,x/D=3时沿径向的速度分布双峰尚存(见图8),于是在冲击传热时也呈现出这样的特征,且Re数越大越明显.当直径比更小时(d/D=0.27),同轴射流中环形射流的速度已经远高于中心射流的速度,此时从中心开始Nu数逐渐上升,到达峰值后(对应圆环射流中的最高速度)再单调下降. 图11 H/D=6时努塞尔数分布图Figure 11 Distribution of Nusselt number at H/D=6 随着同轴射流远离喷嘴出口,因内套管的存在引起的速度分布的双峰效应将消失.反映在冲击传热中则是,冲击高度增加时,Nu数沿径向的分布将单调下降.图11是H/D=6时三个雷诺数下的冲击传热Nu数的模拟结果.可见,此时无论同轴射流的直径比如何变化,Nu数沿径向几乎都是单调下降的(除了Re=28 000时,d/D=0.4、0.27仍略有先升再降的趋势),说明此高度下中心射流与环形射流已经基本充分混合. 冲击高度H/D=3和6的结果均表明,直径比d/D较大的同轴射流(算例一和二),在整个冲击平板范围内的换热效果均优于普通圆柱射流,而直径比变小时(算例三和四),在冲击驻点附近同轴射流传热效果不如圆柱射流,当径向距离r/D>1以后,同轴射流冲击传热效果逐渐优于普通射流.可见,各种射流传热性能的差异主要在冲击驻点附近,且Re数越大越明显. 本文针对几种不同结构参数的同轴射流出口流场及其冲击传热特性进行了数值模拟研究,研究结果表明: 1)与普通圆柱射流不同,由于同轴套管的存在,同轴射流出口附近速度场存在双峰,它在下游会逐渐消失.随着离开喷嘴出口距离的增加,同轴射流的速度分布与喷嘴的几何参数及流动Re数逐渐变得无关. 2)相对于同轴套管的长度而言,同轴射流的直径比是影响流场并进而影响冲击传热特性的主要结构参数.直径比越大,中心射流速度比环形射流速度高出越多,出口速度场双峰也越局限于出口附近;直径比越小,径向速度存在双峰的持续长度就越大. 3)同轴射流的冲击传热特性与速度场密切相关,在冲击驻点附近的传热Nu数受同轴射流的直径比影响很大.直径比较大时有较显著的强化传热效果;直径比较小时,驻点附近同轴射流并没有起到强化传热效果,但在偏离滞止点一定距离后,各种直径比的同轴射流均有一定的强化传热效果.随着冲击高度和离开驻点径向距离的增加,冲击传热性能与直径比之间的依变关系弱化.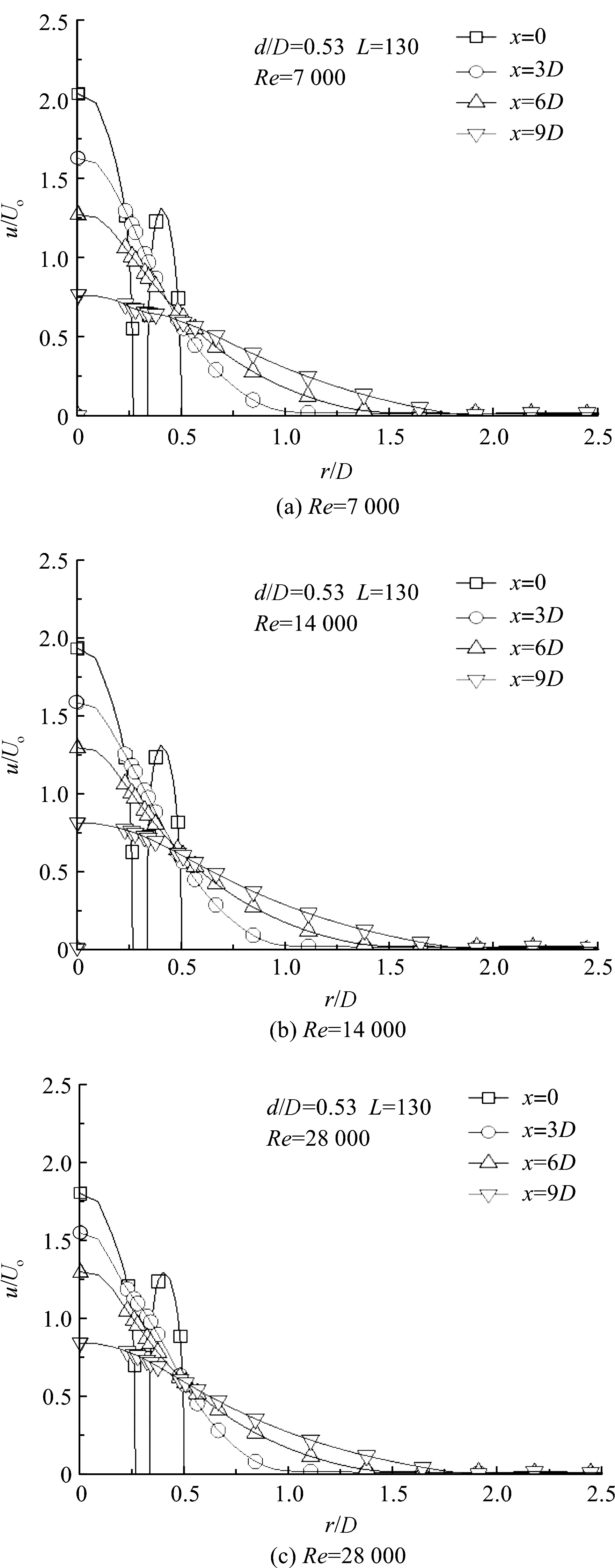

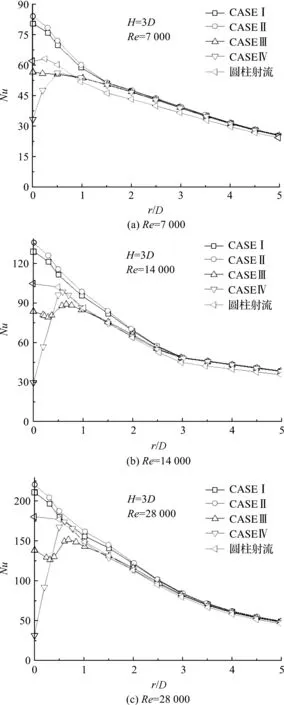
3 冲击传热特性模拟
4 结 论
