利率期限结构与宏观经济的区制依赖关联机制研究

孔小伟

（东莞理工学院 经济管理学院，广东 东莞 523808）

0 引言

传统研究一般认为利率期限结构与宏观经济因素普遍存在线性关联，因而建模大多数从线性模型出发。Diebold等（2006）建立DRA模型研究了美国利率期限结构与其宏观经济的动态关联性，发现宏观经济对收益率曲线的冲击较大，而反向的冲击影响较小。胡永红等（2012）、何小群和王妍（2014）将利率期限结构因素和宏观经济变量引入到状态空间模型中，发现我国利率期限结构与宏观经济之间存在显著的双向关联性。然而，上述线性模型仅仅从总体上反映了期限结构因素与宏观经济因素的对称作用机制，而忽视了宏观经济所处状态对期限结构-宏观经济关系造成的影响，因而对非对称影响机制考虑不足。

基于此，本文从经济状态转变的视角出发，在DRA模型基础上引入马尔科夫区制转移因素，构建宏观-金融MSV-DRA模型，研究利率期限结构与宏观经济非线性动态关系的区制依赖特征，为央行从收益率曲线中提取更加可靠的经济预期信息提供参考依据，以便能及时制定出前瞻性的货币政策，提高政策执行的有效性。

1 模型构建、样本选取和数据说明

1.1 MSV-DRA模型的构建

本文利用Diebold等（2006）建立的DRA状态空间模型，把DRA模型表示为矩阵形式：

观测方程：

状态转移方程：

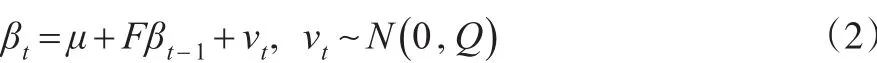
其中，λ是收益率曲线潜在因素的衰减因子，决定了曲率因素到达最大值的时点，H()λ是观测方程的系数矩阵。考虑到产出、通货膨胀和货币政策利率是反映宏观经济动态的三个主要变量，因此将上述DRA模型中的宏观变量集限定为，分别表示经济增长率、通货膨胀率和货币政策利率。

1.2 样本选取与数据说明

（1）收益率数据。选择中央国债登记结算公司基本数据样本，由 14个关键期限包括12、15、18、21、24、30、36、48、60、72、84、96、108、120个月的银行间国债收益率组成，样本期为2002年1月至2014年9月。数据来源于万德数据库。

表1给出了收益率的统计特征。可以发现，我国国债收益率曲线呈现出如下特征：第一，大多数情况下收益率曲线是上倾形状，较少出现平坦情况，只有在极个别的时间出现了下倾；第二，从波动性方面来看，收益率的期限越短，波动越大，期限越长，波动越小；第三，收益率的分布为正偏度，并且随着期限增加而增加，峰度则呈现“U型”特征，先随期限增加而降低，而后随期限增加而上升；第四，收益率的惯性较强，而且长期收益率的惯性稍高于短期收益率；第五，ADF平稳性检验结果显示，在10%的显著性水平内，所有期限的收益率都是平稳序列。

（2）宏观经济数据。宏观经济变量主要选择了经济增长率和通货膨胀率。考虑到GDP只有季度数据，因而以工业增加值ip的月度同比对数代表经济增长率gt，即gt=100*log( )ipt/ipt-12。用物价指数cpi的月度同比对数代表通货膨胀率Inft，即Inft=100*log( )cpit/cpit-12。另外还选择了银行同业隔夜拆借利率rt作为货币政策的代理变量。样本期为2002年1月至2014年9月。上述宏观数据均来源于中经网数据库。

表1 收益率基本统计

采用ADF检验各变量的平稳性，结果显示三个金融变量（Lt、St和Ct）和两个宏观经济变量(gt和Inft)以及货币政策变量rt在10%的统计显著性水平下都不存在单位根，均是平稳序列。

2 模型参数估计及实证检验

2.1 模型估计和判定方法

本文基于MSV-DRA的状态空间模型形式，首先采用Kim滤波并结合卡尔曼滤波、哈密尔顿滤波得到模型的对数似然函数，然后利用极大似然估计方法求解出模型参数，最后再运用卡尔曼滤波结合哈密尔顿滤波得到收益率曲线不可观测的潜在水平、斜率和曲率因素及区制变量。

经计算分析，本文采用MSV-DRA模型描述我国国债利率期限结构与宏观经济变量的非线性动态关系。

2.2 模型估计结果

采用Kim滤波方法所得参数估计结果见表2和表3。可发现收益率曲线因素在区制1的方差高于区制2的方差，表明区制1是高波动状态，区制2是低波动状态。Wald检验结果显示显著拒绝状态变量的协方差矩阵为对角矩阵的零假设，另外也表明了状态变量的协方差矩阵存在区制依赖的异方差性。

表4是MSV-DRA模型的收益率拟合结果，并与单一区制的DRA模型拟合效果进行了对比，总体上反映了MSV-DRA模型对中短期收益率拟合的优越性。

2.3 收益率曲线与宏观经济变量关系检验

收益率曲线三个潜在因素与宏观经济变量之间可能存在三种关系：一是宏观经济变量对收益率曲线存在单向作用；二是收益率曲线对宏观经济存在单向作用；三是二者之间存在双向作用。这三种关系可通过收益率曲线与宏观经济变量间的跨期直接影响和同期扰动相关性来反映。对于特定区制st，上述三种关系可形成三个对应零假设，即H01：F12=0，表示收益率曲线潜在因素对宏观经济变量存在单向影响；H02：F21=Q21=0，表示宏观经济变量对收益率曲线潜在因素存在单向影响；H03：F21=F12=Q21=0，说明收益率曲线潜在因素与宏观经济变量间不存在相互影响。采用Wald检验这三个零假设，所得结果如表5所示，所有零假设都被显著拒绝，表明在两个区制条件下，收益率曲线因素与宏观经济因素间均存在明显的相互影响，这与现有研究结论一致。

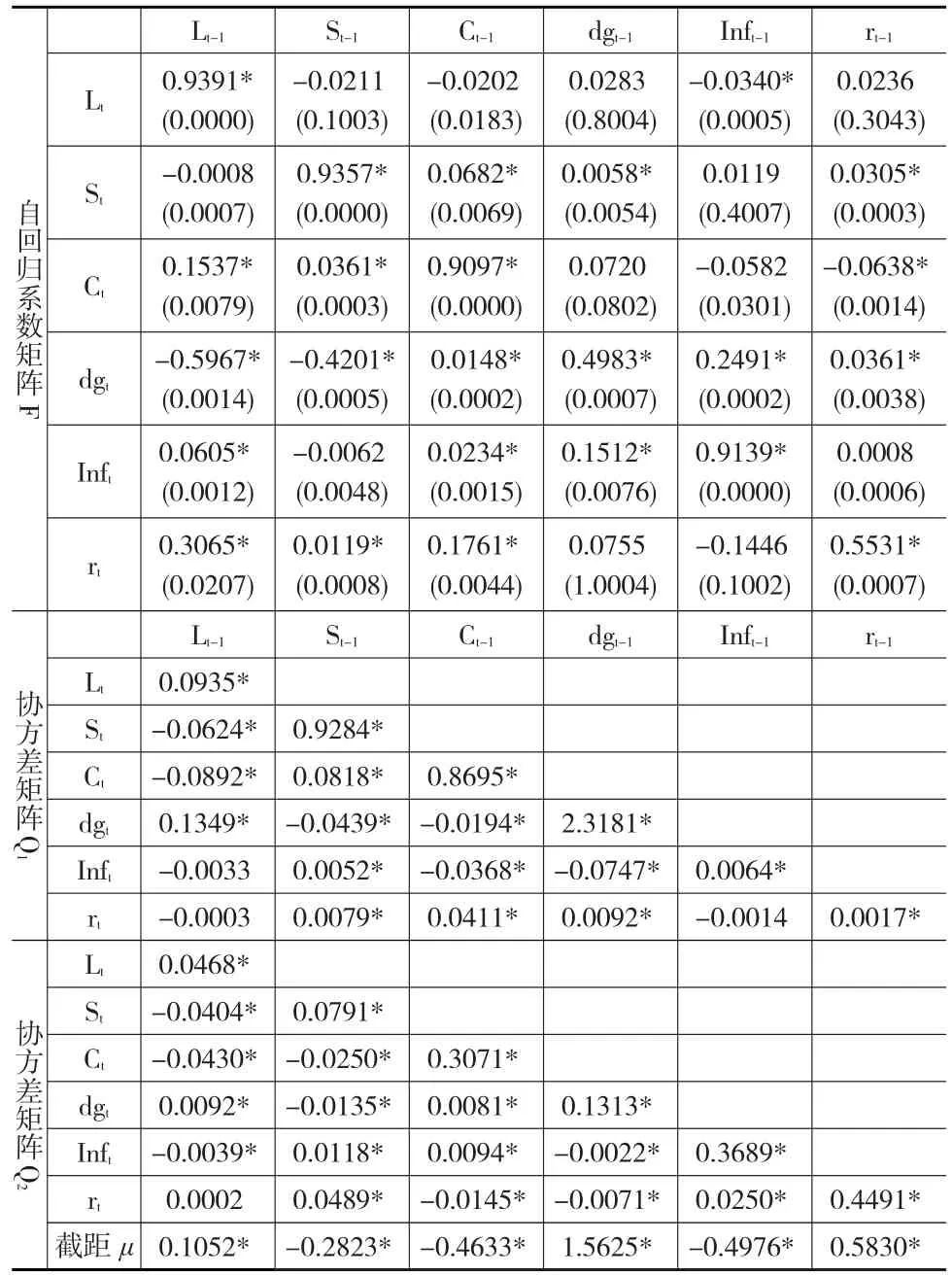
表2 MSV-DRA模型参数估计结果

表3 区制依赖检验结果

表4 模型拟合结果

表5 收益率曲线与宏观经济变量关系的Wald检验结果

2.4 脉冲响应分析

首先，宏观变量对宏观变量冲击的响应基本与货币政策分析中的相关宏观模型所得结果一致，宏观变量具有显著的持续性。在两种区制下，利率上升对通胀的冲击随着时间推移不断增大，但总体上仍较小，这符合一般的货币政策反应函数的特征。而利率的冲击在4个月以后才导致产出的下降。

其次，在区制1条件下，利率对收益率曲线曲率因素的冲击响应为正，并与利率对自身冲击的反应几乎对应，表明在该条件下曲率因素与政策利率的高度相关性，通胀和产出对曲率因素的冲击反应比较微弱；而在区制2条件下，三个宏观因素的响应均为正，且通胀和产出的变化幅度相对较大。对于收益率曲线斜率因素的冲击，产出和通胀的响应在区制1条件下为负且幅度较大，在区制2条件下通胀的初始响应为正，且响应幅度随着时间推移逐渐变小之后转变为负向，直至在第10个月达到负向最大后缓慢下降。此外在区制1条件下，利率对斜率因素冲击的反应比较小，但在区制2条件下几乎是一一对应的，这反映了在该条件下收益率曲线斜率因素与拆借利率的高度关联性。

最后，考察收益率曲线因素对自身冲击的响应。三个潜在因素均存在明显的惯性，水平因素的突然增加，或者说通胀预期的上升与货币政策宽松化密切相关，体现为斜率和曲率因素的下降，使得收益率曲线短端相对于长端降低，收益率曲线变陡峭。另外，水平因素对于斜率和曲率因素的冲击表现出负向反应，斜率因素随着曲率因素的突然增加而增加，而曲率因素对于斜率因素一个标准差冲击的反应则依赖于区制条件，在区制1时曲率因素随着斜率因素的增加而上升，在区制2却随斜率因素的增加而向下跳跃。

2.5 方差分解

表6和表7分别给出了不同区制条件下，期限为12、24和60个月、预测步长为1,12和60个月的收益率方差分解结果。可以看出，收益率的预测误差方差随着预测步长的加大，可由宏观因素解释的比重越来越大，并且在区制1条件下的解释比重总体上高于在区制2条件下的比重，这反映了宏观经济变量是收益率预测的重要考虑因素。

2.6 区制识别

假设短期利率动态服从泰勒规则，把收益率曲线水平因素看成中期通胀目标，通胀缺口表示为Gapπ，t=Inft-Lt，把经H-P滤波调整的产出缺口表示为GapIP，t，分高、低两个区制分别进行回归得到：

表6 区制1条件下的方差分解

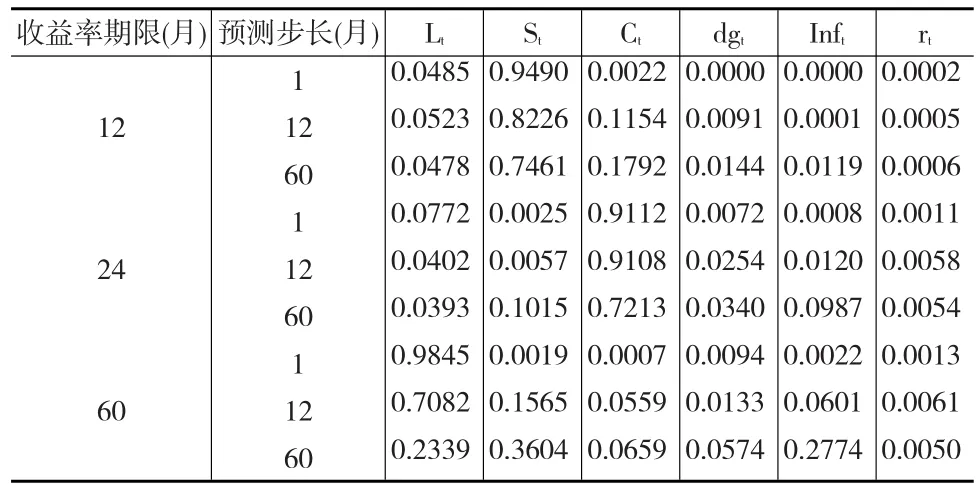
表7 区制2条件下的方差分解

括号内为t值。可见大多数回归系数都是显著的，在高波动区制的通胀缺口系数小于低波动区制的系数，反映了央行在低波动区制更加重视对通胀水平的控制。高波动区制的产出缺口系数高于低波动区制的系数（不显著），说明央行在高波动区制更加强调经济增长。上述泰勒规则的回归结果表明MSV-DRA模型的两个高低波动区制可以理解为货币政策的宽松和紧缩两种状态。

3 结论

本文基于DNS模型的拓展思路，在DRA模型中引入马尔科夫区制转移变量，构建两区制的宏观-金融MS-DRA模型，并通过运用卡尔曼滤波、哈密尔顿滤波和Kim滤波相结合的方法求解模型参数，最终获得收益率曲线潜在因素和系统区制转移路径。得到如下主要结论：

第一，从模型拟合效果和模型区制依赖检验结果来看，两区制的MSV-DRA模型比传统单一区制DRA模型更适合描述我国国债收益率曲线与宏观经济的非线性动态关联机制；上述结果均反映了国债利率期限结构-宏观经济关系存在区制依赖特征，因此决策层在运用国债收益率曲线进行政策制定时，把宏观经济所处的状态纳入考虑范围是有益和必要的。

第二，模型自回归系数矩阵检验结果显示收益率曲线与宏观经济之间存在显著的双向影响，而方差分解结果表明宏观经济因素在高波动区制下对收益率预测方差的解释比重高于在低波动区制下的解释比重，反映了宏观经济变量和区制状态都是收益率预测的必要考虑因素。

第三，对MSV-DRA模型的两个区制进行识别，发现其高低波动区制可以分别理解为货币政策的宽松和紧缩状态，因此我国银行间国债利率期限结构与宏观经济的非线性动态关联机制表现出货币政策状态依赖特征。