A Real-Valued 2D DOA Estimation Algorithm of Noncircular Signal via Euler Transformation and Rotational Invariance Property
2018-07-11ChenXueqiangWangChenghuaZhangXiaofei
Chen Xueqiang,Wang Chenghua,Zhang Xiaofei
1.Key Laboratory of Radar Imaging and Microwave Photonics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China;
2.College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China
Abstract:The problem of two-dimensional(2D)direction of arrival(DOA)estimation for double parallel uniform linear arrays is investigated in this paper.A real-valued DOA estimation algorithm of noncircular(NC)signal is proposed,which combines the Euler transformation and rotational invariance(RI)property between subarrays.In this work,the effective array aperture is doubled by exploiting the noncircularity of signals.The complex arithmetic is converted to real arithmetic via Euler transformation.The main contribution of this work is not only extending the NC-Euler-ESPRIT algorithm from uniform linear array to double parallel uniform linear arrays,but also constructing a new 2D rotational invariance property between subarrays,which is more complex than that in NCEuler-ESPRIT algorithm.The proposed 2D NC-Euler-RI algorithm has much lower computational complexity than 2D NC-ESPRIT algorithm.The proposed algorithm has better angle estimation performance than 2D ESPRIT algorithm and 2D NC-PM algorithm for double parallel uniform linear arrays,and is very close to that of 2D NC-ESPRIT algorithm.The elevation angles and azimuth angles can be obtained with automatically pairing.The proposed algorithm can estimate up to 2(M-1)sources,which is two times that of 2D ESPRIT algorithm.Cramer-Rao bound(CRB)of noncircular signal is derived for the proposed algorithm.Computational complexity comparison is also analyzed.Finally,simulation results are presented to illustrate the effectiveness and usefulness of the proposed algorithm.
Key words:array signal processing;direction of arrival(DOA)estimation;noncircular signal;Euler transformation
0 Introduction
The problem of estimating the direction-ofarrival(DOA)of multiple sources in the field of array signal processing has received considerable attention for decades[1-3].Various DOA estimation algorithms have been developed and applied in many fields,including mobile communication system,radio astronomy,sonar and radar[4-6].Although the maximum likelihood estimator[7-8]provides the optimum parameter estimation performance,its computational complexity is extremely high.Suboptimal but simpler solutions can be achieved by subspace based approaches,which rely on the decomposition of observation space into signal subspace and noise subspace.For example,both multiple signal classification(MUSIC)method[9]and estimation of signal parameters via rotational invariance technique(ESPRIT)[10]are well-known subspace based directions of arrival estimation algorithm for their good angle estimation performance.
Noncircular signals have received considera-ble attention in the field of spatial spectrum estimation[11].The amplitude modulation(AM)and binary phase shift keying(BPSK)modulated signals frequently used in communication systems are noncircular(NC)signals[12].The noncircularity of signal is investigated to enhance the performance of angle estimation algorithm by combing array output and its conjugated counterpart.Some noncircular DOA estimation methods of multiple signals have been reported,such as NCMUSIC algorithm[13],NC-ESPRIT algorithm[14],NC-propagator methods(NC-PM)[15-16],and NC-parallel factor(NC-PARAFAC)algorithm[17].These noncircular DOA estimation algorithms have better angle estimation performance and can estimate more sources.
However,the arithmetic of the above mentioned DOA estimation algorithms is operated in complex field.Thus the corresponding computational complexity is very high.Huarng and Yeh have proposed real-valued MUSIC algorithm[18]and real-valued ESPRIT algorithm[19]by unitary transformation,respectively.A real-valued noncircular ESPRIT algorithm for uniform linear array has been proposed in Ref.[20],which has lower computational complexity than NC-ESPRIT[14]algorithm.Then this method is extended to PM algorithm for two-dimensional(2D)angle estimation by Zhang[21].
In this paper,a computationally efficient 2D angle estimation algorithm of noncircular signal for double parallel uniform linear arrays via Euler transformation and rotational invariance property between subarrays(2D NC-Euler-RI)is proposed.The complex arithmetic in this work is converted to real arithmetic by Euler transformation.The main contribution of this work is not only extending the NC-Euler-ESPRIT algorithm[20]from uniform linear array to double parallel uniform linear arrays,but also constructing a new 2D rotational invariance property between subarrays,which is more complex than that in NC-Euler-ESPRIT algorithm.Moreover,the proposed 2D NC-Euler-RI algorithm needs to consider matching problem between elevation angles and azimuth angles.We also analyze the computational complexity of the proposed algorithm and derive the CRB of noncircular signal for double parallel uniform linear arrays.
The proposed algorithm has the following advantages:(1)It has lower computational complexity than 2D ESPRIT[10]algorithm and 2D NCESPRIT algorithm[14]for double parallel uniform linear arrays.(2)It can estimate up to 2(M-1)sources,which is two times that of NC-Euler-ESPRIT algorithm.(3)It can achieve automatically paired elevation angles and azimuth angles.(4)It has better angle estimation performance than that of 2D ESPRIT algorithm[10],2D NC-PM algorithm[22]for double parallel uniform linear array,and close to that of 2D NC-ESPRIT algorithm[14].
Notations:(·)-1,(·)*,(·)T,(·)H,(·)+denote inverse,conjugate,transpose,conjugate-transpose and pseudo-inverse operations,respectively.diag{v}stands for a diagonal matrix,whose diagonal elements are the elements in vector v.IKis a K×K identity matrix.E(·)is the expectation operator.angle(·)means to get the phase.Re[·]and Im[·]mean to get the real part and imaginary part of complex number,respectively.
1 Data Model
Assume that there are K uncorrelated narrowband sources impinging on double parallel uniform linear arrays,and each uniform linear subarray equipped with M sensors is shown in Fig.1.The distance d between adjacent sensors is equivalent to half of the wavelengthλ.The sources are far away from the subarrays,thus the incoming waves over the sensors are essentially planes.The noise is additive independent identically distributed Gaussian with zero mean and varianceσ2,which is uncorrelated with the signal.We denote the 2D DOAs of k th source asφk=[θk,φk],whereθkandφkdenote elevation angle and azimuth angle,respectively,and k=1,…,K.
The output signals of subarrays along X axis at time t can be modeled as[23]

where x1(t),x2(t)∈CM×1are the received signals of each subarray;A=[a1,…,ak,…,aK]∈CM×Kis the steering matrix,ak=[1,…,ej(m-1)τx,k,…,ej(M-1)τx,k]T,τx,k=2πd·cos(φk)sin(θk)/λ,m=1,…,M;s(t)∈CK×1;andΦYis a diagonal matrix

whereτy,k=2πd sin(φk)sin(θk)/λ.
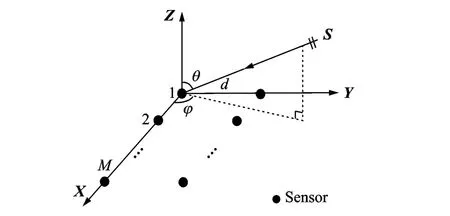
Fig.1 Array geometry[23]
A brief definition of noncircular signal is given in the following[24].Let s(t)be a complex random process with zero mean.The second order statistics of s(t)are defined as the covariance E{s(t)s*(t)}and conjugate covariance E{s2(t)},respectively.The relationship between these two covariance measures is

whereψis the noncircular phase andρ(ρ∈[0,1])denotes the noncircular rate.It is defined that s(t)is circular whenρ=0 and is noncircular when 0<ρ≤1.
Only the signals of maximum noncircular rateρ=1 are considered in this work.The noncircular signals s(t)with maximum noncircular rate can be expressed as

where s0(t)∈RK×1,and

whereψkis the noncircular phase of k th signal and is assumed to be in the range of[0,π].
2 Angle Estimation Algorithm
2.1 Euler transformation of array output
According to Eq.(1),define the real-valued subarray output via Euler transformation[20]as follows

where A1c,A1s,A2c,A2c∈ RM×K,n1c(t)=Re[n1(t)],n1s(t)=Im[n1(t)],n2c(t)=Re[n2(t)],n2s(t)=Im[n2(t)].
Construct the extended real-valued array output as

with L snapshots can be written as

where Xr∈R4M×L,S0∈RK×L,Nr∈R4M×L.
2.2 2D NC-Euler-RI algorithm
Define

where T1and T2∈R(M-1)×M.
Let
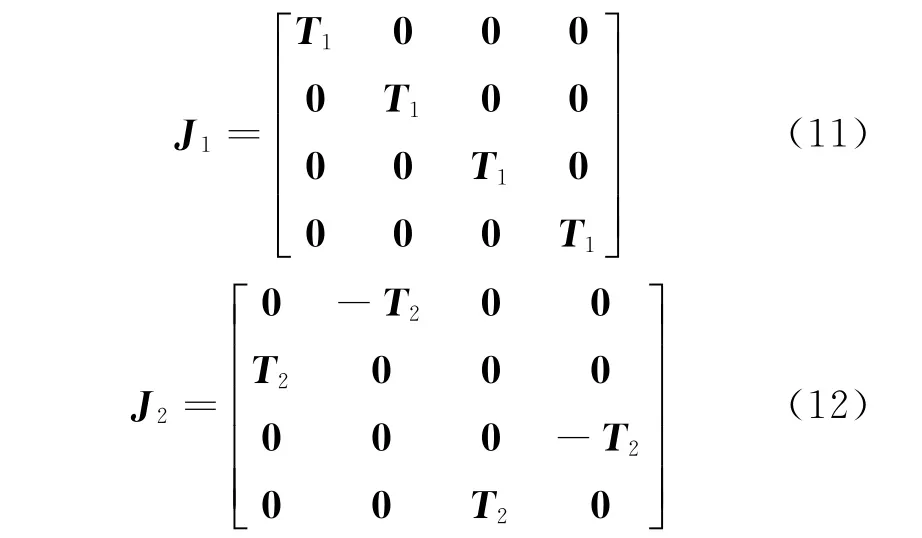
where J1,J2∈R4(M-1)×4M.
Combining Eq.(7)and Eqs.(11),(12),we have
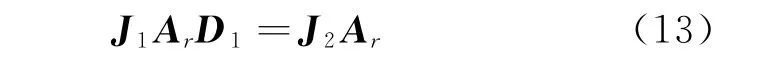
where

where D1∈RK×K.
Define the covariance matrix of xr(t)as[25]

where Rx∈R4M×4M,R0=E[s0(t)sT0(t)]∈RK×K.
Rxcan be rewritten via Eigen value decomposition(EVD)as

where Us∈R4M×K,Un∈R4M×(4M-K),Σs∈RK×K,
For Usand Arcan span the same signal subspace,it can be obtained that

whereΠ1is a nonsingular matrix,andΠ1∈RK×K.
Combine Eq.(13)and Eq.(17),and we have

Define

where P1∈RK×K.
According to Eqs.(18),(19),we have

Perform the EVD of P1,which can be expressed as

where V∈RK×K,γkis the k th diagonal element ofΛ.
Combine Eq.(14)and Eqs.(20),(21),and we have

Then reconstruct the extended real-valued array output data along Y axis as

where yr(t),ny(t)∈R4M×1,Br∈R4M×K,and


where dm,k=(m-1)τx,k,Dm,k=dm,k+τy,k.
Define

Let

Combine Eqs.(29),(30)and construct J3,J4as follows

where J3,J4∈R2M×4M.
Combine Eq.(23)and Eqs.(31),(32),and we have

where D2∈RK×K,and

Define the covariance matrix of yr(t)as[25]

where Ry∈R4M×4M.
Rycan be rewritten via EVD as

where Bs∈R4M×K,Bn∈R4M×(4M-K),Δs∈RK×K,
For Bsand Brcan span the same signal subspace,it can be obtained that

whereΠ2∈RK×Kis a noncircular matrix.
Combine Eq.(33)and Eq.(37),and we have

Define

where P2∈RK×K.
According to Eqs.(38),(39),we have

Perform the EVD of P2,which can be rewritten as

whereΗ∈RK×K,,ωkis the k th diagonal element ofΩ.
Combining Eqs.(40),(41),it can be obtained that

Note that the EVDs of P1and P2are performed,respectively.We should consider the column ambiguity and scale fuzzy betweenΛandΩ before estimating the DOAs.According to Eqs.(7),(23),yr(t)can be obtained by row elementary transformation of xr(t),so Bscan be achieved as follow

where J0is the row elementary transformation matrix.
Then replaceΠ2in Eq.(40)with

The column ambiguity and scale fuzzy betweenΛ andΩcan be solved.
Define that

Thus the estimates ofμkandηkare

Therefore,the azimuth angles and elevation angles can be estimated as follows

2.3 Algorithm description
The implementation of the proposed algorithm with finite array output data is summarized in this section.The sampled covariance matriceswith L snapshots are defined as[26]

The procedure of the proposed 2D NC-Euler-RI algorithm for double parallel uniform linear arrays is presented in the following.
(1)Initialize the sampled array output data of subarrays X1,X2,and define the matrices J0,J1,J2,J3,J4.
(2)Construct the extended real-valued array output Xrvia Euler transformation.
(3)Compute the corresponding sampled covariance matrix^Rx,and perform the EVD of^Rx.
(4)Extract the signal subspace Us,and reconstruct Usto get Bsvia Eq.(43).
(5)Compute the matrices P1and P2,and perform the EVD of P1and P2,respectively.
(6)Estimate the elevation angles and azimuth angles via Eqs.(49),(50).
Remark 1 It is assumed that the number of sources is pre-known,or it can be estimated by some methods shown in Refs.[27-29].
Remark 2 The column ambiguity and scale fuzzy betweenΛandΩare solved via Eqs.(47),(48).Thus the elevation angles and azimuth angles can be obtained with automatic pairing.
2.4 Analysis of complexity
Regarding the computational complexity,only matrix multiplication operations are considered.The complexities of 2D ESPRIT algorithm[10],2D NC-ESPRIT algorithm[14]and the proposed 2D NC-Euler-RI algorithm for double parallel uniform linear arrays are analyzed in Table 1.Fig.2 is the simulation results of computational complexity comparison among 2D ESPRIT algorithm,2D NC-ESPRIT algorithm and 2D NC-Euler-RI algorithm with different numbers of snapshots L and sensors M.It can be seen that the proposed 2D NC-Euler-RI algorithm hasmuch lower computational complexity of than that of 2D NC-ESPRIT algorithm,and close to that of 2D ESPRIT algorithm.

Table 1 Computational complexity of three methods for double parallel uniform linear arrays

Fig.2 Simulation results of complexity comparison with different values of L and M
Note that the dimension of array output data is doubled by exploiting the noncircularity of signal.The effective array aperture of the proposed algorithm is 2M,which is two times that of ESPRIT algorithm.Thus the proposed algorithm can estimate up to 2(M-1)sources.
3 Cramer-Rao Bound
We derive the CRB of noncircular signals for double uniform linear arrays in this section.There are some differences between the CRB of noncircular signals DOA estimation and that of circular signals DOA estimation[17].The parameters needed to estimate can be defined as

where sR(tl)and sI(tl)denote the real and imaginary parts of s(tl),respectively.
According to Eq.(1),the sampled array output with L snapshots can be rewritten as

The meanμand covarianceΓof z are

From Ref.[30],the(i,j)element of the CRB matrix P can be expressed as

whereμ′iandΓ′idenote the first-order derivative ofμandΓwith respect to the i th element ofζ,respectively.
For the covariance matrixΓis just related to σ2,the first term of Eq.(56)can be ignored.The(i,j)element of CRB matrix P can be simplified as

According to Eqs.(52,54),we have

where sk(tl)is the k th element of s(tl),and
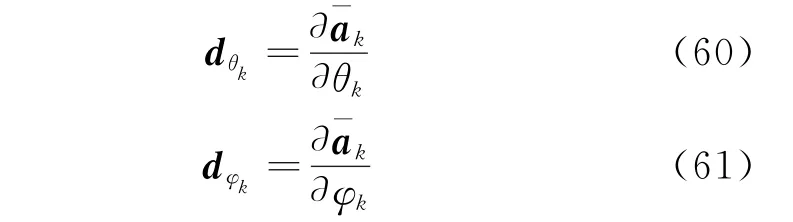
Define

where

Then we have


Combining Eq.(52)and Eqs.(62)—(67),the first-order derivative ofμwith respect toζis
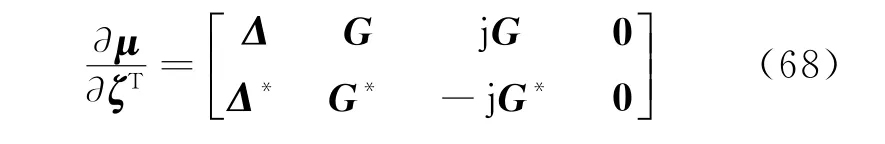
Combine Eq.(55)with Eq.(68),and Eq.(57)can be rewritten as

where

Let

where BRand BIare the real and imaginary parts of B,respectively.
According to Eqs.(69)—(71),we have

Thus,it can be demonstrated that

Only the elements related to the angles are considered.According to Eq.(74),J-1can be expressed as


whereκdenotes the parts unrelated to the elevation angles and azimuth angles.
Thus,the CRB matrix can be obtained as

After further simplification,the CRB matrix can be rewritten as

4 Simulation Results
The Monte Carlo simulations are adopted to evaluate the angle estimation performance of the proposed algorithm.The rootmean square error(RMSE)is defined as[31]

In the following simulation results except Figs.4,7,8,we assume that there are K=3 sources located at angles of(θ1,θ2,θ3)=(15°,35°,55°)and(φ1,φ2,φ3)=(10°,30°,50°).The noncircular phases are(ψ1,ψ2,ψ3)=(20°,40°,60°),respectively.
Fig.3 presents angle estimation result of elevation angles and azimuth angles of the proposed algorithm.M=8 and L=300 are used in the simulations,while SNR=10 dB.From Fig.3,the elevation angles and azimuth angles can be clearly observed.

Fig.3 Angle estimation result over Monte Carlo simulations
Fig.4 shows the angle estimation performance comparison among the proposed algorithm,2D ESPRIT algorithm[10],2D NC-ESPRIT algorithm[14],2D NC-PM algorithm[22],and CRB of noncircular signals for double parallel uniform linear arrays.M=6,K=2 and L=300 are used in the simulations.From Fig.4,it is indicated that the angle estimation performance of the proposed algorithm is close to that of 2D NC-ESPRIT algorithm and better than that of the other 2D angle estimation algorithms,since the effective array aperture is doubled by exploiting the noncircularity of signals.
Fig.5 shows angle estimation performance of the proposed algorithm with L=300 and different values of M.From Fig.5,it can be seen that the increasing of M will lead to the improvement of angle estimation performance of the proposed algorithm.
Fig.6 depicts angle estimation performance of the proposed algorithm with M=8 and different values of L.From Fig.6,the angle estimation performance of the proposed algorithm is enhanced with the number of snapshots increasing.
Fig.7 presents angle estimation performance of the proposed algorithm with M=8,L=300 and different values of K.From Fig.7,it can be found that the angle estimation performance of the proposed algorithm degrades with the number of source increasing.
Fig.8 displays the simulation result of the proposed algorithm with two closely spaced sources.In Fig.8,we assume that the two closely spaced sources are located at angles of(θ1,θ2)=(30°,32°)and(φ1,φ2)=(10°,12°).The corresponding noncircular phases are(ψ1,ψ2)=(20°,40°),respectively.M=10,L=500 and SNR=20 dB are used in the simulation.Fig.8 implies that the proposed algorithm works well when two sources are closely spaced.
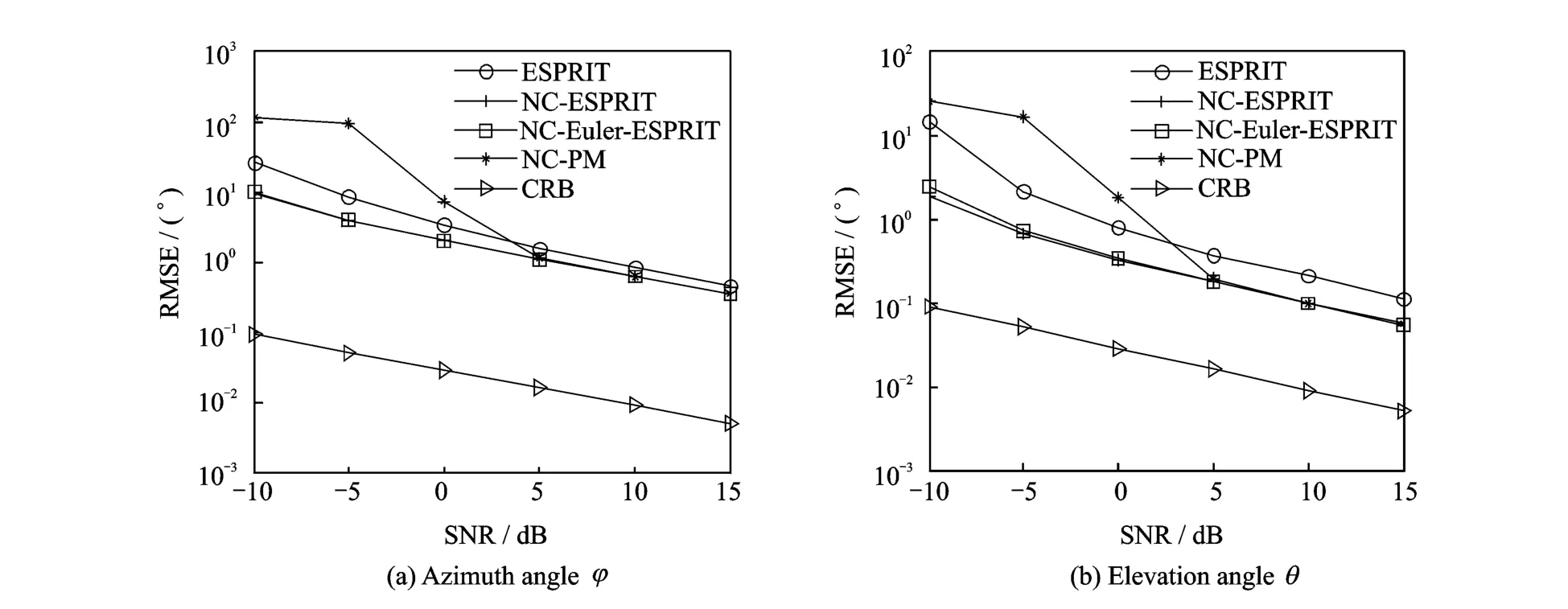
Fig.4 Simulation results of angle estimation performance comparison

Fig.5 Angle estimation performances with different values of M

Fig.6 Angle estimation performances with different values of L

Fig.7 Angle estimation performances with different values of K

Fig.8 Angle estimation result of two closely spaced sources
5 Conclusions
In this paper,we have proposed a real-valued 2D NC-Euler-RI algorithm of noncircular signals for double parallel uniform linear arrays.The proposed algorithm has the following advantages:
(1)It has much lower computational complexity than that of 2D NC-ESPRIT algorithm[14]for double parallel uniform linear arrays.
(2)It has better angle estimation performance than that of 2D ESPRIT algorithm[10]and 2D NC-PM algorithm[22]for double parallel uniform linear arrays,and very close to that of 2D NC-ESPRIT algorithm[14]for double parallel uniform linear arrays.
(3)It can estimate elevation angles and azimuth angles with automatically pairing.
(4)The maximum number of source estimated by the proposed algorithm is two times that of 2D ESPRIT algorithm,for the effective array aperture is doubled via utilizing the noncircularity of signal.
We also analyze the computational complexity of the proposed algorithm.The CRB of noncircular signals for double parallel uniform linear arrays are also derived.It is well known that CRB expresses a lower bound on the variance of an unbiased estimator,which can be used to compare the angle performance of different algorithms.From Fig.4,it can be seen that the RMSE of the proposed 2D NC-Euler-RI algorithm is much closer to CRB compared with that of 2D ESPRIT algorithm and 2D NC-PM algorithm.It is also clearly indicated that the angle estimation performance of our algorithm is better than that of 2D ESPRIT algorithm and 2D NC-PM algorithm.Finally,the angle estimation performance and computational complexity of the proposed algorithm are evaluated by numerical simulations.Simulation results illustrate the effectiveness of the proposed algorithm in a variety of scenarios,even when the sources are closely spaced.
Acknowledgements
This work is supported by the National Science Foundation of China(No.61371169)and the Aeronautical Science Foundation of China(No.20120152001).
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Arnoldi Projection Fractional Tikhonov for Large Scale Ill-Posed Problems
- SEM-Based Method for Performance Evaluation of Wired LANs
- High-Order Discontinuous Galerkin Solution of Compressible Flows with a Hybrid Lattice Boltzmann Flux
- Experiment on a Double-Foot Stepping Piezoelectric Linear Motor
- Structural and Piezoelectric Properties of Sr0.6Ba0.4Nb2O6Micro-rods Synthesized by Molten-Salt Method
- Multilevel Characteristic Basis Function Method with ACA for Accelerated Solution of Electrically Large Scattering Problems
