一种基于压缩感知的全变分图像去噪算法
2018-07-10刘泽鹏陈媛媛
刘泽鹏,陈媛媛
(1. 中北大学 光电信息与仪器工程工程研究中心,山西 太原 030051;2. 中北大学 信息与通信工程学院,山西 太原 030051)
0 引 言
随着科学技术的发展,人们对于图像质量的要求越来越高,然而,大部分获得的图像由于噪声的存在,其质量往往达不到人们的要求. 噪声降低了图像的质量,使得人们不能有效的获取到图像中的信息,也给图像的后续处理带来各种困难. 因此,需要一种快速且有效的方法来去除图像中的噪声.
传统的图像去噪方法有空域和频域两大类,其工作思想主要是基于图像的有效信息和噪声频率特性的差别来去除噪声. 空域去噪的方法主要包括均值滤波、高斯滤波、中值滤波和维纳滤波法等,该类方法的主要缺点是不能很好地保留图像的边缘信息,降噪后的图像质量视觉较差; 频域去噪方法主要是通过对含有噪声的图像进行各种变换,例如小波变换、小波包变换等,从而进行降噪,该类方法虽然降噪效果优于空域法,但效果不稳定,算法的设计比较复杂.
本文将压缩感知[1-4]理论运用到图像去噪过程,利用压缩感知中的算法对图像进行重构和噪声去除. 目前,常用的重构算法[5]主要分为两大类: 基于L1范数的凸优化算法和基于L0范数的贪婪算法. 凸优化算法的重构思想是通过添加约束项来逼近最优解,主要算法包括基追踪(basic pursuit,BP)、全变分(total variation, TTV)等; 贪婪算法的重构思想是通过选择合适的原子并通过一系列迭代实现信号的原始逼近,该类算法主要包括匹配追踪(orthogonal matching pursuit,MP)、正交匹配追踪(orthogonal matching pursuit,OMP)、压缩采样匹配追踪(compressive sampling orthogonal matching pursuit,CoSaMP)以及子空间追踪(subspace pursuit,SP)等. 对比两种算法,基于L0范数的贪婪算法虽然重构速度优于凸优化算法,但是其重构精度没有凸优化算法高,而且随着凸优化算法的改进,其部分算法的重构速度已不亚于贪婪算法. 近年来,众多学者基于压缩感知对图像去噪提出了各种方法[5-12],取得了不错的效果. 本文采用全变分[13]算法中的TVAL3算法对含噪图像进行去噪,通过实验仿真,表明本文的算法优于其它压缩感知算法.
1 压缩感知基本理论
2006年,美国科学家Donoho、Candès和Tao等人提出压缩感知[1-4](compressed sensing, CS)理论,理论指出,假如信号本身是可压缩的或在某个变换域是稀疏的,那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上,然后,通过求解一个最优化问题就可以从低维空间以高概率重构出原信号.
假设x∈RN的一维信号,可以通过某个稀疏基φ=[φ1,φ2,…,φN]对信号进行稀疏表示,信号x∈RN在基φ下的表示为
(1)
式中: 当向量θ中绝对值较大的元素很少,则可以认为θ是稀疏的或者是可压缩的. 如果向量θ中只有K个元素值不为零,其它元素值都为零,则称θ为K稀疏信号(严格稀疏),其中K≪N.
通过一个与稀疏基不相关的测量矩阵Φ对信号x∈RN进行测量,测量矩阵Φ∈RM×N(M≪N),可以得到测量向量y. 式(2)为信号x经过测量矩阵Φ得到测量向量y的过程.
y=Φx=Φφθ=Aθ,
(2)
式中:A为传感矩阵,也叫CS信息算子,A∈RM×N,y∈RM,为测量值. 对于给定的y,从式(2)可求出θ是一个线性规划问题,但由于M≪N, 即方程的个数远小于未知数的个数, 是一个欠定性问题, 一般来讲无确定解,因此重构过程是一个NP难问题. 对此,Candès和Tao研究并证明了如果传感矩阵A满足有限等距性质(RIP)[14,15],在某种意义来说,等同于测量矩阵Φ和稀疏基φ不相关.
定义1(RIP)对于矩阵A∈RM×N,若对任意θ∈RI和常数δ∈(0,1), 如果
(1-δ)‖θ‖2≤‖AIθ‖2≤(1+δ)‖θ‖2
(3)
成立,其中θ为K稀疏信号,I⊂{1,2,…,N},︱I︱≤K,AI表示由索引集合I⊂{1,2,…,N}在A中列向量构成的子矩阵,则称矩阵A满足有限等距性(RIP). 通常称使得式(3)成立的参数δ的最小值为有限等距常数(RIC),记为δm.
式(2)中的θ可以求解L0最小范数而精确重构,重构公式为
min‖θ‖0s.t.y=Aθ.
(4)
由于式(3)是一个非凸优化问题,求解是一个NP难问题. 由此转化为求解L1最小范数问题,重构公式为
min‖θ‖1s.t.y=Aθ.
(5)
式(4)为一个凸优化问题,于是可以化简为线性规划问题,求解该问题典型的算法为凸优化算法,凸优化算法是将非凸优化问题转化为凸优化问题进而求解,如基追踪(BP)算法、梯度投影方法和全变分(TV)算法等.
2 基于TVAL3的图像去噪
2.1 TVAL3重建算法
TVAL3[5]算法以全变分正则化模型为基础,采用增强拉格朗日(augmented lagrangian method)和交替方向变换(alternating direction method)求解目标函数. 该方法速度快,重建质量高,而且灵活性好,支持多种测量矩阵和约束条件.
TVAL3算法模型为全变分正则化(total variation regularization),即
(6)
式中:A为测量矩阵;u为输入的原始图像;i和j表示图像的行与列;b为测量值;Diu表示图像的变分或梯度值. 其中图像的全变分公式为
(7)
采用拉格朗日方法将目标函数等价于
(8)
引入松弛变量w,模型变成
(9)
目标函数则变成

(10)
通过引入松弛变量和增广拉格朗日方法,目标函数转变为
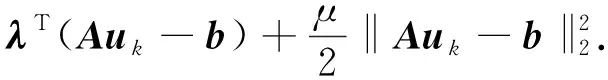
(11)
采用交替方向变换方法,可以将问题转变为求解两个子问题,即求w和u,通过迭代方法首先求解w,再求u.
w的子问题为
(12)
u的子问题为
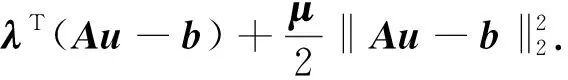
(13)
采用交替最小化法求解式(10),获得
uk+1=uk-αkdk,
其中,
根据公式,对于所有的i, 有
vi←vi-β(Diui-wi),
λ←λ-μ(Aui-b).
2.2 压缩感知的去噪图像模型
本文所处理加性高斯白噪声的含噪图像的模型为
y=x+n,
(14)
式中:y为含噪图像;x为清晰图像;n为加性噪声. 首先根据压缩感知理论,对含噪图像进行稀疏表示,即
y=x+n=φs,
(15)
式中:φ为对含噪图像采用的稀疏基. 然后对含噪图像进行观测测量,为
Y=X+N=ΦS.
(16)
最后,通过TVAL3算法求解一个最优化问题进行图像的重构和去噪,即
(17)
通过求解式(17)的最小目标函数来估计清晰图像的稀疏表示,然后恢复重建图像,从而去除噪声.
3 实验结果与分析
实验仿真所用的环境为Intel(R) Core(TM) i5-4200U CPU @1.60GHz 2.30 GHz 4.00GBRAM Window7.32bit MATLAB 7.11.0(2010b). 实验采用256×256的Albert.Einstein作为原始图像,对原始图像添加均值为0,方差为0.005的加性高斯白噪声作为含噪图像,采用离散小波变换(DWT)对含噪图像进行稀疏化处理,选取高斯随机矩阵作为测量矩阵Φ∈RM×N. 为了说明本文算法的重构效果,将本文算法与其它压缩感知的重建算法OMP和SP进行对比,最后对三种算法的峰值信噪比(peak signal to noise ratio,PSNR/dB)和重构时间(t/s)进行了对比分析.
(18)
式中:I(i,j)为原始图像像素值;I′(i,j)为恢复图像像素值;I(i,j)max表示图像颜色的最大数值,8 bit图像取值最大为255.
在采样率分别为0.4和0.8时,通过利用本文重建算法与其它对比的压缩感知重建算法OMP和SP进行实验仿真对比,重构结果对比如图 1 和图 2 所示.

图 1 采样率为0.4时三种算法的重建图像Fig.1 The reconstructing image of the three algorithms at a sampling rate of 0.4

图 2 采样率为0.8时三种算法的重建图像Fig.2 The reconstructing image of the three algorithms at a sampling rate of 0.8
图 1 和图 2 中,(a)是原始图像,(b)是添加均值为0,方差为0.005的加性高斯白噪声含噪图像,(c)是三种算法各自恢复的图像. 对比上述的恢复图像及三种算法的PSNR和重构时间,可以看出,采样率越高,图像的恢复效果越好. 可见本文算法在重构性能上明显优于其它两种对比的压缩感知重建算法. 而且随着采样率的提高,本文算法的重建时间缩短,原因是由于采样率提升,TVAL3算法求解所需的迭代次数减少,在采样率为0.4时,TVAL3算法所需的迭代次数为78次,但采样率在 0.8 时,TVAL3算法的迭代次数减少到57次,所以所需时间变短.
综上所述,通过实验仿真的重构效果和数据对比可知,本文采用的TVAL3算法对含噪图像的重构效果和噪声去除明显优于对比的压缩感知算法,使得重构图像的效果越来越好,重构时间变短.
4 结 语
本文针对传统图像去噪的不足,采用了一种基于压缩感知的图像去噪方法,该方法以全变分正则化为模型,采用增强拉格朗日和交替方向变换求解目标函数的最优解. 通过实验仿真表明,该方法能够很好地进行图像重构和噪声去除,在含噪图像的重构效果和噪声去除方面明显优于对比的压缩感知算法.
