基于原子轨道基的实时密度泛函理论:方法及应用∗
2018-07-10关梦雪1廉超1孟胜1
关梦雪1) 廉超1) 孟胜1)2)†
1)(中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)
2)(量子物质科学协同创新中心,北京 100190)
(2018年3月19日收到;2018年4月17日收到修改稿)
1 引 言
实时演化的含时密度泛函理论[1,2](realtime time dependent density functional theory,rt-TDDFT)中,电子密度由时间依赖的Kohn-Sham(time-dependent Kohn-Sham,TDKS)方程数值积分得到,可以直接在非微扰的情况下提供电子波函数的时域演化动力学,结合原子核的运动,能够直观地给出电子-原子核多体量子体系随时间的演化路径.因此,rt-TDDFT已成为计算模拟强场物理、超快物理过程的最有效的工具之一[3−8].
目前,rt-TDDFT的应用范围已经从原子分子体系拓展到凝聚态物质中,其数值实现大多基于平面波[9]或者实空间网格点方法[10,11].然而,在以上的两种方法中,如果要研究能量尺度在10—100 eV的高能电子激发,则需要包含很高能量的平面波基矢或者很密集的网格点才能准确地描述i原子内层电子的运动.同时,对于一个有Na个原子的体系,计算所需的基矢数目高达103Na—104Na,因此无法进行有效的大规模模拟.这些因素都将显著提高计算成本,并大大限制了rt-TDDFT理论的应用范围.
鉴于上述现状,我们发展了一套基于数值原子轨道基的rt-TDDFT计算方法以及软件TDAP(Time Dependent Ab initio Package)[12,13].相较于平面波和实空间展开,用基于数值化局域原子轨道的基矢展开波函数,要求较少的基数目就可以很好地描述系统的电子态信息,大幅减小了计算量.另外,由于局域轨道只在有限空间分布,在此空间之外严格为零,所以对于大体系只有该空间内的原子会有波函数的重叠,哈密顿量为准线性,使得我们能够获得计算量随尺寸成线性增长的好处.利用TDAP,能够长时间地模拟大尺寸系统的动力学演化过程,其计算成本较于平面波和实空间网格点方法大幅降低,并且能够保持很高的精确性.与文献中的常规方法[9−11]相比,其优势具体体现在以下四方面.
1)数值原子轨道基的使用极大地减小了计算量(计算量级为10Na),可以快速、准确地模拟周期性体系或者包含很大真空层的超胞.
2)在每一电子和离子步中,电子密度都将自洽演化并通过平均场理论计算出激发态的实时轨迹,可以给出光激励下的电子和原子核超快动力学的微观图像.
3)原子核附近的电子状态可以通过原子轨道的线性组合得到有效的处理,因此可以实现对内层电子激发的理论模拟,研究较高能量范围飞秒和亚飞秒时间尺度的电子动力学.
4)受限于计算效率,传统的rt-TDDFT大多只能在动量空间的单点上进行计算,无法实现体系的动量分辨.近期我们发展了动量分辨的rt-TDDFT算法,可以用很小的单胞计算固体和表面,从而使计算成本降低了几个数量级.此外,我们还发现体系激发状态在动量空间上的不同区域存在明显差异,表明该方法有利于揭示深入细致的微观机制.
因此,该方法能够在广泛的量子系统中精确、有效地处理各类超快动力学过程,成为解释并预测新奇量子现象的强大工具.本文简单介绍TDAP软件的核心算法,并结合一些实例,介绍软件的主要特色和部分已经实现的功能.
2 计算方法
rt-TDDFT算法的主要框架继承于较早版本的TDAP[13],基于开源软件包SIESTA[14,15].图1描述了在给定离子步时对激发态模拟的流程图.与早期版本略有不同的是,本文方法能够进行动量分辨的时间演化,从而能够适用于有限尺寸低维体系和周期性体系.下面均以这种一般性的动量分辨rt-TDDFT算法为例.
2.1 哈密顿量及交迭矩阵
在周期性边界条件下,晶格矢量用Rs(s=1,2,3,···)表示,单胞中的原子i的位置为bi. 每个原子都有一套数值原子轨道{ξiα}与之对应,其中原子态的轨道和角量子数均用α表示,用多重径向基函数ζ展开[14].为了简化方程形式,本文使用原子单位~=me=e=1.同时,除非特别注明,只有显式依赖于时间t的算符才以f(t)的形式标记.
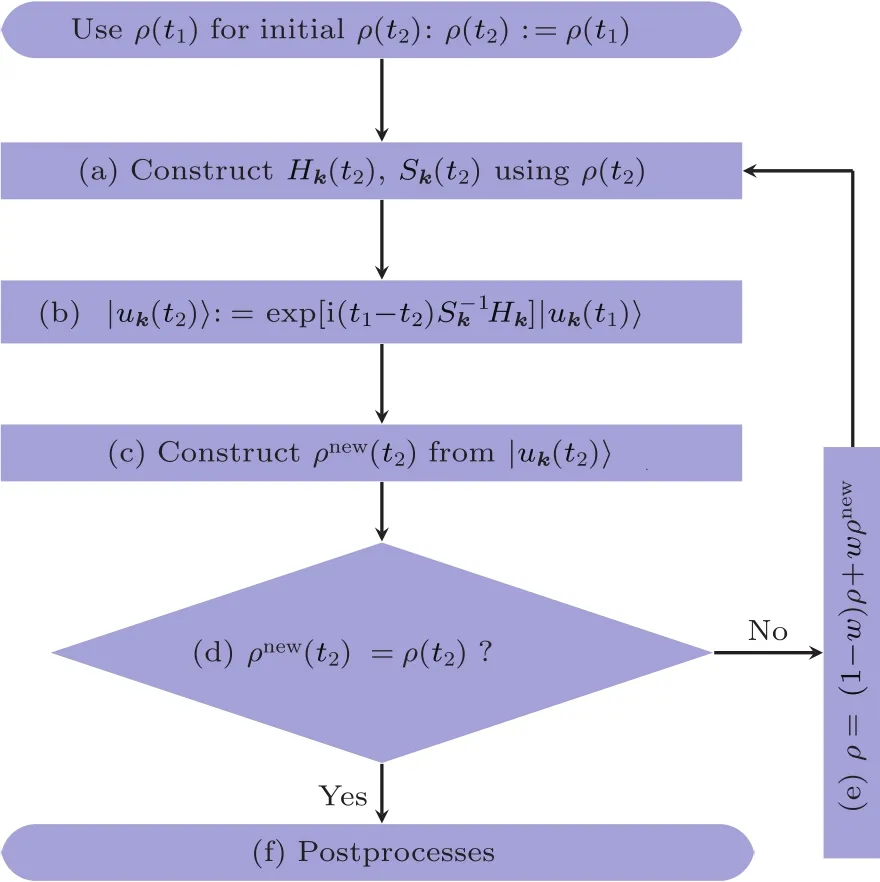
图1 动量分辨的TDDFT算法流程图Fig.1.Flowchart of k-resolved TDDFT algorithm.
在每个k点的交迭矩阵Sk及哈密顿量Hk用原子轨道基表示为
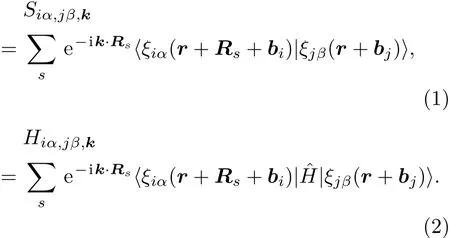
哈密顿算符为
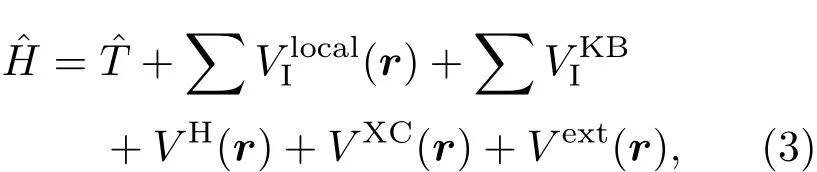
其中为动能算符;及分别是原子I赝势的局域及非局域部分,VH,VXC及Vext分别是Hartree、交换关联及外部电场的势能.目前,我们主要采用绝热局域密度近似或者绝热广义梯度近似作为交换关联泛函.关于的详细计算方法已有文献提及[15],在此不再赘述.
为了模拟光与各种材料之间的相互作用,时间依赖的电场E(t)以两种形式体现在哈密顿量中:长度或者速度规范.在长度规范下,电场E(t)由标量势Vext引入:
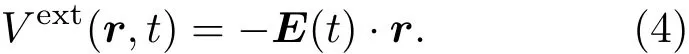
为了防止哈密顿量的平移对称性被电场E(t)破坏,可以在空间方向µ∈x,y,z上施加一个锯齿状的电场:
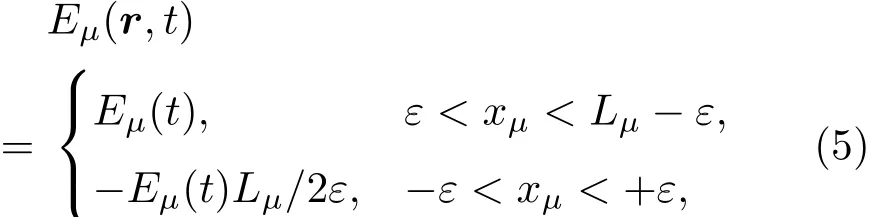
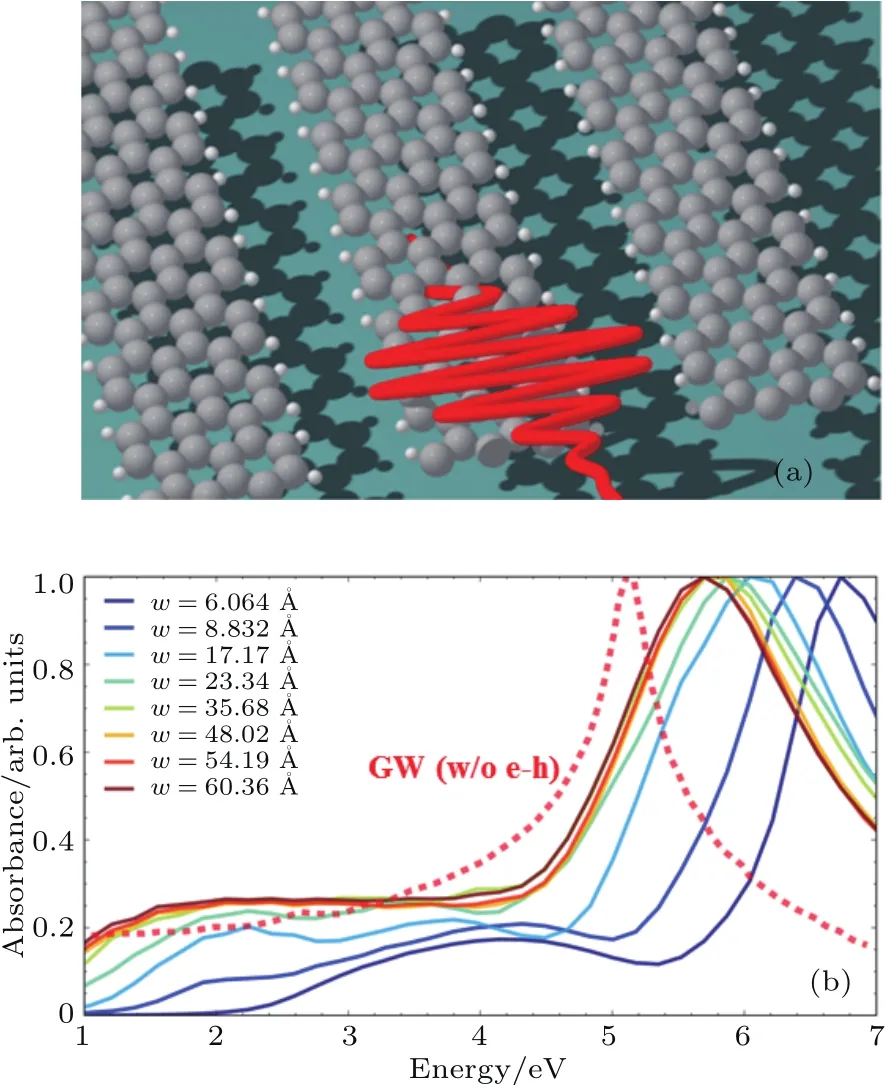
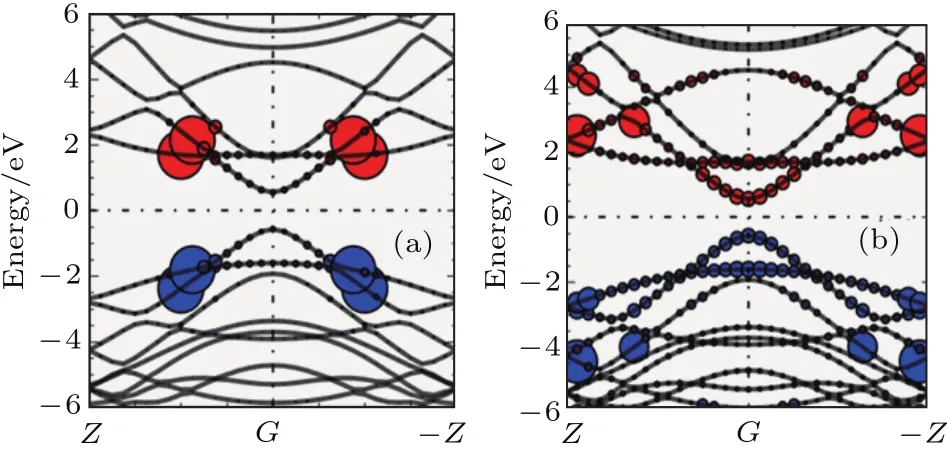
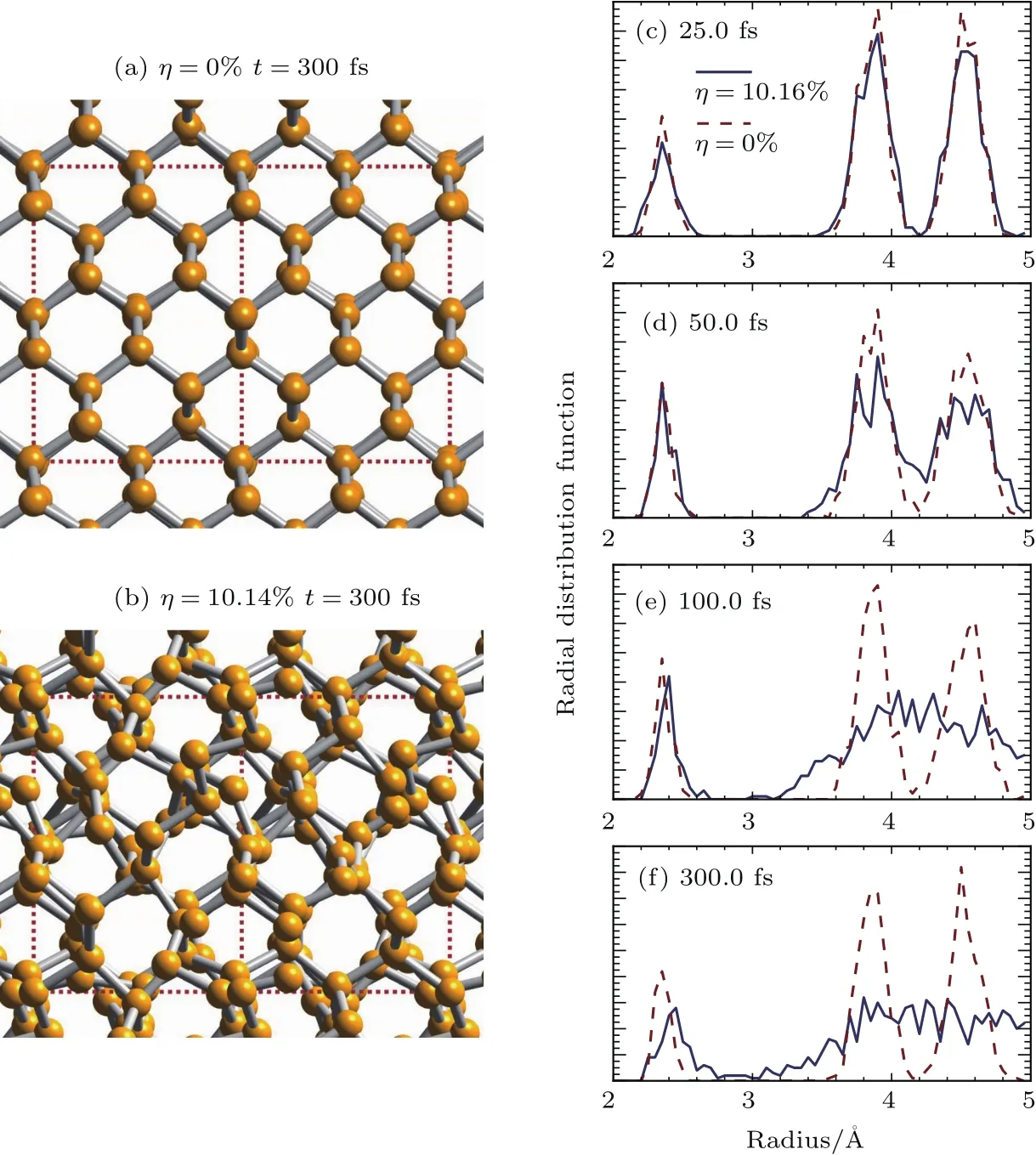
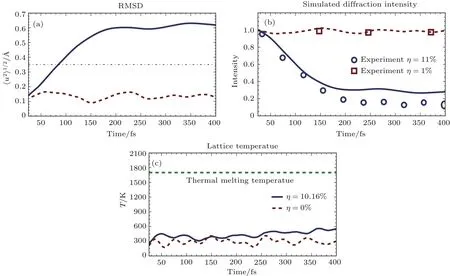
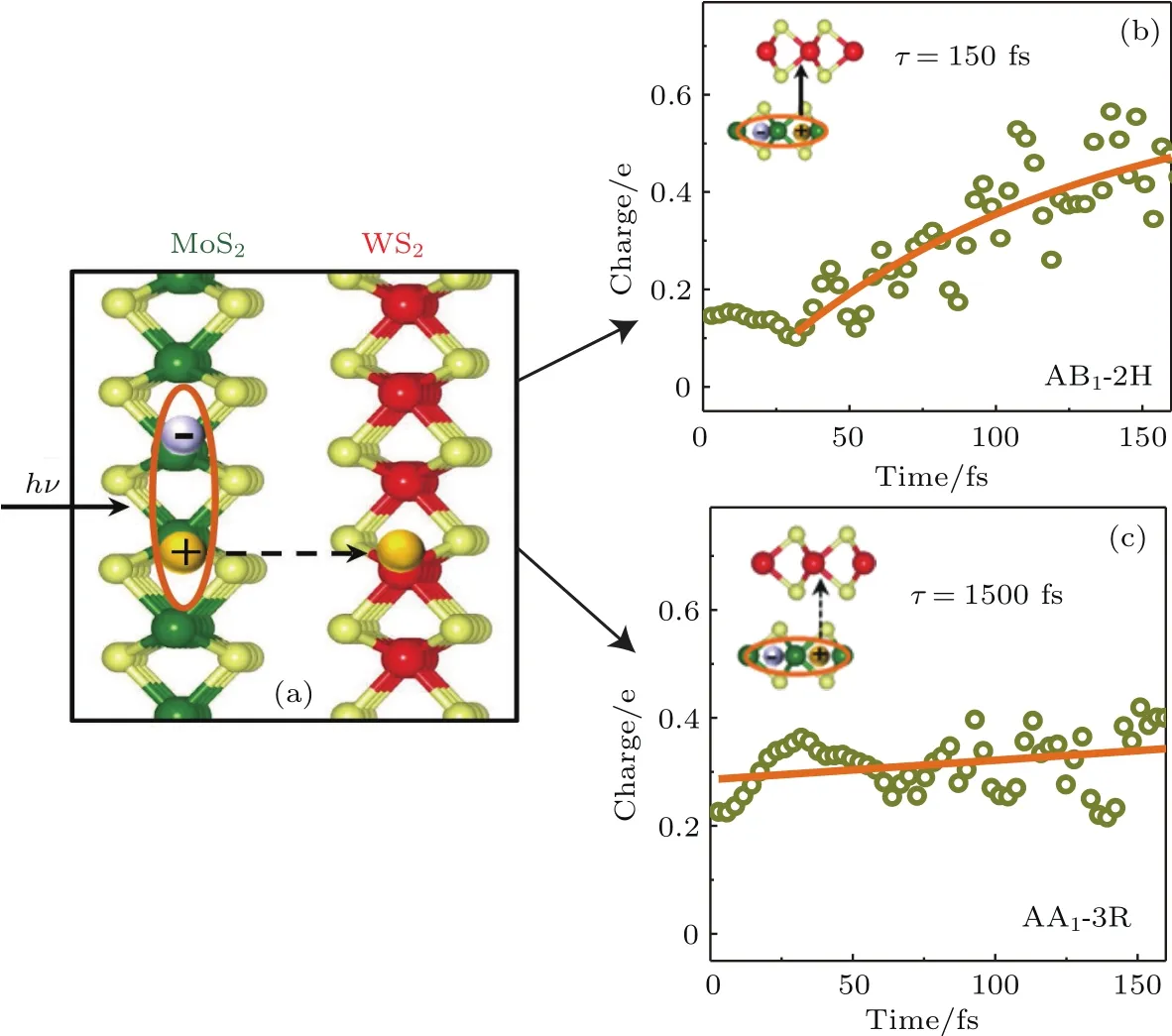
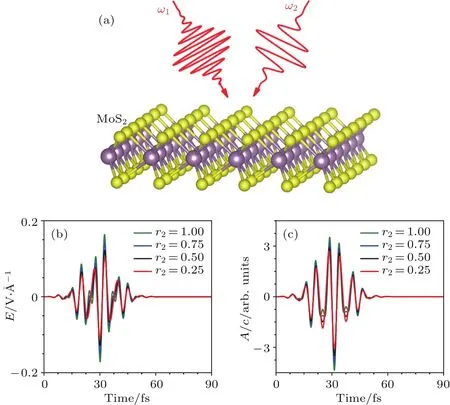
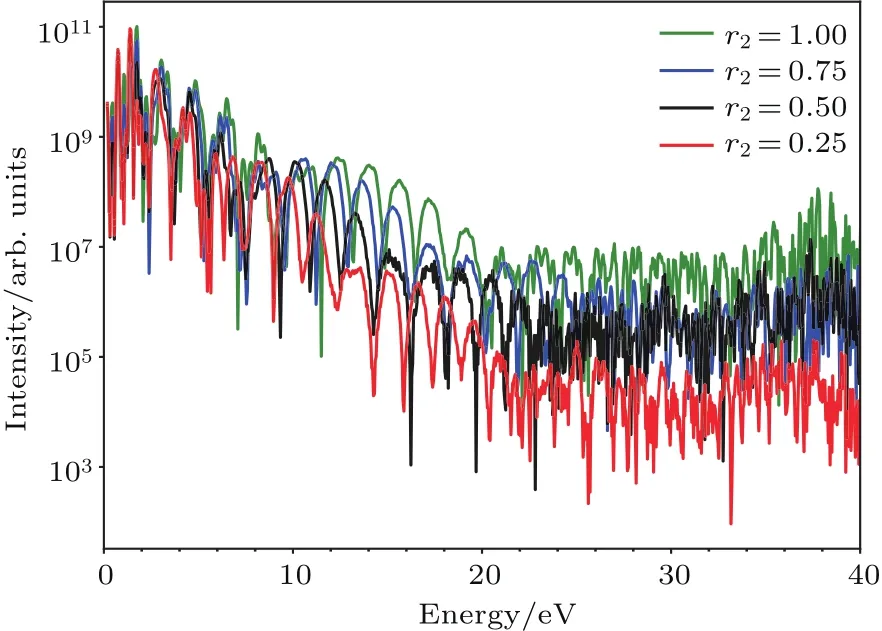
其中Lµ是沿着µ方向的原胞长度,并且ε→0.因此需要保证ρ(xµ)在−ε 为了弥补上述不足,通过度规变换 可以将TDKS方程用速度规范表达,用于对无限大周期性体系的动力学描述.此时哈密顿量为 此外,E(t)的波形在这两种情形下均可任意调节.例如,可采用高斯波包形式: 其中f为激光频率,t0为峰值时间,ϕ为附加相位. 有了随时间演化的哈密顿量以及交迭矩阵后,利用TDKS方程就可以由上一个时间步的状态数据得到新时刻的波函数unk(r,t): 其中unk(r,t)=ψnk(r,t)exp(−ik ·r)是布洛赫波函数ψnk(r,t)的空间周期性部分,而t′≈(t1+t2)/2,∆t=t2−t1为时间的步长.通常,∆t是个小量(<0.05 fs),离子位置bi在t1到t2的时间段内几乎不变,所以对Sk(t)能够保证Sk(t′)=Sk(t2)这一假设的合理性.然而,由于电子态迅速演化,Hk(t)在不同时刻有很大差异,此时有两个选择: 目前已有文献指出,哈密顿算符在0.2—0.5 fs几乎线性变化,所以当∆t<0.05 fs时后者给出的结果更加准确[17,18].另外,对于TDKS方程,当采用ν表示时,尽管unk(r)(t2)并不显式地依赖其他的TDKS轨道un′k′(r)(t1)(n′̸=n或者k′̸=k),但是由于Hk由电荷密度决定,为所有被占据轨道的加权求和,所以能带间的散射已经被考虑[1]. 数值实现上,可用一阶Crank-Nicholson形式展开方程(10)中的演化算符 在技术层面上,方程(13)的计算速度可以通过两方面加速:首先,采用ScaLAPACK做并行的矩阵求逆以及矩阵乘法;其次,为了缩短计算时间,的数值只在离子位置bi改变时才进行更新,所以,当离子位置固定时,只在第一个离子步计算 电荷密度矩阵ρiα,jβ(t2)可通过方程(10)计算出的unk(r,t2)得到: 其中,qn,k为第n个能带在动量空间k点的占据数;cn,jβ,k(t2)为数值原子轨道基中各个基矢对unk(r,t2)的贡献, 在波函数演化过程中,采用电子密度自洽演化能够显著地提高计算结果的稳定性[19].以电荷密度差作收敛判定标准为例,当 且η≈10−4时可认为达到收敛标准.若未达到,则需要使用密度矩阵的线性组合来生成下一个循环的输入量ρnext: 其中ρ,ρnew分别为输入、输出的密度矩阵;w为混合比例,通常为0.1—0.5.值得指出的是,TDAP与SIESTA软件开发的所有收敛测试标准都兼容. 有效数据的提取将在自洽过程结束后进行,其中包括对总能量、Hellmann-Feynman力等物理量的计算.本文只介绍部分独特的分析方法. 首先,本文方法可以计算不同能态之间跃迁的概率[20]: 其中vnk为绝热基矢, 绝热态nk上的电子占据数qnk由TDKS轨道上的投影得到: 其中nk,occ为在k点的占据态. 其次,对于不同种类的模拟体系采用不同的响应函数,代表系统对外界刺激(比如光场)的响应.对于有限大小的结构,在有真空层的方向计算与时间相关的电偶极矩: 其中ρ(r)为电荷密度.然而,对于具有周期性的体系,偶极矩的定义失效,此时,则采用含时的微观电流作为响应函数: 目前,我们已将基于原子轨道基的rt-TDDFT方法应用到一些典型系统的超快动力学研究中.研究重点在于低维体系中电子-光子、声子-光子及电子-声子的相互作用.下面给出应用TDAP计算的几个具体例子,包括石墨烯纳米带的光吸收性质、超快激光诱导的硅晶体非热熔化、MoS2/WS2界面间的电荷传输以及双色光调制下的高次谐波产生. 首先介绍如何利用rt-TDDFT方法计算椅式石墨烯纳米带(armchair graphene nanoribbons,AGNRs)的光吸收,并根据动量分辨的优势监控其激发细节.对于AGNRs[21,22],由于纳米带平面存在真空层,所以可以采用光场的长度规范.同时,沿着µ∈(x,y,z)方向的光吸收强度可定义为介电函数的虚部: 其中αµ,υ代表在频域偶极矩Pµ(ω)对电场Eυ(ω)的响应, 在rt-TDDFT的计算中,首先向体系施加电场来获得偶极矩在时域上的变化,然后进行傅里叶变换: 其中Eυ(t)可选作单位阶跃函数, 如图2(a)所示,Eυ(t)沿着纳米带的宽度方向.图2(b)显示了不同宽度纳米带从红外到紫外光波段(1—7 eV)的吸收光谱.我们观察到在不同的能量范围内存在两种不同的激发模式,其峰值分别位于可见光波段(1—4 eV)以及紫外波段(6—7 eV).随着纳米带宽度的增加,这两种模式都有明显的红移和收敛趋势,这与已有的实验事实高度一致[23,24].对于紫外波段的激发模式,单调的红移(随着宽度从6.064 Å增加到60.36 Å,峰位由6.7 eV红移至5.6 eV)可以外推到单层石墨烯的π—π跃迁(红色虚线)[25,26],这说明了该演变对应于一维纳米带向二维石墨烯能带结构的转变.这与使用GW准粒子近似但是不考虑激子效应计算石墨烯光吸收谱得到的结果相符合[25],表明rt-TDDFT方法具有很高的精确性. 另一方面,对于可见光区域的激发模式,当纳米带的宽度达到无穷大时,尖锐的吸收峰将扩展为一个平滑等高的吸收区域,对应于单层石墨烯2.3%的吸收平台区[27].同时,以上现象在电场强度变化时仍保持不变,说明了两种激发模式的普遍性. 为了得到更细致的动力学信息,借助TDAP对动量的分辨能力,图3展示了宽度为6.064 Å的纳米带的不同吸收模式在激发过程中,能带上不同k点的电子占据情况.对于可见光模式,电子激发主要集中在个别独立的k点上.相比之下,高能吸收模式中,电子的激发趋向于集体性质的k点分布.因此,可见光吸收模式有着个体激发的特征,而高能模式则包含更多集体激发的特点. 图2 (a)光场沿着宽度方向激发椅型纳米带;(b)不同宽度纳米带的光吸收谱Fig.2.(a)Schematic showing AGNRs under an external electric fi eld polarized long the ribbon width;(b)optical absorption spectra of AGNRs with di ff erent sizes. 图3 两种激发模式下的电子占据 (a)可见光区;(b)紫外光区Fig.3.Snapshot of electron population distribution of two modes:(a)Visible light(3.9 eV);(b)ultraviolet(6.73 eV)excitation. 激光激发能够产生诸多超快现象以及新的物质凝聚态[28].在皮秒时间尺度下,光激励导致的熔化过程已经在很多半导体[29−31]和二维材料[32,33]中被观察到.然而,超快熔化的原子机制仍然处于争议之中.由此,我们模拟了在实验条件下硅的激光熔化[33,34].基于含时密度泛函以及分子动力学相结合的模拟结果表明,在没有激光时,由于热扰动,晶格温度在300 K左右振荡.我们用激发到导带上电子的百分比η来代表激光强度,光场持续时间为25 fs.图4(a)和图4(b)显示了在η=10.16%以及η=0%两种情况下由激光诱导的结构差异.图4(b)展现的结构畸变显然由光诱导并显示出熔化的特征.图4(c)—(f)为在光场结束后,Si—Si键的径向分布函数在t=25,50,100,300 fs不同时刻的分布.可以看出第一个峰值逐渐向右移动,这意味着最近邻距离的增加;同时所有的峰均变得更宽,表征晶体结构正在被破坏. 为了进行更定量的描述,我们采用Lindemann熔化标准(Lindemann criterion):当硅原子平均平方位移的根ment,RMSD)大于临界点Rc=0.35 Å时则认为熔化发生[35].从图5(a)可以看出:在没有激光(η=0%)时,RMSD的极大值仅为Rc的一半;然而,当激光的强度为η=10.16%时,RMSD在100 fs内就到达Rc并且持续增大,显示出很明显的熔化行为.另一方面,RMSD与衍射强度I(t)通过Debye-Waller方程相关联: 其中,Q为被探测晶体平面的倒易晶格矢量;⟨u2(t)⟩为平均平方位移,即为RMSD的平方.在图5(b)中,我们模拟(220)晶面的Iη=10.16%(t)以及Iη=0%(t),同时将已有实验数据列出作为比较.可以看出,模拟结果和实验数据的特征基本一致:Iη∼11%(t)的数值在硅熔化后降低至0.2,然而Iη∼0%(t)只在0.95附近振荡.由于在整个模拟过程中晶格的温度远远小于热熔化温度(图5(c)),说明该过程为激光诱导的非热熔化.非热熔化可以归因于电子从成键态到反键态之间的转移,导致随后熔化势垒的降低. 图4 硅的非热熔化[34] (a),(b)不同光场强度下原子结构的变化;(c)—(f)径向分布函数的时间演化Fig.4.Nonthermal melting of silicon[34]:(a),(b)The atomic structures during laser melting;(c)–(f)time evolution of radial distrubution function under two laser intensity η. 图5 (a)RMSD随时间的变化;(b)硅(220)晶面衍射强度随时间的变化;(c)晶体的温度变化[34]Fig.5.(a)RMSD as a function of time;(b)simulated and experimental electron di ff raction intensity of(220)re fl ection as a function of time;(c)time evolution of ionic temperature[34]. 激光诱导的层间超快的电荷传输在决定电荷分离的速度和效率方面起着非常重要的作用,为光电器件的应用提供了新的平台[36,37].如图6(a)所示,以MoS2/WS2双层体系为例,展示该方法如何被用来监控这种范德瓦耳斯异质结构的电子动力学[38].通过选择光子的能量恰好等于MoS2的带隙大小,电子将从特定的态上激发并在MoS2留下空穴,随后空穴会进一步传递到WS2.通过同时求解TDKS方程以及离子的运动,可以得到界面间电子的动力学演化.结果表明,通过施加扭转、平移、改变层间距等结构调制方法,能够非常有效地调节电荷传输的动力学过程.在图6(b)和图6(c)中,AB1-2H与AA1-3R均是MoS2/WS2双层体系的稳定结构,且层间距离相同(6.3 Å),但两层间旋转180◦[39].统计受光场激发后WS2轨道空穴(电子)密度的时间演化χ,并用指数函数χ=a+b×exp(−t/τ)拟合[40],其中τ为电荷传输的寿命.如图6(b)和图6(c)所示,τAB1及τAA1分别在100 fs及1000 fs的时间尺度.进一步的分析表明,层间的电荷转移只与某些特定层间态之间的耦合相关,在该情形下,为布里渊区的K点的|−2⟩及|−1⟩态.用偶极跃迁矩阵元M=⟨−2|ˆZ|−1⟩来衡量这两个态之间的耦合强度,其中ˆZ为沿着垂直MX2平面方向的位置算符.发现MAB1≫MAA1且1/τ指数依赖于M.根据以上发现就能够从微观机制上理解两种结构间电荷传输动力学过程的差异,并且为控制电荷传输的量子动力学过程提供了新的途径,从而促进二维异质结构在新奇光电器件中的应用. 图6 MoS2/WS2双层之间的超快电荷传输[38] (a)MoS2/WS2双层结构的侧视图;(b),(c)两种MoS2/WS2结构下电荷传输过程,内插图为对应的原子结构Fig.6.Ultrafast charge transfer in MoS2/WS2bilayer[38]:(a)Side view of MoS2/WS2bilayer;(b),(c)hole transfer dynamics for MoS2/WS2in two stacking modes,the insets show the schematic atomic structure. 强激光辐照下,固体能够产生高度非线性的电子和光学行为.在非线性光学中,一个最基本和重要的方面即是在凝聚态系统中的高次谐波产生(high harmonic generation,HHG)[41−44]. 通过HHG可以重构电子运动的微观图像并产生更高能的超短脉冲.然而,HHG的应用却一直受限于其较低的产率,所以如何提高脉冲的强度已成为当今超快科学领域中非常重要的课题. 如图7(a),采用双色光来调控单层MoS2中电子的动力学过程.光与MoS2之间的相互作用通过求解速度规范下的TDKS方程(方程(6))得到.双色激光场表示为高斯波包包络的正弦函数: 图7 (a)模拟体系示意图;(b)不同r2下的电场波形和(c)矢势波形Fig.7.(a)Schematic showing high harmonic generation in monolayer MoS2under two-color fi elds;(b)the electric fi eld and(c)the vector potential of four representive laser pulses with various r2. 其中,Ei,φi及ωi(i=1,2)为两束光的电场峰值大小、相位及频率;两者之间的相对强度比用r2表示,r2=E2/E1.在我们的模拟中,激光的极化方向沿着MoS2的zigzag方向并且设定E1=0.07 V/Å,ω1=1/3Egap,ω2=1/2Egap(Eg=1.94 eV),φi=0,脉冲峰值时间t0=30 fs,半高宽σ=8.5 fs.在图7(b)和图7(c)给出了不同r2下的激光波形. 图8 不同r2下的高次谐波产生谱Fig.8.HHG spectra under two-color fi elds with di ff erent relative intensity ratio r2between two laser pulses. 图8所示的HHG谱可以通过方程(7)及(22)计算出的电流J(t)做傅里叶变换得到:可以很明显地看出,通过简单的控制第二束光的强度,在适当的双色场中,高阶谐波的强度在E>10 eV的能量范围内可以提高10—100倍.与此对比,输入光的总强度在峰值处的变化仅为40%(0.0525 V/Å).同时,平台区的截断能也得到了扩展,提供了生成孤立的阿秒脉冲的可能[45,46].以上现象归因于第二束激光脉冲的参与可以获得更大的矢势. 本文介绍了一种自主发展的基于数值原子轨道基的rt-TDDFT模拟方法,用于对凝聚物质激发态的动力学过程进行大规模、精确的模拟.电磁场的长度和速度规范的有效使用,保证了该方法在处理固体、界面以及二维材料中各类超快过程时的灵活性和可靠性.作为实例,把该方法应用于几个典型的体系,如石墨烯纳米带的光吸收性质、单晶硅的非热熔化、MoS2/WS2界面间的电荷传输、双色光调制的高次谐波产生等,它们均代表着超快光学领域中的研究热点.通过模拟可以得到与实验事实和其他高精度计算方法高度一致的结果,并且能从微观电子结构的角度解释其工作机理.我们希望该方法可以扩展到更广阔的研究领域,成为物理学家、化学家和材料学家研究工作中的有效工具. [1]Runge E,Gross E K 1984 Phys.Rev.Lett.52 997 [2]Ullrich C A 2011 Time-Dependent Density-Functional Theory:Concepts And Applications(Oxford:Oxford University Press) [3]Sato S,Yabana K,Shinohara Y,Otobe T,Lee K M,Bertsch G 2015 Phys.Rev.B 92 205413 [4]Takimoto Y,Vila F,Rehr J 2007 J.Chem.Phys.127 154114 [5]Sánchez-Portal D,Hernandez E 2002 Phys.Rev.B 66 235415 [6]Lopata K,Govind N 2011 J.Chem.Theory Comput.7 1344 [7]Yabana K,Sugiyama T,Shinohara Y,Otobe T,Bertsch G 2012 Phys.Rev.B 85 045134 [8]Castro A,Werschnik J,Gross E K 2012 Phys.Rev.Lett.109 153603 [9]Yost D C,Yao Y,Kanai Y 2017 Phys.Rev.B 96 115134 [10]Andrade X,Strubbe D,de Giovannini U,Larsen A H,Oliveira M J,Alberdi-Rodriguez J,Varas A,Theophilou I,Helbig N,Verstraete M J 2015 Phys.Chem.Chem.Phys.17 31371 [11]Sato S A,Yabana K 2014 J.Adv.Simulat.Sci.Eng.1 98 [12]Meng S,Kaxiras E 2008 J.Chem.Phys.129 054110 [13]Ma W,Zhang J,Yan L,Jiao Y,Gao Y,Meng S 2016 Comp.Mater.Sci.112 478 [14]Soler J M,Artacho E,Gale J D,García A,Junquera J,Ordejón P,Sánchez-Portal D 2002 J.Phys.Condens.Matter 14 2745 [15]Ordejón P,Artacho E,Soler J M 1996 Phys.Rev.B 53 R10441 [16]Yabana K,Nakatsukasa T,Iwata J I,Bertsch G 2006 Phys.Status Solidi(b)243 1121 [17]Wang Z,Li S S,Wang L W 2015 Phys.Rev.Lett.114 063004 [18]Ren J,Vukmirović N,Wang L W 2013 Phys.Rev.B 87 205117 [19]Ren J,Kaxiras E,Meng S 2010 Mol.Phys.108 1829 [20]Rohringer N,Peter S,Burgdörfer J 2006 Phys.Rev.A 74 042512 [21]Son Y W,Cohen M L,Louie S G 2006 Phys.Rev.Lett.97 216803 [22]Yang L,Park C H,Son Y W,Cohen M L,Louie S G 2007 Phys.Rev.Lett.99 186801 [23]Yan H,Li X,Chandra B,Tulevski G,Wu Y,Freitag M,Zhu W,Avouris P,Xia F 2012 Nat.Nanotech.7 330 [24]Ju L,Geng B,Horng J,Girit C,Martin M,Hao Z,Bechtel H A,Liang X,Zettl A,Shen Y R 2011 Nat.Nanotech.6 630 [25]Yang L,Deslippe J,Park C H,Cohen M L,Louie S G 2009 Phys.Rev.Lett.103 186802 [26]Trevisanutto P E,Holzmann M,Côté M,Olevano V 2010 Phys.Rev.B 81 121405 [27]Gomez C V,Pisarra M,Gravina M,Pitarke J M,Sindona A 2016 Phys.Rev.Lett.117 116801 [28]Ostrikov K K,Beg F,Ng A 2016 Rev.Mod.Phys.88 011001 [29]Shank C,Yen R,Hirlimann C 1983 Phys.Rev.Lett.50 454 [30]Harb M,Ernstorfer R,Hebeisen C T,Sciaini G,Peng W,Dartigalongue T,Eriksson M A,Lagally M G,Kruglik S G,Miller R D 2008 Phys.Rev.Lett.100 155504 [31]Sokolowski-Tinten K,Blome C,Dietrich C,Tarasevitch A,von Hoegen M H,von der Linde D,Cavalleri A,Squier J,Kammler M 2001 Phys.Rev.Lett.87 225701 [32]Porer M,Leierseder U,Ménard J M,Dachraoui H,Mouchliadis L,Perakis I,Heinzmann U,Demsar J,Rossnagel K,Huber R 2014 Nat.Mater.13 857 [33]Hellmann S,Beye M,Sohrt C,Rohwer T,Sorgenfrei F,Redlin H,Kalläne M,Marczynski-Bühlow M,Hennies F,Bauer M 2010 Phys.Rev.Lett.105 187401 [34]Lian C,Zhang S,Meng S 2016 Phys.Rev.B 94 184310[35]Zijlstra E S,Kalitsov A,Zier T,Garcia M E 2013 Phys.Rev.X 3 011005 [36]Falke S M,Rozzi C A,Brida D,Maiuri M,Amato M,Sommer E,de Sio A,Rubio A,Cerullo G,Molinari E 2014 Science 344 1001 [37]Rozzi C A,Falke S M,Spallanzani N,Rubio A,Molinari E,Brida D,Maiuri M,Cerullo G,Schramm H,Christoffers J 2013 Nat.Commun.4 1602 [38]Zhang J,Hong H,Lian C,Ma W,Xu X,Zhou X,Fu H,Liu K,Meng S 2017 Adv.Sci.4 1700086 [39]van der Zande A M,Kunstmann J,Chernikov A,Chenet D A,You Y,Zhang X,Huang P Y,Berkelbach T C,Wang L,Zhang F 2014 Nano Lett.14 3869 [40]Long R,Prezhdo O V 2016 Nano Lett.16 1996 [41]Ndabashimiye G,Ghimire S,Wu M,Browne D A,Schafer K J,Gaarde M B,Reis D A 2016 Nature 534 520 [42]Luu T T,Garg M,Kruchinin S Y,Moulet A,Hassan M T,Goulielmakis E 2015 Nature 521 498 [43]Vampa G,Hammond T J,Thire N,Schmidt B E,Legare F,McDonald C R,Brabec T,Corkum P B 2015 Nature 522 462 [44]Liu H,Li Y,You Y S,Ghimire S,Heinz T F,Reis D A 2016 Nat.Phys.13 262 [45]Li J B,Zhang X,Yue S J,Wu H M,Hu B T,Du H C 2017 Opt.Express 25 18603 [46]Shiner A D,Trallero-Herrero C,Kajumba N,Bandulet H C,Comtois D,Legare F,Giguere M,Kie ff er J C,Corkum P B,Villeneuve D M 2009 Phys.Rev.Lett.103 073902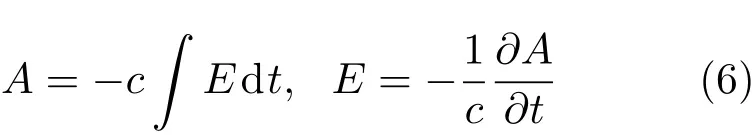
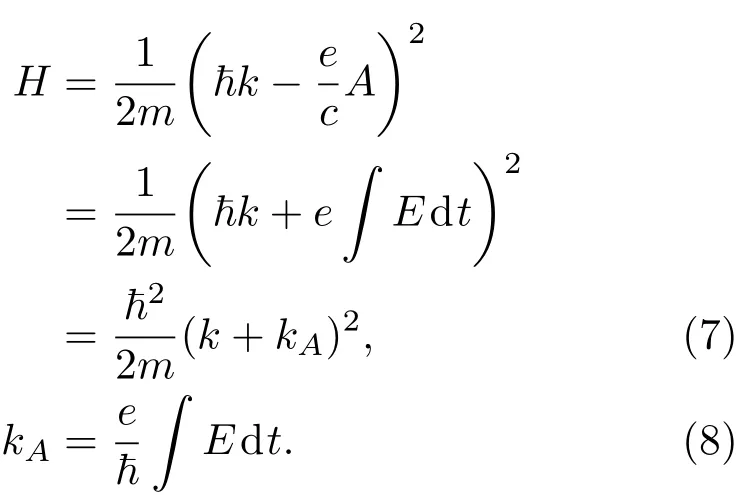
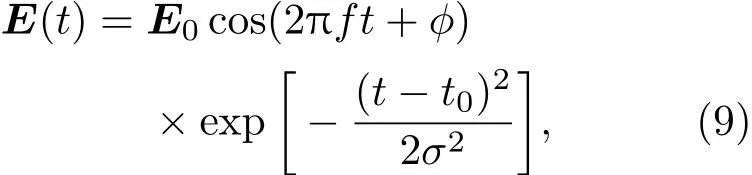
2.2 电子态演化
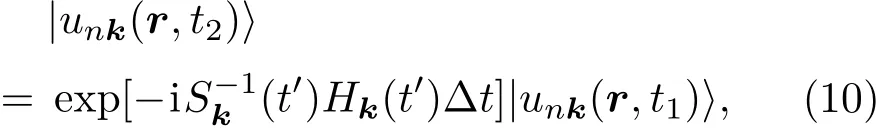
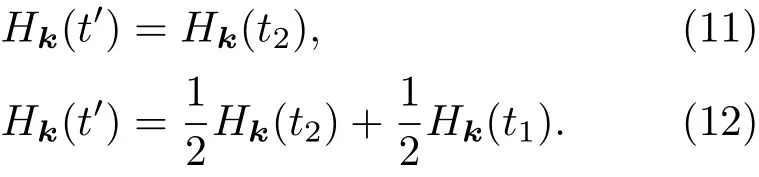
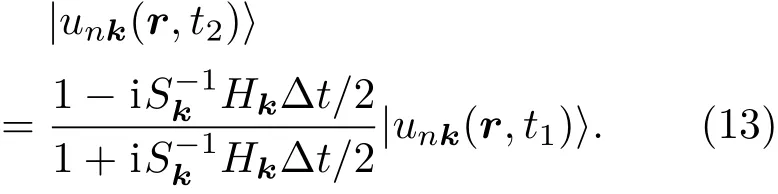
2.3 电荷密度以及自洽计算
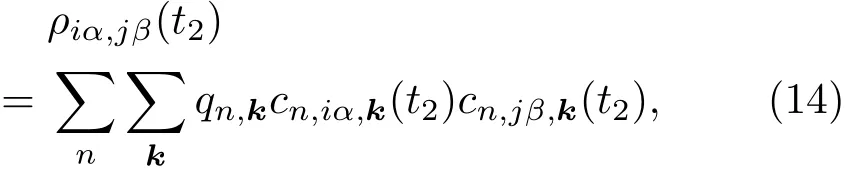
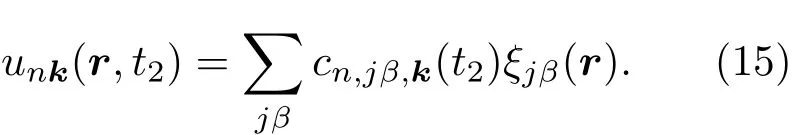
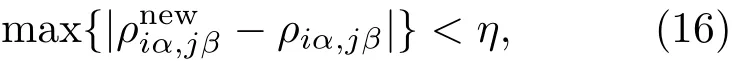
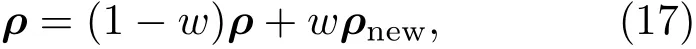
2.4 数据处理
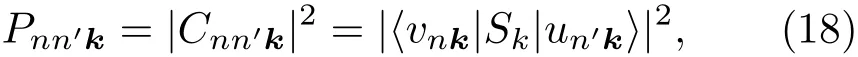

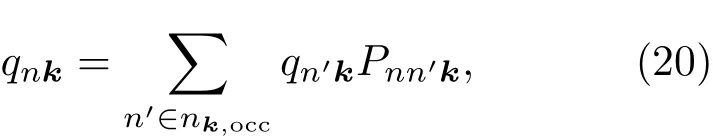
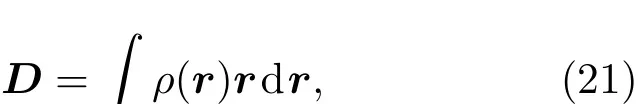

3 计算实例
3.1 石墨烯纳米带的光吸收谱及电子动力学模拟
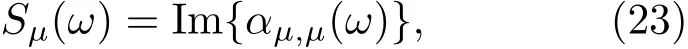
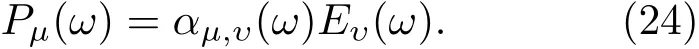
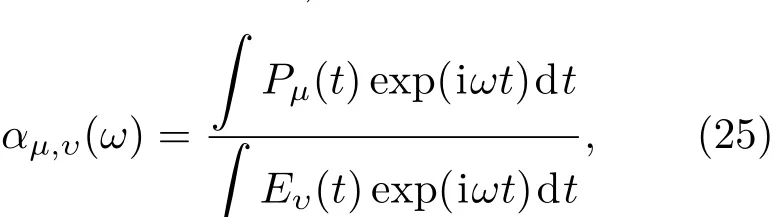
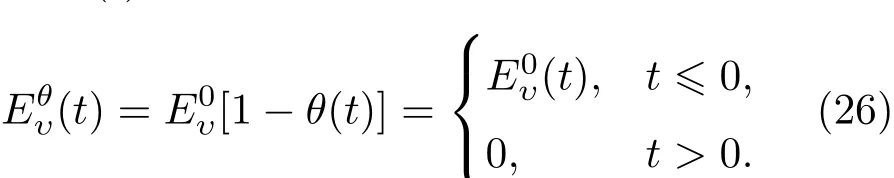
3.2 超快激光诱导的单晶硅的非热熔化
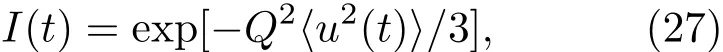
3.3MoS2/WS2界面间的电荷传输
3.4 双色光调制的高次谐波产生
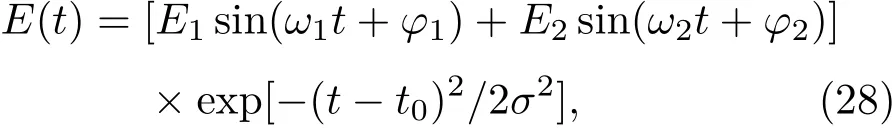

4 结 论
