模糊线性分式规划的标准型及其最优值区间

吴　丽， 孙玉华

(北京科技大学 数理学院， 北京 100083)

0　引　言

分式规划在实际问题中有着广泛的应用. 例如， 在经济管理领域中， 若分母表示总生产成本， 分子表示总产值， 则目标函数表示产出率； 若分母表示投资额， 分子表示总收益， 则目标函数表示盈利率. 此外， 分式规划在运输问题、 经济效应问题、 排队论、 聚簇分析等问题中也有着广泛的应用. 而且， 在处理双目标规划时， 分式规划也是一种很好的选择， 它不仅可以将双目标问题转化为比例目标问题， 避免了给各个目标直接或者间接地设置权重， 还为平衡两个目标之间的关系提供了更多有价值的关键信息[1]. 目前， 分式规划方法已经在很多领域得到了较多的应用. 例如： Lara等[2]开发了一个应用于农业系统的多目标线性分式规划(MLFP)模型， 其目标是获得单位用水量下系统利润的最大值. Gomez等[3]将分式规划模型应用于古巴森林采伐作业调度问题的研究中， 来平衡该地区木材年龄层的分布问题. 此外， Zhu等[4-5]在2013年和2014年分别讨论了动态随机分式规划(DSFP)模型和区间参数分式规划(IMIF-EP)模型， 并应用于电力系统规划中.

在线性分式规划的求解问题上， 何文汉等[6]提出了一个直接处理一般形式线性分式规划的算法， 并且证明了算法在有限步后终止于原问题的最优解. 时凌[7]讨论了线性分式规划问题的最优性条件， 证明了它的局部最优解一定是整体最优解， 并且局部最优解一定在约束条件的基本可行解处达到. 谢政[8]介绍了线性分式规划的原始单纯形法， 说明了LFP性质， 并引进了Gilmore-Gomory方法和Charnes-Cooper方法. Rafael Caballero和Monica Hernandez[9]用一种简单可行的检验方法验证了线性分式目标规划问题是否有解， 如果存在解， 怎样通过线性规划问题找到最优解. 薛声家等[10]使用多面集的表示定理， 导出了线性分式规划最优解集的结构， 给出了确定全部最优解的计算步骤. 郭晓芳等[11]针对一类上层为线性规划、 下层为线性分式规划的区间系数双层规划问题， 提出了一种基于系数取值区间搜索的遗传算法. 王国栋等[12]针对一类非光滑多目标分式优化问题， 建立了此类优化问题有效解的必要条件和充分条件， 并研究了其Mond-Weir对偶模型. 汪春峰等[13]针对极大极小分式规划问题， 给出了一个新的线性松弛化技巧， 构造了一种新的分支定界算法.

目前对线性分式规划的研究一般仅限于确定型问题， 然而在实际问题中， 由于数据的非精确性与模糊性， 很多信息往往无法精确得到， 对于这类更具有柔性与现实意义的不确定型线性分式规划的研究则更有意义. 本文在模糊数的最佳逼近区间的基础上， 提出了一种新的求解模糊线性分式规划的方法. 首先， 提出了模糊数的最好最优解、 最差最优解及其最优值区间的定义， 将模糊线性分式规划问题转化为基于模糊数最佳逼近区间的区间线性分式规划问题. 其次， 将区间线性分式规划问题的最优值求解转化为求解4个确定型的线性分式规划问题， 进而利用Gilmore-Gomory算法求解. 最后给出该方法在实际中的数值算例， 验证了该方法的有效性与可行性.

1　预备知识

定义1[14]设R为实数域， 称闭区间[aL,aR]为区间数， 其中aL,aR∈R,aL≤aR, 用A来表示A=[aL,aR],aL,aR分别称为A的左端点和右端点, 当aL=aR=a时， 区间数A就退化为实数a.

定义2[14]对于两个区间数A=[aL,aR],B=[bL,bR],k为确定数， 定义

A+B=[aL+bL,aR+bR],

A-B=[aL-bR,aR-bL],

定义3[15]对区间数A=[aL,aR],B=[bL,bR], 记len(A)=aR-aL,len(B)=bR-bL, 则称

P(A≤B)=

为A≤B的可能度； 考虑约束条件Ax≤B， 则称λ=P(Ax≤B) 为约束条件下的满意水平.

定义4[16]设U为论域， 则U上的一个模糊集合A由U上的一个实值函数

μA∶U→[0,1],

u|μA(u)

来表示. 对于u∈U， 函数值μA(u)称为u对于A的隶属度， 而μA称为A的隶属函数. 当论域U为无限集时，U上的模糊集合A可表示为

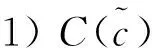
考虑如下形式的线性分式规划(LFP):

s.t.Ax=b,x≥0,

其中，A为m×n矩阵,p,q,x∈En,b∈E1. 不失一般性， 可设rank(A)=m≤n. 记(LFP)的可行集为S.

给出Gilmore-Gomory算法[18]：

Step 1给定一个初始可行基B， 写出相应的单纯形表；

Step 2计算r(xN)， 如果r(xN)≥0， 则关于B的基本可行解x*为最优解， 停止计算； 否则， 转Step 3；

Step 3确定进基变量. 令

-rk=max{-rj|rj<0,j∈N}

则xk以为进基变量；

Step 4确定离基变量. 由

确定xr为离基变量；

2　模糊线性分式规划模型的建立

本文定义如下一种标准类型的模糊线性分式规划(FLFP)：

xj≥0,j=1,2,…,n.

对于求解模糊规划问题， 一般做法是利用模糊隶属函数的α-截集， 将模糊数转化为区间数， 从而求解区间规划. 然而， 由于α取值不同， 结果往往也不同， 为此需要考虑最优的解. 基于文献[17]中模糊数最佳逼近区间的定义， 首先把模糊线性分式规划转化为如下区间线性分式规划(ILFP)：

xj≥0,j=1,2,…,n,

假设(ILFP)目标函数的分母大于零， 否则可将目标函数的分子分母同时乘以-1.

由引理1， 在约束条件满意度为λi的情况下， (ILFP)问题可以转化为

xj≥0,j=1,2,…,n.

3　模糊线性分式规划问题的求解

i=1,2,…,m,xj≥0,j=1,2,…,n.

下面给出模糊线性分式规划(FLFP)的最优值区间定义以及最好最优值、 最差最优值的求解．

定义10设(FLFP)问题的最优值集合为S， 称ZL=min{Z|Z∈S}为(FLFP)问题的最好最优值； 称ZR=max{Z|Z∈S}为(FLFP)问题的最差最优值； 称[ZL,ZR]为(FLFP)问题的最优值区间.

定理1(FLFP)的最好最优值在(ILFP)的目标函数分子取左端点， 分母取左端点或右端点处达到.

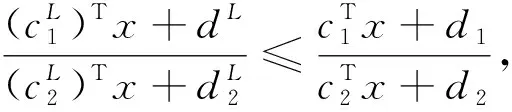
由定理1， (FLFP)的最好最优值可以转化为求解如下两个确定型的线性分式规划

j=1,2,…,n,(1)

j=1,2,…,n.(2)

将式(1)和式(2)中的不等式约束通过增加松弛变量使其变为等式， 再利用修改的凸单纯形法分别进行求解， 取较小的最优值作为(FLFP)的最好最优值.

定理2(FLFP)的最差最优值在(ILFP)的目标函数分子取右端点， 分母取左端点或右端点处达到.

证明与定理1类似,此处略.

由定理2， (FLFP)的最差最优值可以转化为求解如下两个确定型的线性分式规划

j=1,2,…,n.(3)

j=1,2,…,n.(4)

将式(3)和式(4)中的不等式约束通过增加松弛变量使其变为等式， 再利用修改的凸单纯形法分别进行求解， 取较大的最优值作为(FLFP)的最差最优值.

4　数值算例

下面通过数值算例检验模型和算法的有效性与可行性.

如下是一个实际问题中的简化模型

xi≥0,i=1,2,3,(5)

其中， 模糊数

s.t. [5,6.25]x1+[2.2,3.2]x2+

[2.6,3.1]x3<0.8[9.4,12.4],

[8.6,10.6]x1+[2.3,3.3]x2+[4.5,9.5]x3≤

0.7[9.7,10.7],xi≥0,i=1,2,3.(6)

1) 根据定理1， 求解式(5)的最好最优值可以转化为求解如下两个确定型线性分式规划

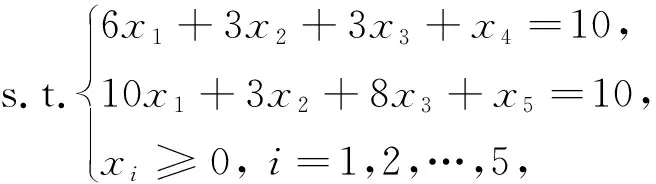
用Gilmore-Gomory算法[18]解式(7)， 得最优单纯形表如表 1 所示.

表 1　最优单纯形表Tab.1　The best simplex table

2) 根据定理2， 求解式(5)的最差最优值可以转化为求解如下两个确定型线性分式规划

5　结　论

线性分式规划问题在现实生活中具有广泛的应用， 特别是在经济问题， 运输问题以及排队问题上， 而具有柔性的模糊线性分式规划则具有更为广泛的现实意义. 本文定义了模糊线性分式规划的标准型及其最优值区间， 并给出了一种新的求解模糊线性分式规划的方法. 然而对于模糊线性分式规划的其他求解方法以及模糊非线性分式规划的求解问题， 还有待进一步探讨.