基于部件更新的海上风电场备件数量优化

符 杨, 杨 凡, 王泽宁

(1.上海电力学院, 上海 200090; 2.美国洛杉矶钻石吧高中, 美国 洛杉矶 90001)

近年来,我国海上风电事业发展迅速,根据国家能源局《风电发展“十三五”规划》,到2020年,全国海上风电开工规模要达到10 GW,累计并网容量力求达到5 GW以上。海上风电场装机规模越来越大,需要维护的机组也越来越多。海上风电机组的维护成本一般至少是陆上机组的2倍,运维成本占整个风电项目成本的18%～23%[1],因此海上风电机组的维护越来越受到关注。

备件管理是海上风电维护的重要部分。若备件数量过少,当部件发生故障需要更换时,备件库中没有可用备件,需要等待备件补足才能进行更换,将会造成长时间停机;若备件数量过多,则会造成资源浪费。因此,合理配置风电场备件数量对于海上风电场的正常运行至关重要。

目前,关于备件数量的研究方法有数据预测法、模型分析法、序贯分析法3类[2]。数据预测法是以备件数量历史数据为依据,建立备件需求量的预测模型,文献[3- 4]主要采用该方法进行研究。文献[3]以有限可修复备件的维护次数为约束条件,综合考虑了装备数量和工作时间,运用数理统计方法,建立了有限可修复备件消耗规律预测模型。文献[4]针对舰载机随舰出航过程中,舰载机间断型备件的需求预测的特殊性,提出了一种基于时间聚合的备件预测方法。模型分析法是根据装备的配置,利用建模工具建立系统模型,优化求解所需的备件数量。文献[5]针对部件寿命分布难确定、备件数量难预测的问题,建立了一种基于正态近似的指数型备件需求预测模型。文献[6]同时考虑费用和备件保障度两个因素,在分析鱼雷备件保障度要求的基础上,建立了一次性备件需求量优化数学模型。文献[7]研究了寿命服从指数分布的备件在故障后采取更换策略时,装备的任务可用度与备件携行量的关系。序贯分析法根据装备的任务要求和可靠性、保障性参数,利用系统工程、随机过程等理论对装备进行维护工作分析,确定维护方案,从而确定备件的种类和数量。文献[8]对农机工作特点与预测方法进行了分析,利用BP神经网络算法建立备件需求量的预测模型。以上文献主要考虑了部件事后更换对备件数量的优化。文献[9-10]主要从部件预防性更换的角度优化备件数量。文献[9]采用遗传算法与粒子群优化算法对预防性维护策略与备件库存管理进行联合优化,并以电动起重机维护为例,说明这两种智能算法运算时间短,优化效果较好。文献[10]结合状态维护与备件库存管理决策,通过启发式算法确定备件最优库存以及状态维护阈值。

海上风电领域的备件数量优化与上述文献有所不同。海上风机部件的事后更换必须在部件发生故障后进行,此时需要考虑人员、船只以及天气可及性的问题,易造成长时间停机,风机可用率降低。因此,海上风电部件更换除了事后更换,还需结合维护策略,考虑预防性更换,以减少停机时间。另外海上风机离岸较远,环境恶劣,部件劣化过程复杂,状态监测技术不够完善[8],有些部件如齿轮箱等还需要维护人员现场检测,因此需要建立不定期检测维护策略。

针对上述问题,本文建立了基于部件更新的海上风电备件数量优化模型。首先,基于时间延迟理论,建立不定期检测的海上风机维护策略,优化维护策略以确定风机检测间隔及部件更新周期(即部件故障率)。其次,考虑部件循环周期,构建基于部件更新的马尔科夫过程,并以部件可用率为目标函数确定备件数量。

1 基于时间延迟维护理论的部件更新策略

1.1 基于时间延迟的维护策略

时间延迟理论由CHRISTER于1973年提出,是一种综合考虑设备故障损失、运行风险和成本的维护模型。在时间延迟理论中,设备从投入运行到产生潜在故障的时间间隔为u,u为一随机变量,密度函数为g(u),经过一段时间s,s亦为一随机变量,密度函数为h(s),设备将发生功能故障[11]。理论示意图如图1所示。

图1 时间延迟理论示意

若在空白区域进行检测,将不能检测出潜在故障或潜在故障已演变成功能性故障[12];若检测周期不合理,会导致部件状态无法准确预测,从而影响机组可用率。确定合理的检修周期就是确保延迟时间能被充分利用,使得运行维护部门能在斜线时间区域内对部件进行检修,从而实施预防性更换。

在本文采取的维护策略中,不定期对设备进行检测,检测时间序列为{I1,I2,I3,…,Ik},用Uk=Ik-Ik-1表示第k次检测与上一次检测的时间间隔。令I0=0,检测时间与部件更换时间忽略不计。每次的部件检测费用为CD,检测出潜在故障并对部件进行预防性更换的费用为Cp,检测间隔期对发生功能性故障部件进行修复性更换的费用为Cc,单位时间的停机损失费用为Cd。其中,若检测出潜在故障,则对部件进行预防性更换,每次预防性更换时间为dp;若在检测间隔期内发生功能性故障,则对部件进行故障更换,故障更换时间为dc;若在第k次检测时间点Ik没有检测出潜在故障,则不实施维修,并按Uk+1=αkU1(0<α<1)确定下一次检测时间。

对部件进行更换后,部件更新有3种情况。

(1) 从零时刻开始运行,在第一次检测时刻I1前发生功能性故障,此时运行时间为u+s,更新周期为u+s+dc,更换成本为CD+Cc+Cddc。

(2)I1时刻检测出潜在故障,此时运行时间为I1,更新周期为I1+dp,更换成本为CD+Cp+Cddp;

(3) 在I1时刻未检测出潜在故障,此时又包含两种情形:在Ik(k≥2)时刻第一次检测出潜在故障,且在(I1,Ik)内没有发生功能性故障,则更新周期为Ik+dp,更新成本为kCD+Cp+Cddp;在前k次检查时没有检测出潜在故障,且在Ik+1时刻前发生了功能性故障,则更新周期为Ik+1+dp,更新成本为kCD+Cc+Cddc。

综合以上所有情况,部件的更新周期T的期望为

(1)

在更换周期内成本C的期望为

(2)

根据Ross更新理论有

(3)

以单位时间的运行成本最小为目标,建立以下优化模型。

(4)

通过优化算法,求得部件更新周期优化参数(I1,a),获得检测序列。

1.2 部件更新周期分析

为了对部件更新周期进行具体分析,本文对任一连续性随机事件ζ作如下离散化处理:若某一随机事件的概率高于某概率阈值Ω,则认为其在实际中已经发生。

在t时刻,可求得部件在该时刻发生功能性故障的概率pb和发生潜在故障的概率pu。其中,部件在t时刻发生功能性故障的概率为1-R(t),R(t)的表达式为

(5)

部件在t时刻发生潜在故障的概率表达式为

(6)

因此,若在某检测间隔内,满足pb≥Ω或pu≥Ω,则认为其已发生功能性故障或潜在故障,需进行更换,由此可确定部件的更新周期。

2 海上风电场备件数量优化策略

2.1 基于部件更新策略的马尔科夫构建

海上风电场的重要部件价格昂贵,从风机上更换下来后会通过维护部门回到备件仓库中继续循环利用。本文考虑备件的循环利用,建立马尔科夫过程。结合上文内容,用优化所得的更新周期(倒数)代替部件故障率,对备件循环利用过程构建马尔科夫链。基于备件更新策略的备件循环利用过程如图2所示。

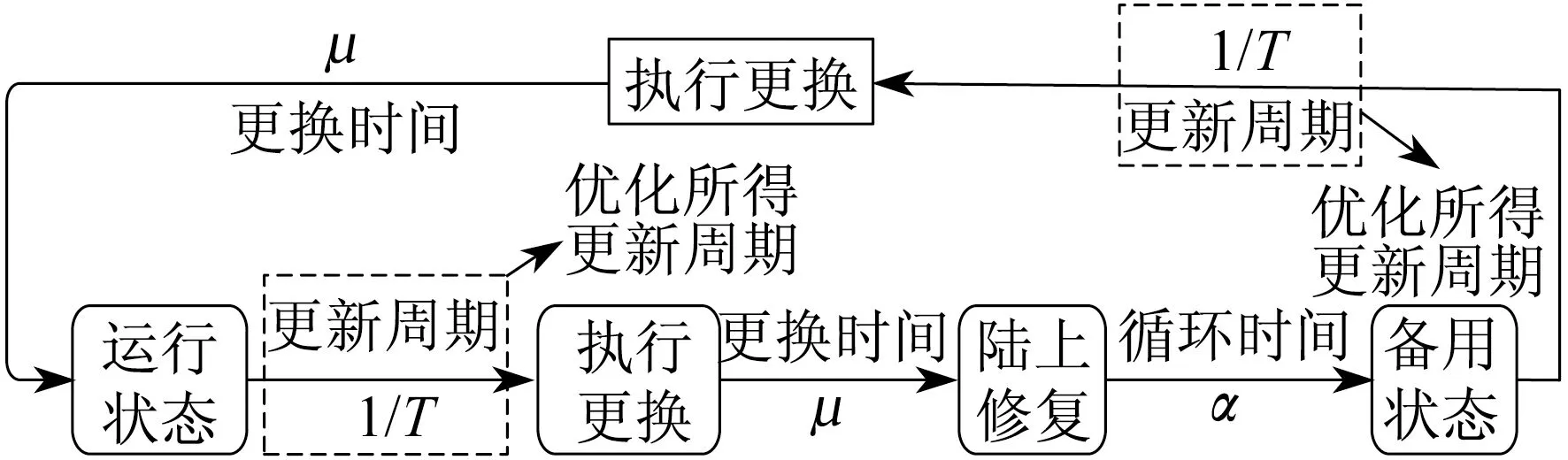
图2 基于备件更新优化的备件循环利用过程

在多数情况下,更换备件所需时间比备件更新周期和备件平均循环时间少得多。为了简化分析,本文假设更换是瞬时完成的。

假设风电场有m台机组,则整个风电场运行的某部件数量也为m。若风电场备件库中该备件初始数量为n,用 (i1,i2,i3)表示该风电场备件循环利用的马尔科夫过程中的状态。其中,i1表示风电场正常运行的某部件数量;i2表示备件库中可用的该部件备件数量;i3表示处在循环过程的部件数量。假设在一定年限内,风电场该部件不发生报废也不新添备件,则i1+i2+i3的值保持不变,为m+n。对系统所有的状态用j=i3来编码,则共有m+n+1种状态。

令初始状态为(m,n,0),描述上述各个状态间转移的马尔科夫过程如图3所示。

图3 备件循环利用的马尔科夫过程

马尔科夫方程为

(7)

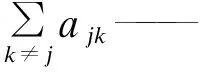
根据式(7)和图3,马尔科夫方程组包含以下两个部分。

对于前n+1种状态,有

(8)

式中:p(n),p′(n)——系统处在状态n的概率及其一阶导数;

λ——故障率,为部件的平均故障间隔时间的倒数;

α——循环速率,为平均循环时间倒数。

从以下状态开始,部件将出现备件短缺,且有

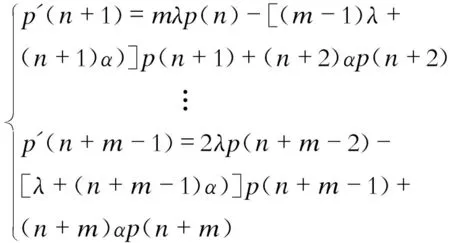
(9)

综上,本文构建的马尔科夫过程考虑了备件的更新与循环,能够表征备件运行过程中的各个状态。

2.2 备件数量优化

传统备件优化过程以备件保障率或备件短缺概率为优化目标,备件保障率和备件短缺概率是表征备件充足性大小的值,只要风电场备件库处于可用备件数为零的状态,就会贡献备件短缺概率。然而,在实际运行中,若发生备件短缺时,没有备件需要更新,备件短缺就不会对运行可用率产生影响,这是传统备件优化中以备件保障率为优化目标的不足之处。鉴于此,本文采用稳态可用率作为目标函数进行优化。

令U(L)表示风电场有L个备件短缺情况下系统的不可用率,则不可用率期望为

(10)

因假设更换是瞬时完成的,即当没有出现备件短缺时,可用率为1,则有

(11)

对于风电场的部件i,当运行数目为m,备件数目为n时,其稳态可用率Ai(n)为

(12)

由式(12)可以看出,稳态可用率与风电场实际运行状态有关,通过稳态可用率对部件的备件数量进行优化,可以使得备件数量更合理。

3 算例分析

以100台机组构成的海上风电场为例,假设风电场的机组为同一型号,以整个风电场部件可用率为约束,对齿轮箱初始备件数量进行优化。g(u)和h(s)分布组合为指数分布和威布尔分布。其中,指数分布参数为0.020 5,威布尔分布尺度参数为0.001 6,形状参数为1.56。齿轮箱单价为300万元,齿轮箱循环时间为32天,运维参数参考文献[13-15]。

3.1 维护策略优化及部件更新周期获取

根据前文,优化得到齿轮箱的检测结果如表1所示。其中,最佳检修序列为(I1,α)=(141,0.26)。

表1 齿轮箱检测优化结果

当Ω=0.9时,齿轮箱更新周期优化结果如下:I1时刻,(pb,pu)=(0.49,0.82);I2时刻,(pb,pu)=(0.89,0.92);I3时刻,(pb,pu)=(0.93,0.94)。可以看出,在I2时刻,pu>0.9,此时齿轮箱发生潜在故障,对其进行预防性更换,由此可得到齿轮箱更新周期为177.66天。

3.2 备件数量优化结果对比

分别以备件保障率和部件可用率大于0.95为优化目标,在满足相同概率约束条件下,两种目标函数优化出的齿轮箱数量分别为23和11,以齿轮箱单台价格300万计,备件费用分别为6 900万元和3 300万元。采用可用率为目标函数,5年内能节约齿轮箱备件费用(不含库存费用)3 600万元,减少52%。两者优化结果差异较大的原因在于,以备件保障率为优化目标时,没有考虑备件的备用状态与运行部件更新状态之间的动态关系,会造成备件的过度配置。由此可见,以部件可用率为优化目标,能够大大节约备件管理成本。

3.3 成本变化分析

通过离散化分析,由Ω值可以确定部件预防性更换周期。当Ω不同时,齿轮箱备件成本也会有所不同,如表2所示。

表2 不同Ω值时的备件成本变化

当Ω<0.91时,备件成本随着Ω的增大而降低;当Ω>0.91时,备件成本随着Ω的增大有所增加。由表2可知,备件成本并不是随着Ω值的增大而单调下降,因此合理确定部件预防性更换周期可以减少备件成本。

4 结 论

本文结合部件预防性维护策略,提出了基于部件更新的备件数量优化方案。经过对风电机组齿轮箱的仿真分析,得出以下结论。

(1) 针对海上风电机组的特殊性,考虑备件预防性更换的备件数量优化方案,可有效解决备件数量优化问题,为优化海上备件数量提供了新的思路。

(2) 部件更换周期的优化不仅可减少维护成本,也能减少备件成本。不合理的部件预防性更换周期不仅会造成部件寿命利用不完全,还会导致备件成本的增加。

参考文献：

[1] 傅质馨,袁越.海上风电机组状态监控技术研究现状与展望[J].电力系统自动化,2012,36(21):121-129.

[2] 崔谱龙,叶华平,闫华.多阶段任务系统备件携行量研究方法综述[J].兵器装备工程学报,2018(1):127-135.

[3] 刘慎洋,黄之杰,卢松,等.有限可修复备件消耗规律预测方法[J].装甲兵工程学院学报,2017(5):23-26.

[4] 王梓行,韩维,苏析超.舰载机间断型备件的需求预测方法[J].兵工自动化,2017,36(5):40-43.

[5] 易勇华,傅健,王春枝,等.指数型有寿件备件需求预测模型[J].兵器装备工程学报,2017(11):89-92.

[6] 梁庆卫,宋保维,贾跃.鱼雷一次性备件量模糊优化模型研究[J].兵工学报,2007,28(6):700-703.

[7] 张汝政,魏曙寰,陈砚桥.基于任务可用度模型的指数分布型备件随舰携行量计算模型[J].海军工程大学学报,2011,23(4):70-73.

[8] 孙硕.面向预防性维修的备件需求预测与库存优化方法研究[D].北京:北京理工大学,2015.

[9] SAMAL N K,PRATIHAR D K.Joint optimization of preventive maintenance and spare parts inventory using genetic algorithms and particle swarm optimization algorithm[J].International Journal of System Assurance Engineering & Management,2015,6(3):248-258.

[10] RAUSCH M,LIAO H.Joint production and spare part inventory control strategy driven by condition based maintenance[J].IEEE Transactions on Reliability,2010,59(3):507-516.

[11] CHRISTER A H.Developments in delay time analysis for modeling plant ma intenance[J].Journal of the Operational Research Society,1999,50(11):1120-1137.

[12] CHRISTER A H,LEE C.Refining the delay-time-based PM inspection model with non-negligible system downtime estimates of the expected number of failures[J].International Journal of Production Economics,2000,67(1):77-85.

[13] JESSE A A.Maintenace optimisation for wind turbines[D].Aberdeen:The Robert Gordon University,2008.

[14] POORE R,WALFOLD C.Development of an operations and maintenance cost model to identify cost of energy savings for low winds speed turbines[R].Seattle:Global Energy Concepts,2008.

[15] TIAN Z G,JIN T D,WU B R,et al.Condition based maintenace optimization for wind power generation systems under continuous monitoring[J].Renewable Energy,2011,36(5):1502-1509.