舰艇无线信道建模研究*

朱宁龙，高 鑫

（解放军91404部队，河北 秦皇岛 066001）

0 引 言

随着电子信息技术的不断发展，众多新型的通信、雷达以及电子战设备列装与舰艇之上，在狭窄的频谱范围内，电子设备间相互干扰，影响了设备的正常工作。因此，研究干扰信号的来源和传输信道尤为重要。同时，信号在无线信道内的传播过程较为复杂，通常经过反射、绕射和散射才能到达终端，且传播环境在不停发生变化，导致无线信道具有随机性和时变性，严重影响无线信道特性的分析研究[1]。为了准确研究干扰信号的干扰流程，要正确把握无线信道的特征。因此，无线信道建模对于海军舰艇通信具有重要价值。

目前，国内外的科研工作者已经提出了多种信道模型，大致可归纳为两类：（1）基于统计的无线信道模型，主要包括高斯信道模型、瑞利信道模型和赖斯信道模型等[2]；（2）基于特定环境的模型，典型的是几何模型，其主要方法是射线跟踪技术。目前，在舰艇通信研究中使用最多的是第一种模型。但是，由于无线信道的随机性和时变性，使得统计模型误差较大。因此，可使用马尔科夫链算法对该模型进行优化，进而得到最优信道模型。

1 统计信道模型

1.1 高斯信道模型

高斯信道模型用于描述恒参信道，其假定功率谱密度在整个信道带宽下为常数[3]，且接收信号包络的概率密度函数为：

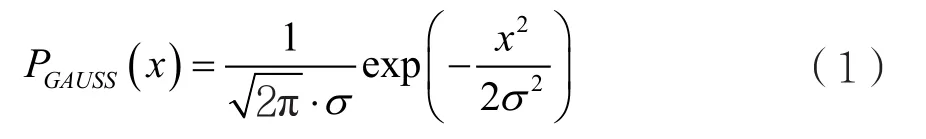
其中x为接收信号包络的幅度，σ2为零均值高斯分布的方差。

由于信号在无线信道内传播过程中不可避免会有信号缺失，通常利用误码率来表征信道的传输特性。误码率是表示信号在一定时间内传输无差错的指标。信号通过调制后，经过高斯信道后的误码率为：

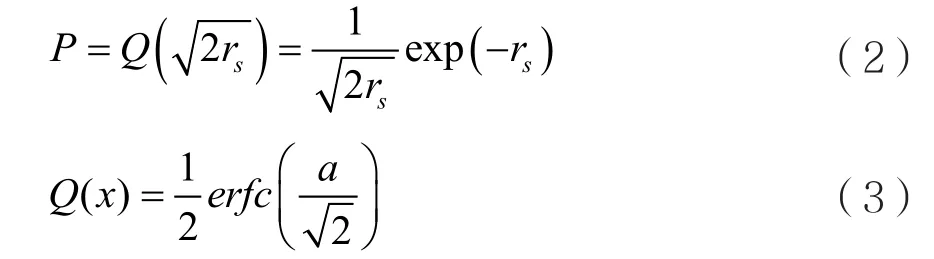
其中rs为信号的信噪比，erfc(·)为互补误差函数。

1.2 瑞利信道模型

瑞利分布是高斯分布的一个扩展，常被用来描述到达接收机的平坦衰落信号包络的统计模型。此模型常用来描述舰艇航行过程中，收发信号时由于散射所产生的无线信道统计特性。它的信号包络概率密度函数(x)为：

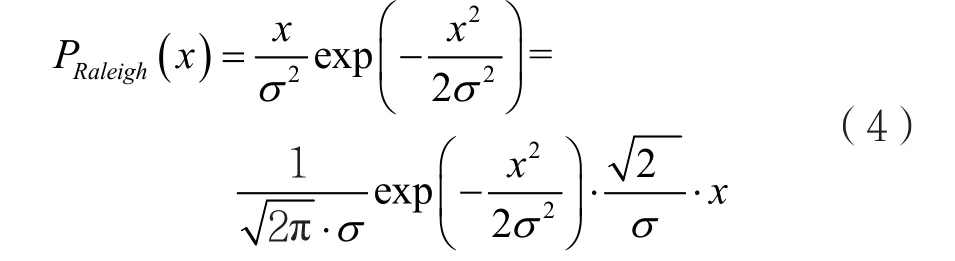
其中，0x≤≤∞。从式（4）可看出，瑞利分布可看作一个零均值高斯分布与一个线性函数的乘积。

依照文献[2]，可求得瑞利信道模型的误码率为：

其中rs为信号的信噪比。

误码率的推导是通过平均功率计算的，而信道模型是包络的统计模型，通过积分计算。于是，式（5）可化解为：

其中rm表示信号通过瑞利信道衰落后的平均信噪比。

1.3 莱斯信道模型

正弦信号通过一个高斯窄带过程后，新信号包络的概率密度函数分布就是莱斯分布[3]。因此，莱斯信道模型可看作一个单独的平面波与众多散射波的叠加。该模型常用来模拟收信机接收主信号和信号散射时信道的情况。莱斯信道统计模型信号包络的概率密度函数(x)为：

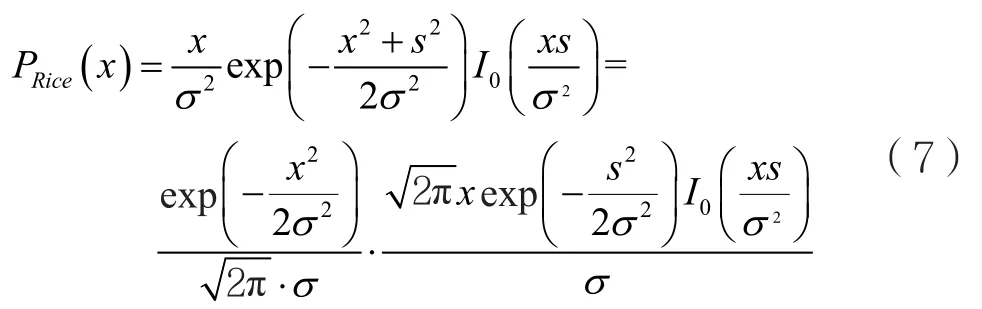
式中，s2为组成莱斯分布的两个高斯分布的方差之和。同样，可求得莱斯分布模型的误码率为：

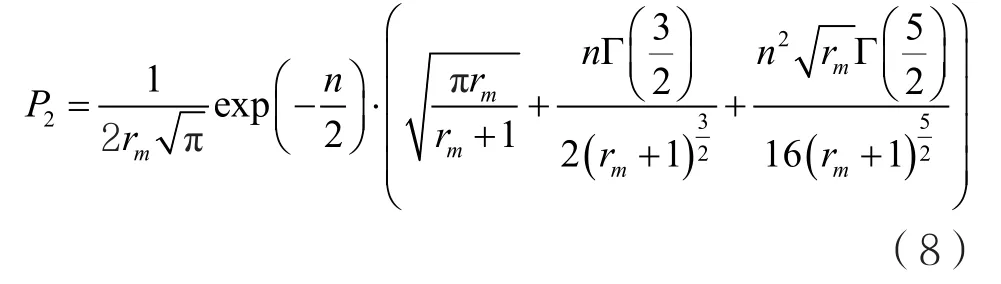
2 马尔科夫链模型建立

因为无线信道具有随机性和时变性，所以上述3种模型并不能准确描述信道的特性，需引入马尔科夫链模型[4]。马尔可夫链在数学中是指具有马尔可夫性质的离散时间随机过程。该过程是指在满足给定信息的条件下，将来事件的状态只与当前的状态有关，与当前以前的历史状态无关。在马尔可夫链的每个时刻，系统依据概率分布进行状态变化。

两态马尔科夫链模型是最基本的马尔科夫链，其状态转移框图如图1、图2所示。定义模型的状态转移矩阵为该矩阵与信号是否进行直线传播和散射传播有关（及与该地的大型障碍物影响对信号传输的影响有关）。该矩阵内的元素代表着两状态工作的概率。定义模型稳态矩阵为其中π1、π2分别是系统稳定在状态1和状态2的概率，满足

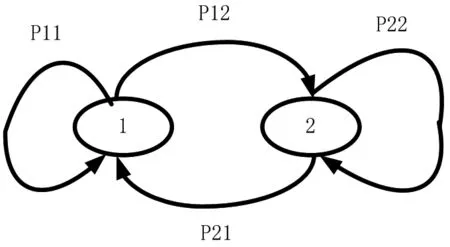
图1 两态马尔科夫链状态转移图

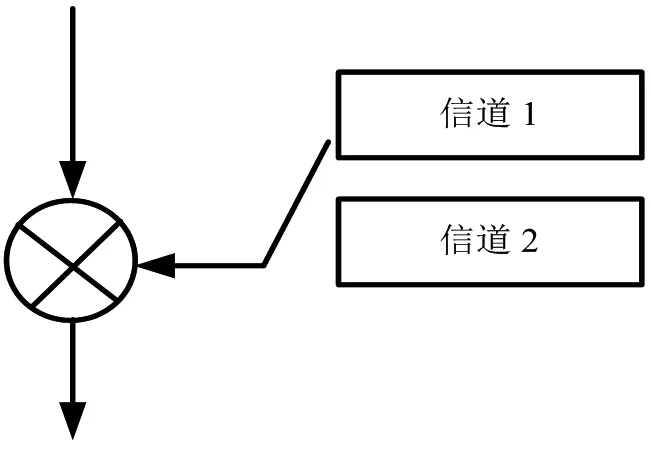
图2 两态马尔科夫信道

根据马尔科夫链的性质，满足：

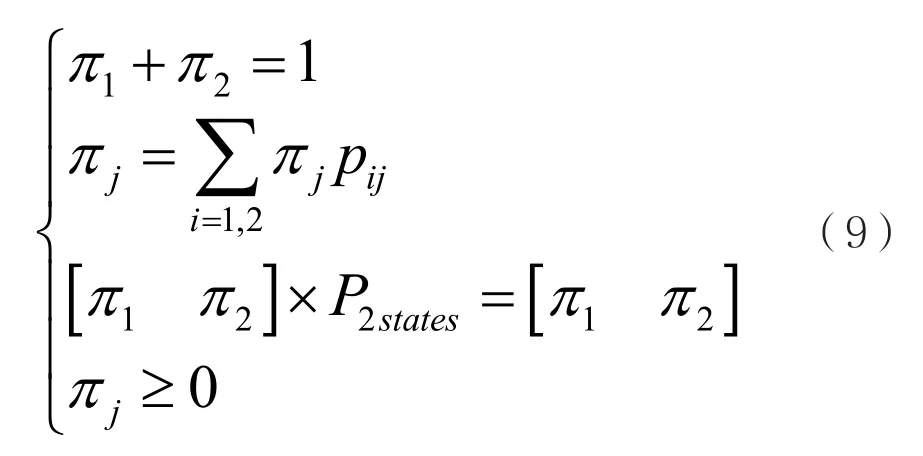
求解方程组（9），即可得到马尔科夫链的平稳分布。

3 两态马尔科夫链模型仿真分析

本次仿真背景设定为典型的QPSK无线通信系统，其码元卷积速率为2/3；仿真的两态马尔科夫链模型如图2所示。该模型是用来模拟仿真无线信道，根据概率转移矩阵进行两种衰落信道的状态转换[3-6]。

由图2可知，马尔科夫链信道在信道1和信道2间相互选择转换。本次仿真假定信道1为莱斯信道衰落，信道2代表瑞利信道衰落。

仿真1：两态马尔科夫链模型状态转移矩阵为模型的稳态此时，信道1一直出现且状态稳定，说明此时信道具有良好的直线传播能力，无线信道可用莱斯信道模型描述。

仿真结果如图3所示，马尔科夫曲线与莱斯曲线精确重合，且随着信噪比的增加，误码率减少。

仿真2：两态马尔科夫链模型状态转移矩阵为模型的稳态此时，信道2一直出现且状态稳定，说明此时收发端存在较大遮挡物，无线信道可用瑞利信道模型描述。

仿真结果如图4所示，马尔科夫曲线与瑞利曲线精确重合，且随着信噪比的增加，误码率减少。综合仿真1和仿真2，验证了马尔科夫链信道的设计原理。

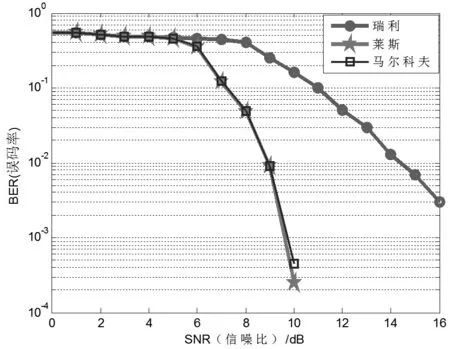
图3 仿真1的误比特率曲线

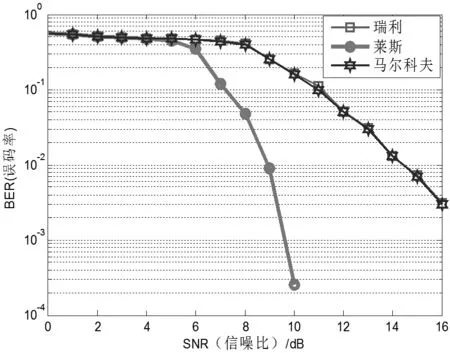
图4 仿真2的误比特率曲线

仿真3：两态马尔科夫链模型状态转移矩阵为模型的稳态由上述两个矩阵可知，信道1出现概率为0.2，信道2出现概率为0.8，说明此时信道大部分能直线传播，但少数受遮挡物影响，无线信道误码率位于瑞利信道模型和莱斯信道模型之间。

仿真结果如图5所示，考虑信道环境的影响，估算马尔科夫链模型状态转移矩阵，就能近似得到该地点的空间信道特性。为了验证仿真对信道模型的模拟效果，计算状态转换次数和稳态出现次数的比例，如表1所示。可以看出，信道转移次数和稳态次数与马尔科夫链设定非常接近，验证了马尔科夫链模型的正确。

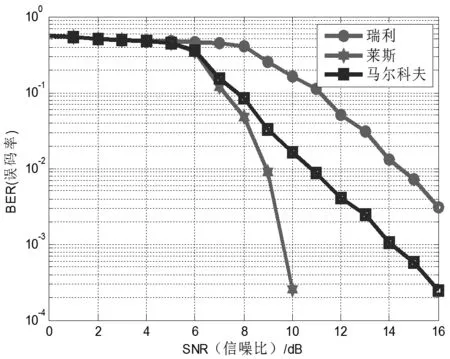
图5 仿真3的误比特率曲线

表1 仿真3状态转移和信道出现比例

4 结 语

本文研究了3种常见的无线信道模型，并使用马尔科夫数学算法，提出了一种近似估计无线信道的简易方法。通过了仿真验证表明，使用两态马尔科夫链模型可以近似描述无线信道。但是，由于信道环境的复杂性，可以将两态马尔科夫链模型扩展到多态马尔科夫链模型，以更加准确地表征无线信道，这也是下一步的研究方向。

[1] 樊昌信.通信原理[M].第6版.北京:国防工业出版社,2006:196-213.FAN Chang-xin.Communication Theory[M].6th ed.Beijing:National Defense Industry Press,2006:196-213.

[2] 邓华.MATLAB通信仿真及应用实例详解[M].北京:人民邮电出版社,2003:1-20.DENG Hua.Matlab Communication Simulation and Application Examples[M].6th ed.Beijing:People’s Post and Telecommunications Press,2003:1-20.

[3] 张丽丽,陈伟.多径衰落信道中QPSK信号传输特性的研究[J].武汉理工大学学报,2007,29(12):43-46.ZHANG Li-li,CHEN Wei.Transmission Characteristics of QPSK Signals in Multipath Fading Channels[J].Journal of Wuhan University of Technology,2007,29(12):43-46.

[4] Kijima,Masaaki.Markov Processes for Stochastic Modeling[M].Cambridge:The University Press.1997.

[5] 张小红,易称福,陈宇环.基于Rayleigh信道模型下的性能分析与仿真[J].江西理工大学学报,2006,27(01):23-26.ZHANG Xiao-hong,YI Cheng-fu,CHEN Yu-huan.Performance Analysis and Simulation Based on Rayleigh Channel Model[J].Journal of Jiangxi University of Science and Technology,2006,27(01):23-26.

[6] 江丽娜,魏琴芳,张祖凡.无线统计信道模型的一种分解表示法[J].重庆邮电大学学报(自然科学版),2013,25(02):252-258.JIANG Li-na,WEI Qin-fang,ZHANG Zu-fan.A Decomposition Representation of the Wireless Statistical Channel Model[J].Journal of Chongqing University of Posts and Telecommunications(National Science Edition),2013,25(02):252-258.