思茅松天然成熟林林分直径结构及环境解释

（西南林业大学 西南地区生物多样性保育国家林业局重点实验室，云南 昆明 650224）

林分结构反映林分内部许多特征因子如直径、树高、树冠等的分布规律，是林分生长、林分经营的理论基础[1-2]。其中，林分直径分布形态对林木的树高、材积、树冠、干性等因子的变化有直接的影响，是最重要、最基本的林分结构[3-4]。再者，从森林经营管理的角度来看，它不但是直接检验经营措施效果的依据，而且直接关系到林分生物量、蓄积量、材种规格以及森林的经济、社会、生态效益[5]。因此，林分直径结构分布的研究具有重要的科研价值和实践意义。

近年来有关林分直径分布规律的研究，多借助于数理统计中的各种概率密度函数，诸如正态分布、对数正态分布、Weibull分布、β分布、Γ分布等分布函数[6-7]。其中，多数研究表明Weibull分布函数在林分直径结构研究中有足够的灵活性、适用性，无论是在研究幼龄林、成熟林、人工林、天然林还是次生林中，都取得了最优的拟合效果[8-13]。

思茅松Pinus kesiya var.langbianensis是松科Pinaceae松属Pinus常绿乔木，适宜生长在云南省部南亚热带与热带地区[14]。由于具有树干端直高大、生长迅速、用途广等优点，已成为云南省荒山造林的先锋树种，同时也是云南省特有的林地类型[15]。其分布面积广、蓄积量大，具有极其重要的经济价值、森林生态服务功能和碳汇效益，在云南省区域林业发展中占有举足轻重的位置[16-20]。当前，有关思茅松天然林林分直径结构的研究主要集中在林分直径结构分布规律、动态变化以及在林分直径结构分布模型的基础上揭示拟合函数参数与环境因子的关系等方面[21-22]。尤其缺乏分别对思茅松天然成熟林内所有树种、思茅松和其他树种林分直径结构变化以及环境因子（林分、地形、土壤和气候）对其变化的影响的研究。

鉴于此，本研究以云南省普洱市45块思茅松天然成熟林样地为研究对象，采用Weibull分布函数分析样地内总体、思茅松和其他树种林分直径结构分布的变化规律，并借助典范对应分析（Canonical correspondence analysis，CCA）方法，揭示思茅松天然成熟林内总体、思茅松和其他树种林分直径结构分布变化与环境因子（林分、地形、土壤和气候）之间的关系，以期为思茅松天然林资源的科学经营管理、可持续开发利用提供理论参考。

1 研究区概况

云南省普洱市位于云南省西南部，地处N22°2′ ～ 24°50′、E99°9′ ～ 102°19′，总占地面积为45 385 km2，山地面积占98.3%，是云南省面积最大的（州）市，海拔在317 m～3 370 m之间。由于受到亚热带季风气候的影响，年均气温在15℃～20.3 ℃之间，年无霜期在315 d以上，年均降水量在1 100 mm～2 780 mm之间，温暖湿润。全市森林覆盖率超过67%，是云南省重点林区，思茅松是主要树种。普洱市是镶嵌在云南省的一颗绿色明珠，素有绿海明珠、天然氧吧的美誉。本研究结合普洱市的实际情况，选取墨江县通关镇( SiteⅠ) 、思茅区云仙乡( SiteⅡ) 和澜沧县糯福乡( SiteⅢ)作为研究位点（见图1），研究位点基本情况见表1。

2 研究方法

2.1 数据调查和收集

在3个研究位点分别调查15块、共45块面积分别为20 m×30 m的思茅松天然成熟林典型样地（表2）。其中，部分样地除了思茅松外，还伴生有其他树种，诸如，滇青冈Cyclobalanopsis glauca、艾胶树Glochidion lanceolarium、茶梨Anneslea fragrans、 密 花 树 Rapanea nerrifolia、水锦树 Wendlandia uvariifolia、红木荷 Schima wallichii等。对样地内乔木进行每木检尺，记录树种名称，实测胸径、树高。采集土壤样品，记录样地基本地形因子（海拔、坡度、坡向），并从环境气象网站( http://www.worldclim.org)获取三个研究位点的生物气候数据，该数据基于1970—2000年30年间的最小月均温、最大月均温和平均月均温以及月平均降水量等数据计算而来。

2.2 数据整理和测定

对获取的研究位点4类环境因子数据进行整理、测定。基于各样地每木检尺数据，计算得到林分平均年龄（Age）、郁闭度（YBD）、林分平均高（Hm）、林分优势高（Ht）、林分密度指数（SDI） 和地位指数（SI），并构建林分因子数据矩阵。构建海拔（Alt）、坡度（SLO） 和坡向（ASPD）地形因子数据矩阵。测定土壤样品常规8项指标：土壤 pH 值（pH）、土壤有机质含量（OM）、全氮（TN）、全磷（TP）、全钾（TK）、水解性氮（HN）、有效磷（YP） 和速效钾（SK），并构建土壤因子数据矩阵。对获取的19个气候因子：年均温（b1）、气温年较差（b2=最热月均温-最冷月均温）、等温性（b3= b2/b7）、季节性温度（b4）、最热月最高温（b5）、最冷月最低温（b6）、气温年较差（b7=b5-b6）、最湿季均温（b8）、最干季均温（b9）、最热季均温（b10）、最冷季均温（b11）、年降水（b12）、降水最大月降水（b13）、降水最小月降水（b14）、季节降水变异系数 b15）、最湿季降水（b16）、最干季降水（b17）、最热季降水（b18）、最冷季降水（b19）进行数据分析，并构建气候因子数据矩阵。

图1 研究位点位置示意Fig.1 The location of study sites

表1 研究位点基本情况Table 1 The basic information of study sites

2.3 数据计算与分析

2.3.1 林分直径结构的Weibull分布函数拟合

采用Weibull分布函数拟合林分直径结构变化，Weibull分布函数公式为：

式中：a为位置参数，b为尺度参数，c为形状参数；

X为径阶值，Y为不同径阶的株数累积值。

Weibull分布函数中的3个参数与林分特征因子有关。其中，a是指林分最小直径，它随着林分平均胸径、林龄、立地增大而增大；b是指林分直径分布范围，它随林分平均胸径、林龄、立地、密度增大而增大；c决定了林分直径分布偏度，是分析林分直径分布动态的重要依据之一，也是Weibull分布函数中具有实质意义的参数。

2.3.2 CCA排序分析

典范对应分析方法(CCA)是一种把对应分析与多元回归分析结合起来的直接排序方法，能够直接分析多个自变量与因变量的关系，是专门为分析植被与环境因子之间的关系而设计的方法，需要借助植被与环境因子两个数据矩阵来完成[23-25]。本研究采用CANOCO Version 4.5软件分别对样地总体、思茅松和其他树种林分直径结构拟合函数参数与林分因子、地形因子、土壤因子、气候因子进行CCA 排序分析，根据CCA排序轴的前两轴分别制作总体、思茅松和其他树种林分直径结构拟合函数参数与4类环境因子的二维排序图，并分析各林分直径结构拟合函数参数与环境因子之间的关系。

表2 样地基本特征表Table 2 The basic information for the plots

3 结果分析

3.1 林分直径结构的分布拟合

3.1.1 总体林分直径结构的分布拟合

从三个位点思茅松天然成熟林总体林分直径结构Weibull分布函数拟合来看，拟合方程的决定系数（R2）均在0.99以上，分别达到了0.998 9、0.998 7和0.998 6；a值分布区间为92.827 2～96.105 9，b值在0.076 5～0.080 0之间，c值在1.609 6～1.809 3之间，均方差MSE在5.726 6～10.969 8之间；其中，墨江县的拟合效果最好，决定系数（R2=0.998 9）最大，均方差（MSE=5.726 6）最小；总体而言，决定系数R2为0.998 7，MSE为7.743 3（表3）。此外，拟合参数a、b、c的F检验显著性均大于0.05（表4），可见，3个位点思茅松天然成熟林内总体林分最小直径、林分直径分布范围、林分直径结构分布偏度的差异均不显著。

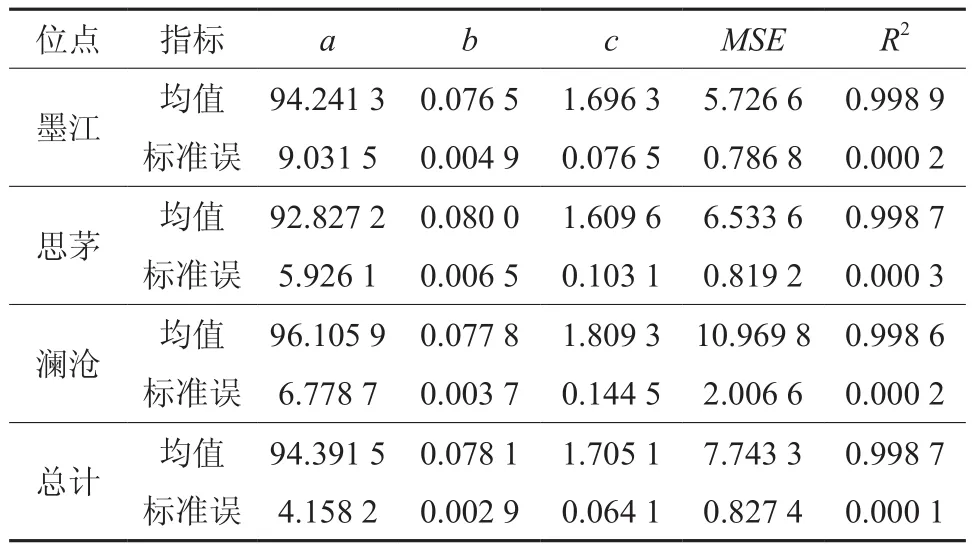
表3 总体林分直径结构Weibull拟合函数参数分析表Table 3 Weibull fitting function parameters of the overall stand diameter structures

表4 总体林分直径结构Weibull拟合函数参数单因素方差分析表Table 4 The ANOVA of Weibull fitting function parameters for overall stand diameter structures

3.1.2 思茅松林分直径结构的分布拟合

从3个位点思茅松天然成熟林思茅松林分直径结构Weibull分布函数拟合来看，拟合方程的决定系数（R2）均在0.99以上，分别达到了0.998 2、0.998 3和0.997 3；a值分布区间为48.369 7～84.996 0，b值在0.053 2～0.064 2之间，c值在2.096 3～2.662 7之间，均方差MSE在2.379 0～3.801 5之间；思茅地区的拟合效果最好，决定系数（R2=0.998 3）最大；总体的决定系数R2为0.997 9，MSE为3.0574（表5）。拟合参数a、b、c的F检验显著性均大于0.05（表6）。可见，3个位点思茅松天然成熟林内思茅松林分最小直径、林分直径分布范围、林分直径结构分布偏度的差异均不显著。

表5 思茅松林分直径结构Weibull拟合函数参数分析表Table 5 Weibull fitting function parameters of the Simao pine stand diameter structures

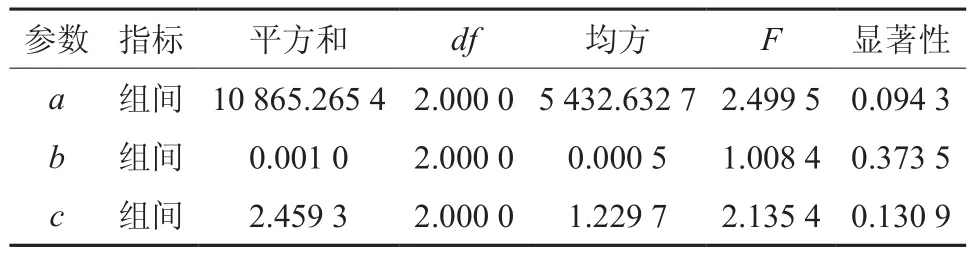
表6 思茅松林分直径结构Weibull拟合函数参数单因素方差分析表Table 6 The ANOVA of Weibull fitting function parameters for Simao pine stand diameter structures

3.1.3 其他树种林分直径结构的分布拟合

从3个位点思茅松天然成熟林其他树种林分直径结构Weibull分布函数拟合来看，拟合方程的决定系数（R2）均在0.99以上，分别达到了0.998 8、0.998 6和0.999 2；a值分布区间为35.999 0～52.031 0，b值在0.105 8～0.132 1之间，c值在1.972 2～2.5664之间，均方差MSE在0.848 5～2.482 3之间；澜沧县的拟合效果最好，决定系数（R2=0.999 2）最大；总体而言，决定系数R2为0.998 9，MSE为1.657 9（表7）。拟合参数a的F检验显著性为0.032 3，小于0.05；拟合参数b、c的F检验显著性分别为0.213 7、0.237 9，均大于0.05（表8）。可见，三个位点思茅松天然成熟林内其他树种林分最小直径呈现出较显著差异，而其林分直径分布范围、林分直径结构分布偏度的差异较不显著。

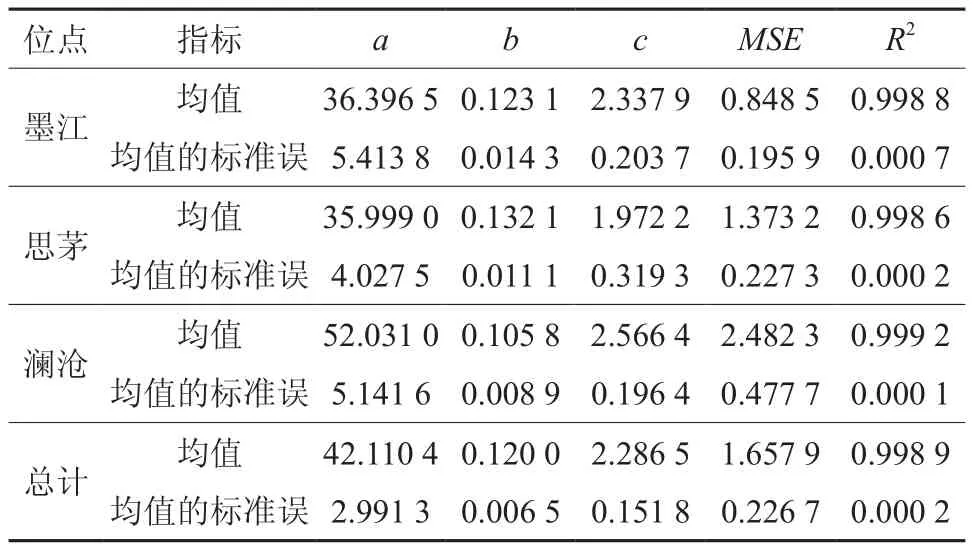
表7 其他树种林分直径结构Weibull拟合函数参数分析表Table 7 Weibull fitting function parameters of the other tree species stand diameter structures

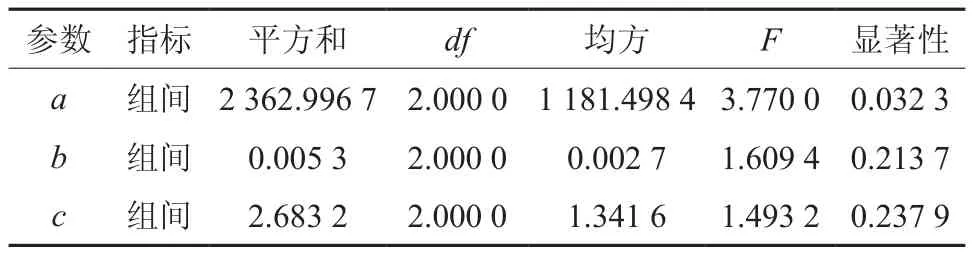
表8 其他树种林分直径结构Weibull拟合函数参数单因素方差分析表Table 8 The ANOVA of Weibull fitting function parameters for other tree species stand diameter structures

3.2 林分直径结构变化CCA排序分析

3.2.1 环境因子CCA排序结果

从林分、地形、土壤和气候因子与林分直径结构Weibull分布函数拟合参数进行CCA排序分析可以看出，各类环境因子的CCA排序结果较好。其中，林分、地形、土壤和气候因子排序轴的第一轴分别解释了林分直径结构变化55.0%、46.5%、43%和59.1%的信息量，前两个排序轴分别累计解释其变化的77.2%、81.9%、73.1%和74.5%，可见排序轴的前两轴，尤其是第一轴，较好的反映了林分直径结构随各类环境因子的变化。从第一排序轴解释的信息量来看，气候因子解释了最多的林分直径结构变化信息，林分因子次之，土壤因子最小。

表9 环境因子CCA排序参数表†Table 9 The parameters of CCA for environmental factors

3.2.2 林分因子与林分直径结构拟合函数参数CCA排序分析

从表10可以看出，林分平均高与排序轴第一轴具有最大相关性，为0.682 0，林分优势高次之。郁闭度与第二轴具有最大相关性，为0.532 8。且所有林分因子均与第一、二轴呈现出正相关。地位指数与第三轴存在最大相关性，为-0.265 3。所有林分因子与第四轴的相关性均在0.17以下，相关性较弱。林分年龄与四个排序轴第一轴具有最大相关性，为0.481 5。同时，前两轴的累计解释量达到77.2 %（见表9），说明第一、二排序轴较好的拟合了林分直径结构拟合函数参数与各林分因子的关系。可见，对思茅松天然成熟林林分直径结构影响较显著的林分因子是郁闭度、林分平均高和林分优势高。

表10 林分因子与Weibull拟合参数CCA排序轴关联系数表†Table 10 The correlation coefficients between the stand factors and CCA axes of Weibull fitting parameters

根据前两轴绘制的二维排序图（见图2-a）可以看出，第一轴从左至右，郁闭度、林分密度指数、林分年龄等6个林分因子不断增大；第二轴从下往上，地位指数、林分平均高、林分优势高等6个林分因子逐渐上升。思茅松天然成熟林内其他树种林分直径结构拟合函数a参数（ao）在郁闭度、林分年龄最大时取得最大值。思茅松林分直径结构拟合函数c参数（cp）受林分平均高影响较大。总体林分直径结构拟合函数a参数（at）、b参数（bt）和其他树种林分直径结构拟合函数b参数（bo）聚集在一起，说明三个参数的变化趋势相似，它们在相似的条件下取得最大值，即郁闭度偏小、林分平均高、地位指数等林分因子最小时取得最大值。思茅松林分直径结构拟合函数a参数（ap）、b参数（bp）、总体林分直径结构拟合函数c参数（ct）和其他树种林分直径结构拟合函数c参数（co）并没有体现出类似的规律。

3.2.3 地形因子与林分直径结构拟合函数参数CCA排序分析

从表11可以看出，坡度与排序轴第一轴具有最强相关性，为0.386 1，海拔、坡度与第一轴呈现出正相关，而坡向与之呈现出负相关。海拔与第二轴具有最大相关性，为-0.285 9，海拔、坡向与第二轴呈现出负相关，而坡度与之呈现出正相关。坡向与第三轴具有最大相关性，为-0.275 8，海拔、坡度与第三轴呈现出正相关，坡向与之呈现出负相关。而各地形因子与第四轴无相关性。同时，前两轴的累计解释量达到81.9%（见表9），说明第一、二轴较好的拟合了个林分直径结构拟合函数参数与各地形因子的关系。可见，对思茅松天然成熟林林分直径结构影响较大的地形因子是海拔和坡度因子。

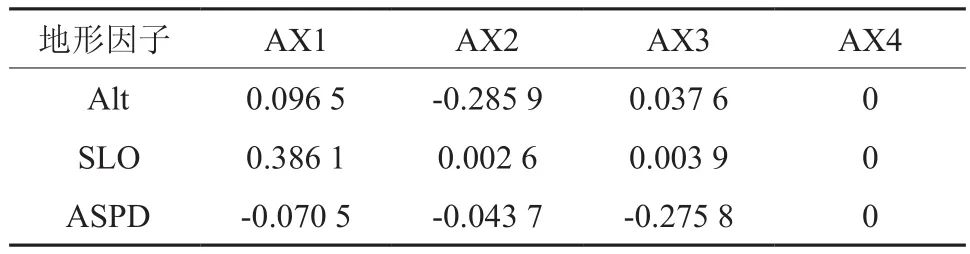
表11 地形因子与Weibull拟合参数CCA排序轴关联系数表†Table 11 The correlation coefficients between the topography factors and CCA axes of Weibull fitting parameters

根据前两轴绘制的二维排序图（见图2-b）可以看出，第一轴从左至右，坡向不断降低，海拔和坡度有不断上升的趋势；第二轴从下往上，坡向和海拔逐渐减小，坡度有逐渐增大的趋势。在海拔、坡向和坡度最小时，思茅松天然成熟林内其他树种林分直径结构拟合函数b参数（bo）取得最大值；在坡向最大、海拔和坡度最小的条件下，其他树种林分直径结构拟合函数c参数（co）取得最大值。总体林分直径结构拟合函数c参数（ct）受坡度影响较大；总体林分直径结构拟合函数a参数（at）与海拔有十分密切的关系；思茅松林分直径结构拟合函数b参数（bp）与坡向密切相关。

3.2.4 土壤因子与林分直径结构拟合函数参数CCA排序分析

从表12可以看出，全磷与排序轴第一轴具有最强相关性，为-0.576 5，全氮次之。除全钾外，其他土壤因子与第一轴的相关性均超过0.22。除土壤pH值外，其他土壤因子均与第一轴呈现出负相关。土壤pH值与第二轴具有最强相关性，为-0.263 9。土壤pH值、有机质含量、全磷、有效钾与第二轴呈现出正相关，全氮等与第二轴呈现出正相关。土壤pH值、全钾和有效磷与第三、四轴均呈现出正相关，而土壤有机质含量等与第三、四轴呈现出负相关。同时，前两轴的累计解释量达到73.1%（见表9），表明第一、二轴较好的拟合了林分直径结构拟合函数参数与各土壤因子的关系。可见，对思茅松天然成熟林林分直径结构影响较大的土壤因子是土壤pH值、全氮、全磷和水解性氮。

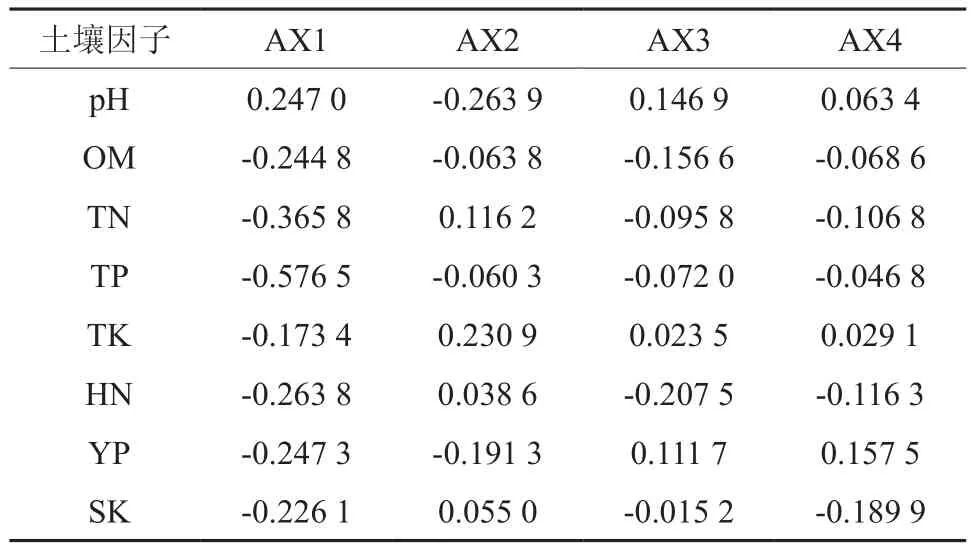
表12 土壤因子与Weibull拟合参数CCA排序轴关联系数†Table 12 The correlation coefficients between the soil factors and CCA axes of Weibull fitting parameters

根据前两轴绘制的二维排序图（见图2-c）可以看出，第一轴从左至右，全磷、全氮、有效磷等土壤因子不断减小，土壤pH值不断变大；从第二轴从下往上，全磷、有效磷、土壤pH值、土壤有机质含量逐渐降低，全氮、全钾等土壤因子有逐渐上升的趋势。思茅松天然成熟林内总体林分直径结构拟合函数a参数（at）和b参数（bt）聚集在一起，说明两者具有相似的变化趋势，它们在相似的环境下取得最大值，即全磷、全氮最小、土壤pH值中等的条件；总体林分直径结构拟合函数c参数（ct）和思茅松林分直径结构拟合函数c参数（cp）位置很近，说明两个参数的变化趋势相似，即速效钾、水解性氮最大，土壤pH值最小时，两者取得最大值。而其他树种林分直径结构拟合函数a参数（ao）、c参数（co）等参数并没有体现出类似的规律性。

3.2.5 气候因子与林分直径结构拟合函数参数CCA排序分析

从表13可以看出，气候因子b17与排序轴第二轴具有最强负相关，为-0.486 4。b3与第二轴具有最强正相关，为0.424 2。而气候因子b4、b14和b19与第二轴的相关性也大于0.4。气候因子b2、b12、b15与第二轴的相关性、b8与第四轴的相关性和b16与第三轴的相关性均大于0.3。所有气候因子与第一轴的相关性均小于0.075。同时，前两轴的累计解释量达到74.5%（见表9），表明，第一、二轴较好的拟合了林分直径结构拟合函数参数与各气候因子的关系。因此，对思茅松天然成熟林林分直径结构影响较明显的气候因子有b2、b3、b4、b12、b14、b15、b16、b17 和 b19。

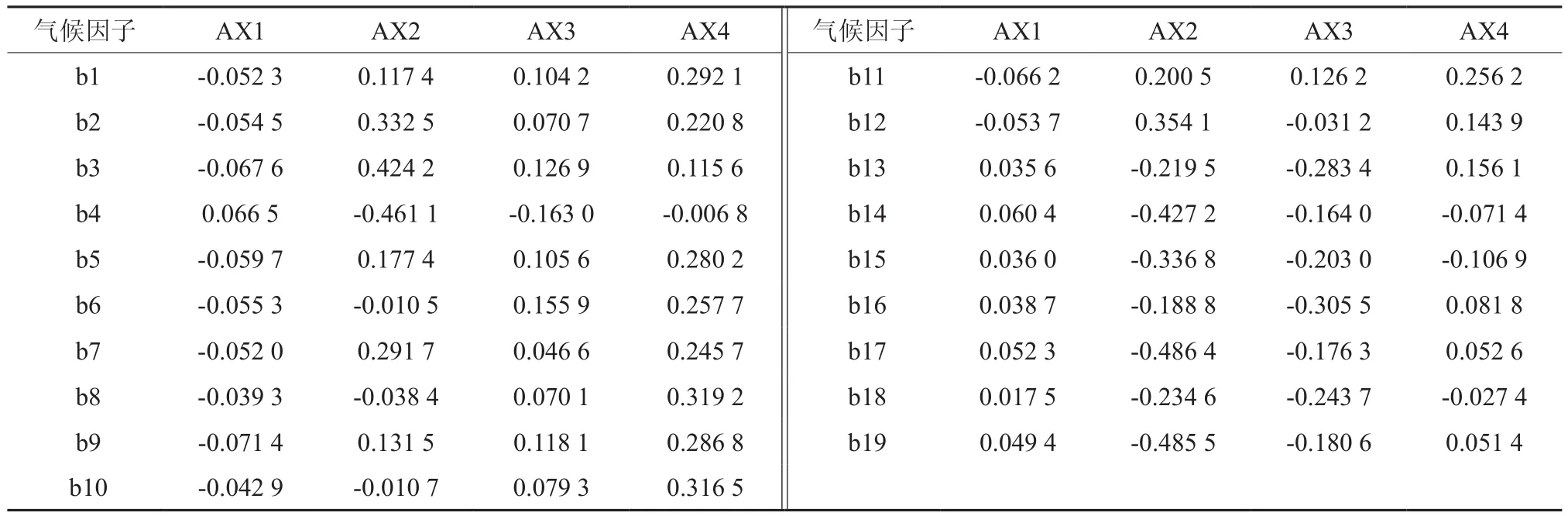
表13 气候因子与Weibull拟合参数CCA排序各轴关联系数†Table 13 The correlation coefficients between the climate factors and CCA axes of Weibull fitting parameters

根据前两轴绘制的二维排序图（见图2-d）可以看出，第一轴从左至右，b1、b2、b3、b5、b6、b8等气候因子不断减小，b4、b13、b14、b15等气候因子有不断增大的趋势；从第二轴从下往上，b4、b6、b8、b13、b14、b15等气候因子逐渐降低，b1、b2、b3、b5、b7等气候因子逐渐增加。思茅松天然成熟林内思茅松林分直径结构拟合函数b参数（bp）、c参数（cp）和总体林分直径结构拟合函数c参数（ct）聚集在一起，说明三个参数的变化趋势相似，它们在相似的条件下取得最大值，即b4、b6、b8、b13、b14等气候因子偏小，b1、b2、b3、b5较中等时，三个参数取得最大值。而思茅松林分直径结构拟合函数a参数（ap）并没有体现出类似的规律性。林内其他树种林分直径结构拟合函数a参数（ao）、b参数（bo）和c参数（co）受气候因子b6、b8和b10影响较大。

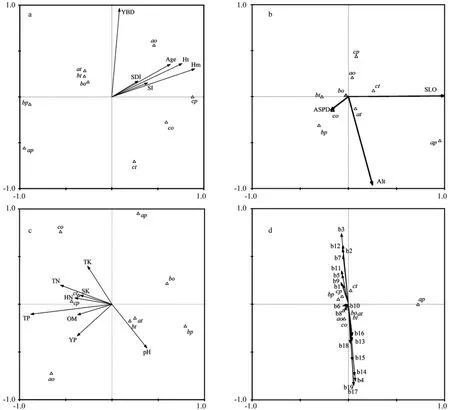
图2 环境因子CCA二维排序图Fig.2 CCA two-dimensional diagrams for four types of environmental factors

4 结论和讨论

本文充分利用Weibull分布函数可塑性大、准确性高、实用性强等独特的优越性[1]，研究思茅松天然成熟林内总体、思茅松和其他树种林分直径结构规律，并通过对Weibull拟合函数参数与4类36个环境因子关系的CCA排序分析，分析各参数的变化规律，主要得到以下几个结论。

(1) 从Weibull分布函数拟合结果来看，3个研究位点总体、思茅松和其他树种的林分直径分布范围、林分直径结构分布偏度的差异均不显著；而3个研究位点的其他树种林分最小直径呈现出较显著的差异。

(2) 林分直径结构Weibull拟合函数参数CCA排序分析结果较好的反映了林分直径结构随环境因子的变化规律。4类环境因子中，气候因子最好的解释了思茅松天然成熟林林分直径结构的变化，林分因子次之。

(3) 郁闭度、林分平均高和林分优势高，海拔与坡度，全氮和全磷，等温性、季节性气温变化、最小月降水、最干季降水和最冷季降水分别是影响林分直径结构的林分、地形、土壤和气候因子中的主要因素。

(4) 从二维排序图来看，林内总体、思茅松和其他树种Weibull分布函数拟合参数的变化与气候因子密切相关。林分总体与思茅松的林分直径结构拟合函数c参数的位置相对较近，表明林分总体与思茅松的林分直径结构分布呈现较为一致的变化趋势。

目前，国内在Weibull分布函数的基础上研究思茅松天然成熟林林分直径结构变化规律还是比较少的，特别是有关林分直径结构环境解释的更是少有报道。Weibull分布函数因其具有足够的灵活性、参数的生物学意义明显、参数以求解等优点，能成功用于模拟林分直径结构[26]，本研究采用Weibull分布函数对思茅松天然成熟林分总体、思茅松和其他树种林分直径结构进行拟合，各研究位点总体、思茅松和其他树种的拟合方程决定系数（R2）在0.997 3～0.999 2，说明各研究位点总体、思茅松和其他树种林分直径分布均符合Weibull分布，同时也再次验证了Weibull分布函数在林分直径结构的研究中具有很强的实用性。此外，本文借助CCA排序分析解释拟合函数参数与36个环境因子的关系，得出林分总体、思茅松和其他树种拟合函数参数的变化与气候因子密切相关，且总体林分直径结构与思茅松的变化趋势较为一致。欧光龙等有关思茅松天然林胸径与树高结构的变化研究中采用Weibull拟合思茅松天然林整体林分直径结构的基础上，用逐步回归的方法分析拟合了函数参数与包含林分因子和土壤因子的15个环境因子的相关关系[23]。而本研究更为全面考虑环境因素对林分直径结构分布的影响，并且考虑了思茅松天然林的树种组成差异，分别分析了林内总体、优势树种思茅松以及其他树种的林分直径结构变化，以及环境因子对其结构的影响，从而为更为科学合理经营思茅松天然林提供非常重要的参考。当然，环境因子之间会相互作用从而影响林分生长，从而影响林分直径结构变化，本研究仅分别分析4类环境因子对林分直径结构的影响，而未考虑环境因子间相互作用对林分直径结构的影响，这有待在今后的研究中进一步完善。

[1]董文宇, 邢志远, 惠淑荣,等.利用Weibull分布描述日本落叶松的直径结构[J].沈阳农业大学学报, 2006, 37(2):225-228.

[2]宁小斌, 李永亮, 刘晓农.基于Weibull分布的林分结构可视化模拟技术研究[J].中南林业调查规划, 2012, 31(2):13-17.

[3]黄家荣, 孟宪宇, 关毓秀.马尾松人工林直径分布神经网络模型研究[J].北京林业大学学报, 2006, 28(1):28-31.

[4]国 红, 雷渊才.蒙古栎林分直径Weibull分布参数估计和预测方法比较[J].林业科学, 2016, 52(10):64-71.

[5]闫东锋, 侯金芳, 张忠义,等.宝天曼自然保护区天然次生林林分直径分布规律研究[J].河南科学, 2006, 24(3):364-367.

[6]黄家荣.Weibull分布在马尾松人工林中的适用性研究[J].贵州林业科技, 2000(1):7-13.

[7]王香春, 张秋良, 春 兰,等.大青山落叶松人工林直径分布规律的研究[J].山东农业大学学报(自然科学版), 2011,42(3): 349-355.

[8]朱光玉, 康 立.桤木幼龄林直径结构规律分析[J].湖南林业科技, 2016, 43(5):1-6.

[9]张 文, 高天雷.马尾松林分直径结构研究[J].四川林勘设计,2001(2):26-30.

[10]Diamantopoulou M J, Özçelik R, Crecente-Campo F, et al.Estimation of Weibull function parameters for modelling tree diameter distribution using least squares and artificial neural networks methods[J].Biosystems Engineering, 2015, 133:33-45.

[11]铁 牛.长白落叶松人工林林分直径分布研究[J].林业资源管理, 2014(6):95-98.

[12]单振明, 王 鲲.樟子松人工林林分直径分布规律的研究[J].林业科技情报, 2013, 45(1):36-37.

[13]胥 辉, 屈 燕.思茅松天然次生林林分直径结构规律的研究[J].西南林业大学学报, 2001, 21(4):193-195.

[14]云南森林编写委员会.云南森林[M].昆明:云南科技出版社&中国林业出版社, 1988.

[15]西南林学院, 云南省林业厅.云南树木图志[M].昆明:云南科技出版社, 1988.

[16]李 浩, 张 超, 许彦红.思茅松空间分布特征研究[J].西南林业大学学报, 2015,35(1):47-51.

[17]翁海龙, 陈宏伟, 段安安.思茅松高产脂优树选择[J].西北林学院学报, 2010, 25(3):71-74.

[18]温庆忠, 赵远藩, 陈晓鸣,等.中国思茅松林生态服务功能价值动态研[J].林业科学研究, 2010, 23(5):671-677.

[19]岳 锋,杨 斌.思茅松林碳汇功能研究[J].江苏农业科学,2011, 39(5):467-469.

[20]张文勇.思茅松人工幼龄林和中龄林直径分布规律的研究[J].安徽农业科学, 2011, 39(13):7736-7737.

[21]姚能昌, 段爱国, 唐军荣.思茅松天然林林分直径结构动态变化[J].西南林业大学学报, 2012, 32(2):49-52.

[22]欧光龙, 王俊峰, 胥 辉,等.思茅松天然林胸径与树高结构的变化[J].中南林业科技大学学报, 2014, 34(1):37-41.

[23]Braak C J F T.Canonical correspondence analysis: a new eigenvector method for multivariate direct gradient analysis[J].Ecology, 1986, 67:1167-1179.

[24]郭晋平.森林景观生态研究[M].北京:北京大学出版社, 2001.

[25]丁献华, 毕润成, 闫 明.基于CCA排序的霍山森林植物功能型划分[J].重庆师范大学学报(自然科学版),2011,28(1):64-67.

[26]孟宪宇.使用Weibull函数对树高分布和直径分布的研究[J].北京林业大学学报, 1988(1):40-48.