考虑负荷不确定性的微电网优化调度研究

,,

(1.国家电网公司西南分部，四川 成都 610041；2.电子科技大学，四川 成都 611731)

0 引 言

近年来随着世界经济的快速发展，世界各国对能源的需求不断增大，一方面，造成全球能源供应的日益紧张；另一方面，也带来了诸如气候恶化、温室效应等严重的环境问题。因此，提升新能源利用比例、改善能源结构、缓解能源利用与环境保护之间的矛盾，已成为当前能源及电力体系的发展共识和必然趋势。

微电网(Microgrid)是一种新型的能源网络化供应与管理结构，由分布式电源、储能装置、控制装置及负荷组成。相对于传统电网发电系统，微电网可有效实现大规模分布式电源的灵活接入与高效利用，在降低能耗和减少环境污染的同时，也提高了系统的可靠性与灵活性。

随着微电网技术的不断成熟，微电网功能和结构日趋复杂，对微电网运行的经济、环保、可靠性的要求也不断提高[1]。如何改善提升其运行的经济性与环保性，已成为当前国内外微电网优化运行的研究热点。文献[2]建立了包括建设及折旧费用、维护费用、无功补偿成本及政府新能源补贴的经济性目标，而微电网的环保性通过系统的污染物排放惩罚来衡量；通过基于改进的遗传算法对优化模型进行求解。文献[3]将微电网的环保性用环境成本来计算，将其与经济性目标列入同一个目标函数；其经济性目标函数考虑了并网时的运行成本、运行维护成本、MT的燃料成本及制冷制热收益；利用改进的鸡群算法对优化模型进行求解。但上述研究仅将微电网环保性改善作为首要前提，未同时考虑运行方式对于微电网经济性的影响。文献[4]将经济成本及CO2的排放量作为调度优化的两个目标，采用将模糊矩阵引入传统粒子群算法中的方法，协同优化两目标。文献[5]在以运行成本最小为优化目标的基础上，考虑了风力发电及光伏发电的功率预测存在误差，通过贝塔分布拟合出有误差的可再生能源发电功率曲线，研究其误差大小对微电网稳定经济运行的影响。但上述研究仅针对固定发电单元进行优化，未考虑多种能源接入的协调问题。

为解决上述问题，搭建了含风力、光伏、燃气轮机、燃料电池及蓄电池等多供能主体的微电网模型，在综合考虑能量供需平衡、爬坡速率约束及蓄电池充放电容量限制条件下，运用混合整数规划优化方法，建立了考虑负荷的不确定性因素下以离网型微电网为主的微电网经济调度模型，并针对多种典型负荷场景对建立的模型准确性进行了验证。

1 分布式电源的数学模型

1.1 风机发电模型

风机的发电量由风速决定，已知风速即可求出出力。风机出力与风速的关系可近似表示为

(1)

式中：Pr为风机额定功率；V为风力发电机所受的风速；VO为额定风速；a和b为风机出力曲线的拟合参数，其计算公式为

(2)

式中：VI为切入风速；Vr为切出风速。

1.2 光伏发电模型

光伏发电的发电量由光照强度及环境温度决定，在标准测试条件下，光伏电池的输出功率为

PPV=PSTC(GT/GSTC)·[1-k(Tc-Tr)]

(3)

式中：PSTC为标准测试条件(即太阳光照强度1000 Lux，环境温度25℃时)下的最大测试功率；GT为运行时的光照强度；GSTC为标准测试条件下的光照强度；k为功率温度系数，取-0.47[6]；Tr为参考温度；Tc=Te+30·(GT/1 000)，Te为运行时的环境温度。

1.3 燃料电池模型

燃料电池是一种将燃料和氧化剂中的化学能不经过燃烧直接转换为电能的装置，因此燃料电池不受卡诺循环的限制。因其能量转换效率高、启动速度快、体积小、污染小等优点，广泛应用于微电网。燃料成本的计算如式(4)。

CFC=(CM/L)·∑(PFC(t)·Δt/ηFC(t))

(4)

式中：CM为天然气的市场价格，取2.5元/m3[7]；L为天然气的低热值，取9.7 kWh/m3，PFC(t)为t时刻的净输出电功率；ηFC(t)为燃料电池的效率。

1.4 燃气轮机模型

微型燃气轮机是一种小型的热动装置，功率一般在30～250 kW，以天然气、甲烷、汽油等作为燃料，因其可靠性高、体积小、污染小等优点，使其具有广泛的商业发展前景，适用于各种环境的微电网。

燃汽轮机的燃料成本计算与燃料电池的相近：

CFC=(CM/L)·∑(PFC(t)·Δt/ηFC(t))

(6)

1.5 蓄电池模型

蓄电池具有电能双向流动、可兼顾容量和功率需求、优异的环保效益等优势，蓄电池等储能装置在微电网中占据着重要作用。特别是在微电网工作于离网模式时，由于失去了与大电网交互能量的途径，蓄电池作为既可充电亦可放电的装置，可暂时替代大电网的部分功能，所以蓄电池在微电网中的应用至关重要。

蓄电池充放电时主要涉及其剩余容量的计算，通过计算其剩余容量，即可知道何时能充电或放电，以及充放电电量。蓄电池t时刻的剩余容量，与前一时刻的剩余电量及充放电量相关，计及蓄电池的自放电率与充放电效率，其剩余容量计算公式如下[8]。

放电时,P(t)>0:

(6)

充电时，P(t)<0:

SOC(t)=SOC(t-1)(1-δ)-PSB(t)ηSB

(7)

式中：SOC(t)为蓄电池t时刻的容量；δ为蓄电池的自放电率；PSB为蓄电池t时刻的充放电量；ηSB为蓄电池的充放电效率。

通过建立各分布式电源发电功率的数学求解模型，即可根据现有的可测量的数据求解分布式电源的发电功率。进而通过建立微电网的优化调度模型，可优化各分布式电源的出力情况。

2 微电网的优化模型

2.1 目标函数

下面将综合考虑到微电网运行的经济性与环保性，且微电网处于离网模式下的优化模型，不考虑微电网与外网交互的成本。目标函数可分为经济性与环保性。

1)经济性

考虑微电网一天内的发电成本最低，其中发电成本包括燃料成本、投资折旧成本、运行维护成本。其目标函数表达式为

f(t)=f1(t)+f2(t)+f3(t)

(8)

式中，f1(t)为燃料成本，其计算公式为

f1(t)=CFC+CMT

(9)

式中，CFC、CMT分别为燃料电池及微型燃气轮机的燃料成本。

f2(t)为设备投资折旧成本，其计算公式可表示为[9]

(10)

式中，Pi(t)为第i个分布式电源的在t时刻的出力；CAZ,i为第i个分布式电源的单位容量安装成本；ki为第i个分布式电源的容量因数；r为年利率；q为第i个分布式电源投资回收年限。

f3(t)为设备运行维护成本，其计算公式可表示为[10]

(11)

式中，KWH,i为第i个分布式电源的单位电量运行维护成本系数。

2)环保性

通过将分布式电源排放的污染物的量，转化为其因排放污染物所需付出的环境保护成本来计算。

(12)

式中，M为排放的气体的种类总数；CHB(m)为每种排放的气体对应的环保治理费用；kmi为第i个设备排放第m种气体时的排放因子。

2.2 约束条件

1)功率平衡约束

任意时刻各分布式电源的出力之和需满足微电网的负荷需求。

(13)

2)各分布式电源的出力约束

任意时刻分布式电源的出力不能超出自身最大、最小功率的限制[15]。

Pi(t)min≤Pi(t)≤Pi(t)max

(14)

式中，Pi(t)min与Pi(t)max分别为第i个分布式电源出力的最大值与最小值。

3)MT的爬速率约束

增出力时，有：

PMT(t)-PMT(t-1)≤Pup,MT

(15)

前后两个调度时间的出力之差应小于其爬坡速率。

减出力时，有：

PMT(t-1)-PMT(t)≤Pdown,MT

(16)

式中，Pup,MT、Pdown,MT分别为微型燃气轮机增出力和减出力时单位时间内的变化功率限制。

4)蓄电池的相关约束

蓄电池在充电或者放电时，每次充放电的电量有所限制；其充放电后，蓄电池的容量要保持在限值之内；在一天的调度周期内，蓄电池的始末容量需保持相同。

所建立的蓄电池充电模型，选择了最大输出功率为100 kW,单位时间内的输出功率不超过最大输出功率的20%。其表达式为

(17)

式中：P+为蓄电池放电时的功率；P-为蓄电池充电时的功率；PSB,max为蓄电池的最大输出功率。

蓄电池总的容量还需要控制在一定范围内。在蓄电池充电的时候，其充电后的最大容量不能超过其自身的最大容量。蓄电池在放电的时候，如果放电深度过大，会降低蓄电池的使用寿命，所以需限制放电后最小剩余容量，即将其规定为放电后蓄电池的容量不小于最大容量的20%。其数学表达式为

SOCSB,max(t)·20%≤SOCSB(t)≤SOCSB,max(t)

(18)

式中：SOCSB,max(t)为蓄电池充放电时可以充放电容量的最大值；SOCSB(t)为t时刻蓄电池的容量值。

为满足蓄电池循环调度的前提，蓄电池在一个周期的充放电电量需满足始末平衡。即可表示为蓄电池在一个调度周期内充放电电量相同：

∑SOCSBC=∑SOCSBF

(19)

蓄电池可以工作于充电、放电两种状态下，为求解模型方便，引入状态开关变量Oc(t)、Of(t)来表示蓄电池在t时刻的充放电状态。在t时刻，Oc(t)值为1则表示充电，Of(t)值为1则表示放电。则式(17)、式(18)、式(19)可表示为

(20)

式中，

Oc(t)+Of(t)=1

(21)

在蓄电池参与优化调度时，如频繁地转换蓄电池的充放电状态，也会导致蓄电池的使用寿命变短。为延长蓄电池的使用寿命，还需对蓄电池的充放电次数进行限制，故引入状态变量NSB(t)，对其进行如下定义：

NSB(t)=|Oc(t)-Oc(t-1)|

(22)

式中，Oc(t-1)为蓄电池上一个调度时间的开关变量状态值。蓄电池在一个调度周期内充放电次数的约束条件可表示为

(23)

式中，NSB,max为蓄电池一个调度周期内最大的充放电转换次数。

3 算例及分析

3.1 微电网系统结构

采用 9节点的辐射状的微电网验证所建模型，在满足系统约束条件下实现微电网能量优化分配。微电网结构如图1所示。考虑微电网负载容量，设置风电单元容量、光伏单元容量、微型燃气轮机单元容量、燃料电池单元容量及储能单元容量分别为20 kW、12 kW、65 kW、40 kW、120 kW。

3.2 模型参数

5个负荷曲线示意如图2所示。

主要各分布式电源单元参数设置见表1。

图1 微电网结构

设备名称参数名称数 值微型燃气轮机出力上限/kW向上爬坡速率/(kW·h-1)向下爬坡速率/(kW·h-1)安装成本/(万元·kW-1)使用年限/年运行维护成本/(元·kWh-1)天然气价格/(元·m-3)天然气低热值/(kWh·m-3)651201001.35100.082.59.7燃料电池出力上限/kW安装成本/(万元·kW-1)使用年限/年运行维护成本/(元·kWh-1)天然气价格/(元·m-3)天然气低热值/(kWh·m-3)402.8100.12.59.7蓄电池额定功率/kW额定容量/kWh安装成本/(万元·kW-1)使用年限/年运行维护成本/(元·kWh-1)最大剩余容量/%最小剩余容量/%充电效率放电效率自放电率201000.066 7100.083 2100100.90.90.001

3.3 优化结果

利用Matlab求解优化模型，在满足各分布式电源的约束前提下，以提高微电网的经济性与可靠性为前提，得出各分布式电源在各时刻的出力。微电网的负荷往往具有随机性，每日的负荷曲线差异较大，需验证此优化调度模型能否满足各类型的负荷需求。根据图2选取负载曲线L1至L3进行优化验证，各负载情况下的系统运行优化结果见图3至图5。

图3 情况1时的优化结果

图3为系统在负荷曲线1 下的运行优化结果。根据图2负荷特性可知，在0:00—06:00期间为负荷的低谷时期，因此蓄电池切换至充电模型，其电能由风电及微型燃气轮机发电提供；14:00—17:00为负荷高峰期，且系统的负荷需求高达140 kW，此时微型燃气轮机已满发，需利用蓄电池放电，满足系统的负荷需求，保障系统的稳定运行。

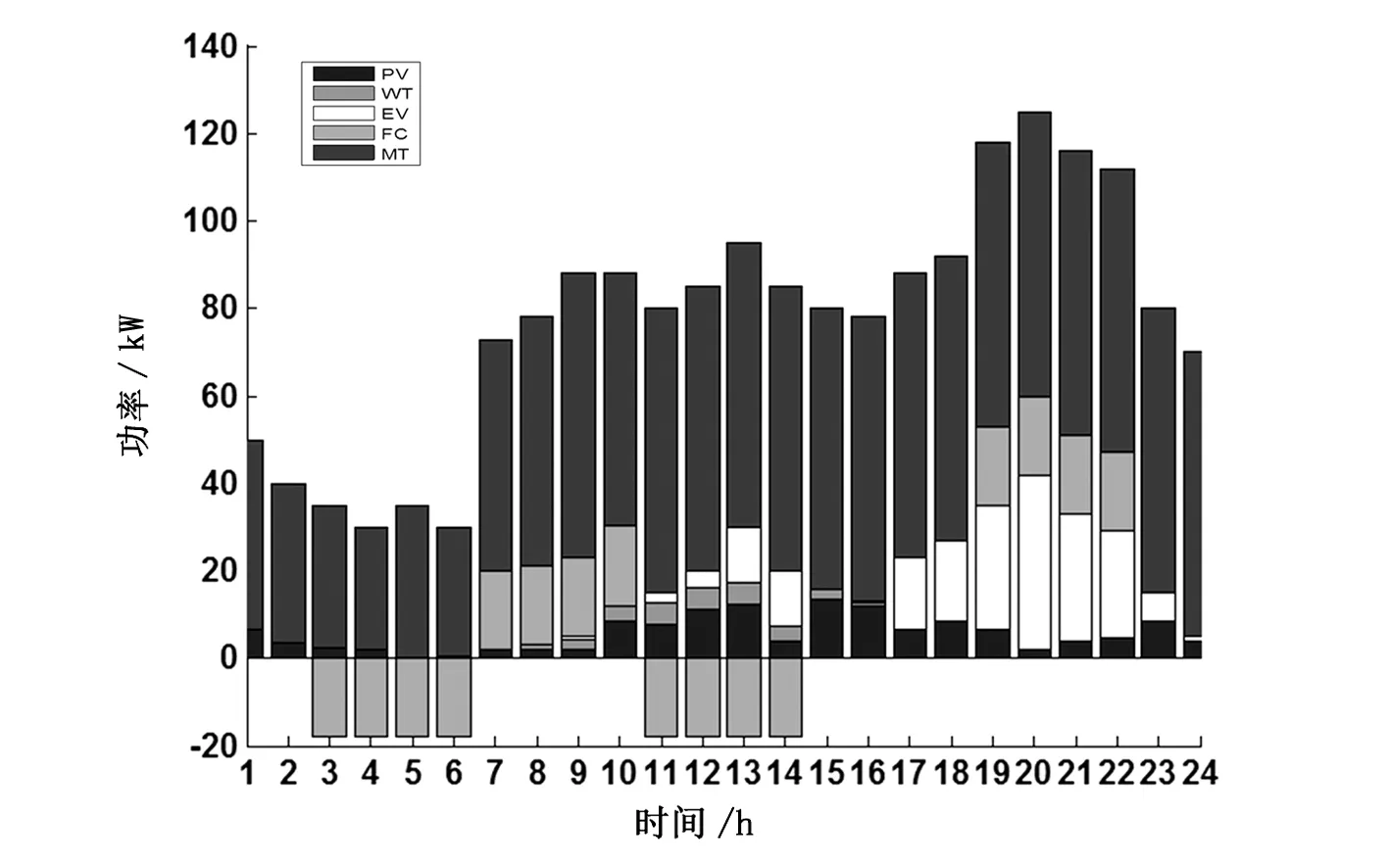
图4 情况2时的优化结果

图4为系统在负荷曲线2下的运行优化结果。负荷曲线2的负荷高峰期为19:00—22:00。如图4所示，此高峰时段微型燃气轮机已满发，需要蓄电池配合放电才可以满足系统负荷需求。由于该负荷条件下负荷高峰期时间出现较晚，此时蓄电池虽然已经过了两次充放电的转换，但依旧是满电量状态，因此在保证系统可靠性的同时保障了运行的经济性。

图5 情况3时的优化结果

图5为系统在负荷曲线3下的运行优化结果。负荷曲线3的负荷低谷期为0:00—04:00，因此蓄电池在较早时开始充电，随后根据负载变化不断切换放电、充电，但依旧保证了在负荷高峰期时达到满电量状态，从而满足负荷高峰期的系统调度需求。

4 结 语

建立了在保障微电网运行可靠性的前提下，以提高微电网的经济性与环保性为目标的优化调度模型，加大了蓄电池在微电网系统中的比重。所建立的模型包含风、光、微型燃气轮机、燃料电池、蓄电池，考虑能量供需平衡、爬坡速率约束及蓄电池充放电容量等约束条件。在3个负荷场景下，检验负荷的不确定性对微电网调度优化的影响，实验证明，所建立的微电网模型可有效工作于负荷不确定的模式。

[1] 杨毅,雷霞,叶涛,等. 考虑安全性与可靠性的微电网电能优化调度[J]. 中国电机工程学报,2014,34(19):3080-3088.

[2] 赵磊,曾芬钰,王霜,等. 基于经济性与环保性的微电网多目标优化调度研究[J]. 高压电器,2015,51(6):127-132.

[3] 胡汉梅,李静雅,黄景光. 基于改进鸡群算法的微电网优化运行研究[J]. 高压电器,2017,53(2):19-25.

[4] 邱晓燕,赵劲帅,史光耀,等. 基于HSMOPSO算法的微电网经济与环保协同优化方法[J]. 高电压技术,2017,43(4):1223-1230.

[5] 赵波,薛美东,陈荣柱,等. 高可再生能源渗透率下考虑预测误差的微电网经济调度模型[J]. 电力系统自动化,2014,38(7):1-8.

[6] 牛铭,黄伟,郭佳欢,等. 微网并网时的经济运行研究[J]. 电网技术,2010,34(11):38-42.

[7] 吴雄,王秀丽,王建学,等. 微网经济调度问题的混合整数规划方法[J]. 中国电机工程学报,2013,33(28):1-9.

[8] Gouveia C, Moreira J, Moreira C L, et al. Coordinating Storage and Demand Response for Microgrid Emergency Operation[J]. IEEE Transactions on Smart Grid, 2013, 4(4):1898-1908.

[9] 洪博文,郭力,王成山,等. 微电网多目标动态优化调度模型与方法[J]. 电力自动化设备,2013,33(3):100-107.

[10] 刘娇娇,王致杰,袁建华,等. 基于PSO算法的风光储微电网优化调度研究[J]. 华东电力,2014,42(8):1534-1539.