基于矩阵特征值分析和SOA优化模糊聚类的变压器故障诊断

，，，，，，，

(1.广东电网有限责任公司河源供电局，广东 河源 517000； 2. 广东工业大学自动化学院，广东 广州 510006)

0 引 言

油中溶解气体分析(dissolved gas analysis,DGA)利用在线监测数据对油浸式电力变压器进行故障诊断和状态评估，将定性的评估转变成具体量化的数据，是一种较为成熟的评估体系。目前应用最为广泛的油色谱分析方法是IEC三比值法[1]，但是该方法的故障编码固化，忽略边界效应，使得诊断的准确性受到限制[2]。近年来，随着机器学习和人工智能算法的发展，人工神经网络[3]、模糊数学[4]、粗糙集理论[5]、云理论[6]、核函数[7]以及支持向量机[8]等计算机方法被应用到变压器状态评估和故障诊断中。文献[3]充分利用BP神经网络处理非线性样本的能力，并与FPN网络结构相结合，在模糊推理的基础上，得出较好的故障诊断效果。文献[4]考虑故障的随机性和模糊性，利用模糊数学理论，建立了多种指标的隶属函数。文献[6]建立了变压器评估的正态云模型，通过期望、熵和超熵描述状态的不确定性，有效地实现了定性和定量之间地转换。文献[7]通过核函数将故障样本的特征转换为高维度的空间向量，放大了故障的有用特征，使聚类分析的准确性得到提高。

基于油中气体分析的IEC三比值法因其自身的特点，目前仍然有很高的实用价值。这里采用模糊聚类算法，将三比值法的编码模糊化，使故障特征值根据其数据特征自行分类，有效地克服了三比值法编码固化等问题。为了防止先验知识对故障分类数造成的误差，利用相关矩阵的定义和圆盘定理进行特征值分析，得到最佳分类数。采用人群搜索算法对初始参数进行优化，有效地避免了早熟现象，并提高了聚类的有效性和鲁棒性。

1 模糊聚类理论

聚类分析是一种无监督学习的多元统计分析方法，目的是客观地划分样本的类别，使得具有类似特征的样本划分到同一类，而具有不同特征的样本划分到不同类[9]。模糊聚类在聚类分析的基础上引入了隶属度的概念，用来描述样本对类别的模糊性。模糊c均值算法(fuzzy c-means，FCM)是一种基于目标函数的聚类算法，分类数需要事先给出，然后通过聚类中心和隶属度的迭代得出样本的最优分类[10]。由于其算法原理清晰且收敛速度较快，FCM算法广泛应用于各个领域。

对于n个不同的样本X={xi}，根据先验知识得出最佳分类数为c，FCM算法通过计算类内加权误差平方和作为目标函数[11]：

(1)

式中：U为隶属度矩阵；uij为模糊隶属度；V为聚类中心矩阵；m为模糊控制指数，一般取1.5～2.5，数值越小，模糊程度越低；dij为聚类中心的欧式距离。

为了求取目标函数的极值，FCM算法利用拉格朗日乘子法计算得到隶属度和聚类中心的迭代公式分别为

(2)

(3)

FCM算法的基本步骤如下[12]：

1)设定样本初始参数，包括分类数c、模糊控制指数m以及迭代终止阈值ε和迭代终止最大次数T；

2)确定初始的聚类中心V，并用公式(2)计算得到初始隶属度U；

3)利用式(1)计算目标函数值，如小于给定阈值ε则算法结束，否则利用式(3)和式(2)再次迭代，直到达到迭代终止条件。

从FCM的实现步骤可以看出，FCM的聚类结果严重依赖于分类数c，其值过大或者过小都将使聚类结果产生很大误差；FCM的初始聚类中心是随机确定的，最佳聚类中心会随之发生变化，这就给聚类分析带来了不确定性[13]；FCM采用欧氏距离方法聚类，每个样本都是等趋势划分，样本中的噪声也根据其聚类赋隶属度，这显然是不合理的。下面基于以上分析，对FCM算法进行了优化。

2 矩阵特征值分析

在变压器故障诊断中，故障的类别一般是根据专家经验来进行估计。这种方法缺乏客观的理论支撑，难以得出最佳的分类结果。随着大数据时代的来临，通过聚类有效性评估确定最佳分类数成为了研究的热点[14]。在文献[15]中，证明了可能性划分系数能有效地判定聚类的有效性，当可能性系数取得最大值时，聚类效果为最佳。文献[16]将聚类隶属度与样本的几何分布结合起来，依据类内紧密、类间分离的原则进行聚类有效性分析。文献[17]提出指标不受数据集形状的约束，利用离散距离来评估聚类效果。但是这些指标都必须经过反复迭代，遍历所有可能的分类数，才能确定最佳聚类结果，因此极其耗费时间，导致现有的评价标准无法应用在大多数工程项目中。文献[18]提出了基于矩阵特征值分析的有效性指标，克服了其他有效性指标的低效性，而且得到最优分类的正确率不会降低。变压器的故障分析属于多维度、分类数不确定的复杂聚类分析，鉴于矩阵特征值分析的独特优势，故采取该方法得出最佳的聚类数。

根据相关矩阵[18]的定义及其特征值可知，特征根的大小反映了同一类样本的相似程度。根据Gerchgorin圆盘定理[19]，如果实际的最佳分类数是c个，则其L个特征值出现的情况为

λ1≥λ2≥…λc≥λc+1≈…≈λL

(4)

式中，λ1到λc是c个相对较大的特征根。

最优的分类数由于其特征根的不同，可以得到明显不同的圆盘。按照圆盘定理，可以定义指标的最优分类数如下，即：

(5)

式中，c是在闭集合[1,L-1]内可能取得的分类数，当第1个非负的GDE(c)值出现时所对应的c，即为最优的分类数。

3 聚类模型的参数优化

在FCM中，聚类的有效性对初始聚类中心有很大的依赖性。为了得到最优结果，可以选定不同的初始聚类中心启动该算法，通过比较不同的聚类结果，得出最优解。文献[20]利用粒子群算法(particle swarm optimization，PSO),对数据集进行全局搜索，能够弥补FCM对初始聚类中心敏感的缺陷，但是易出现早熟现象，以致于不能全局寻优。文献[21]提出用改进的遗传算法(genetic algorithm，GA)来自动选取保持全局特性的聚类中心点，再利用欧式距离的判别方法进行其他点的判断。文献[22]将粒子群算法和遗传算法结合起来，充分利用GA的随机搜索能力和PSO的局部细致搜索能力。另外，还有一些智能算法及其混合算法应用在变压器故障诊断中。虽然在一定程度上改善了聚类的结果，但是当面对复杂多维优化问题时，由于其目标函数存在着数目众多的局部极值，导致聚类时很容易发生早熟和收敛速度慢等现象。

所采用的人群搜索算法(seeker optimization algorithm, SOA), 是一种新型的智能搜索算法[23]，具有更好的鲁棒性与较快的收敛性，算法的求解过程避免了早熟现象的发生，对于工程领域的复杂优化问题具有收敛精度高等特点。

3.1 人群搜索算法

SOA算法根据人的思维过程，在解空间对函数进行寻优[23]。在优化过程中，其搜寻过程可理解为在可能的解空间里，最优解的位置趋向于较优解的附近。因此，在较优的位置应该进行细致的搜索，而对于较差的位置，应该再扩大搜索范围[24]。

3.1.1 搜索步长

SOA算法用模糊系统逼近来表征搜索的不确定性，建立目标函数和步长之间的联系。搜索步长模糊变量表示如式(6)。

(6)

式中：x为输入样本；uA为隶属度；δ、μ为隶属函数参数。

隶属度与函数值排列顺序成正比，如式(7)所示。

uij=rand(ui,1)(j=1,2,…D)

(7)

式中：D为搜索空间的维度；uij为j维搜索空间第i个特征量的隶属度；函数rand表征了搜索的随机性。

搜索步长定义为

(8)

式中：αij为第j维的搜索步长；δij为高斯隶属函数参数，其值由式(9)和式(10)确定。

(9)

(10)

式中：xmin和xmax为最小和最大目标函数的位置；ω为权值；t和tmax为当前的迭代次数和最大迭代次数。

3.1.2 搜索方向

通过人的行为分析得到第i个位置的利己方向、利他方向以及预动方向，如式(11)至式(13)所示。

(11)

(12)

(13)

通过几何平均来确定最终搜索方向，如式(14)。

(14)

式中：φ1和φ2为[0,1]内的常数；ω是惯性权重。

3.1.3 人群搜索算法的实现

步骤1：基本参数设置。根据实际问题，设置搜寻速度、进化代数及种群规模。

步骤2：随机设置人群搜索的开始位置。

步骤3：初始化目标函数值，并得出最优值。

步骤4：确定搜寻策略。确定步长和方向。

步骤5：位置更新。更新公式为

Δxij(t+1)=αij(t)dij(t)

(15)

xij(t+1)=xij(t)+Δxij(t+1)

(16)

步骤6：完成一次迭代，t=t+1。

步骤7：若达到终止条件，则认定为最佳位置，否则，转至步骤3继续迭代。

4 建模过程

4.1 变压器特征量的选取

变压器油中溶解气体包含了运行设备的故障信息，并且测量技术比较完善，是一种成熟有效的状态评估指标[25]。

如果变压器内部发生故障，温度会显著升高，进而加速绝缘材料分解[26]。当电力变压器发生不同类型的故障时，其产生的特征气体含量会有所不同，但发生相同故障时产生的特征气体会有某种相似性。利用变压器故障特征气体的聚集效应可以生成聚类中心，并通过其分布情况给出隶属度，从而实现故障的分类。

4.2 建模流程

对电力变压器故障样本进行矩阵特征值分析，求取相关矩阵及其特征值，得出最优分类数。同时为提高故障诊断精度，对FCM算法的初始聚类中心用SOA进行优化。建模流程如图1所示。

5 算例分析

收集了230组故障明确的变压器故障数据，挑选其中80组作为训练聚类中心，用文献[27]给出的40组作为测试数据。为了得到更好的聚类中心，训练集各故障状态均匀分布，具体个数如表1所示。

对所收集的故障样本求取相关矩阵和特征值，进行矩阵特征值分析，第1个非负的GDE(c)值出现的时候，c的值为6,故最优的分类数为6类，与实际情况相符。

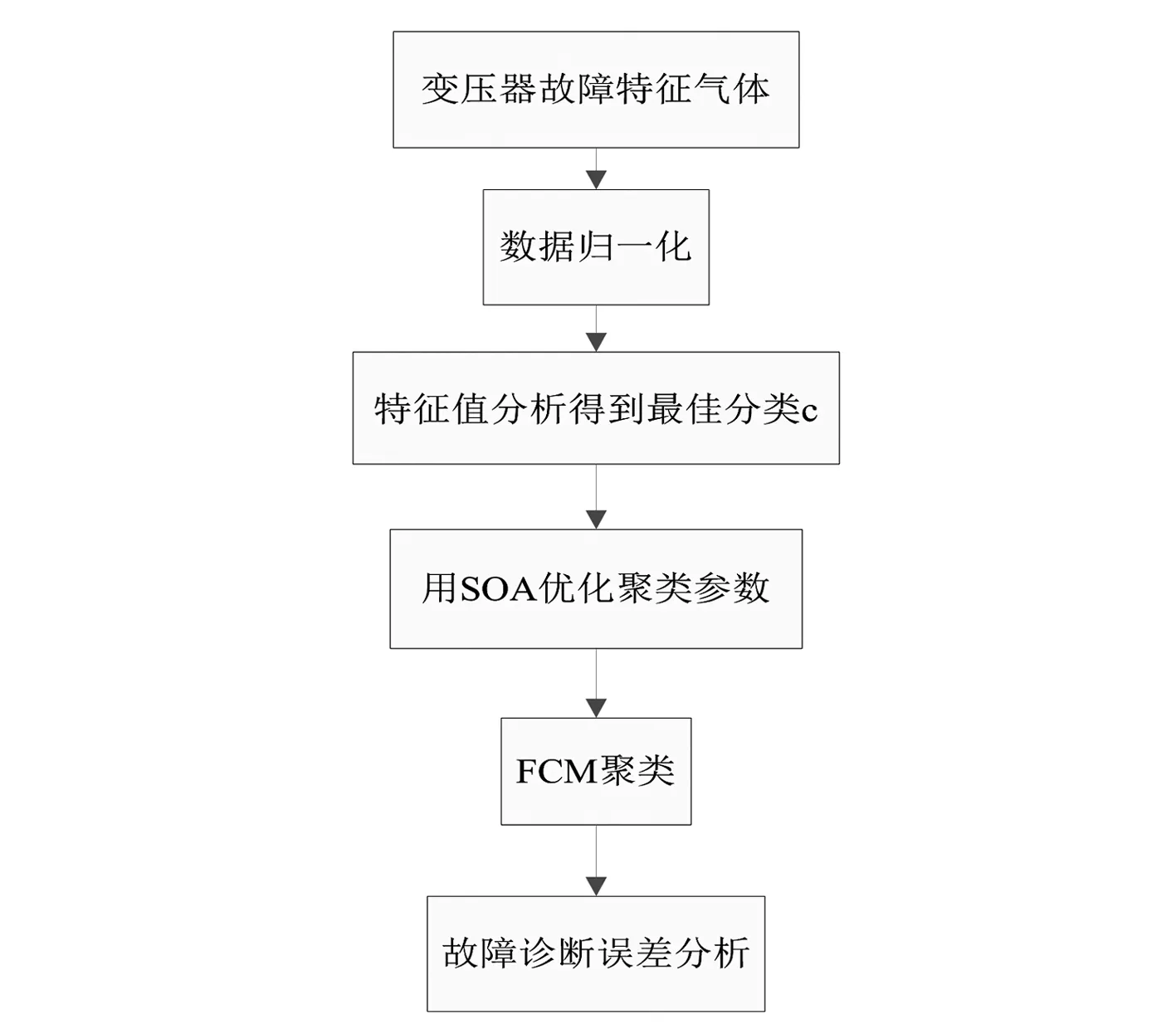
图1 变压器故障诊断模型结构表1 变压器故障样本

故障类型训练集测试集无故障154低能放电159高能放电156低温过热155中温过热158高温过热158总计8040

从收集的数据集可以看出，原始数据具有不同的数量级，为了使较小数量级的数据不被忽略，有必要对数据进行归一化处理。

(17)

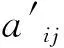
SOA优化算法的初始参数设定为：进化代数为100，种群规模为20，算法的最大隶属度Umax=0.95，最小隶属度Umin=0.01，权重最大值ωmax=0.9，权重最小值ωmin=0.1，模糊控制系数m=2。将训练样本中的数据利用SOA算法计算后得出各故障的最优聚类中心，如表2所示。适应度曲线如图2所示。

表2 SOA最优聚类中心

图2 SOA适应度曲线

测试集中的数据对应的故障类型如下：1—5为低温过热，6—13为中温过热，14—21为高温过热，22—30为低能放电，31—36为高能放电，37—40为正常。

文献[27]利用PSO算法进行优化，得出聚类中心如表3所示，测试结果除了35无法确定结果，38得出错误结果外，其他的全部正确，正确率达到95%。而利用所提出的SOA进行优化，得出的结果除了2号错误，其他的全部正确，正确率为97.5%，高于改进的PSO算法，这是由于SOA算法对于数据的全局搜索能力要强于PSO算法，并能够有效地避免陷入局部最优值，从而得出更优的聚类中心。两种方法得出的部分最高隶属度如表4所示。

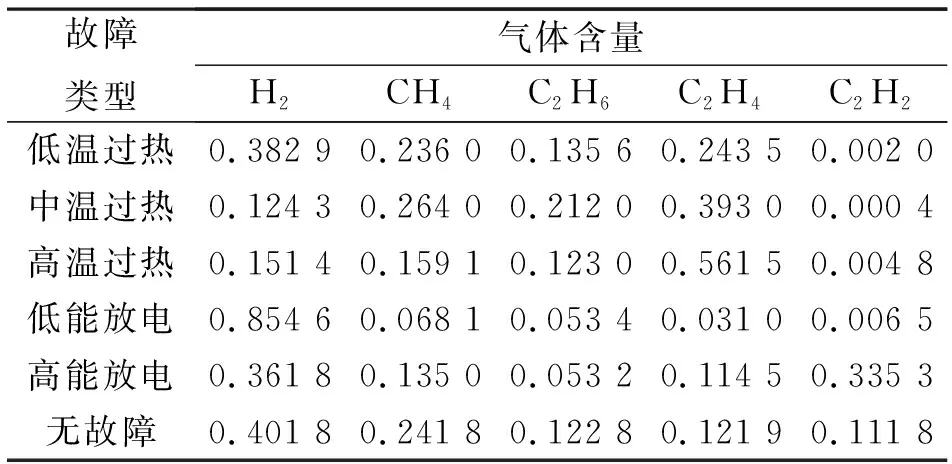
表3 PSO最优聚类中心

从两种方法的隶属度矩阵和表4所列部分结果可以看出，所用方法在保证正确率的情况下，聚类效果有了显著提高，这是因为SOA算法充分考虑了搜索的随机性和模糊性，在全局性和局部性搜索性能上均优于传统的PSO算法。

6 结 语

对变压器状态检修过程中状态分类和故障诊断优化进行了研究，得出如下结论：

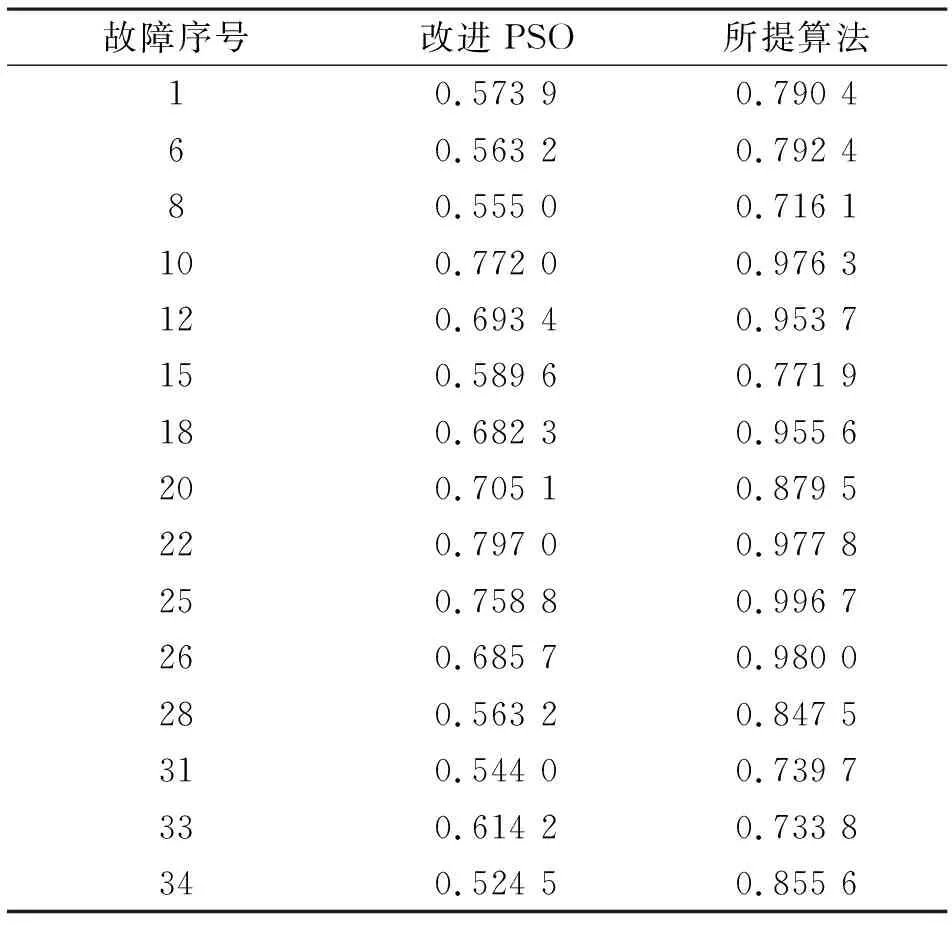
表4 两种方法故障诊断结果对比

1)提出了用圆盘定理和矩阵特征值分析确定状态的最优分类数，克服了主观因素的影响，极大地提高了故障诊断的稳定性；

2)通过模糊聚类理论，将变压器状态边界模糊化，反映了故障诊断的不确定性；

3)针对模糊聚类对初始值敏感的问题，提出用SOA算法进行优化，建立了SOA-FCM模型，改善了聚类的效果，提高了故障诊断的准确性。

通过仿真实验，验证了所提方法的有效性。

[1] 杨廷方, 刘沛, 李景禄, 等. FCM结合IEC三比值法诊断变压器故障[J]. 高电压技术, 2007, 33(8):66-71.

[2] 许惠君, 王宗耀, 苏浩益. 基于DGA的反馈云熵模型电力变压器故障诊断方法研究[J]. 电力系统保护与控制, 2013, 41(23):115-119.

[3] 公茂法, 张言攀, 柳岩妮, 等. 基于BP网络算法优化模糊Petri网的电力变压器故障诊断[J]. 电力系统保护与控制, 2015, 43(3):113-117.

[4] 廖瑞金, 王谦, 骆思佳, 等. 基于模糊综合评判的电力变压器运行状态评估模型[J]. 电力系统自动化, 2008, 32(3):70-75.

[5] 张晶晶, 许修乐, 丁明,等. 基于模糊层次分析法的变压器状态评估[J]. 电力系统保护与控制, 2017, 45(3):75-81.

[6] 张镱议, 廖瑞金, 杨丽君, 等. 基于云理论的电力变压器绝缘状态评估方法[J]. 电工技术学报, 2012, 27(5):13-20.

[7] 熊浩, 孙才新, 廖瑞金, 等. 基于核可能性聚类算法和油中溶解气体分析的电力变压器故障诊断研究[J]. 中国电机工程学报, 2005, 25(20):162-166.

[8] 董明, 孟源源, 徐长响,等. 基于支持向量机及油中溶解气体分析的大型电力变压器故障诊断模型研究[J]. 中国电机工程学报, 2003, 23(7):88-92.

[9] 黄卫春, 刘建林, 熊李艳. 基于样本-特征值加权的可能性模糊核聚类算法[J]. 计算机工程与科学, 2014, 36(1):169-176.

[10] 宋志杰, 王健. 模糊聚类和LM算法改进BP神经网络的变压器故障诊断[J]. 高压电器, 2013, 49(5):54-59.

[11] 李俭, 孙才新, 陈伟根,等. 灰色聚类与模糊聚类集成诊断变压器内部故障的方法研究[J]. 中国电机工程学报, 2003, 23(2):112-115.

[12] 陈灿. 基于粒子群算法的模糊聚类研究[D]. 桂林：广西师范大学, 2005.

[13] 李超顺, 周建中, 安学利,等. 基于加权模糊核聚类的发电机组振动故障诊断[J]. 中国电机工程学报, 2008, 28(35): 79-83.

[14] 周开乐, 杨善林, 丁帅,等. 聚类有效性研究综述[J]. 系统工程理论与实践, 2014, 34(9):2417-2431.

[15] 范九伦, 吴成茂. 可能性划分系数和模糊变差相结合的聚类有效性函数[J]. 电子与信息学报, 2002, 24(8):1017-1021.

[16] Xie X L, Beni G. A Validity Measure for Fuzzy Clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(8): 841-847.

[17] Yue Shihong, Wang J, Wu T, et al. A New Separation Measure for Improving the Effectiveness of Validity Indices[J]. Information Science, 2010, 180(5): 411-423.

[18] 岳士弘, 黄媞, 王鹏龙. 基于矩阵特征值分析的模糊聚类有效性指标[J]. 天津大学学报, 2014,47(8)：689-696.

[19] Watking D S. Fundamentals of Matrix Computation

[M]. USA: John Wiley & Sons, 2002.

[20] 马叶芝, 焦彦军, 王东升, 等. 变压器故障诊断中溶解气体的PSO-WFCM算法研究[J]. 高压电器, 2014,50(1)：72-76.

[21] 田质广, 张慧芬. 基于遗传聚类算法的油中气体溶解气体分析电力变压器故障诊断[J]. 电力自动化设备, 2008,28(2)：15-18.

[22] 雷浩辖, 刘念, 崔东军, 等. 基于GA与PSO混合优化FCM聚类的变压器故障诊断[J]. 电力系统保护与控制, 2011, 39(22):52-56.

[23] 董慧康. 基于人群搜索-支持向量机的心脏病多生理参数诊断方法研究[D]. 天津：河北工业大学, 2014.

[24] 魏立兵, 赵峰, 王思华. 基于人群搜索算法优化参数额支持向量机短期电力负荷预测[J]. 电测与仪表, 2016, 53(8): 45-49.

[25] 周健, 黄昕, 邹剑, 等. 变压器油中溶解气体故障诊断的改进模糊算法[J]. 广东电力, 2015, 28(3): 86-91.

[26] 孙才新, 郭俊峰, 廖瑞金, 等. 变压器油中溶解气体分析中的模糊模式多层聚类故障诊断方法的研究[J]. 中国电机工程学报, 2001, 21(2):37-41.

[27] 韩富春, 廉建鑫, 高文军, 等. 改进PSO与模糊聚类相结合的变压器故障诊断[J]. 电气技术, 2011, 5(2):1-4.