NONLINEAR OCEAN INTERNAL WAVES∗†
2018-07-06BolingGuo
Boling Guo
(Institute of Applied Physics and Computational Math.,P.O.Box 8009,Beijing,100088,PR China)
Yitong Pei‡
(The Graduate School of China Academy of Engineering Physics,P.O.Box 2101,Beijing,100088,PR China)
1 Introduction
Besides the sea level fluctuation,the fluctuation phenomenon also occurs in the ocean,called ocean internal waves.It is a fluctuation of structural stability occurs in the density layer of seawater.The amplitude of ocean internal waves reaches its maximum below the sea level.
Internal wave is an important form of seawater motion the same as the surface wave in the ocean.It transmits energy from large-and meso-scale motion to smallscale motion,which leads to the internal mixing of seawater.Also it carries the deep and cold water along with its nutrients to the upper layer of the ocean,which is good for the growth of marine organisms.The wave of isodense surface caused by internal wave will affect the magnitude and direction of sound velocity in the ocean,thus affect the effectiveness of sonar,and play a beneficial or harmful role in submarine concealment and monitoring.The ups and downs of isodense surface of the ocean will make the underwater submarine navigate and stay up and down.In particular,nonlinear internal waves have great energy.They interact with other objects and have their own nonlinear effects,which can destroy ships,submarines and aircraft carriers to a great extent.Therefore,the research on it is not only of academic significance,but also of great practical and military significance.

1.1 Interfacial waves
Internal waves in the ocean have many properties that surface waves don’t have.Interfacial waves is one of the simplest forms of internal waves called interfacial waves,which occur at the interface of two layers of seawater with different densities.The density in the realocean varies continuously.The waves among the strong spring layers in the ocean can be regarded as interfacial waves so that we can explain lots of internal wave phenomena
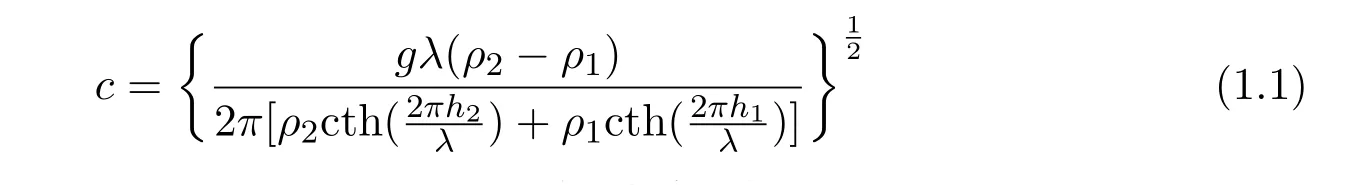
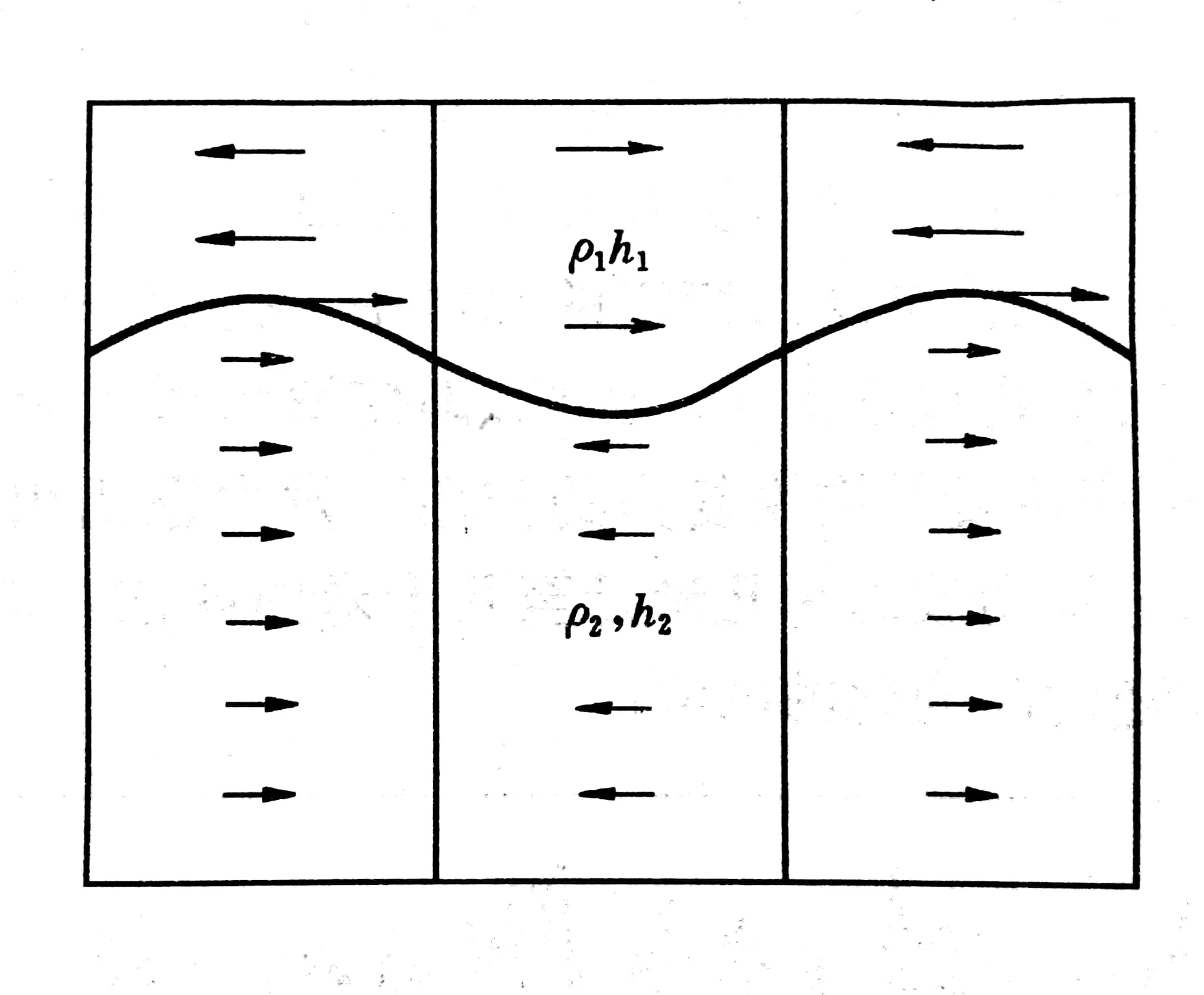
Figure 1.1:Interfacial waves
(1)The interfacial shortwaves
When the interface is in the middle of an ocean of infinite depth,we haveλ?h1,h2.From(1.1),we obtain

(2)The interfacial long waves
Whenλ?h1,h2,from(1.1),we obtain

where=(ρ2+ρ1)/2.Thus the formula of interfacial wave contains coefficients of[(ρ2−ρ1)/(ρ2+ρ1)]1/2,which is different from that of surface wave.There is a small density contrast between the two layers in the oceans,so the coefficient is also very small.It can be seen that the velocity ratio of the interface wave to the surface wave with the same wavelength is about 1/20.That is,the velocity of the interfacial wave is much slower than that of the surface wave.
(3)The amplitude of interfacial waves
The amplitude of sine surface wave isa,which has energy within a wavelength as follows:
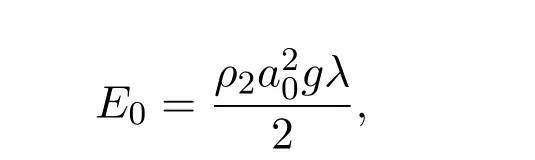
and the energy of the internal wave at the corresponding interface isE=(ρ2−ρ1)a2gλ/2.If we compare the interfacial waves with the surface waves with equal energy,E=E0,we have
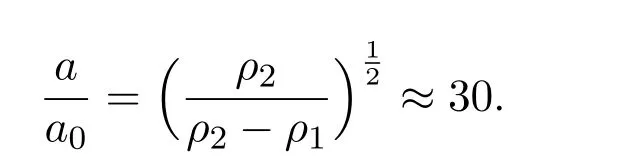
Therefore if the surface wave and the interface wave are excited with the same energy,the amplitude of the interfacial wave is about 30 times that of the surface wave.In ocean surveys,internal waves with a height of several tens of meters can often be recorded.
(4)The water particle of interfacial waves
The interfacial wave causes horizontal movement in opposite direction between the upper and lower layers of seawater,resulting in a strong shear velocity at the interface.Due to the opposite flow direction between the peak and the trough in the same layer,the radial convergence and divergence of the water particle are caused.The divergence area is formed after the valley before the peak,and the radiative area is formed after the peak of the valley,as shown in the following figure:

Figure 1.2:Water particle of interfacial waves
1.2 The internal waves with density varying continuously in the ocean
(1)The restoring force of internal wave
The restoring force of surface wave is mainly gravity,so it is called surface gravity wave.The recovery force of internal wave is Coriolis force and weakening gravity(that is,the difference between gravity and buoyancy).Because of its weak restoring force,its motion is much slower than that of surface wave,both its propagation speed and the movement of water particle are very slow.
(2)The frequency of internal wave
The frequencyσof the internal wave is between the inertial frequency

and the Brünt-Väisälä frequency

that is

wherec0is the speed of sound.The Brünt-Väisälä frequencyNrefers to the frequency of free oscillations in the vertical direction of Seawater micromass after being disturbed by a certain force in a stable density stratification stable ocean.It depends on the vertical gradient of seawater density dρ/dz.
(3)The propagation direction of internal wave
The propagation direction of internal wave is not horizontal.It generally propagates at an angleαin the horizontal direction.Angleαis a function of internal wave frequencyσ,that is,

which can be seen from the upper form that when the internal wave frequency is higher,the angleαbecomes smaller.And the propagation direction is close to horizontal direction.On the other hand,the propagation direction is steeper when the frequency is lower.Therefore,the propagation direction of internal waves changes with different frequencies.
(4)The energy transport of internal wave
The energy is transported by group velocity,where the group velocity of internal wave is equal to the wave velocity,and its direction is vertical to the wave velocity,both of which are in the same vertical plane.So a strange phenomenon is that when the waveform syncline propagates in the upper(lower)direction,the wave energy is transported lower(upper).
In the process of internal wave energy transmission,reflection will occur if the sea surface or sea floor is encountered.The angle between wave velocity and horizontal direction is equal to that between group velocity and vertical direction.The angle between the incident energy beam and the vertical direction equals that between the reflection energy beam and the vertical direction.This is different from the reflection that the light encounters with the interface.If the incident energy beam points to the lower(upper)side of the slope,the reflected energy beam refers to the upper(lower)side of the syncline,as shown in Figure 1.3.

Figure 1.3:The propagation and reflection of internal wave
(5)The superposition of internal waves
On the steeper sea floor,the incident and reflected internal waves may form standing waves in the vertical direction.The standing wave has wave loop.Based on different stratification conditions and reflection conditions in the ocean,the internal waves may take the form of an obvious energy beam(called ray)or model form.
At present,the research on the formation Mechanism of internal wave is still under discussion.There are many factors that can excite internalwaves,which may come from the sea,the sea floor,and the interior of the sea,such as sea surface wind stress,sea level pressure field,the uneven horizontal distribution of sea water density in the upper mixed layer,tidal current or current flowing through the scraggy seafloor,the existence of flow shear inside the seawater and so on.The study of dissipation mechanism of its energy is not in-depth.However,it has been revealed that internal wave breakage can transfer energy to small scale turbulence,the average shear flow may absorb the energy of the internal wave,and the friction between seawater and the boundary will consume the energy of the internal wave.
Both the generation and dissipation of internal waves and the physical properties of seawater passing through the propagation process have strong randomness.Therefore,it is necessary to record the time series and spatial series data of temperature,salinity,velocity and flow direction of sea water in the investigation of internal wave.The statistical and dynamic characteristics of ocean internal waves can be obtained by using Random Process Theory.
The study of nonlinear ocean internal waves has been carried out since 1960.In 1965,Perry and Schimke discovered 80 meters high and 2,000 meters long internal waves in the Andaman Sea.In 1982,Fu and Holt observed multiple internal waves in Gulf of California.In 1998,Stanton and Ostrovsky discovered an Internal wave of 147 meters high.In 2004,Duda found an amplitude of 150 meters in the South China Sea.At the same time,the numerical calculation of the Euler equation with the boundary conditions of the ocean finite region was carried out by G.Lamb.In theory,Grimshaw and Ostrovsky simplified these problems into variable coefficient Kdv equation,KP equation and BO equation,and obtained the blowup image of nonlinear ocean internal wave.We will give a brief introduction based on the different models.
2 The Model and Calculation of the Wave Rupture Formed by Internal Soliton Waves Impacting the Sloped
Consider the following numerical models:
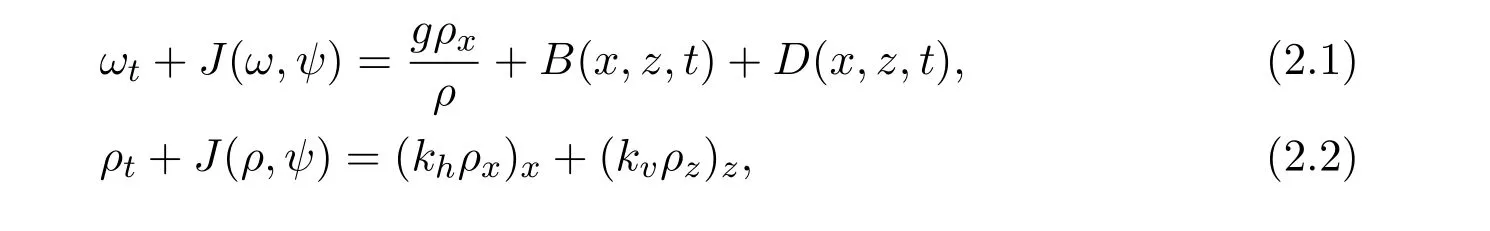
whereρis the density of water,kv,khare the vertical and horizontal turbulence coefficients respectively,J(a,b)=ax bz−az bx,ψ(x,z,t)is the stream function,ω(x,z,t)is the vorticity,u=ψz,w=−ψx,ω=ψxx+ψz z.

whereab,kbare dissipation constants,ao,α,pare parameters,Nis the Local BV frequency withN2(x,z,t)=−gρz/ρ,and the horizontal viscosityahand the turbulent diffusionkhare parameters with
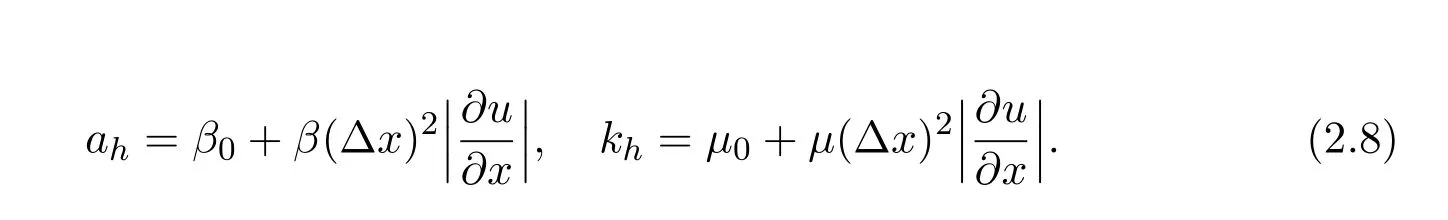
Equations(2.1)-(2.2)are considered under boundary conditions:

wherenis the exterior normal.The image of the internal wave impact slope is shown below:
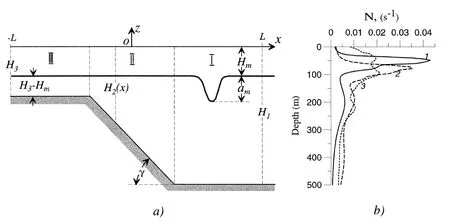
Figure 2.1:The diagram of Computing area
The image of internal wave rupture can be obtained from the calculated results.Figure 2.2 shows the breaking of internal wave.Figure 2.3 shows the evolution of density(upper),horizontal velocity(middle)and vertical velocity(bottom)during internal solitary wave rupture.Figure 2.4 describes the evolution of density field in the process of internal wave breaking.Figure 2.5 shows the density,horizontal velocity and vertical velocity field of 1057 s after posterior wave surface rupture.

Figure 2.2
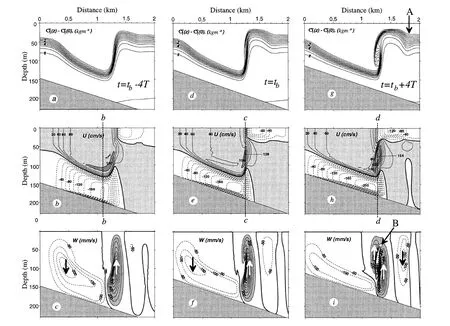
Figure 2.3

Figure 2.4
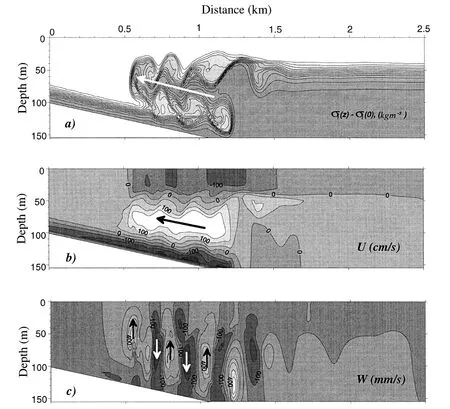
Figure 2.5
3 Motion of Strongly Nonlinear Internal Waves in Shallow and Deep Water
Consider the following strong nonlinear gravity waves with large amplitudes,which are two-layer shallow water wave equations with non-flat bottoms.
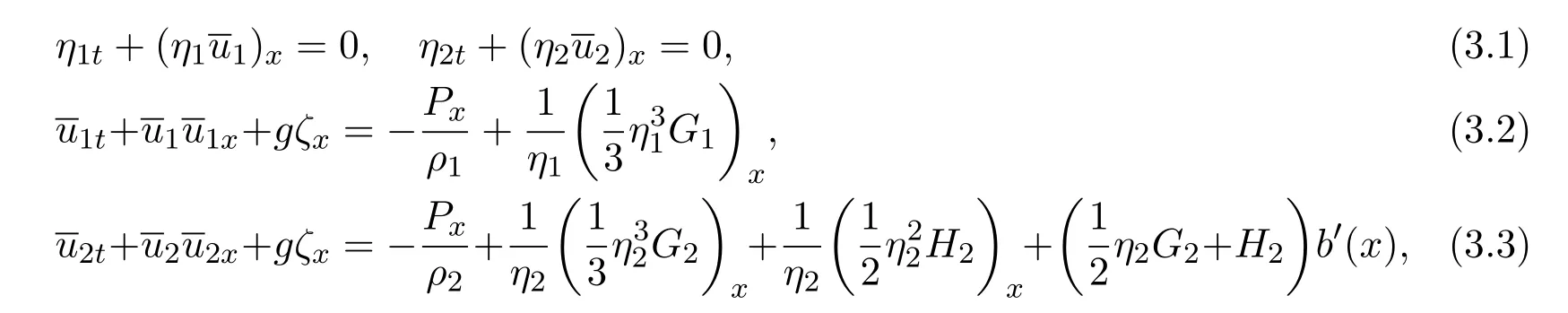
wheregis the acceleration of gravity,ρiis the fluid density,ηiis the layer thickness,is the average velocity in layer,the nonlinear dispersion termGiis defined as:
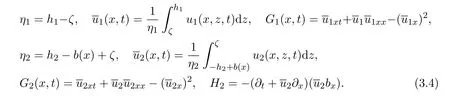
The two-layer flow graph is given in Figure 3.1.

Figure 3.1:Two-layer flow
3.1 Weakly nonlinear model
Letζ=O()=O()?1,then equations(3.1)-(3.3)can be simplified as weakly nonlinear models.Forζandu1we have
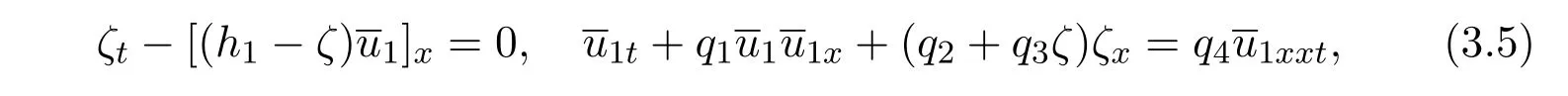
whereqiis the slowly varying function,
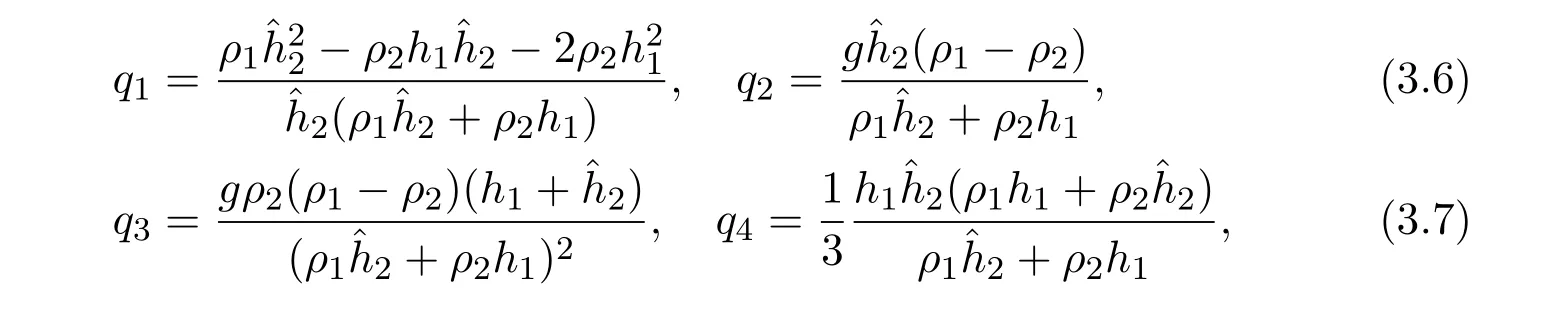
where=h2−b(x).
For unidirectional waves,b(x)=0,from(3.7)we obtain
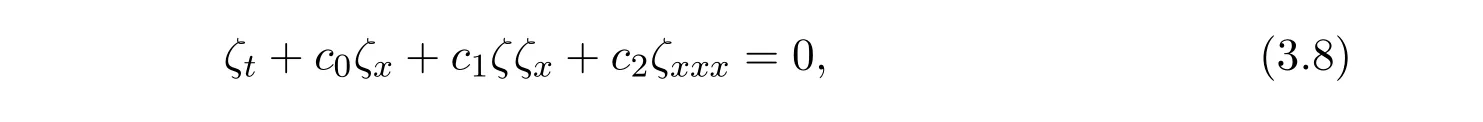
where
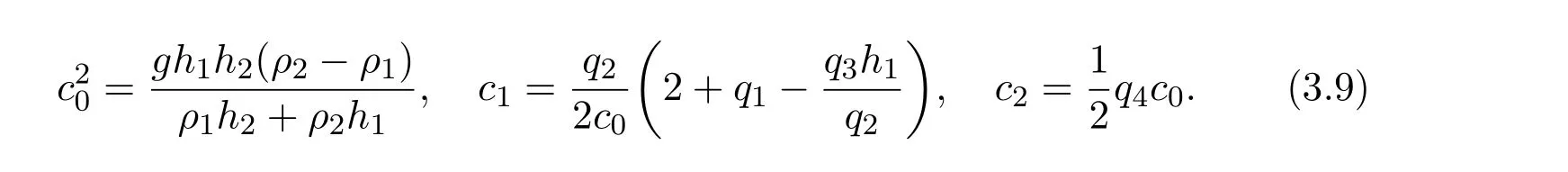
3.2 The solitary wave and its stability
Letcbe the velocity of solitary wave,then we have
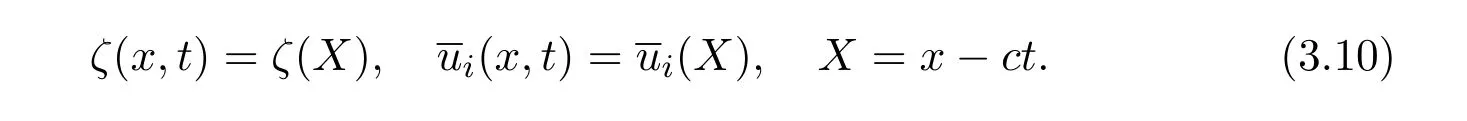
Lettingηi→hi,|x|→∞,from(3.1)we obtain
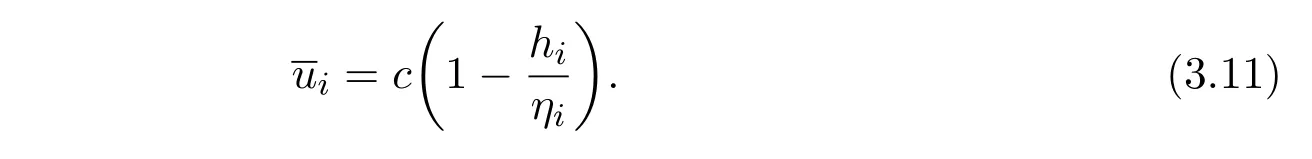
Letb(x)=0,so we have
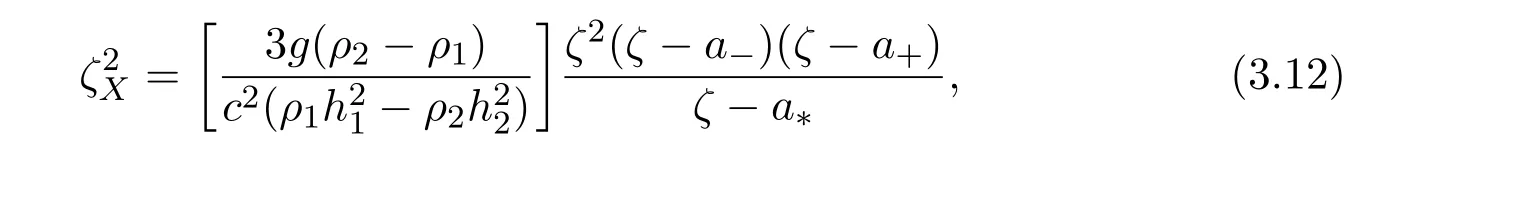
where
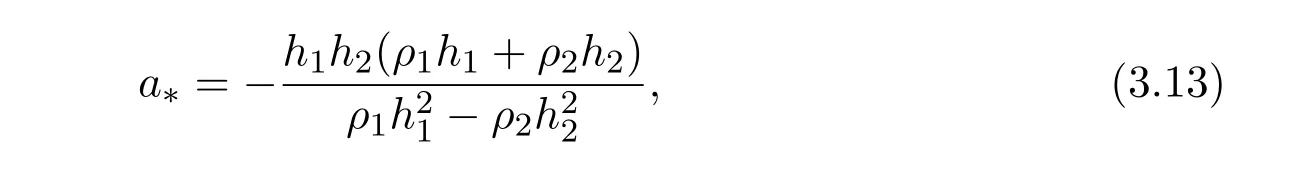
a±is the roots of the quadratic equation

with
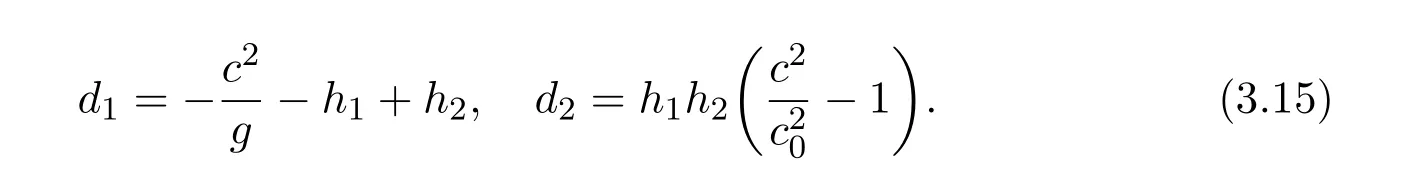
From this we can see thatζis bounded andis nonnegative.Solitary waves are elevated when(h2/h1)<(ρ2/ρ1)1/2,and are fallen when(h2/h1)>(ρ2/ρ1)1/2.Figure 3.2 shows the stability and instability of the solitary waves.Figures 3.3 and 3.4 means two solitary waves are chasing each other.Figure 3.5 means two solitary waves are colliding.
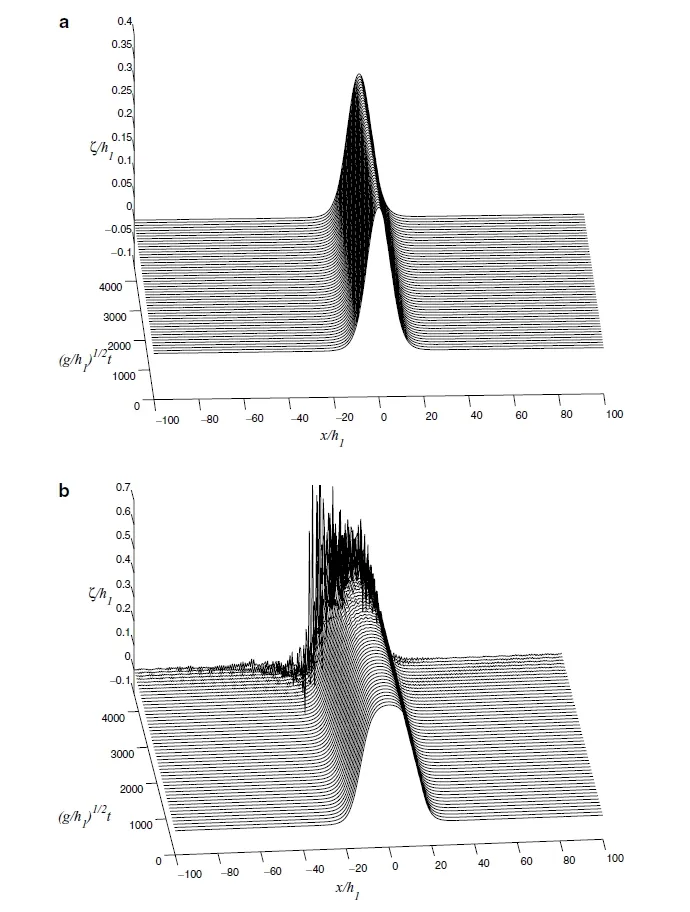
Figure 3.2
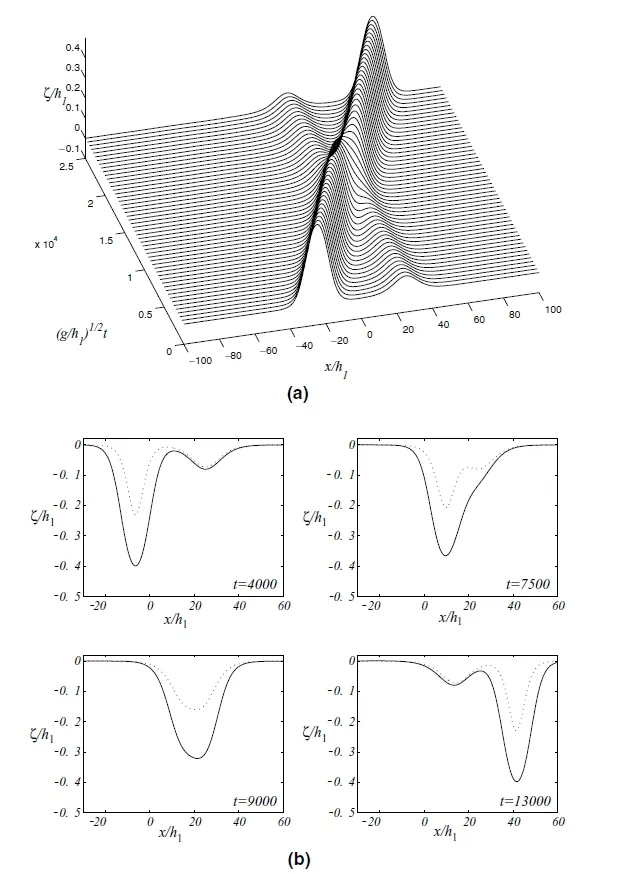
Figure 3.3
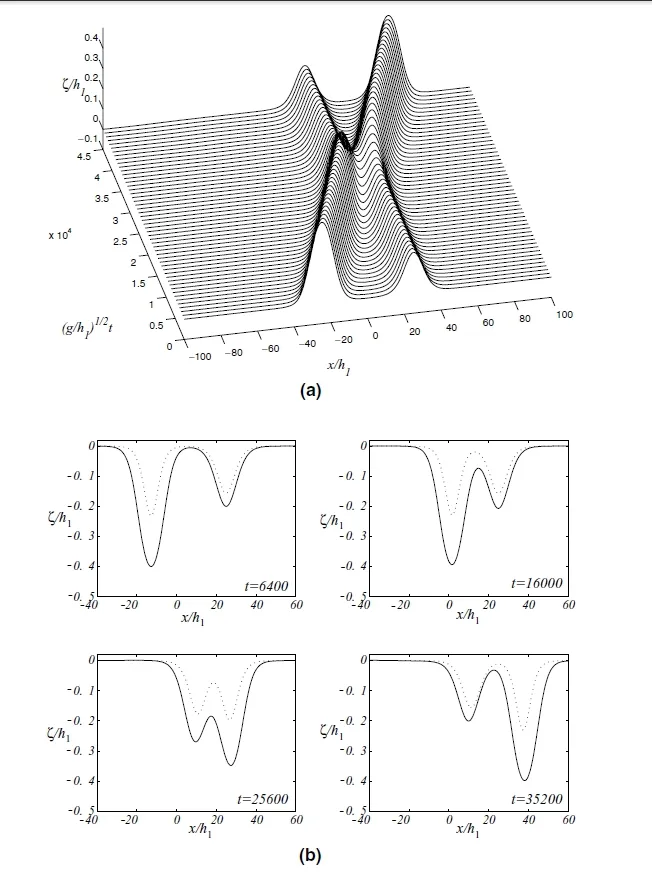
Figure 3.4
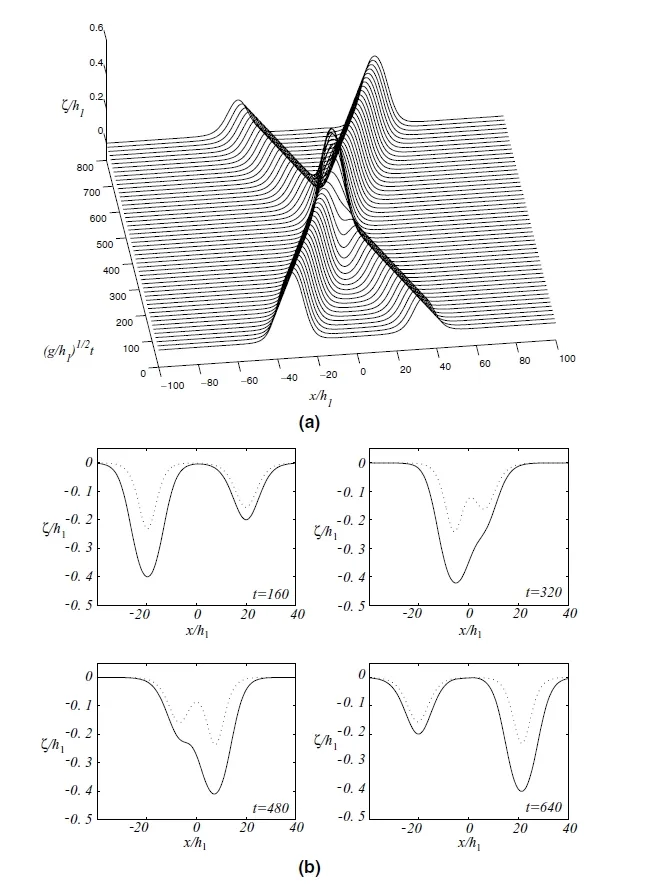
Figure 3.5
3.3 Solitary waves over inhomogeneous terrain
Let(x)=h2−b(x),then from(3.2)-(3.3)we obtain the Kdv equation
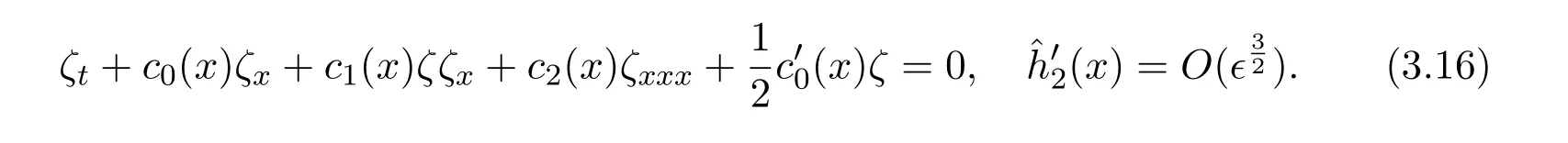
By the coordinate transformation we have
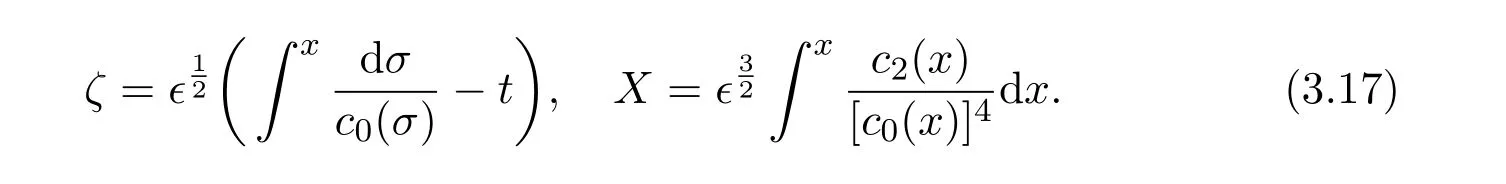
Letting

we obtain
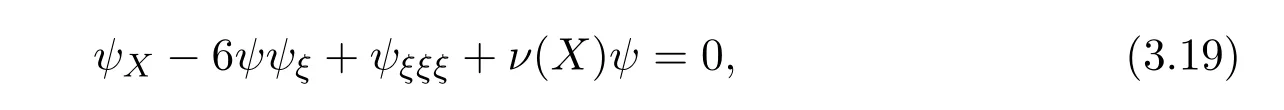
whereν(X)is a function dependent onh1,h2,,.Figures 3.6 and 3.7 are the topographic condition of the bottom of climbing slope.
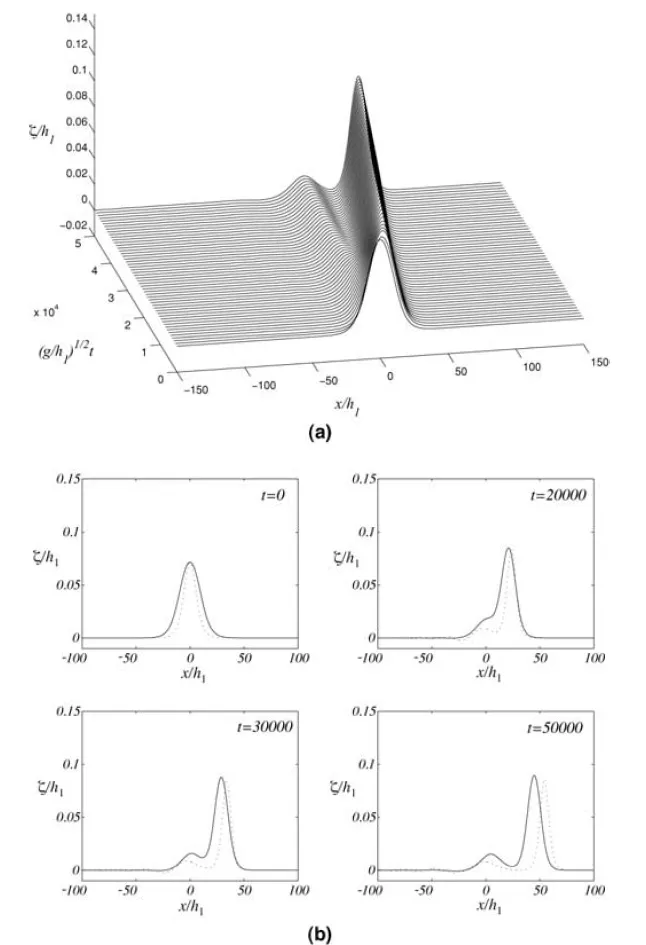
Figure 3.6

Figure 3.7
4 The model of deep water area
Consider the following model

where
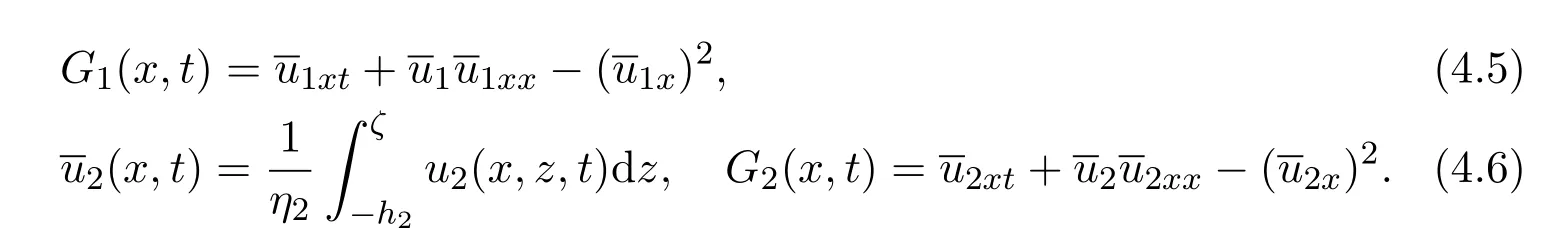
Let

From(4.1)-(4.3)we have
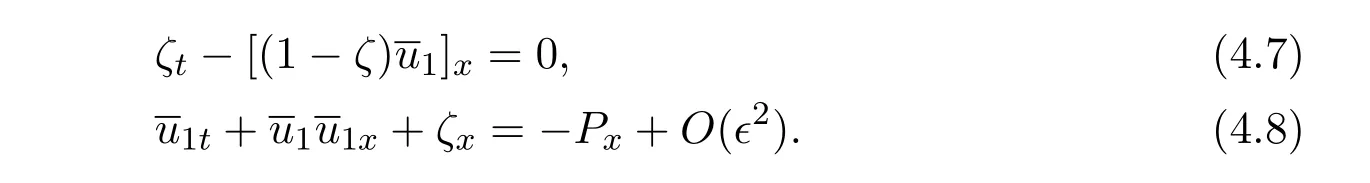
By making dimensionless transformations,we have

where(φx,φz)=(u2,w2),C(t)is an arbitrary function oft,and

withφx(x,?ζ,t)=φx(x,0,t)+O(?).We can easily have

and the velocity potentialφsatisfies the following boundary value problem:

From(4.17)we obtain

Let−h2≤z≤0,then we have
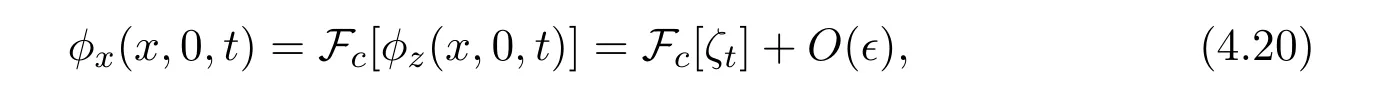
where
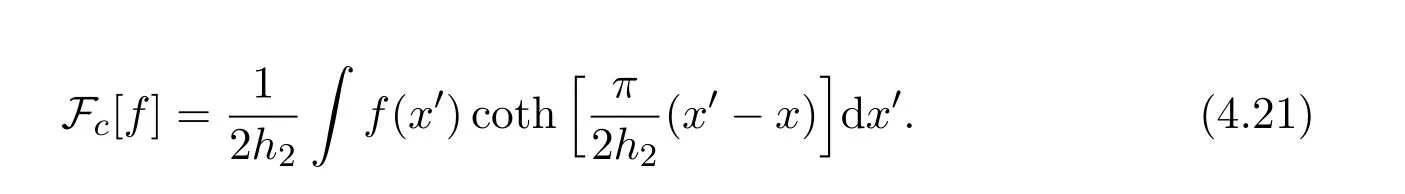
From(4.12)and(4.20),we obtain
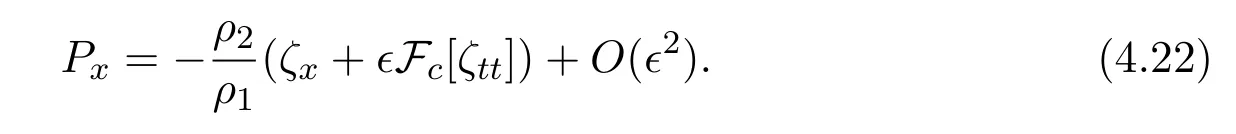
Then we have
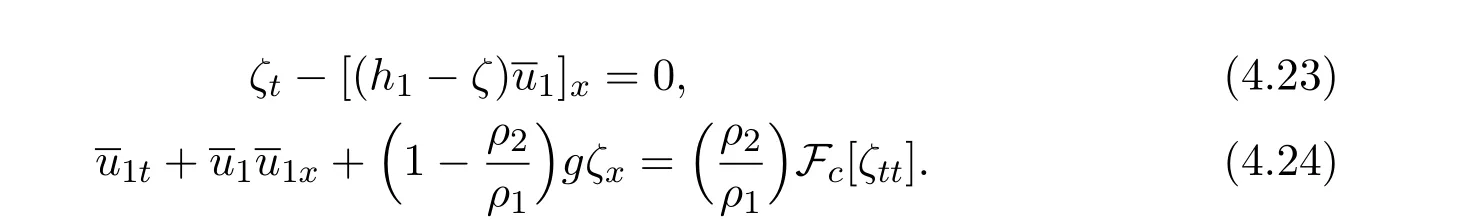
We obtain

whereη1=h1−ζ.From(4.23)-(4.25),it follows that
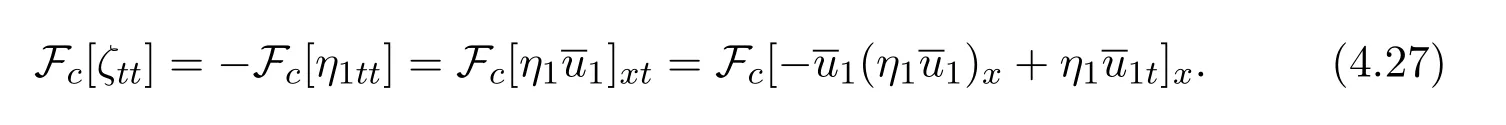
Lettingh2→∞,we have the transformFc→H
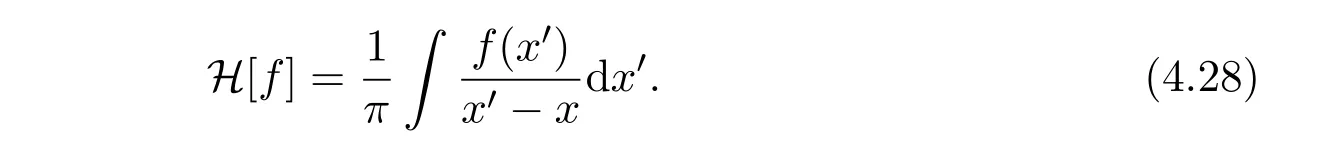
Equations(4.21)-(4.24)satisfying the following mass conservation,irrotationality,momentum conservation and energy conservation

Noticing the upper layer ofdeep water passes through the lower layer,fromg→−g,ζ→−ζ,we have
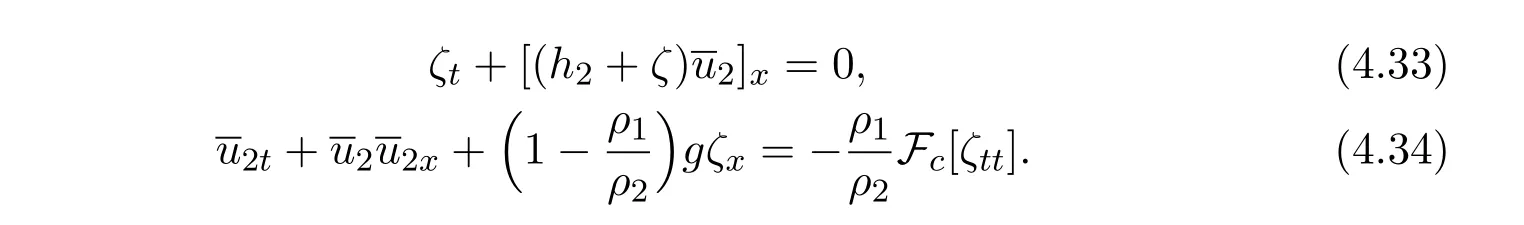
Under the condition of weak linearity,

we obtain weakly linear wave equations
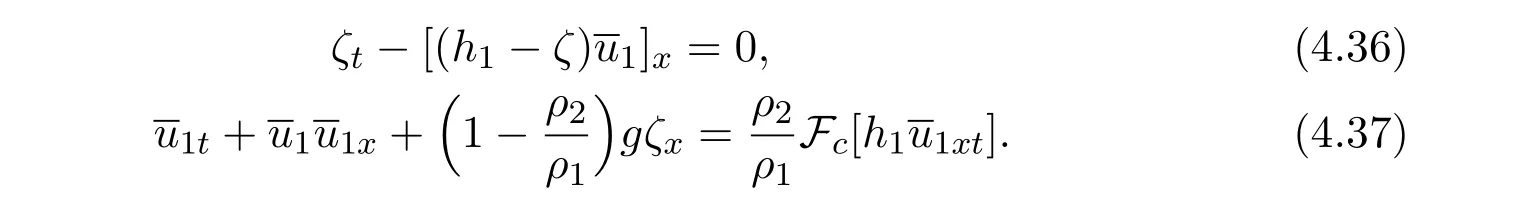
As for unidirectional wave,we obtain the ILW equation

where
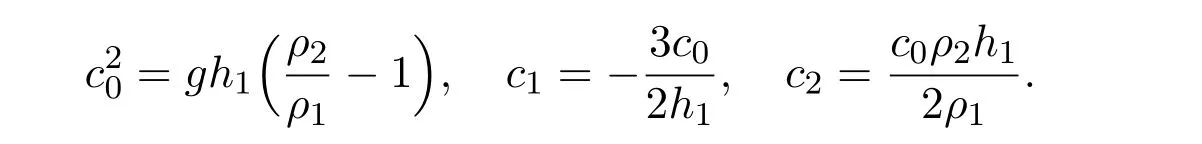
The solitary wave of equations(4.33)-(4.34)can be calculated easily.Figure 4.1 means numerical solution of solitary Wave Propagation atc/c0=1.2.Figure 4.2 means numerical solution of single solitary wave fission atc/c0=1.2 and(x,0)=0.Figure 4.3 means numerical solution of frontal collision of two identical solitary waves atc/c0=1.2,with the initial positionx=±100,which spread in the opposite direction.
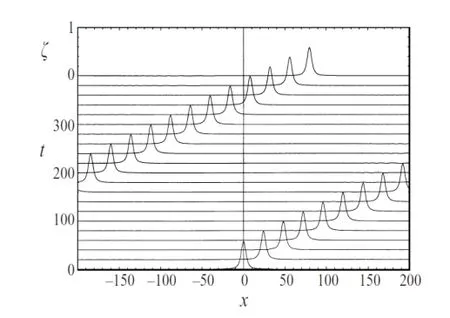
Figure 4.1
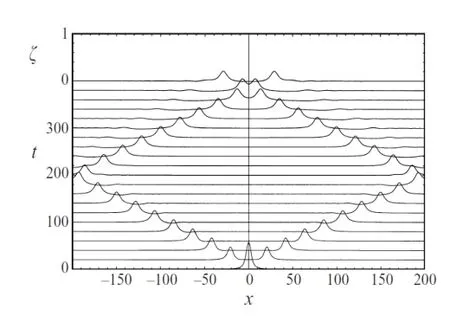
Figure 4.2
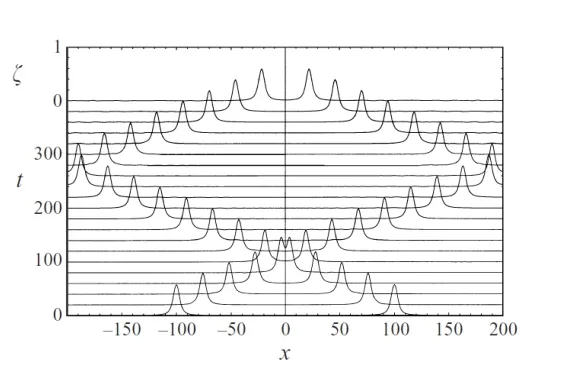
Figure 4.3
5 Other Mathematical Models of Long Nonlinear Internal Waves
5.1 Higher order KdV equation of internal solitary wave with free surface stratified shear flow
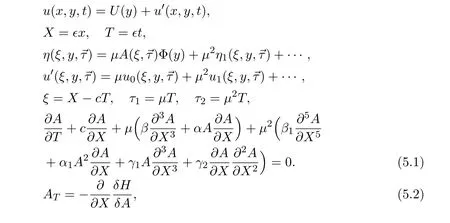
whereHhas the density
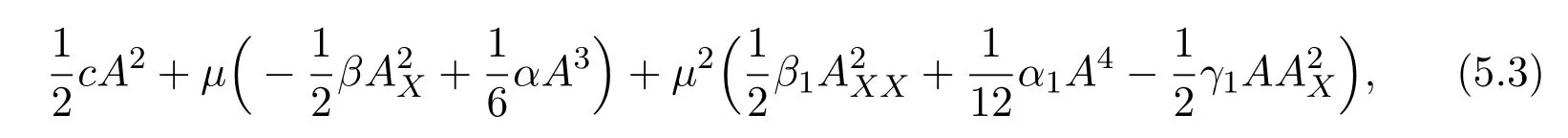
and generally
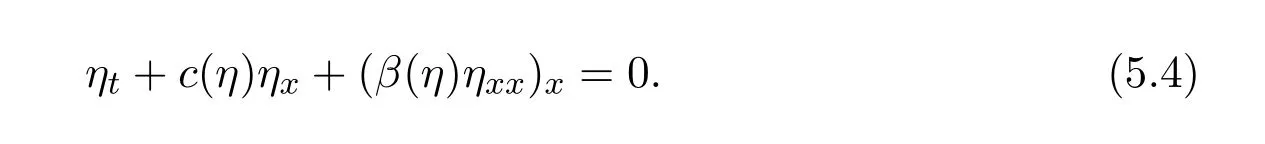
5.2 KP equation
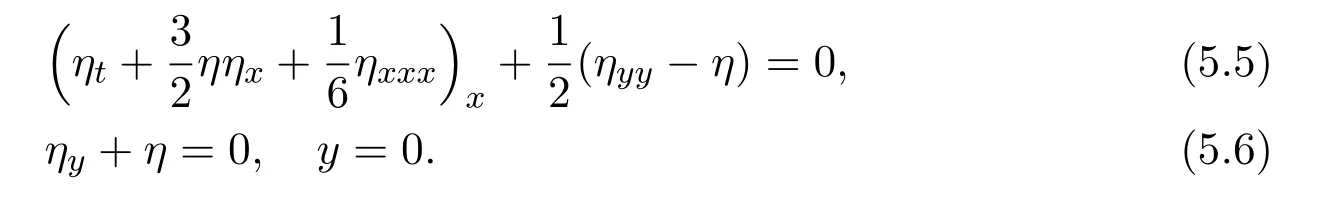
5.3 Rotation KP equation
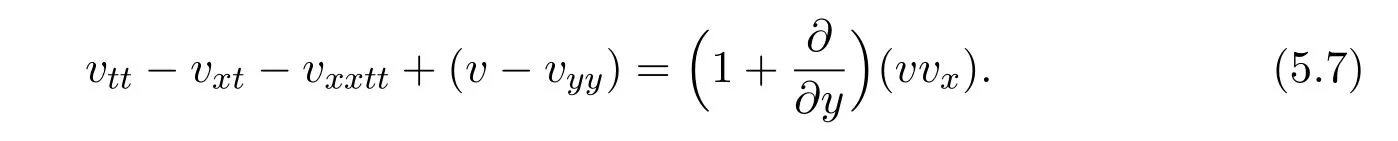
5.4 Another kind of shallow water wave equation
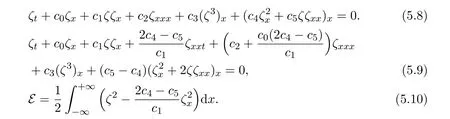
[1]V.Vlasenko,K.Hutter,Numerical experiments on the breaking of solitary internal waves over a Slope-Shelf topography,Journal of Physical Oceanography,32:6(2002),1779-1793.
[2]K.R.Helfrich,W.K.Melville,Long nonlinear internal waves,Annu.Rev.Fluid Mech.,38(2006),395-425.
[3]R.Grimshaw,E.Pelinovsky,O.Poloukhina,Higher-order Korteweg-de Vries models for internal solitary waves in a stratified shear flow with a free surface,Nonlinear Proc.Geopbys.,9(2002),221-235.
[4]K.G.Lamb,On boundary-layer separation and internal wave generation at the Knight Inlet sill,Proceedings Mathematical Physical&Engineering Sciences,460(2004),2305-2337.
[5]K.G.Lamb,K.P.Wilkie,Conjugate flows for waves with trapped cores,Pbys.Fluids.,16(2004),4685-4695.
杂志排行
Annals of Applied Mathematics的其它文章
- ESTIMATION OF PARAMETERS IN A CLOSED PYGMY POPULATION IN CAMEROON∗†
- A BLOCK-COORDINATE DESCENT METHOD FOR LINEARLY CONSTRAINED MINIMIZATION PROBLEM∗†
- A COMMENSAL SYMBIOSIS MODEL WITH HOLLING TYPE FUNCTIONAL RESPONSE AND NON-SELECTIVE HARVESTING IN A PARTIAL CLOSURE∗†
- NEWDYNAMICINEQUALITIES FORDECREASING FUNCTIONS AND THEOREMS OF HIGHER INTEGRABILITY∗
- THE BOUNDS ABOUT THE WHEEL-WHEEL RAMSEY NUMBERS∗
- DYNAMICAL ANALYSIS OF A SINGLE-SPECIES POPULATION MODEL WITH MIGRATIONS AND HARVEST BETWEEN PATCHES∗†
