返回舱着水冲击过载近似模型建模与分析

房红军 杨雷

(1 航天东方红卫星有限公司，北京 100094) (2 中国空间技术研究院载人航天总体部，北京 100094)

载人飞船返回舱可以采取海上回收方式回收，返回舱着水时，舱体及乘员将承受冲击过载[1]。实践和分析表明，返回舱着水过程出现的冲击过载可能对乘员造成伤害[2]。阿波罗12号在与水面碰撞时姿态偏离5.5°～7.5°，导致15倍重力加速度(15gn)的着水冲击过载(“阿波罗”所有飞行任务中最严重的)，舱壁上的一台摄像机脱落，将一名航天员头部砸伤[3-4]。高出允许范围的冲击载荷会威胁到航天员的安全，关系到任务的成败，因此在飞船设计阶段需要对该过程的特性有足够的了解。

国内外对返回舱着水冲击问题进行了大量理论和试验研究。在分析返回舱着水冲击过载的统计特性、恶劣着水工况及设计安全着水初始条件的过程中，往往需要获取大量不同工况条件下的着水冲击过载。其主要方法有理论公式、物理试验和数值计算[5]。目前，解析形式的理论公式难以求解返回舱这种以复杂外形和姿态入水的问题；而面对数千次以上的工况量，也难以通过物理试验完成。较为常用的手段是采用有限元等数值计算方法，基于通用瞬态动力学分析软件，求解返回舱着水冲击这一固、液、气耦合问题[5]。例如，NASA的星座计划中，使用LS-DYNA瞬态动力学分析程序计算猎户座(Orion)飞船乘员舱的着水冲击过载，进而结合蒙特卡罗仿真分析得到“统计上可行”的着水条件，用于飞行任务设计[6]。然而，基于有限元等数值计算方法求解返回舱着水问题，对计算资源的要求非常高。此外，随着舱体模型复杂程度的增加，所需计算时间会成倍增长，这极大限制了可分析的工况量。

本文采用克里金(Kriging)方法建立返回舱着水冲击过载的近似模型，建模过程所需的样本工况通过拉丁超立方抽样(LHS)方法获取，样本工况下的冲击过载通过有限元模型计算。该近似模型能够快速、准确地计算返回舱着水冲击过载，可有效提高返回舱着水条件设计及着水安全性分析的效率。

1 近似模型建模

近似模型(Metamodel)是根据原问题若干采样点拟合出来的，是反映原问题的输入与输出之间关系的近似数学模型，在某些领域也称为代理模型(Surrogate Model)或响应曲面模型，是一种数据拟合(插值或逼近)[7-9]。常用的近似模型有响应曲面模型、径向基函数模型和Kriging模型。

返回舱着水冲击过载问题如图1所示，返回舱以某一速度、姿态着陆在某一状态的海浪上，产生一定的冲击过载。考虑到返回舱及海浪真实运动过程的复杂性，以及着水时间短暂，将问题进行一定的简化：仅考虑返回舱的平动速度，忽略转动速度；海浪采用简化模型描述。

返回舱着水冲击过载近似模型建模的任务是建立返回舱着水状态与着水冲击过载之间的近似关系，建模流程如图2所示。近似模型建模的依据是若干样本工况以及样本工况下返回舱的着水冲击过载，其中，样本工况是经过挑选的若干返回舱着水状态(即着水工况)，为提高建模效率，同时保证准确度，本文通过试验设计方法中的LHS方法选择样本工况。综合考虑实现难度、结果准确度等因素，采用有限元模型计算出样本工况下返回舱的着水冲击过载。根据样本工况以及对应的冲击过载，采用Kriging方法即可建立着水冲击过载的近似模型。

图1 返回舱着水问题示意Fig.1 Capsule water landing scenario

图2 返回舱着水冲击过载近似模型建模过程

1.1 近似模型输入输出分析

首先，需要确定近似模型的输入参数及这些参数的范围。对于图1所示的返回舱着水问题，可通过返回舱的6个绝对运动参数(3个平动速度和3个姿态角)和海浪的6个运动参数描述，即工况条件。但是，设计变量越多，近似模型的维度就越高，需要的样本工况数量会急剧增加。进行进一步的简化[10]，将海浪等效为接触点处的无限大平面，并忽略海浪的水平速度，选择返回舱相对海浪的5个运动参数作为近似模型的输入，即法向速度、切向速度、俯仰角、偏航角和滚动角。5个相对运动参数的具体值可以根据运动学关系由舱体和海浪的绝对运动参数转换得到[10]，分析工程中返回舱实际的着水需求和特性，设计各参数的范围(即近似模型的适用范围)如表1所示。

表1 近似模型输入参数

工程中关注的返回舱着水冲击过载，包括乘员、结构、仪器设备等位置的数据，考虑到本文采用刚性体有限元模型计算样本工况下返回舱的着水冲击过载，因此只选取质心处加速度的峰值作为近似模型的输出，其他位置的过载数据可根据运动学关系换算得到。冲击过载的另一个重要特性是增长率，本文也选取质心处过载到达峰值的时间作为近似模型输出，以反映过载到达峰值的速度。

1.2 样本工况抽样

在确定了近似模型的输入参数及范围后，需要通过抽样方法得到具体的样本工况，进而通过有限元方法计算响应输出。近似模型是根据样本点数据对原问题其他位置的数据进行拟合得到的，因此，样本工况的选择对近似模型的准确程度至关重要，本文采用LHS方法。LHS方法属于充满空间的设计方法，设计点具有随机性，适用于基于计算机仿真试验的近似模型构造[11]。为获取更加优良的样本工况，本文采用最大最小距离准则[12]下的对称LHS设计方法，在表1的范围内，抽取300个样本工况。

1.3 近似模型

F(x)=M(x)+Z(x)=∑Pφ(x)+Z(x)

(1)

式中：M(x)为趋势项；Z(x)为均值为零的平稳随机函数，且该随机函数的协方差E [Z(w)Z(x)]满足式(2),只与点的距离有关，各向同性；P为随机变量；φ(x)为一普通基底函数。

E [Z(w)Z(x)]=σ2R(θ,‖w-x‖)

(2)

式中：w为变量；σ2为F(x)的方差；R(θ,‖w-x‖)为待定的基底函数，其中，θ为该基底函数的待定参数。

Kriging方法就是在随机函数F(x)的线性模型中求解其最小方差线性无偏估计。本文选择M(x)为随机多项式，根据最小方差要求和无偏要求，采用Lagrange乘子法，可得

f*(x)=m(x)+rTR-1(Y-m)

(3)

式中：未知点x与样本工况点{si}之间的相关列阵r=(R(θ,x,si))N×1，N为样本工况点总数，i为样本工况点序号；样本工况点{si}的协方差矩阵R=(R(θ,sj,sk))N×N，j，k为样本工况点序号；样本工况点{si}的响应值Y=(f(si))N×1；m(x)为随机过程F(x)的期望函数，一般未知，见式(4)；样本工况点{si}上m(x)的函数值列阵m=(m(si))N×1。

m(x)=E (F(x))=E (∑Pφ(x))=φTβ

(4)

式中：本文选择的基底函数列阵φ=(φ(x))B×1=(xξ)B×1，ξ为多项式阶数，B为基底函数列阵维数；β为随机向量(P)B×1的期望。

同样，可根据最小方差及无偏的要求，估计为

β*=(ΦTR-1Φ)-1ΦTR-1Y

(5)

式中：样本工况点的基底函数值矩阵Φ=(φ(si))N×B。

结合式(4)和式(5)，可得到m(x)的估计m*(x)，以及m*=(m*(si))N×1。

根据式(4)和式(5)，估计随机过程的方差为

(6)

本文取随机过程F(x)的自相关函数为Gauss型，即

(7)

式中：q为变量元素序号。

对于式(7)中的未知参数θ，采用极大似然估计的方法，引入似然函数，结合最优化方法求解。本文结合Kriging建模工具箱DACE[15]进行建模，该工具箱使用模式搜索法确定最优θ，则最终给出原响应函数的Kriging近似模型为

(8)

2 近似模型误差与效率分析

作为算例，本文采用Matlab工具箱Model-Based Calibration进行LHS，抽取返回舱着水的300个样本工况和20个检验工况；采用LS-DYNA软件建立返回舱着水有限元模型，计算300个样本工况下返回舱的着水冲击过载，对计算结果进行截断及滤波处理后，采用Matlab工具箱DACE(Kriging近似模型建模工具箱)建立着水冲击过载峰值及峰值时间的Kriging近似模型。

2.1 近似模型误差分析

本文采用独立的检验点检验近似模型的误差，以返回舱质心处纵向(X轴)过载为例，图3和图4分别给出了20个检验点处近似模型的预测结果与有限元模型计算结果的对比。可见，在各种工况下，近似模型对舱体过载峰值以及到达过载峰值的时间的拟合程度均较高。

(9)

(10)

(11)

式中：Nc为检验点的数量；t=1，2，…，Nc。

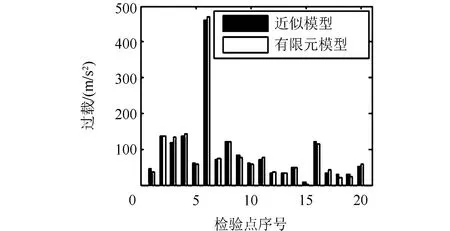
图3 返回舱质心X轴向过载峰值Fig.3 Centroid peak loads along X axis of capsule

图4 返回舱质心X轴过载到达峰值时间Fig.4 Time of centroid peak loads along X axis of capsule

在20个检验工况上，近似模型对过载峰值预测的偏差统计如表2所示。可见，返回舱质心过载响应近似模型的最大偏差在15 m/s2以下，均方根偏差与平均偏差普遍在7 m/s2以下，而对返回舱安全构成威胁的冲击过载峰值一般在100 m/s2以上[16]，这样的偏差是在工程可接受的范围内。结合图3可判断，本文建立的返回舱质心处着水冲击过载的近似模型，在全局和局部的准确程度均比较高。

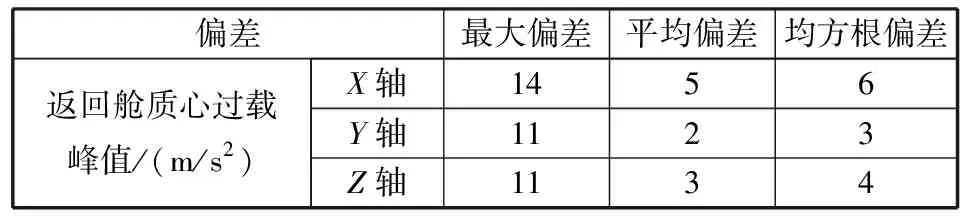
表2 近似模型的偏差

2.2 近似模型计算效率分析

完成近似建模后，可对冲击过载进行快速预测。以返回舱着水冲击问题的蒙特卡罗仿真分析为例，随机抽样5000个工况，分别使用有限元模型和近似模型进行计算。表3给出了2种模型计算耗时的对比，其中近似模型的计算耗时考虑了样本工况和检验工况的计算过程耗时。本文采用高性能计算系统进行有限元模型计算，单次计算耗时30 min；采用普通计算机(2.93 GHz处理器×2)进行近似模型的计算。

由表3可见，在抽样量为5000时，结合少量的有限元计算结果建立近似模型后进行蒙特卡罗仿真，所需计算时间仅是完全采用有限元模型的6.4%，效率提高约16倍；并且，当抽样量增加时，有限元模型的蒙特卡罗仿真计算耗时的增长是线性的，而近似模型的仿真耗时基本不会增长。

3 结论

本文利用LHS方法抽取了返回舱着水样本工况，采用有限元模型计算了样本工况下着水冲击过载结果，以样本工况和工况结果为输入，选用Kriging方法建立返回舱着水冲击过载的近似模型。经过与有限元模型进行准确度和计算效率对比，表明这种近似模型可以较为高效、准确地完成返回舱着水冲击过载计算。

(1)通过合理地选择样本工况，利用少量的有限元计算，采用Kriging方法，能够建立返回舱着水冲击过载(峰值与峰值时间)的近似模型，并较为准确地对返回舱着水冲击过载峰值进行预测。在本文抽取的20个检验工况上，峰值过载的最大偏差不超过15 m/s2，平均偏差不超过7 m/s2。

(2)近似模型能够对返回舱的着水冲击过载进行高效计算，对于抽样量为5000的蒙特卡罗仿真，采用近似模型与有限元模型相比，效率提高约16倍。

(3)近似模型能够对返回舱的着水冲击过载进行准确高效的预测，为恶劣工况判断、安全着水初始条件设计及着水过程的蒙特卡罗仿真提供了一种有效的解决途径。

参考文献(References)

[1] 戚发轫，朱仁璋，李颐黎.载人航天器技术[M].2版.北京：国防工业出版社，2003：17-18

Qi Faren, Zhu Renzhang, Li Yili.Manned spacecraft technology [M]. 2nd ed. Beijing: National Defense Industry Press, 2003: 17-18 (in Chinese)

[2] Lawrence Charles, Littell Justin D, Fasanella Edwin L. Orion crew member injury predictions during land and water landings, NASA/TM-2008-215171 [R]. Washington D.C.： NASA, 2007

[3] Johnston R S, Dietlein L F， Berry C A. Biomedical results of Apollo， NASA-SP-368 [R]. Washington D.C.： NASA, 1975

[4] Woods W D. How Apollo flew to the moon [M]. Berlin： Springer, 2007

[5] 房红军,杨雷.载人飞船返回舱着水冲击问题研究进展[J].载人航天,2013,19(6):76-83

Fang Hongjun, Yang Lei. Review on water landing impact problems of manned reentry capsules [J]. Manned Spaceflight, 2013, 19(6): 76-83 (in Chinese)

[6] Bryan K Smith, Richard Bouchard, Chung-Chu Teng, et al. Assessment of ocean wave model used to analyze the Constellation Program (CxP) Orion project crew module water landing conditions， NASA/TM-2009-215752 [R]. Washington D.C.： NASA, 2009

[7] 陈余军,周志成,曲广吉.多学科设计优化技术在卫星设计中的应用[J].航天器工程,2013,22(3):16-24

Chen Yujun, Zhou Zhicheng, Qu Guangji. Application of multidisciplinary design optimization in satellite design [J]. Spacecraft Engineering, 2013, 22(3): 16-24 (in Chinese)

[8] 李恩颖.近似模型优化体系关键技术研究及应用[D].长沙：湖南大学,2009

Li Enying. The key of research and application of metamodel-based optimization [D]. Changsha: Hunan University, 2009 (in Chinese)

[9] 穆雪峰,姚卫星,余雄庆，等.多学科设计优化中常用代理模型的研究[J].计算力学学报,2005,22(5):608-612

Mu Xuefeng, Yao Weixing, Yu Xiongqing, et al. A survey of surrogate models used in MDO [J]. Chinese Journal of Computational Mechanics, 2005, 22(5)： 608-612 (in Chinese)

[10] Arthur M Whitnah, D B Howes. Statistics concerning the Apollo command module water landing, including the probability of occurrence of various impact conditions, successful impact, and body X-axis loads， NASA-TM-X-2430 [R]. Washington D.C.： NASA, 1971

[11] 游海龙,贾新章,张小波，等.试验设计与仿真相结合构造集成电路元模型的方法研究[J].电子学报,2006,36(6):1159-1162

You Hailong, Jia Xinzhang, Zhang Xiaobo, et al. Study on the method of the design of experiment integrated with simulation for constructing the integrated circuit metamodel [J]. Acta Electronica Sinica, 2006, 36(6): 1159-1162 (in Chinese)

[12] Jared L Deutsch, Clayton V Deutsch. Latin hypercube sampling with multi-dimensional uniformity [J]. Journal of Statistical Planning and Inference, 2012, 142: 763-772

[13] Anoop A Mullur, Achille Messac. Metamodeling using extended radial basis functions: a comparative approach [J]. Engineering with Computers, 2006, 21: 203-217

[14] 吴宗敏.散乱数据拟合的模型、方法和理论[M].北京：科学出版社，2007

Wu Zongmin. Model, method and theory of fitting disheveled data [M]. Beijing: Science Press, 2007 (in Chinese)

[15] Søren N Lophaven, Hans Bruun Nielsen, Jacob Søn￣der￣gaard. DACE-a Matlab Kriging toolbox， Technical Report IMM-TR-2002-12 [R]. Kongens Lyngby： Technical University of Denmark, 2002

[16] NASA. Human integration design handbook (HIDH)， NASA/SP-2010-3407 [S]. Washington D.C.：NASA, 2010