变速器传动轴变形对齿轮传递误差的影响分析

2018-07-05郑光泽陈雪松田联明黄修鹏

重庆理工大学学报(自然科学) 2018年6期

郑光泽,陈雪松,田联明,黄修鹏

(1.重庆理工大学车辆工程学院，重庆 400054； 2.株洲欧格瑞传动股份有限公司，湖南株洲 412000; 3.重庆清研理工汽车检测服务有限公司，重庆 401329)

齿轮传递误差(TE)即齿轮理论啮合点与实际啮合点在啮合线上的位移差，是齿轮产生啸叫的激励源[1]。变速器系统(传动轴、轴承、壳体)变形会对齿轮传递误差产生影响，传动轴、轴承、壳体变形均会叠加到齿轮与传动轴关联点。因此，研究齿轮与传动轴关联点的各自由度变形对齿轮传递误差的影响具有重要意义。

纵观国内外学者对齿轮传递误差问题的研究，减小齿轮传递误差的基本方向主要集中在齿轮微观修形或提高齿轮精度[2-4]上。但是，随着研究逐渐深入，越来越多的学者开始从系统的角度去研究减小齿轮传递误差的方法。李杰等[5]通过建立变速器齿轴系统分析模型，分析了传动轴变形对齿面接触区域的载荷分布以及齿轮啮合最大接触应力的影响。白恩军等[6]通过有限差分法计算了传动轴的变形量，对比分析了传动轴为刚性和柔性2种情况下齿轮啮合情况的变化，结果表明：传动轴弯曲变形与扭转变形的耦合会影响齿轮的啮合特性。张靖等[7]结合试验与仿真，分析了轴承刚度对齿轮啮合情况的影响，结果表明：适当增大轴承刚度有助于改善齿轮啮合特性。何畅然等[8]在考虑变速器壳体为柔性体前提下，对齿轮重合度、传递误差、齿面接触应力以及变速器振动响应等相关参数进行了数值计算，通过对齿轮宏观参数及微观参数进行优化减小了齿轮传递误差。

上述研究虽考虑了传动轴、轴承、壳体对齿轮传递误差的影响，但在将各部件的变形叠加到齿轮与传动轴关联点以及齿轮与传动轴关联点的各自由度的变形对齿轮传递误差的影响研究方面还存在一定的不足。

本文以某单对齿变速器为研究对象，建立了只考虑传动轴变形的齿轴系统仿真分析模型，研究了传动轴刚度对齿轮传递误差的影响以及传递误差对传动轴各自由度变形的敏感度。本文中定义齿轮与传动轴关联点为齿轮沿齿宽方向的中间截面所对应的传动轴中心点。

1 齿轴仿真分析模型建立

本文研究对象为一单对齿变速器。其中输入齿轮为轴齿、输出齿轮与输出轴固连在一起。为避免壳体和轴承变形对齿轮啮合产生影响，模型建立过程中不加入壳体有限元模型，同时将轴承设置成概念轴承，并将轴承各自由度刚度值设置成较大值(近似为刚性)。建立的齿轴系统的结构简图如图1所示。

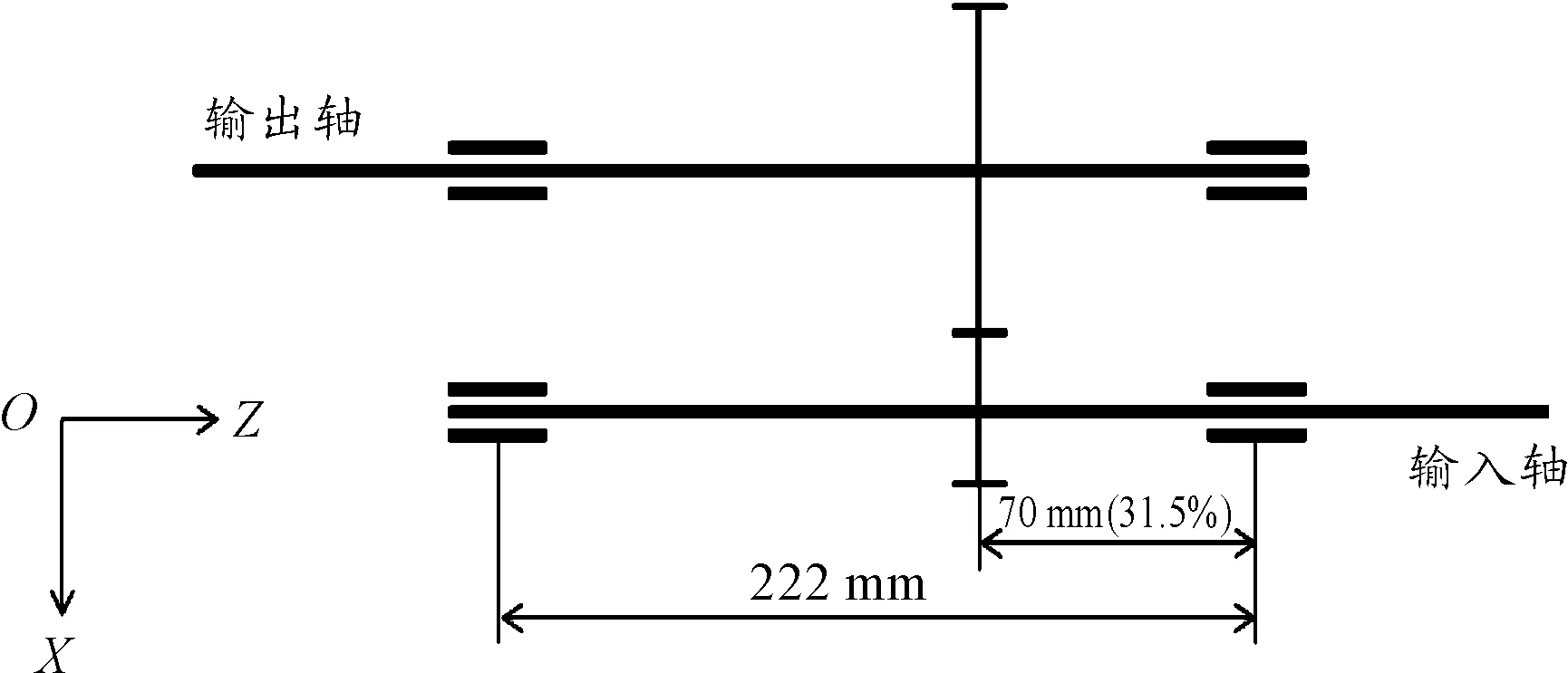
图1 齿轴系统结构简图

齿轮材料为20CrMnTiH、传动轴材料为20CrMnTi。材料参数如表1所示，齿轮主要参数如表2所示。

表1 材料参数

表2 齿轮副基本参数

2 传动轴变形对齿轮传递误差的影响

在由齿轮传递误差所引起的变速器壳体振动与辐射噪声中，包含了各阶对应齿轮啮合阶次的成分分量。一般情况下，第1阶所占比例较大，因此本文以齿轮的1阶传递误差作为关注点，研究传动轴变形对齿轮1阶传递误差的影响。

2.1 不同扭矩下传动轴变形对齿轮传递误差的影响

在单独考虑传动轴变形情况下，齿轮传递误差同时受到传动轴变形和齿轮自身变形的影响。不同扭矩下，轮齿和传动轴会产生不同程度的变形，因此在不同扭矩下传动轴的变形对齿轮传递误差的影响程度也会发生变化。

输入输出轴的变形关注点为齿宽中间位置对应点，如图2所示，其中：输入轴为O1点；输出轴为O2点。

图2 输入输出轴变形位置

分析时，首先分别计算10%Nmax、20%Nmax、40%Nmax、60%Nmax、80%Nmax、100%Nmax(Nmax为230 N·m)不同扭矩下齿轮传递误差的变化；然后在相同扭矩下，在O1、O2点施加5个自由度(除绕Z轴扭转自由度)的静态载荷，从而平衡原有载荷在O1、O2点处引起的变形(绕Z轴的扭转变形除外)，使O1、O2点在X、Y、Z、RX、RY自由度的变形量为0。理论上讲，传动轴绕Z轴的扭转变形，只会引起整个齿面的一致转动，对齿轮的实际啮合情况，其主要是延迟或提前一对齿轮副的啮合时间，并不会引起齿轮副实际啮合点产生变化，因此传动轴变形对齿轮传递误差的影响未考虑O1、O2点绕Z轴的转动变形量。分析结果如图3所示。

图3 不同扭矩下传动轴变形对齿轮传递误差的影响

由图3可知：

1) 在不考虑传动轴变形情况下，传递误差的变化完全由齿轮变形所引起，随着扭矩的不断增大，传递误差呈现出先增大后减小再增大的变化趋势；扭矩从较低值开始增加，传递误差增大主要是由于齿轮变形的增加所引起；随着扭矩逐渐增大，传递误差却逐渐减小，主要是由于扭矩的增大会引起齿轮弹性变形增大，参与啮合的齿面面积增多，实际啮合线长度也会增长，从而使齿轮啮合刚度增大，减小了齿轮啮合过程中啮合线上的变形波动[9]。随着扭矩的进一步增大，传递误差呈逐渐增大的趋势，主要是由于随着扭矩不断增大，当齿轮的弹性变形在增大一定程度时，参与啮合的齿面面积已增大到最大值，但齿轮啮入啮出时的变形却依然逐渐增大，从而增大了齿轮啮合过程中啮合线上的变形波动。

2) 在考虑传动轴变形情况下，传递误差与不考虑传动轴变形时的变化趋势保持一致，中低扭矩下(10%Nmax～60%Nmax)，2条曲线基本贴合，说明在中低扭矩下传动轴的变形并未对齿轮产生明显影响；从60%Nmax开始，大概到85%Nmax范围，随着扭矩的不断增加，2条曲线之间的差值越来越大，说明传动轴变形对齿轮传递误差的影响越来越大，这主要是由于传动轴的变形逐渐增大，与此同时齿轮的自身弹性变形对传递误差的影响在逐渐减小；当扭矩超过85%Nmax时，2条曲线的差值又呈现减小趋势，主要是由于在此扭矩范围内，齿轮自身的弹性变形再次加剧了齿轮差递误差的增大，对传递误差的变化起主导作用。

2.2 齿轮传递误差对传动轴变形的灵敏度分析

在中高扭矩下，传动轴变形会对齿轮传递误差产生影响，但传动轴的变形是由6个自由度(3个转动、3个平动)的变形组合而成，具体哪一个自由度的变形对齿轮传递误差的影响起到决定性因素，以及齿轮传递误差对传动轴6自由度的变形的敏感度还需进一步分析。

采用同样的方法，通过在O1、O2点施加静态载荷来控制传动轴在O1、O2点的变形。由于输入输出轴在O1、O2点的变形对齿轮传递误差的影响具有同等的意义，因此以输入轴O1点的变形作为关注点，分析时通过施加静态载荷使O2点的变形在X、Y、Z、RX、RY自由度的变形始终保持为0，然后依次改变输入轴O1点的静态载荷，使O1点在X、Y、Z、RX、RY自由度的变形量分别为0、±5、±10 μm/mrad。单独分析1个自由度的变形量对齿轮传递误差的影响时，其余自由度的变形量始终保持为0(绕Z转动变形除外)。之前已分析，在大扭矩下，传动轴变形将会对齿轮传递误差产生较为明显的影响，故分析时输入扭矩设置为80%Nmax。最终分析结果如图4所示。

图4 各自由度变形对传递误差的影响

由图4可知：

1) 同等变化量情况下，传动轴绕X轴转动变形对齿轮传递误差的影响最大，绕Y轴的转动变形造成的影响次之，X、Y、Z三方向的平移几乎对齿轮传递误差没有影响。

2) 相同转动弧度情况下，由于转动方向的不同，齿轮传递误差的变化量也会不同，传动轴在绕X、Y轴负方向的转动将会引起更大的齿轮传递误差的变化。

3) 之所以在同一自由度不同方向的转动变形会引起不同齿轮传递误差的变化，主要原因为：齿轮在受载情况下会产生一定的变形，一定程度上齿轮的变形可分解到6个自由度上，所以齿轮的变形也存在方向性。当传动轴变形方向与齿轮变形方向一致时，将会加剧齿轮传递误差的变化；当传动轴变形方向与轮齿变形方向相反时，传动轴的变形量中有一部分会用来抵消轮齿的变形，齿轮传递误差在这种情况下可能会先减小再增大。

绕X、Y轴的转动变形会引起更大的齿轮传递误差的变化，其原因主要是传动轴绕X、Y轴的转动变形最终体现到齿轮上的相对位移差，将会引起齿轮在沿齿宽方向上的前后差异。同时传动轴绕X、Y轴的转动变形也可转换为传动轴轴线平行度的变化。如图5所示，f∑δ代表轴线平面上的偏差，f∑β代表垂直平面上的偏差，因此本文中传动轴绕X轴的转动变形可体现为传动轴在垂直平面的偏差，传动轴绕Y轴的转动变形可体现为传动轴在轴线平面的偏差。X方向的平移可视作中心距的变化。

图5 轴线平行度示意图

有研究学者得出结论：相比之下，中心距偏差对齿轮传递误差的影响较小，轴线平行度偏差对齿轮传递误差的影响较大；轴线平面内的轴线偏差将影响齿轮螺旋线啮合偏差。它的影响是工作压力角的正弦函数，而垂直平面上的轴线偏差则是影响工作压力角的余弦函数，垂直平面上的偏差所导致的啮合偏差将比同样大小的轴线平面内偏差导致的啮合偏差大2～3倍[10]。本文研究得出的结论与以上学者得出的结论基本吻合。

综上所述，齿轮传递误差对传动轴绕X轴(中心距方向)转动变形的敏感度最高，对绕Y轴(齿轮圆周力方向)转动变形的敏感度次之。

2.3 传动轴弹性模量对齿轮传递误差的影响分析

通过本文的分析可知：齿轮传递误差对传动轴绕X、Y轴的转动变形是最敏感的。传动轴的材料特性(弹性模量)、轴径大小和齿轮安装位置等因素均会对传动轴变形产生影响。因此，通过改变传动轴的弹性模量可以对齿轮传递误差进行优化。

在本文2.1节分析模型基础上，分析工况设置为2 100 r/min、80%Nmax。通过控制变量法，依次改变输入、输出轴的弹性模量，如表3所示。分析输入、输出轴在X、Y、Z方向的位移和绕X、Y轴转动弧度的变化，同时分析齿轮传递误差的变化情况。分析结果如图6、7所示。

表3 输入输出轴弹性模量变化情况

在情形1、情形2下，分别控制输出轴、输入轴的弹性模量不变，从而可以分析出单独1根传动轴弹性模量变化时对齿轮传递误差的影响。但是由于在改变输入输出轴弹性模量时对应的另1根轴并非为刚性，也存在变形，因此在分析结果中给出了两根轴的相对变形，如图8～11所示。

图6 输入轴弹性模量变化对齿轮传递误差的影响

图7 输出轴弹性模量变化对齿轮传递误差的影响

图8 Case1输入轴相对输出轴X、Y、Z方向位移的变化

图9 Case1输入轴相对输出轴绕X、Y轴转动的变化

图10 Case2输入轴相对输出轴X、Y、Z方向位移的变化

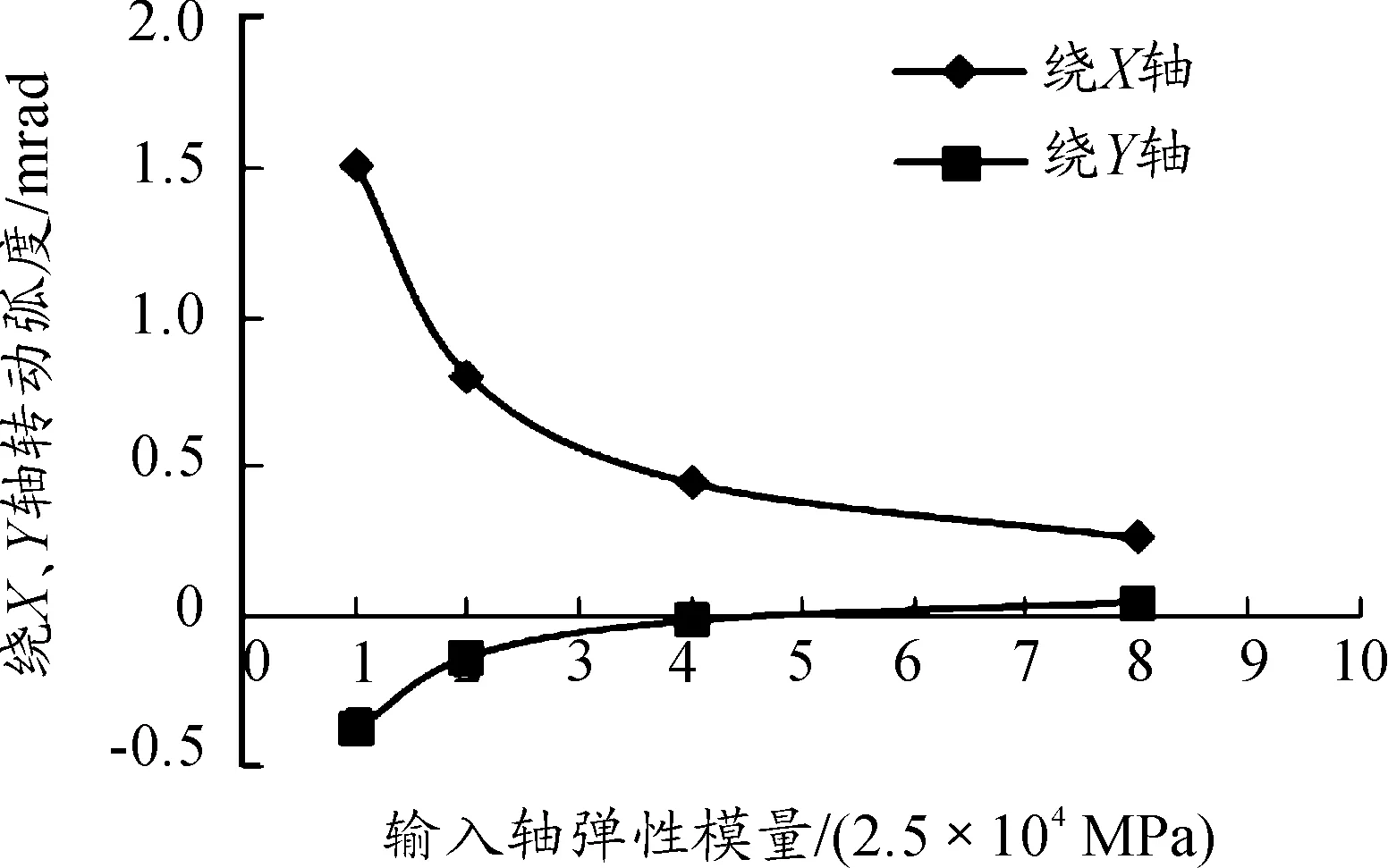
图11 Case2输入轴相对输出轴绕X、Y轴转动的变化

通过分析得出：

1) 情形1：随着输入轴弹性模量的增大，1阶传递误差幅值从0.288 3 μm减小到 0.287 0 μm，减小量非常微小，几乎没有减小；

2) 情形2：随着输出轴弹性模量的增大，1阶传递误差幅值逐渐减小；幅值从 0.376 1 μm减小到0.157 0 μm，减小比例为58.2%。

3) 之所以改变输出轴的弹性模量，使1阶传递误差减小的比例更高，是因为在情形2中，传动轴绕X轴转动变形减小的幅值更大，从1.51 mrad减小到0.26 mrad，减小了1.25 mrad；而在情形1中，只是从-0.409 4 mrad变化到-0.263 9 mrad，变化量为0.145 5 mrad；

4) 2种情形下绕X轴转动变形量变化的幅度不同，主要是由于2根轴所受载荷不同引起：齿轮副存在传动比，该对齿轮的传动比为2.04，在同一输入扭矩下，输出轴会承受更大的载荷，从而引起更大的传动轴变形，因此在实际分析过程中，更应关注输出轴的变形。

2.4 齿轮安装位置对齿轮传递误差的影响分析

通过理论分析可知：齿轮安装点据后轴承的距离占前后轴承距离的比例在0.788 6和0.211 3两点处时RX取得极大值。

在传动轴上选取5个齿轮安装位置，计算出在工况2 100 r/min、80%Nmax情况下，不同位置处的齿轮传递误差。输入轴上5个齿轮安装位置如图12所示:s1为第1个齿轮安装位置，从左至右位置后依次递增，最右侧s5为第5个齿轮安装位置，5个齿轮安装点距后轴承的距离与前后轴承的距离比值分别为10%、30%、50%、67%、82%，输出轴上齿轮的安装位置与输入轴上的位置相对应。分析结果如图13所示。