浅议小学生思维素质的培养
2018-07-05谢良平
谢良平
(福建省三明市建宁县溪源中心小学,福建 三明)
素质的培养,是现代教育对我们教育工作者提出的一个基本要求。小学生各方面的素质正处于一个飞速发展的时期,学校素质教育工作开展得如何,对学生今后的发展起着举足轻重的作用。作为学校教育的重要组成部分,小学数学课堂教学也应当遵循这一教育基本原则。人的素质培养应当是多方面的,本文就其中的一项重要任务——思维素质的培养,谈谈自己的一些浅见。
一、趣味导入,激发思维,培养思维的批判性
上课伊始,小学生们往往停留在课间活动的兴奋之中,难于迅速调整进入学习状态。良好的开端等于成功的一半。因此,在新课导入的方式选择上,教师应当认真斟酌。精彩的课堂导入,可以让学生迅速进入学习、思维状态,自然而然地进入学习新知的情境,激发学生的学习兴趣,从而有效提高课堂效率。我常用的新课导入方式有以下几种:操作式、诱新式、竞赛式、悬念式、讲故事、讨论……
例如,教学“圆柱体积的计算”这一课时,我利用“操作式”和“诱新式”相结合的新课导入方法:复习完长方体、正方体体积的计算公式后,我拿出一个平均分成若干份的圆柱体模型,向学生提问:“这是什么形状的物体?”“你会求它的表面积吗?”“怎么求?”从学生回答的语气中,我听出学生觉得这些问题太简单了。于是,我接着问:“你们能求它的体积吗?”见学生面有难色,于是,我提醒学生和我一起观察这个模型。很快,一位同学举起了他的小手,说:“老师,我能上台试试吗?”我同意了。他把这个模型拼成了一个近似的长方体后,说明“我们只要求出这个长方体的体积,就求出了圆柱体积”。沿着这一思路,我们顺理成章地推导出了圆柱体积的计算公式:V=sh。
按说,这节课的主要任务已经完成了:学生通过自己的操作探索,总结出了圆柱体积的计算公式。我正准备进入练习环节时,有一位平时爱动脑筋的同学大声说:“老师,我有不同的看法。”为了不打击他的积极性,我让他说出自己的见解——圆柱体积的计算公式还可以是底面周长的一半乘底面半径再乘高,即我愣了一下,立即明白了这个公式的由来。可我还是装糊涂,“这样可以吗?”我大声反问。这位同学脸涨得通红,急了,“这样可以,可以……”说话开始有些语无伦次,手中还拿起了他自己准备的圆柱体模型,其他同学表情一片愕然(不理解这样做的原因),于是,我让这位同学边演示拼摆过程,边解说——得到的这个近似的长方体的长a是圆柱体底面周长C的一半,宽b是圆柱体底面半径r,高h还是圆柱体的高h,长方体的体积计算公式是V=abh,所以圆柱体积的计算公式还可以是底面周长的一半乘底面半径再乘高,即。“哦……”,这位同学的话音刚落,同学们一片欢呼。这位同学精彩的解说不得不让人佩服。可见,新课导入方法的合理使用,有时能收到意想不到的结果。
二、培养初步概括能力,逐步地从具体形象到抽象思维过渡
在教学乘法交换律时,教师可引导学生观察算式12×10=120和10×12=120。因为这两个算式的结果相同,所以12×10=10×12。同样,23×21=21×23,还可以让学生自己举出类似的例子,如:457×32=32×457……从上述具体的例子中,引导学生从因数的位置与积的大小进行观察、比较,把硬性材料中具体的数逐步概括,引导学生用数学语言表达出乘法交换律。同样,乘法结合律、小数的意义、比例基本性质等数学知识,都是通过抽象与概括得出的,也可以用同样的方法进行教学。总之,数学中任一个数,任一个算式、公式、概念或规律,都是抽象概括而得出来的结果。
三、进行多角度的思维训练
教育现代化的核心是观念的现代化,尤其是教育价值的现代化,数学教学时,教师应该明确教学的目的不仅仅是掌握概念、规律、定理、公式等结论性知识,更重要的是要培养学生运用所学的知识和方法,解决简单的实际问题的能力,使学生能够触类旁通,活用知识。
我在教学“用比例知识解应用题”一课时,先出示例题:
“大齿轮与小齿轮的齿数比是4∶3。大齿轮有36个齿,小齿轮有多少个齿?”
教学时,我注意调动学生积极参与,引导学生根据不同的解题思路和数量关系,发挥学生在思维过程中的主动性和创造性,得出了多种不同的解题方法:
①解:设小齿轮有x个齿。

有的学生则想到:“小齿轮的齿数是大齿轮的出现更为简便的解法:
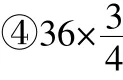
有的学生还采用其他的思维方法,从不同角度、运用不同解题方法来解答,拓展了思路,领略运用多种知识的乐趣,培养了自身的能力。
四、思维训练的同时,要考虑学生的情感因素
《义务教育数学课程标准》指出,对数学学习的评价要关注学生数学学习的水平,更要关注他们在数学活动中所表现出来的情感与态度。学生的认知过程总是伴随着情感,只有做到情理交融,互相促进,才能使学生各方面的素质和谐发展。所以,我们教育工作者在设计问题时,除了要考虑学生的认知水平,还要积极有效地创设问题情境,培养学生情趣,激发学生的学习动机。
例如,学了圆的面积计算之后,让同学们讨论:“一只小羊羔被一条4米长的绳子拴在大草坪中的一根木桩上,这只小羊羔能吃到草的范围有多大呢?”由于把圆的面积计算转化为一个富有故事情节的实际问题,很受学生欢迎。
当然,思维能力的培养不是一朝一夕就能完成的,这是一项复杂而艰巨的工程,这就要求我们教育工作者,特别是在教学第一线的教育者,不能单纯地“授人以鱼”,而应该“授之以渔”,持之以恒地加强学生思维能力的培养。
