PMO作用下连铸二冷区电磁场-流场-温度场的数值模拟

郝军利, 赵 静, 仲红刚,3, 徐智帅, 李仁兴, 翟启杰

(1.上海大学省部共建高品质特殊钢冶金与制备国家重点实验室,上海200072;2.上海大学上海市钢铁冶金新技术开发应用重点实验室,上海200072;3.上海大学上海材料基因组工程研究院,上海200072)

近年来,利用外加电磁场影响连铸的凝固过程一直受到国内外学者的关注,一些研究人员也提出了不同的电磁场凝固细晶技术,包括电磁搅拌技术[1-2]、电磁振荡技术[3]、脉冲磁场技术[4-5]以及脉冲磁致振荡技术[6-7]等.由于通过实验方法来进行高温熔体中的电磁场、流场及温度场分布的测定十分困难,因此为了进一步研究电磁场对金属凝固组织的影响规律,数值模拟逐步被接受,成为分析连铸过程的一种有效手段.黄军涛等[8]对方坯二冷区低频三相交流电产生的电磁搅拌进行数值模拟,得到了铸坯内部电磁场和流场分布特点.于海岐等[9]和陈伟等[10]利用不同方法进行了结晶器低频三相交流电产生的在电磁搅拌条件下的电磁场、流场等多场耦合分析.2007年,Gong等[6]、Liao等[7]和翟启杰等[11]提出了脉冲磁致振荡凝固细晶(pulse magneto oscillation,PMO)技术,通过将作用线圈作用于连铸机二冷区这一方式应用于连铸生产,在研究铸坯时发现脉冲磁致振荡技术可以细化凝固组织,减少中心疏松,提高等轴晶率,改善元素宏观偏析.为进一步探明PMO对连铸坯凝固过程的影响,本工作建立了在直径为178 mm圆坯二冷区脉冲磁致振荡条件下电磁场-流场-温度场耦合数学模型,采用ANSYS软件对电磁场、流场和温度场进行了数值模拟,模拟结果为现场工业试验优化设备参数提高了可靠的理论指导.

1 几何模型的建立

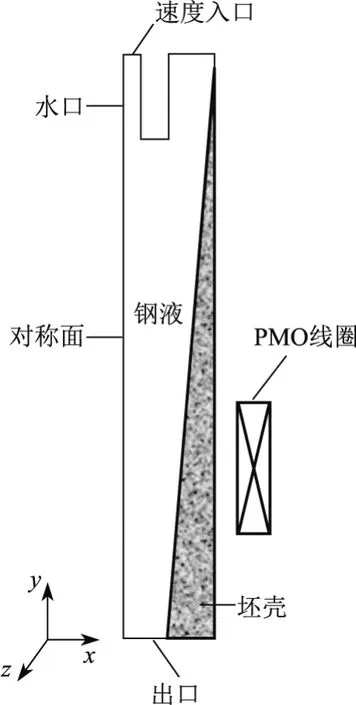
图1 本模型几何结构Fig.1 Geometry structure of this model

由于连铸圆坯和直水口具有轴对称性,故本工作在计算时应采用具有轴对称性的2维模型进行模拟计算,模拟空间内存在连铸熔体、连铸坯壳、线圈和空气层4个部分,由于线圈位于足辊段下面,故模拟还包括连铸结晶器、足辊段和部分二冷一段.模型的几何结构如图1所示,计算过程中所用到的参数由现场提供.圆坯的直径为178 mm,模型计算长度为2 000 mm.PMO装置位于足辊段下端(距弯月面1.2 m),拉速为1.8 m/min;水口为直通型,内径为30 mm,外径为90 mm,浸入深度为100 mm;钢液过热度为39°C,密度为7 100 kg/m3,粘度取值为0.006 2 kg/(m·s);比热容和热导系数随温度变化,钢液的电导率为7.14×105(Ω·m)−1,坯壳的电导率为1.0×105(Ω·m)−1,钢液和坯壳的相对磁导率均为1.0.

2 数学模型的建立

为了使计算模型能够得到求解,故做如下假设:

(1)线圈周围为开放性磁场,建立有限空间空气域,结合无限远边界条件来模拟无限大空间;

(2)钢液为不可压缩流体,电导率为各向同性;

(3)忽略钢液流动及温度变化对磁场的影响;

(4)忽略已凝固的坯壳对钢液流动的影响;

(5)模型具有较好的轴对称性,可简化为2维模型进行模拟.

2.1 电磁场控制方程

铸坯内部的电磁场分布规律符合Maxwell方程组:

式中,B为磁感应强度(T),E为电场强度(V/m),t为时间(s),H为磁场强度(A/m),J为感应电流密度(A/m2).

对于电磁场的计算,通过定义磁势A和标量电势φ,得到磁场偏微分方程和电场偏微分方程,进行求解得到

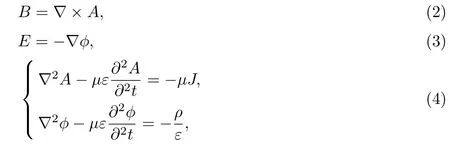
式中,µ为真空磁导率,ε为介电常数.

2.2 流场动量和能量控制方程

连续性方程:

动量方程:

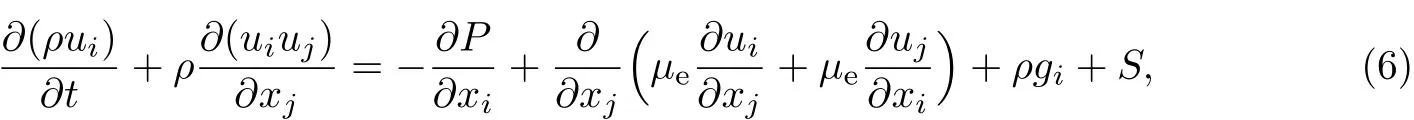
式中,ρ为钢液的密度(kg/m3),ui为沿坐标轴方向的速度矢量,P为作用在流体微元上的压力(N/m2),µe为有效粘度系数(m/s),S为动量源(N/m3),gi为第i个方向上的分量.

将式(7)中得到的电磁体积力以动量源的形式加载到动量方程中进行计算,电磁力F可表示为

能量方程:

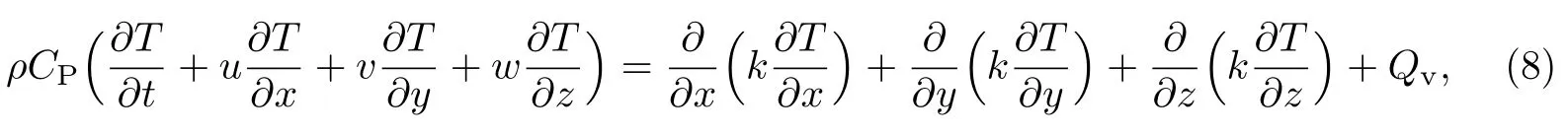
式中,CP为钢液比热容(J/(kg·m));T为热力学温度(K);k为热导率(W/(m·K));Qv为体积热源(W/m3);u,v,w为3个方向上的速度分量.

3 边界条件和求解方法

在计算电磁场时,空气域的外边界采用磁力线平行条件,线圈中载入脉冲电流.入口流速根据拉速由质量守恒定律计算得到,结晶器液面采用自由液面边界条件,结晶器壁面和二冷区壁面采用无滑移边界条件,对称面边界条件为对称轴上的法线分量为0,出口边界条件为出口处流动充分发展.水口入口温度为钢液浇注温度,自由液面为绝热边界条件,钢液壁面温度为钢液固相线温度.

计算过程分3步完成.首先,采用薄片移动法得到铸坯凝固厚度,假想在结晶器弯月面处形成一个薄片,此薄片根据拉速随铸坯而往下移动,在移动过程中薄片的凝固厚度和表面温度不断变化,以此得到铸坯凝固厚度;然后,将铸坯厚度加载到电磁场计算模型中,利用ANSYS模拟计算得到在脉冲磁致振荡条件下钢液内部电磁场分布;最后,计算并对比在有无脉冲磁致振荡作用时钢液内部流场和温度场的分布.

4 模拟结果与讨论

4.1 坯壳厚度的确定

由于圆坯具有对称性,故取圆坯断面作为研究对象,采用薄片移动法建立非稳态模型.传热过程是从弯月面开始,以圆坯实际拉速往下移动所经历的传热过程.

结晶器热流密度的计算公式为

式中,q为结晶器热流密度(W/m2);A,B为实验常数;t为时间(s).

二冷区传热系数与水流密度有关,由于实验条件不同,不同的研究人员所得的经验公式有所差异.本工作采用式(10)所示的计算公式[12]:

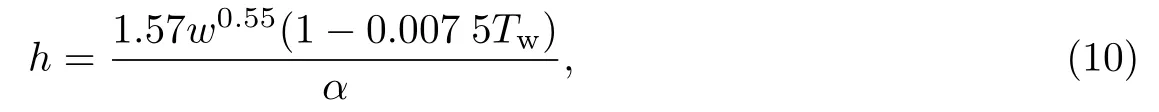
式中,h为传热系数(W/(m2·°C)),w为水流密度(L/(m2·s)),Tw为冷却水温度(°C),α为常数.

根据模型计算得到不同位置的坯壳厚度(见图2),其PMO施加位置的坯壳厚度为27 mm,工厂实测PMO施加位置的坯壳厚度为27.9 mm,误差率为3.22%,误差在条件允许范围之内.

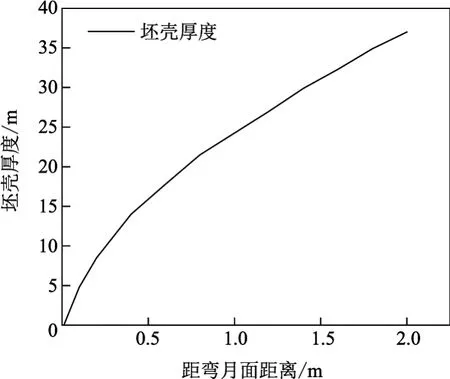
图2 不同位置的坯壳厚度分布Fig.2 Shell thickness distributions of diあerent locations

4.2 铸坯内部磁感应强度分布

由于脉冲电流具有周期性,铸坯内部的磁感应强度、电磁力等均随着脉冲电流周期性变化,因此在研究铸坯内部磁场问题时,只需要关注一个周期内电磁场变化情况即可.一个周期内脉冲电流的变化情况如图3所示,图中T1为脉冲电流的作用时间,T2为一个周期.

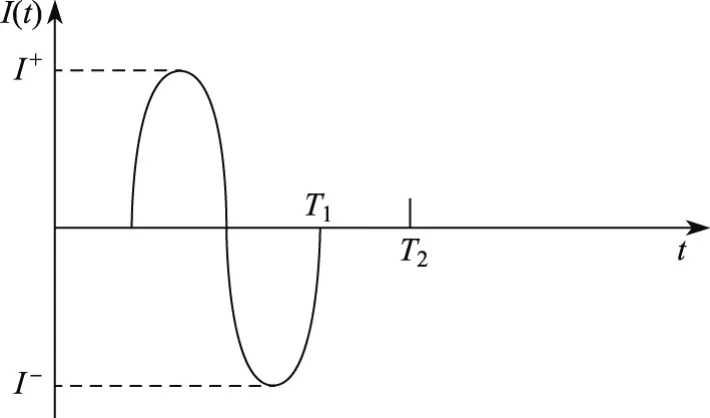
图3 脉冲电流变化Fig.3 Variations of pulse current

对于磁感应强度,由于只考虑一个脉冲周期,故分别取T1/4,T1/2,3T1/4,T1和T2时刻的铸坯熔体内磁感应强度,其分布情况如图4所示.从磁感应强度随时间变化的规律来看,时间不同磁感应强度的方向也不同,磁感应强度的分布显示出脉冲电磁场传播具有一定的趋肤效应,即越靠近铸坯内部,磁感应强度越小.

4.3 电磁力的分布

考虑到脉冲电流具有周期性,故只研究一个周期内的电磁力分布情况.电磁力是感应电流和磁感应强度的矢积,由于感应电流与磁感应强度存在一定的相位差,因此分别取T1/8,T1/4,3T1/8,T1/2,5T1/8,3T1/4,7T1/8和T1时刻的铸坯熔体电磁力分布(见图5).从图5可以看出,电磁力主要集中在铸坯表面趋肤深度内,其方向随着脉冲电流的变化而变化;随着脉冲电流向铸坯熔体内部传播,电磁力逐渐衰减.

4.4 焦耳热分布

不同时刻铸坯内部焦耳热的分布如图6所示.从图中可以看出,焦耳热的分布同样与电磁场的趋肤效应有关,其分布随着时间的变化而变化;不同时刻焦耳热的分布范围不同,主要分布在铸坯的趋肤深度内.焦耳热的产生相当于为铸坯提供了一个内热源,使铸坯内部的冷却速率降低,延长了铸坯表面形成凝固坯壳的时间,改变了铸坯内部温度场的分布.

4.5 流场分布

在未施加PMO作用时,铸坯内部流场分布如图7(a)所示.图中,钢液由水口浇入结晶器中,在重力作用下钢水向下流动,由于钢液从水口流出速度大于拉速,因此在结晶器中有一部分钢水回流;当铸坯继续向下移动,钢液的流动方向为垂直向下(见图7(b)).当在足辊段下端施加PMO作用时,由于加载了变化的电磁力场,故铸坯内部靠近线圈位置形成上下两个回流区(见图7(c)和(d)所示).

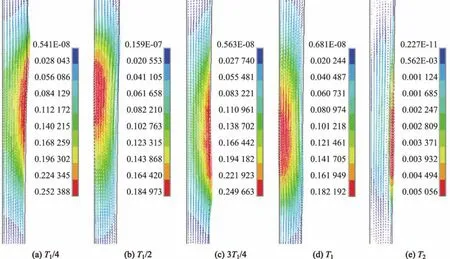
图4 不同时刻铸坯内部磁感应强度的分布(T)Fig.4 Distributions of the billet internal magnetic f l ux density at diあerent time(T)

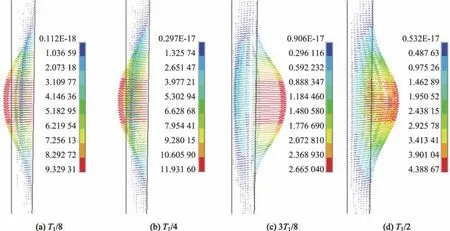
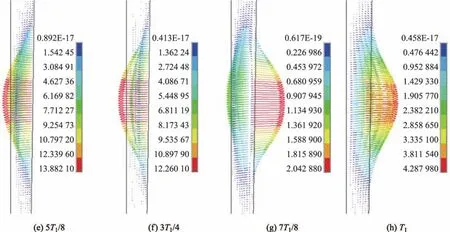
图5 不同时刻铸坯内部电磁力的分布((T.A2)/kg)Fig.5 Distributions of billet internal electromagnetic forces at diあerent time((T.A2)/kg)

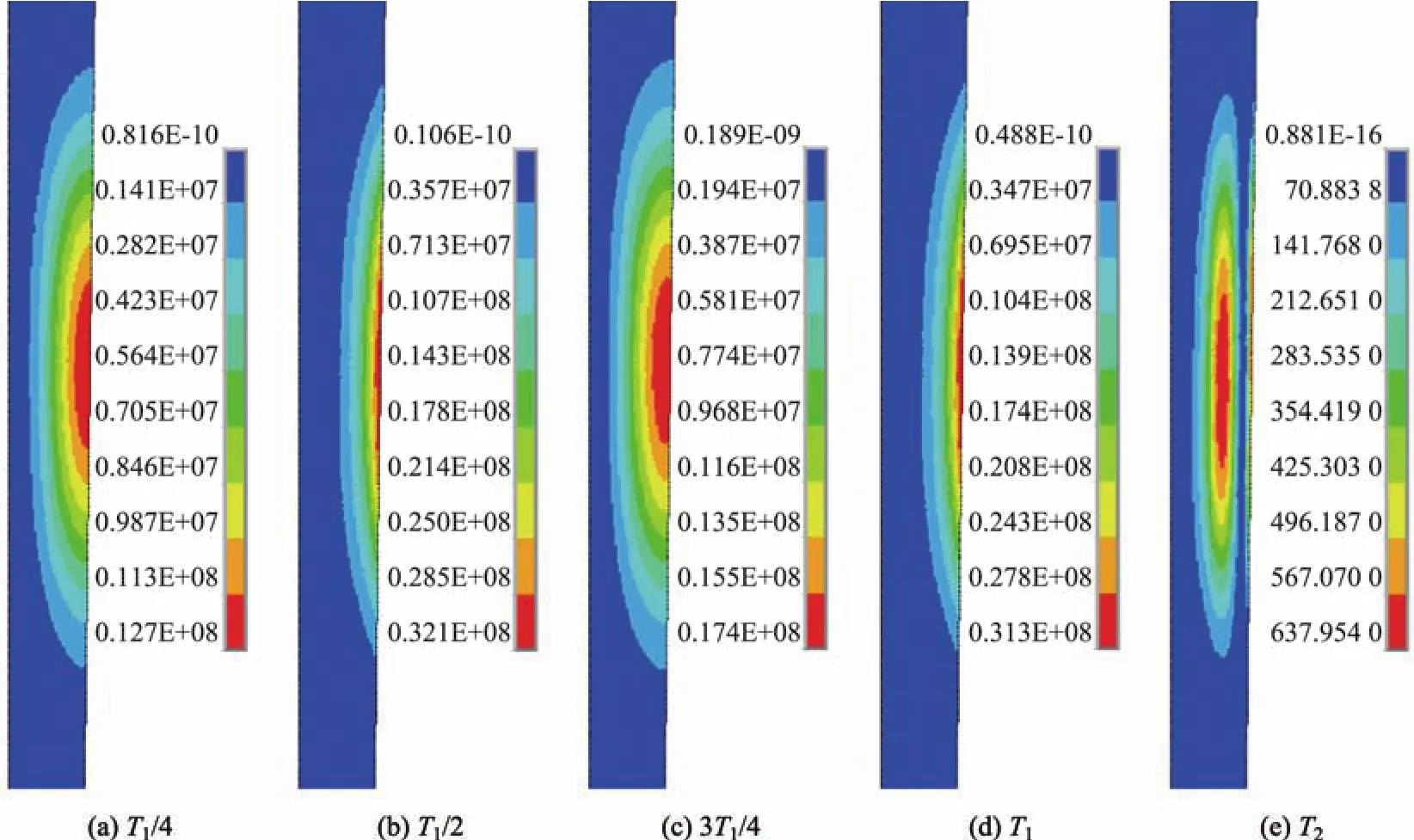
图6不同时刻铸坯内部焦耳热的分布(A2/(s.m3))Fig.6 Distributions of the billet internal Joule heat at diあerent time(A2/(s.m3))

4.6 温度场分布

图8 为铸坯内部温度分布图.图8(a)和(c)为未施加/施加PMO作用时铸坯内部温度分布,(a)中过热钢水从水口流出,受重力作用向下流动,在靠近中心位置温度较高,在靠近铸坯表面的位置温度迅速下降.从图7(b)和(d)对比中可以看出,由于电磁力的驱动,铸坯内部钢水旋转形成回流,故钢水温度在拉坯方向迅速降低,热区位置上移,铸坯轴向温度梯度降低,径向温度升高.

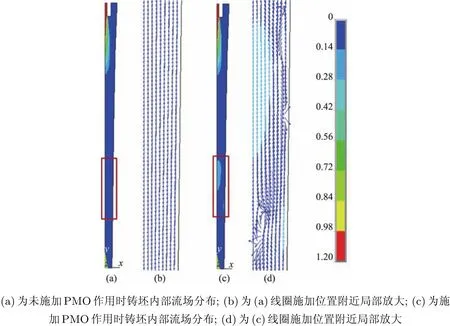
图7 铸坯内部流场分布(m/s)Fig.7 Distributions of the billet internal f l ow f i eld(m/s)

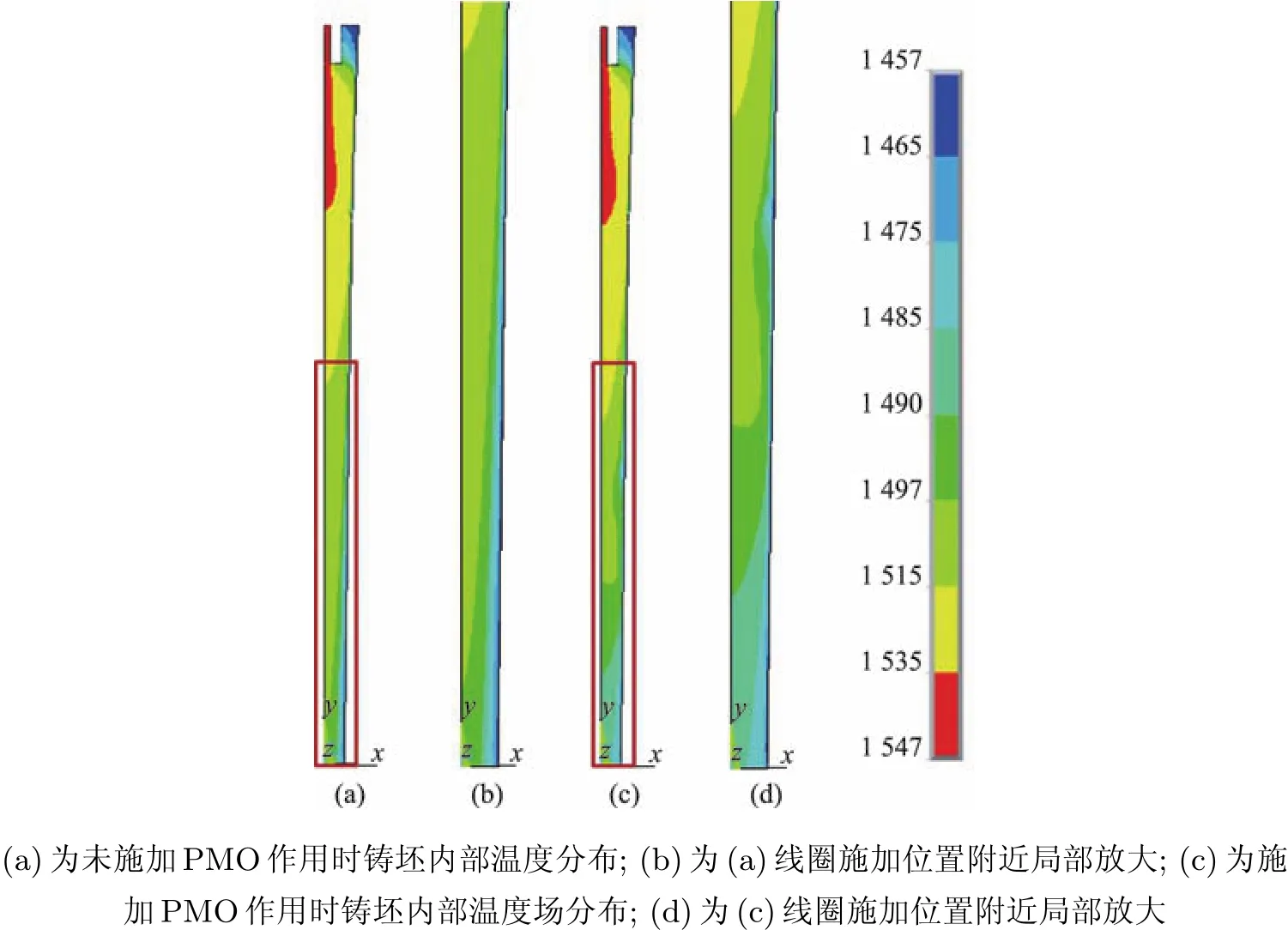
图8 铸坯内部温度分布(°C)Fig.8 Distributions of the billet internal temperature f i eld(°C)

为研究PMO作用对铸坯内部温度场的影响,分别取线圈起始端、中间段及末端PMO未处理/处理的铸坯径向温度进行比较(见图9).在线圈起始端,由于电磁力作用形成回流,故流速方向是由铸坯表面向中心流动,导致表面相对温度较低的钢液流向中心相对温度较高的钢液,使得靠近中心的钢液温度降低.而线圈中间段和末端由于回流中流速方向由铸坯中心向表面流动,铸坯轴向温度梯度降低,使得铸坯内部的温度场分布更加均匀.

在PMO作用下,铸坯内部的磁场、电磁力都呈现出时间上波动和空间上分布不均匀的状态,这将增加电磁场作用区域的能量起伏,成为一种从热力学上促进形核的因素.此外,在电磁力作用下铸坯内部会形成上下两个回流区,不同位置的流速方向不同,靠近坯壳处的流动能够引起钢液对坯壳的不断冲刷,有利于晶核游离.另外,由于电磁作用导致的涡流会将靠近坯壳处较冷的钢液带入到中心温度相对较高的部分区域,或者将中心温度较高的钢液带入到靠近坯壳处较冷的区域,这种形式的流动能够降低铸坯中心温度,铸坯轴向温度梯度降低,有利于晶核存活.

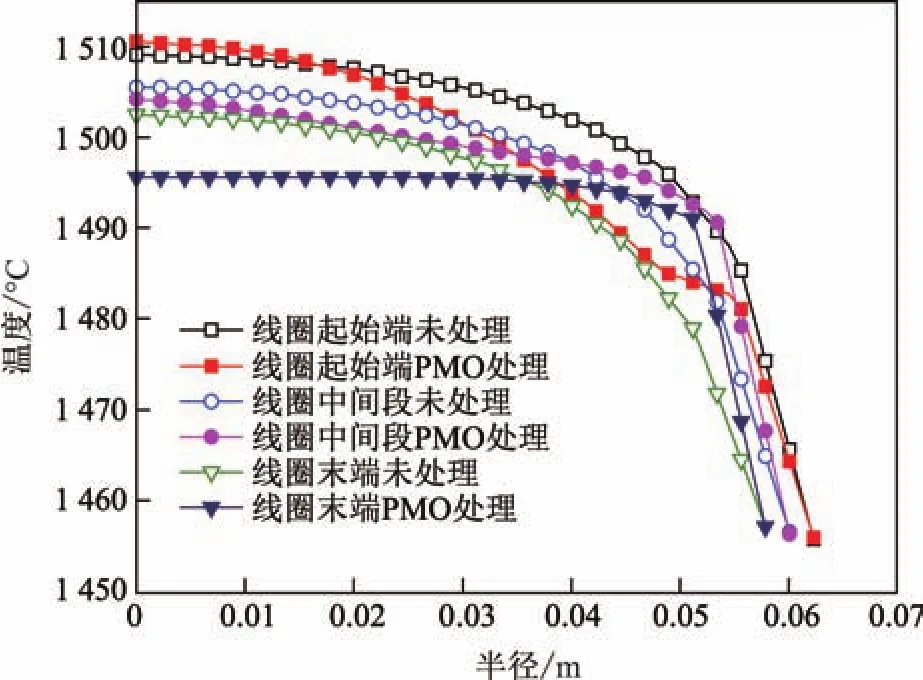
图9 线圈不同位置铸坯内部温度场分布Fig.9 Distributions of the billet internal temperature f i elds in diあerent positions of the coil

5 结论

(1)利用薄片移动法计算得到施加PMO位置的坯壳厚度为27 mm,工厂实测施加PMO位置的坯壳厚度为27.9 mm,误差率为3.22%;

(2)电磁场主要分布在铸坯的趋肤深度内,其分布随着时间的变化而变化,并且越靠近铸坯内部磁感应强度和电磁力越小;

(3)当铸坯中施加脉冲磁致振荡作用时,由于加载了不均匀的电磁力场,铸坯内部靠近线圈位置的钢液将形成上下2个回流区;

(4)由于电磁力的驱动,铸坯内部钢水形成回流,从而使得钢水的温度在拉坯方向降低,铸坯轴向温度梯度降低,有利于晶核存活.

[1]VIVES C,RICOU R.Experimental study of continuous electromagnetic casting of aluminum alloys[J].Metallurgical and Materials Transactions B,1985,16(2):377-384.

[2]LANGENBERG F C,PESTEL G,HONEYCUTT C R.Grain ref i nement of steel ingots by solidif ication in a moving electromagnetic f i eld[J].Trans Metall Soc AIME,1961,221:993-1000.

[3]VIV`ES C.Eあects of electromagnetic vibrations on the microstructure of continuously cast aluminium alloys[J].Materials Science and Engineering A,1993,173(1/2):169-172.

[4]葛丰德.电磁场对铝合金凝固过程的影响[J].哈尔滨理工大学学报,1983(1):70-78.

[5]ZHAI Q J,LI Q S,LI H B.Structure evolution and solidif i cation behavior of austenitic stainless steel in pulsed magnetic f i eld[J].Journal of Iron and Steel Research International,2006,13(5):69-72.

[6]GONG Y Y,LUO J,JING J X,et al.Structure ref i nement of pure aluminum by pulse magnetooscillation[J].Materials Science and Engineering A,2008,497(1):147-152.

[7]LIAO X,ZHAI Q,LUO J,et al.Ref i ning mechanism of the electric current pulse on the solidif ication structure of pure aluminum[J].Acta Materialia,2007,55(9):3103-3109.

[8]黄军涛,赫冀成.方坯连铸二冷区电磁旋转搅拌数值模拟[J].钢铁研究学报,2001,13(5):19-23.

[9]于海岐,朱苗勇.圆坯结晶器电磁搅拌过程三维流场与温度场数值模拟[J].金属学报,2008,44(12):1465-1473.

[10]陈伟,王宝祥,冯永平,等.φ210 mm圆坯结晶器电磁场-流场-温度场耦合数值模拟研究[J].铸造技术,2013(4):458-461.

[11]翟启杰,龚永勇,李仁兴.脉冲磁致振荡凝固细晶技术及其在连铸中的应用[C]//炼钢品种、质量提升研讨会.2015:12-16.

[12]NOZAKI T,MATSUNO J I,MURATA K,et al.A secondary cooling pattern for preventing surface cracks of continuous casting slab[J].Trans Iron Steel Inst Jpn,1978,18(6):330-338.