发动机爆震室气液两相爆轰性质

王晨辰,翁培奋,丁 珏,李家骅,陈永杰

(上海大学上海市应用数学和力学研究所,上海200072)

脉冲爆震发动机是一种基于爆轰燃烧的新概念推进系统,其中爆震室内气液两相爆轰是发动机产生推力的重要过程,影响着发动机的动力和热力性能.

燃料颗粒散布在空气或氧气中会形成可燃的混合介质,点燃该系统会发生两相爆轰.1978年,Gabrijel等[1]研究了在楔形激波管中平均直径为388µm的煤油液滴与空气混合物形成的云团的爆轰.此后Dabora[2]建立了初步的理论模型来描述两相爆轰,模型中采用了较多的经验公式和假设.随着计算流体力学的发展,数值模拟逐渐成为研究两相系统爆轰的一种重要手段,其中Eulerian-Eulerian模拟方法应用较为广泛.1999年中国工程物理研究院的洪滔等[3]利用一维双流体模型对正庚烷、铝粉颗粒在空气、氧气中的爆轰现象进行了研究,得出了燃料空气比、指前因子及液滴半径等因素对爆轰参数的影响;上海大学的丁珏等[4]分析了在双流体模型下,两相爆轰时压力的最大上升速率以及气相体积分数对爆轰波压力的影响;南京理工大学的马丹花等[5]在一维和二维双流体模型的基础上,发展了时空守恒元和解元(space-time conservation element and solution element,CE/SE)方法,较好地对爆轰波进行了研究.由于Eulerian-Eulerian方法对离散相无法较为准确地描述颗粒动力学过程,因此研究者利用Eulerian-Lagrangian模型开展对气液、气固两相爆轰的研究.许厚谦等[6]模拟了激波点燃粉尘颗粒的一维非定常两相化学反应爆轰模型;Cheatham等[7]对JP-10燃料爆轰进行了数值模拟研究,分析燃料液滴粒径对爆轰压力及爆速的影响;蒋弢等[8]对汽油液滴的爆轰情况进行了数值模拟,分析起爆距离与粒径之间的关系.

两相爆轰过程涉及液体燃料在前导激波及其气流作用下变形、破碎、蒸发及化学反应等多个复杂过程.为了揭示爆轰波与颗粒动力学的作用机制,分析爆轰波参数与燃料液滴粒径的关系,本工作开展了爆震室气液两相爆轰过程和颗粒动力学特性的数值研究,为推动爆震推进技术的应用奠定基础.

1 气液两相燃烧爆轰反应模型

1.1 气相控制方程

爆轰是个非定常的过程.

(1)气相控制方程

连续方程:

动量方程:

能量方程:

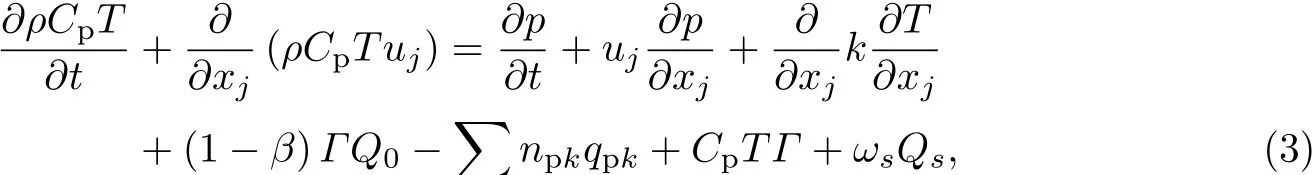
组分输运方程:

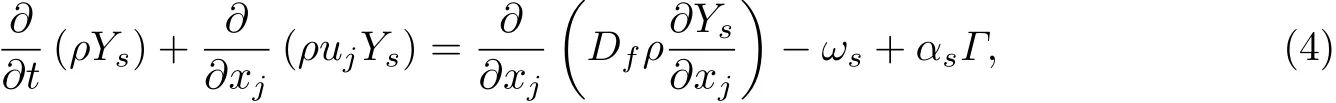
(2)颗粒相控制方程

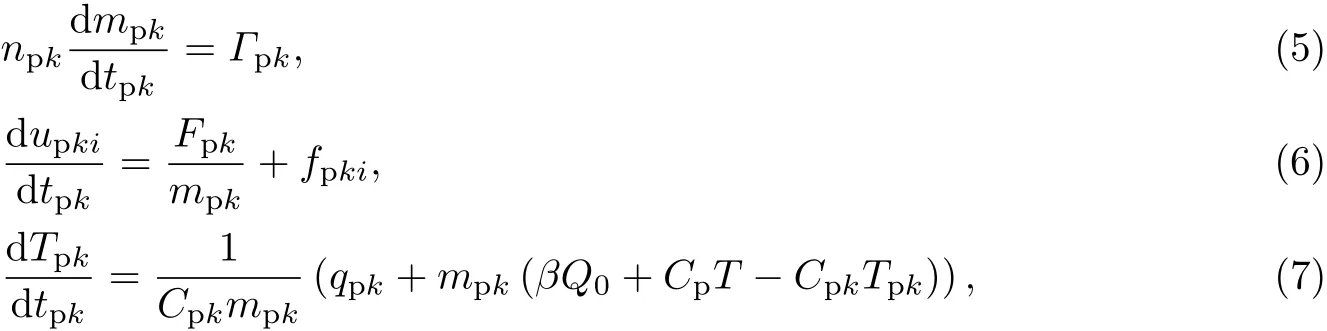
式中,下标p为液滴;k为第k相组分;为液滴组分k的质量变化率;npk为颗粒数密度,即单位体积内k相颗粒的个数;Fpk为单个液滴所受的力;fpk为场力及其他诸力;qpk为单个液滴从气相获得的热;β为分配因子,表示液滴释放的热在两相间的分配;Q0为单位质量的液滴燃烧释放的热;Qs为气相组分s的反应热;ωs为反应速率;Df为质量扩散系数;Ys为该组分在气相中的质量分数;αs为液滴蒸发产物中组分s的质量分数.

此外,气相遵守理想气体状态方程:

式中,Ws为气相组分s的物质的量.

1.2 化学反应模型

为了提高计算效率,采用一步总包化学反应模型:

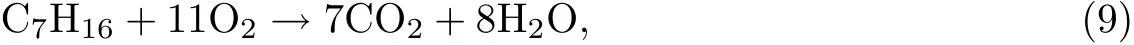
假定燃烧速度ωr受指前因子A、氧气浓度CO2、庚烷气体浓度CC7H16及活化能Ea的影响,利用Westbrook等[9]的一步反应描述化学反应过程,有

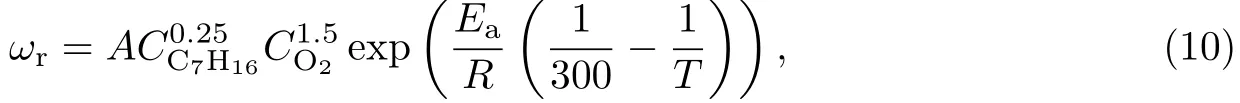
式中,R为普适气体常数,指前因子A及活化能Ea的值引自Westbrook等[10]的文献.

燃烧模型采用部分搅拌反应器(partially stirred reactor,PaSR)模型[11-12]来考虑湍流效应的影响.PaSR模型引入了化学反应时间尺度τchem和混合时间尺度τmix,认为在τchem时间内组分基于化学反应速率ωr反应的产生/消耗量,与在(τchem+τmix)时间内以实际化学反应速率反应的产生/消耗量相同.因此,实际的化学反应速率为

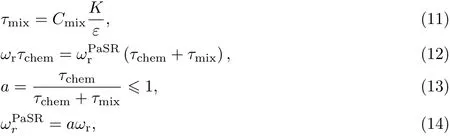
式中,K为湍动能,ε为湍动能耗散率,Cmix为常数.各算例中,混合的时间尺度就是湍流时间尺度,因此Cmix取1.

1.3 数值格式

压力与速度的耦合采用改进版的simple算法——pimple法,压力场与速度场分别存放在2套不同的网格中,故压力求解器选用的是代数多重网格求解器(geometric and algebraic multigrid,GAMG).在插值格式方面,时间的离散采用1阶隐式Euler形式,梯度格式采用高斯线性插值,扩散相采用2阶高斯守恒格式,表面插值采用中心差分格式.关于对流相的选择,由于需要对爆震波进行捕捉,总变差减小(total variation diminishing,TVD)差分格式具有分辨率高、间断面处无非物理振荡、光滑区域精度高等优点,而具有TVD性质的MUSCL(monotonic upwind scheme for conservation law)格式[13]采用一种保持光滑解高阶精度的通量限制器,抑制间断附近的数值解波动,且在解的光滑区域内具有2阶精度,因此是一类高分辨率捕捉激波格式.本工作的对流相采用MUSCL差分格式,由于运用拉格朗日法追踪,故对于燃料液滴采用Euler形式对时间进行积分.

2 气液两相爆轰的数值模拟

图1为计算区域,点火采取高温高压区域,该区域长1.00 m,高0.06 m,上、下和左侧为固壁,右侧为出口.流场内部压力初始值为一个大气压,温度为300 K.为使燃料氧气按照等当量比进行化学反应,内部均匀预混分布着9.38×104个正庚烷液滴(化学式为C7H16,密度ρ=675 kg/m3).为便于计算,将计算域划分为1 000×60个矩形网格.

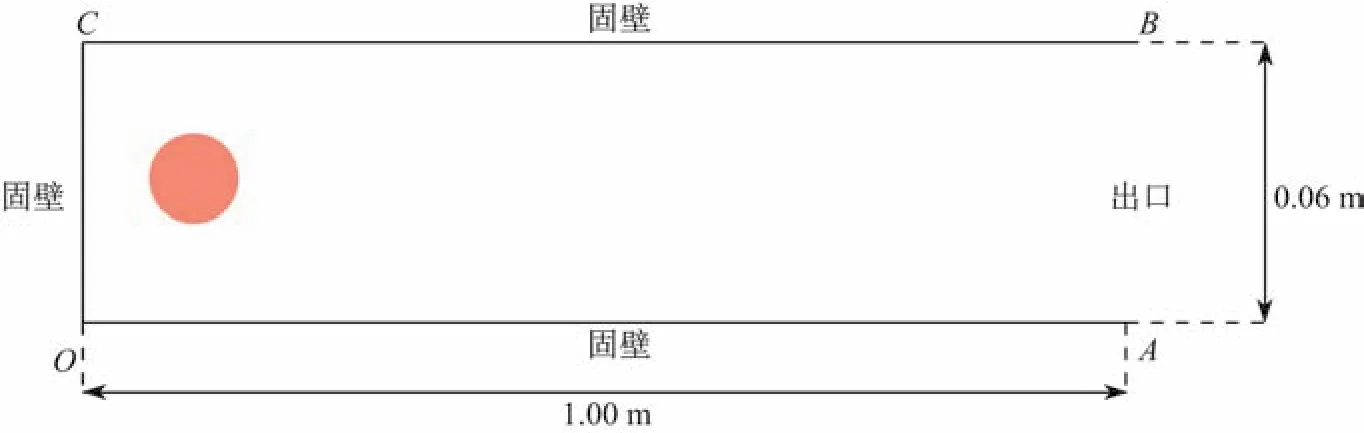
图1 计算区域Fig.1 Computed f i eld

2.1 空气-燃料两相系统的爆轰性质

为验证计算模型,将本工作中模拟得到的爆轰波压力与文献[8]的实验结果进行对比(见图2).图2中实线为实验测得的汽油/空气(汽油的主要成分为正庚烷)爆轰波压力随时间演化图.文中计算的正庚烷与空气混合物爆轰压力曲线如图2的虚线所示.可以看出,MUSCL格式能够较为准确地捕捉激波,对激波的分辨率是很高的.

相比较而言,数值计算结果与实验结果波形基本一致,均呈现出在爆轰波到达后流场压力值先急剧上升,随后再逐渐下降的现象.计算得到的压力峰值为3.396 7 MPa,比实验结果高出约0.5 MPa.偏差的原因主要是本工作中燃料为纯庚烷,单位时间、单位体积内释放的热量更多.

为了验证网格的无相关性,将网格数增加至1 500×90和2 000×120,得到的压强峰值分别为3.408 7 MPa和3.412 5 MPa,相差仅为3.5%和4.7%,因而可以认为当网格数大于6×104后,计算结果受网格数量的影响不大.

(1)爆轰的C-J状态.

根据ZND(von Zeldorich Neumann-Doering)模型,爆轰波由前导激波和反应区构成,反应区的末端平面称为C-J面,反应区止于C-J面,该处气相状态被称为C-J状态.现将由较小粒径的燃料液滴(25µm)组成的系统进行具体的分析.

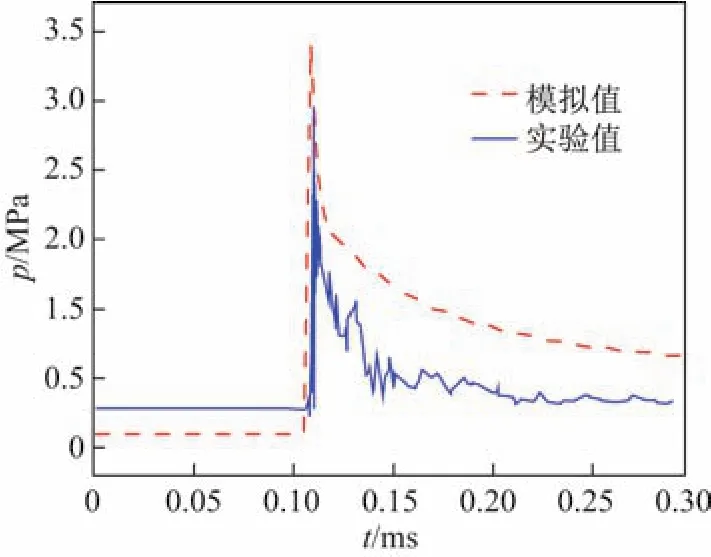
图2 数值模拟与实验对比Fig.2 Comparison of numerical simulation and experimental data

图3爆轰过程中的C-J状态Fig.3 C-J state in detonation process

图3 (a)为计算不同时刻爆轰场H点的p-v(压力比体积)关系图,其中各点表示在爆轰波经过前后,流场H点处气体的状态参数.如果将火焰前后气体参数与释放热量Δq的关系式称为Hugoniot方程,则由Δq值得到的一簇曲线称为Hugoniot曲线簇.图中,实线所连的点构成了Δq=0的Hugoniot曲线,亦称为Hugoniot激波曲线,表示尚未反应的阶段;标记点构成的曲线上Δq=1,被称为Hugoniot产物曲线,表示反应完毕后的阶段.以气相参数初始状态点O为原点,过该点作Hugoniot爆轰产物曲线的切线,则与Hugoniot曲线的切点(H点)被称为爆轰的C-J状态点,表示恰好进入稳定爆轰状态.切线称为Rayleigh线,即爆轰波的波速线.

将C-J状态标记于所对应的压力p、速度u及密度ρ曲线中(见图3(b)～(d)).可以看到,C-J状态H点位于曲线的鞍点处.通过将C-J状态参数与文献[14]中C-J理论值的对比(见表1)可以看出,小粒径的燃料液滴(25µm),计算出的C-J状态对应的爆轰参数与理论值较接近,验证了本工作中建立的模型和研究方法是可行的.

表1 正庚烷/空气爆轰参数Table 1 Detonation parameters of n-heptane/air mixture

(2)爆轰波的传播过程.

图4为半径为25µm的正庚烷液滴与空气混合发生两相爆轰时,爆轰波在x方向传播时的压力、密度曲线.通过计算可知,稳定后的爆轰波传播速度约为1 720 m/s.

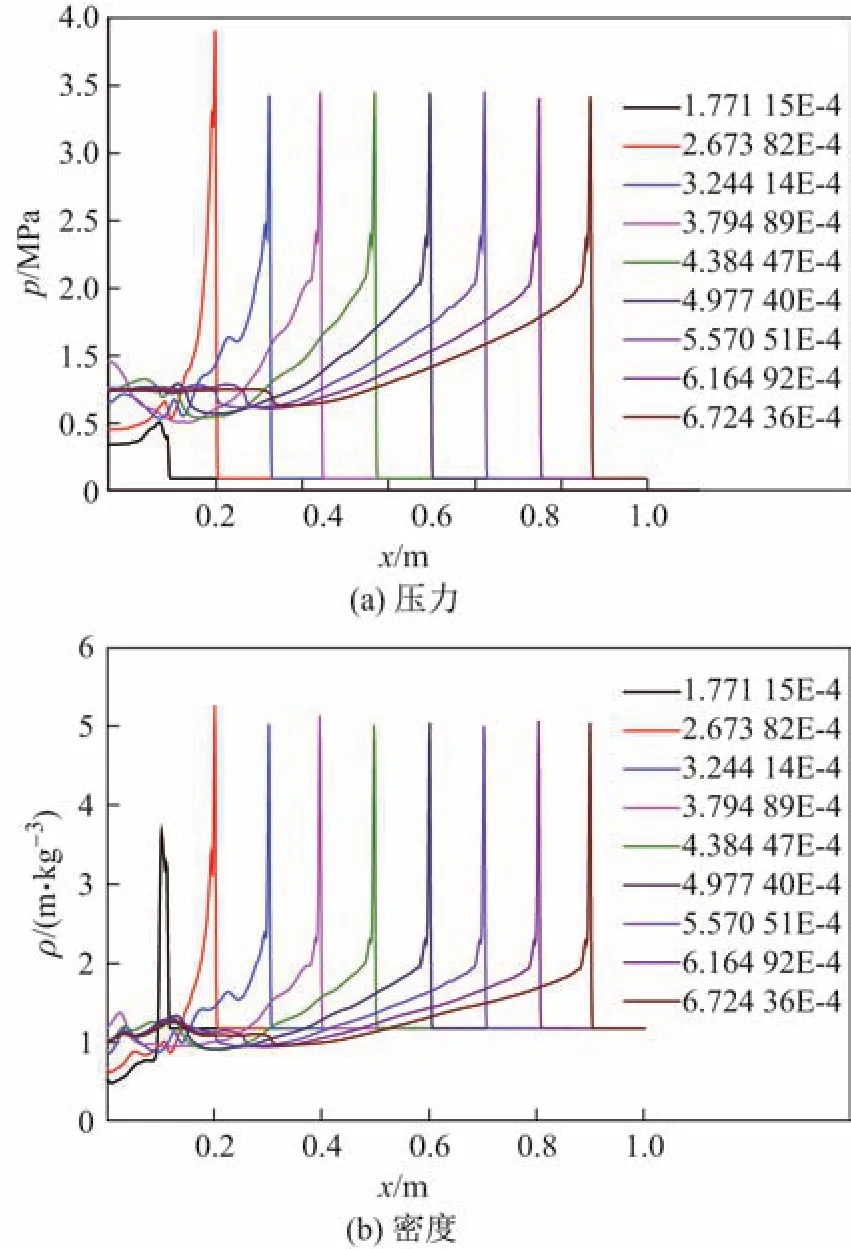
图4 轴线上爆轰波压力、密度随时间的演化Fig.4 Evolution of detonation pressure and density along axis

2.2 氧气-燃料两相系统的爆轰性质

2.2.1 爆轰波后颗粒蒸发域宽度的分析

两相系统的爆轰波是由前导激波和激波后的化学反应区组成,其中爆轰波后燃料液滴的破碎、蒸发时间和宽度决定了反应区中能量的释放速率.

图5为激波到达距离爆震管封闭端0.6 m位置时该处燃料液滴粒径的分布情况.横轴坐标为爆震管轴线位置,纵轴坐标代表液滴的直径.从图5中可以看出,虽然燃料初始粒径不同,但是在破碎蒸发等动力学过程中粒径变化却相似.将液滴从开始相变到结束的宽度Δx定义为液滴破碎蒸发域宽度.对于初始粒径为25µm的正庚烷液滴,其爆轰波后颗粒破碎蒸发域宽度Δx=0.010 96 m,此后均相变为气相的庚烷;而对于初始粒径为50,75和100µm的液滴,破碎蒸发域宽度则分别为0.022 81,0.032 29和0.041 21 m.

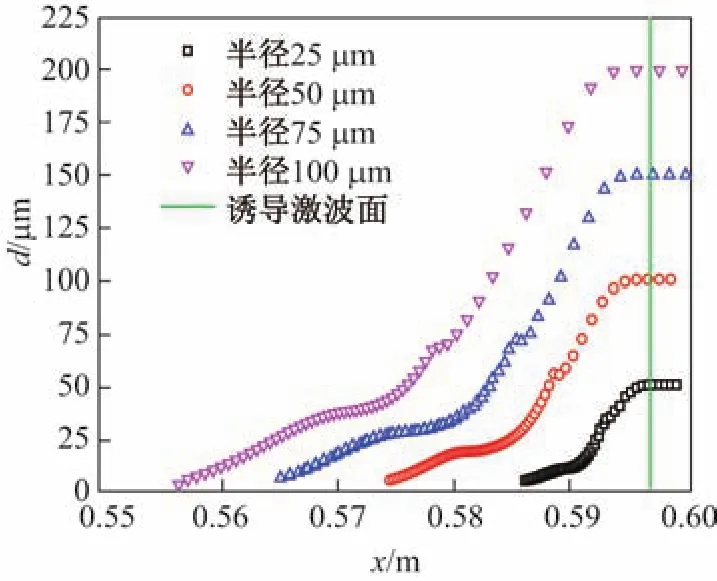
图5爆轰波后粒径分布Fig.5 Droplet size distribution behind detonation wave front

图6 为计算所得的液滴初始半径与破碎蒸发域宽度.图中,黑点为计算所得的液滴初始半径与破碎蒸发域宽度,红线为拟合曲线.通过拟合分析可知,拟合函数满足直线变化关系,说明了在本工作讨论的范围内,随着粒径的增大,液滴破碎蒸发域宽度增大;液滴破碎蒸发域宽度为粒径的函数,二者存在线性关系.

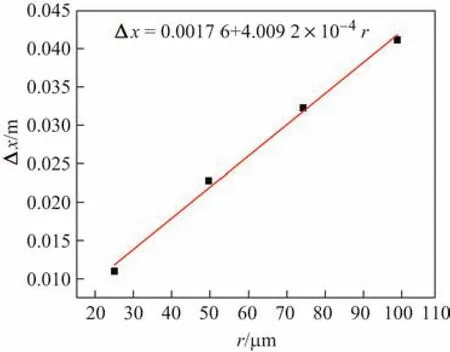
图6 颗粒初始半径与破碎蒸发域宽度Fig.6 Initial droplet size and width of break and evaporation region

2.2.2 燃料液滴的初始粒径对爆轰压力的影响

图7为当两相反应的化学当量比为1时,不同粒径的庚烷液滴在氧气中爆轰的压力分布情况.图中虚线为文献[3]数值计算值.从图中可以看出,随着粒径的增大波形的宽度不断增大,而爆轰的压力峰值逐渐降低.这是因为较大粒径的庚烷液滴的破碎和蒸发的特征时间较长,使得反应速率降低,导致爆轰波压力峰值也随之减小.

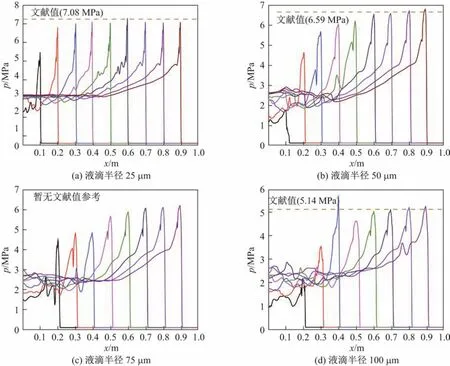
图7 氧气中爆轰时轴线压力随时间变化Fig.7 Time variations of the pressure along the axis while detonation happened in oxygen

当气液相化学当量比为1时,不同粒径庚烷液滴在氧气中爆轰的相关参数如表2所示.

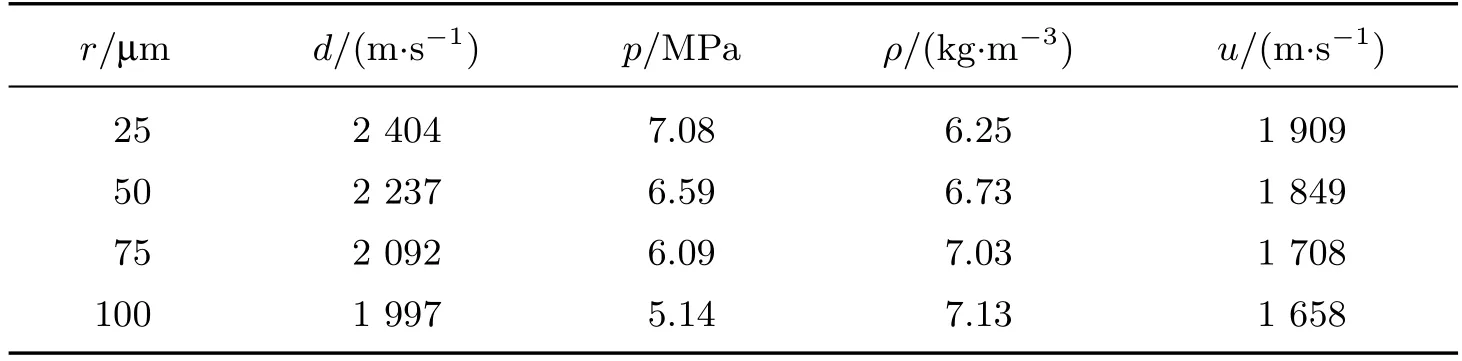
表2 氧气中两相爆轰参数与粒径关系Table 2 Relations between detonation parameters and droplet sizes in oxygen

2.2.3 流场组分的分布及反应区宽度

爆轰波经过x=0.6 m时,液滴在不同初始粒径下流场化学反应组分体积分数的分布如图8所示.从图中爆轰波后化学反应区宽度与液滴半径的关系可看出,液滴的粒径越大,反应区宽度也越大.

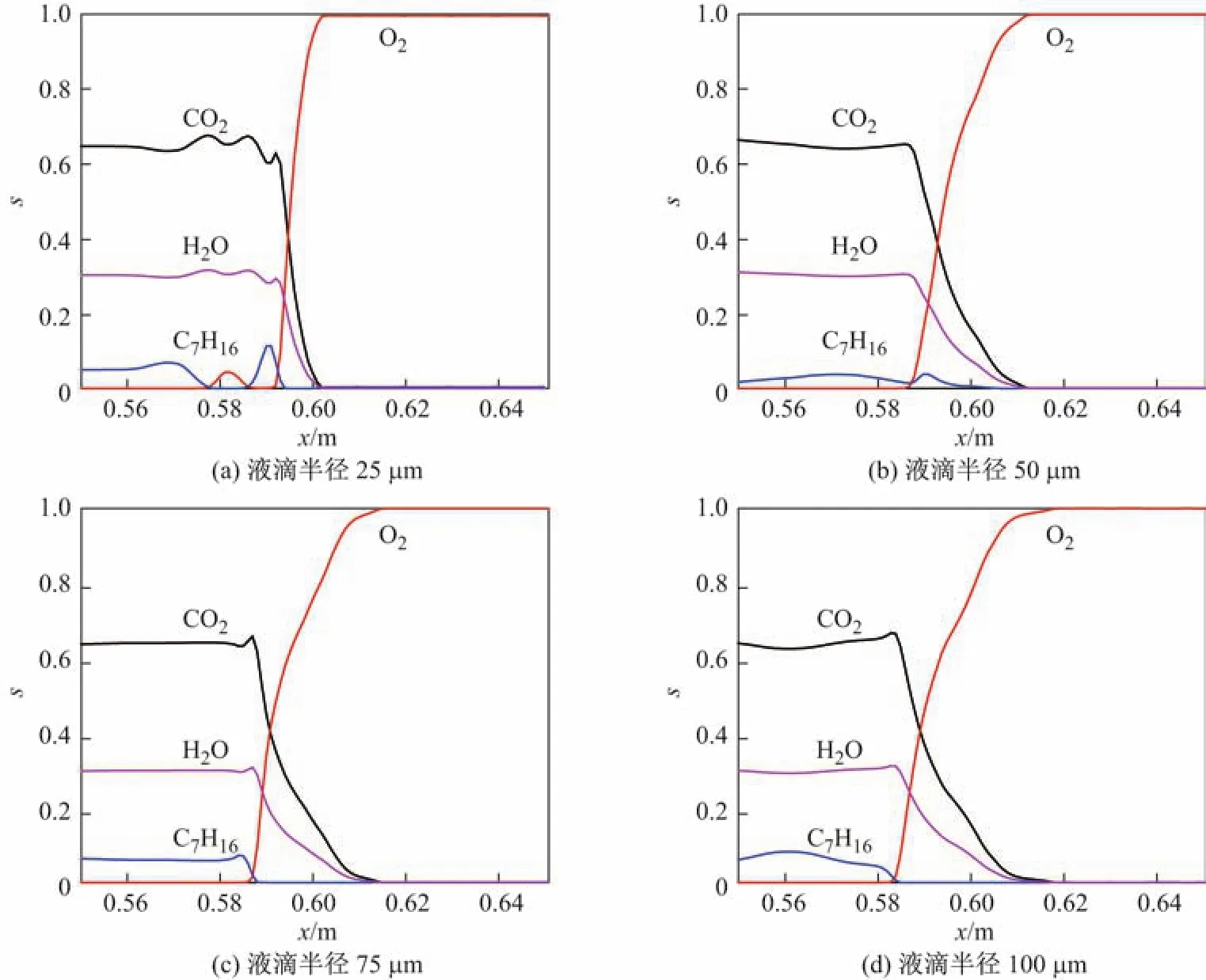
图8 爆轰反应气体组分体积分数的分布Fig.8 Distributions of detonation species volume fraction

3 结论

气液两相爆轰是含化学反应的多相流体力学过程.本工作重点研究两相爆轰波性质,以及液滴初始粒径对爆轰波结构的影响.

(1)数值分析两相爆轰的热力学过程.对于空气-庚烷燃料两相系统的爆轰,计算爆轰场H点的p-v图,得到Hugoniot曲线和Rayleigh曲线.对于初始粒径为25µm的燃料液滴,计算所得到的在C-J状态下爆轰压力、密度、气流速度、爆轰波传播速度分别为1.802 2 MPa,2.161 3 kg/m3,721 kg/m3和1 720 m/s,与理论值接近,验证了本工作中建立的模型和研究方法的正确性.

(2)进行两相爆轰过程的数值研究.燃料液滴在前导激波及在气流作用下会发生破碎、蒸发及化学反应的动力学过程.基于此,本工作中数值分析了液滴初始粒径对其破碎蒸发域宽度、爆轰波反应区宽度的影响.研究结果发现,在均匀预混的爆轰下,燃料液滴初始粒径越大,液滴蒸发、反应区宽度越大,爆轰波压力峰值越小,液滴破碎蒸发域的宽度是初始粒径的函数.

[1]GABRIjEL Z,NICHOLLS J A.Cylindrical heterogeneous detonation waves[J].Acta Astronautica,1978,5:1051-1061.

[2]DABORA E K.A model for spray detonation[J].Acta Astronautica,1978,6:269-280.

[3]洪滔,秦承森.气体-燃料液滴两相系统爆轰的数值模拟[J].爆炸与冲击,1999,19(4):336-342.

[4]丁珏,应梦侃.基于两相流模型数值研究可燃颗粒燃烧爆轰的特性[J].中国安全生产科学技术,2014,10(3):17-20.

[5]马丹花,翁春生.二相湍流爆轰流场的数值仿真[J].计算机仿真,2012,29(6):85-88.

[6]许厚谦,于强.激波点燃粉尘的数值模拟研究[J].爆炸与冲击,1994,14(4):290-297.

[7]CHEATHAM S,KAILASANATH K.Multi-phase detonations in pulse detonation engines[C]//AIAA Aerospace Sciences Meeting and Exhibit.2006.

[8]蒋弢,翁春生.气液两相脉冲爆轰发动机的建模和仿真[J].计算机仿真,2012,29(8):77-80.

[9]WESTBROOK C K,DRYER F L.Simplif i ed reaction mechanisms for the oxidation of hydrocarbon[J].Combustion Science and Technology,1981,27:31-43.

[10]WESTBROOK C K,DRYER F L.Simplif i ed reaction mechanisms for the oxidation of hydrocarbon fuels in f l ames[J].Combustion Science and Technology,1981,27:31-43.

[11]GOLOVITCHEV V I,CHOMIAK J.Evaluation of ignition improvers for methane auto-ignition[J].Combustion Science and Technology,1998,135:31-47.

[12]GOLOVITCHEV V I,NORDIN N,CHOMIAK J.Numerical modeling of hydrogen def l agration in multi-room compartments[J].Proceedings of the Computational Technologies for Fluid/Thermal/Chemical Systems with Industrial Applications,1998,377(2):169-176.

[13]VAN LEER B.Towards the ultimate conservative diあerence scheme.V.a second-order sequel to Godunov’s method[J].Journal of Computational Physics,1979,32(1):101-136.

[14]洪滔.两相爆轰的理论和数值研究[D].绵阳:中国工程物理研究院,2004:38-39.本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn