社会网络影响力最大化的核重构算法及传播模型

刘钰峰 郅欢欢 周喻鑫(湖南大学信息科学与工程学院 湖南 长沙 410082)

0 引 言

近年来，大规模社会网络(如facebook、新浪微博、人人网等)迅速发展，这为“口碑”与“病毒营销”提供了机遇，随之也产生了一个关键的问题，即如何从大规模的社会网络中挖掘一些节点，并使这些节点在网络中传播影响最大化[1-4]。

在社会网络中，判断初始节点的影响力需要借助相应的传播模型。独立级联传播模型IC(Independent Cascade Model)和线性阈值传播模型LT(Linear Threshold Model)是最基本的传播模型，除此之外，在社会网络传播过程中通用的信息传播模型还有SI、SIR、SIS[5-7]等。Gopalan等[8]提出SI信息传播模型在社交网络中运用广泛，且效果比较好。Zhang等[9]经过对社会网络结构分析，根据节点的度将节点进行分类，提出了改进的SI信息传播模型。Xu等[10]接着提出了SIS的信息传播模型。Hacid等[11]基于SIR信息传播模型和SIS信息传播模型进行影响力的传播预测。本文针对SI信息传播模型未考虑节点间亲密关系对信息传播的影响，提出了一种ESI信息传播模型。

社会网络节点影响力最大化问题的研究由来已久，Richardson等[12]最先将社会网络节点影响力最大化作为一个算法问题提出，选取特定初始节点使影响力最大化。之后，相关研究者[13-23]先后提出了不同的算法来解决社会网络节点影响最大化问题。Kempe等提出了贪心爬山算法[16]，影响结果达到最优解的63%。但该算法运算量大且时间复杂度较高，不适用于大型网络。Goyal[17]等对贪心算法改进后提出了一种影响最大化算法Celf++。Chen等[18]提出了一种启发式算法DegreeDiscount，当一个节点被选为初始节点后，那么计算这个节点的邻居节点的度时就打一定的折扣。Kitsak[19]等提出了一种基于覆盖的最大核算法和最大度算法。Zhou等[20]基于节点的位置特征提出了一种效率较高的影响最大化算法。Estevez等[21]提出了SCG(Slow Crack Growth)算法，选取度大的初始节点，考虑到度大的初始节点会存在重复邻居节点，所以选取的初始节点需要尽可能的分散。曹玖新等[22]提出了基于k核的影响最大化算法CCA(Core Cover-ing Algorithm)，用一个距离因子d控制初始节点的距离。Zhou[23]基于SI信息传播模型，利用社团划分来选择影响最大化的节点(本文称之为MSI算法)。对于影响最大化问题，许多研究者提出了时间复杂度相对较低的启发式算法，但其节点影响力效果却不如贪心算法。针对该问题，本文提出了一种影响效率高且时间复杂度较低的启发式算法CRA。

1 信息传播模型

1.1 SI信息传播模型

SI信息传播模型是最重要的社会网络信息传播模型之一，该模型认为每个节点只有两种状态：影响状态是S(i)与未影响状态I(i)，且节点只能从未影响状态向影响状态单向转变。SI传播模型基本思想如下：首先得到节点t-1时的影响状态，根据邻居节点的影响状态与已影响的邻居节点的影响概率α，得到所有邻居节点对该节点的影响概率，最后得到t时该节点的影响状态。

1.2 ESI信息传播模型

在SI信息传播模型中，节点与已影响邻居节点间的影响程度用一个常数α来进行计算，但在真实社会网络节点影响传播过程中，节点间的关系不同，被影响的程度也不同。通常两个节点之间越亲密，就会更加关注对方的消息，节点间的影响概率就会越大。比如两个相邻节点表示的用户关系比较亲密，那么其中一个用户发的消息就可能很快影响另一个用户，而对于相邻的是个几乎没有联系的用户，那么就不一定会被影响，所以在信息传播的过程中，要考虑节点间的这种影响因素。基于此，本文提出了ESI信息传播模型。

1.2.1 节点影响过程

本文引入节点间亲密度的概念表示节点间互动的亲密程度，用Ai,j表示节点i和节点j的亲密度，则节点间亲密度计算如下：

(1)

式中：Si表示该节点i的消息集合，Sj表示节点i的邻居节点j的消息集合，Zi表示节点i的邻居节点集合，用ei,j表示邻居节点j对节点i的影响概率，则其计算如下：

ei,j=cα+(1-c)Ai,ji∈Vj∈Zi

(2)

式中:假设α是节点起初可能被已影响节点影响的概率，属于[0,1]。c表示一个调和因子，属于[0,1]。

以下考虑节点被影响的过程，本文使用Pi,t表示节点t时刻被影响的概率。Pi,t主要与三个因素有关：1) 该节点的邻居节点t-1时刻到t时刻对其影响的概率；2) 该节点t-1时刻的影响概率；3) 该节点的邻居节点的影响状态。

本文使用χi,t来表示节点i在t-1时刻到t时刻未被已影响的邻居节点j影响的概率：

χi,t=((1-ei,j)pj,t-1)i∈Vj∈Zi

(3)

邻居节点j在t-1时刻未影响的概率为(1-pj,t-1)。

δi,t用来表示节点i在t-1时刻到t时刻未被邻居节点j影响的概率为：

δi,t=χi,t+(1-pj,t-1)=((1-ei,j)pj,t-1)

i∈Vj∈Zi

(4)

节点i存在的邻居节点j有多个，所以用βi,t来表示所有邻居节点j∈Zi从t-1时刻到t时刻未能影响节点i的概率为：

i∈V

(5)

相反，用φi,t来表示节点i在t-1时刻到t时刻被它的邻居节点影响的概率为：

i∈V

(6)

节点i在t-1时刻未被影响的概率为(1-pi,t-1)，节点i从t-1时刻到t时刻未被影响的概率为(1-φi,t)，所以节点t时刻被影响的概率为：

pi,t=1-(1-pi,t-1)(1-φi,t)i∈V

(7)

由式(6)代入式(7)可得：

pi,t= 1-(1-pi,t-1)(1-(1-

(8)

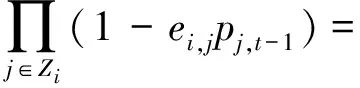
…i∈V

(9)

式(9)后面的值非常小，可忽略不计，得到：

(10)

由式(8)和式(10)得到：

(11)

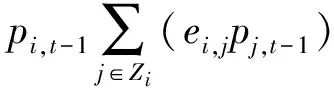
(12)

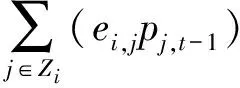
(13)

式(13)表示了一个节点从t-1到t影响概率变化的过程，也反映了节点的影响状态的变化。

1.2.2 模型框架

用向量Pt=[p1,t,p2,t,…,pn,t]表示所有节点i∈V在t时刻的影响概率，pi,t=1表示节点i在t时刻已被影响，pi,t=0表示节点i在t时刻未被影响。用矩阵E表示节点与邻居节点影响的概率矩阵，表示如下：

(14)

由传播过程得：

(15)

在t足够大时，节点的概率可能大于1，所以运用控制概率函数如下：

G([x1,x2,…,xn])= [min{x1,1},min{x2,1},…,

min{xn,1}]

(16)

将式(14)代入式(15)得到：

(17)

式(17)主要表示了ESI信息传播模型中所有节点随时间被影响的变化过程，在t=0时，初始节点的影响概率为1，通过任意时间t，可得到整个网络节点的影响状态。

社会网络影响最大化问题除了借助相应传播模型外，最重要的是初始节点的挖掘。

2 基于k阶核心集的影响最大化算法

2.1 k阶核心集

不同于曹玖新等[22]提出的k核，本文提出k阶核心集的概念。对网络中的每一个节点，其k阶核心集的定义是与之k级关联的节点集合，而k核是度值不少于k的节点推出的最大连通子图。以下是具体定义：

定义1k阶。在图G=(V,S)社交网络拓扑结构中，节点i(i∈V)会存在直接相连的节点，本文将其直接相连的节点称为第一阶节点，将它的间接节点称为第二阶节点，以此类推可以得到k阶的节点。

如图1所示一个网络节点无向图，节点1的一阶节点是4、8、21，二阶节点是2、5、7、12、13、14、16，三阶节点是9、11、15、18。当k=2时，可以得到S2(1)={4,8,21,2,5,7,12,13,14,16}。

图1 网络节点关系示意图

定义3重合率定义为节点i与邻居节点j的k阶共同节点集合与两节点k阶核心集占比，使用P(i,j)表示如下:

(18)

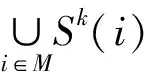
重合率的范围控制初始节点的影响状况，P太高，易局部影响最大化；P太低，初始节点k阶核心集边缘节点的连通性不好，不易被影响。所以本文提出了合适的重合率计算方法如下：

P(i,j)∈(α,β)α,β∈(0,1)

(19)

(20)

(21)

本文讨论的CRA算法主要根据节点k阶核心集初步选取，再通过重合率确定。当k为1，通过重合率范围得到的新的初始节点一般处于上一个初始节点一阶节点附近，这样得到的初始节点集没有足够的扩散，进而可能造成局部影响最大化，所以一般k从2开始选取。

2.2 CRA算法

CRA算法的基本思想简述如下：1) 根据k阶核心集，选择核心集数量大且一阶核心集不小于平均每阶核心集的节点；2) 将选择满足条件的节点进行标记，并将其一阶核心集进行标记，表示不能再被选择；3) 重合率范围判断，将新选节点与所有已选初始节点进行重合率计算。重合率的控制给各初始节点的k阶核心集边缘节点提供了多次被影响的机会。

算法1基于核重构的社会网络影响最大化算法

输入：社会网络节点G=(V,S)，节点个数N,初始节点个数m

输出：初始节点集合M

1. InitializeM=∅

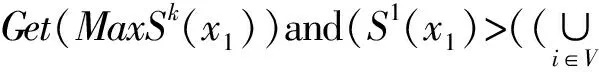
3.x1∈MAnd mark(x1,C(x1))

5. Ifx2∈(Cv(x1∪C(x1)))

6. CalculateP(x1,x2),Calculateα,Calculateβ

7. IfP(x1,x2)∈(α,β)

8.x2∈MAnd mark(x2,C(x2))

9. Else

10. markx2And Return step 4

11. End If

12. End If

该算法中的get(MaxSk(xi))表示选择出k阶核心集数量最大的节点，mark(x1,C(x1))表示选择满足条件的节点进行标记，并将其一阶核心集进行标记。Cv(x1∪C(x1))表示节点V中未标记节点。

2.3 时间复杂度分析

CRA算法节点核心集比较过程是对每一个节点的k阶核心集进行对比，故时间复杂度为O(n)；节点标记的过程是只对选择的初始节点的一阶的核心集进行标记，故时间复杂度小于O(n)；重合率计算与范围比较过程是只对选择的初始节点进行比较，所以CRA算法的时间复杂度是O(n)。

3 实验设计

3.1 数据集

本文通过新浪微博开放的API接口[24]，利用网络数据挖掘器挖掘出部分用户和对应的粉丝，以及用户转发的微博。通过爬虫程序预处理总共得到11 080个节点，1 288 045条边，以及节点在2014年8月1日到12月31日对应转发的微博消息806 854条。

3.2 实验对比

为了验证CRA算法，与其他算法进行实验对比。

对比实验算法如表1所示。

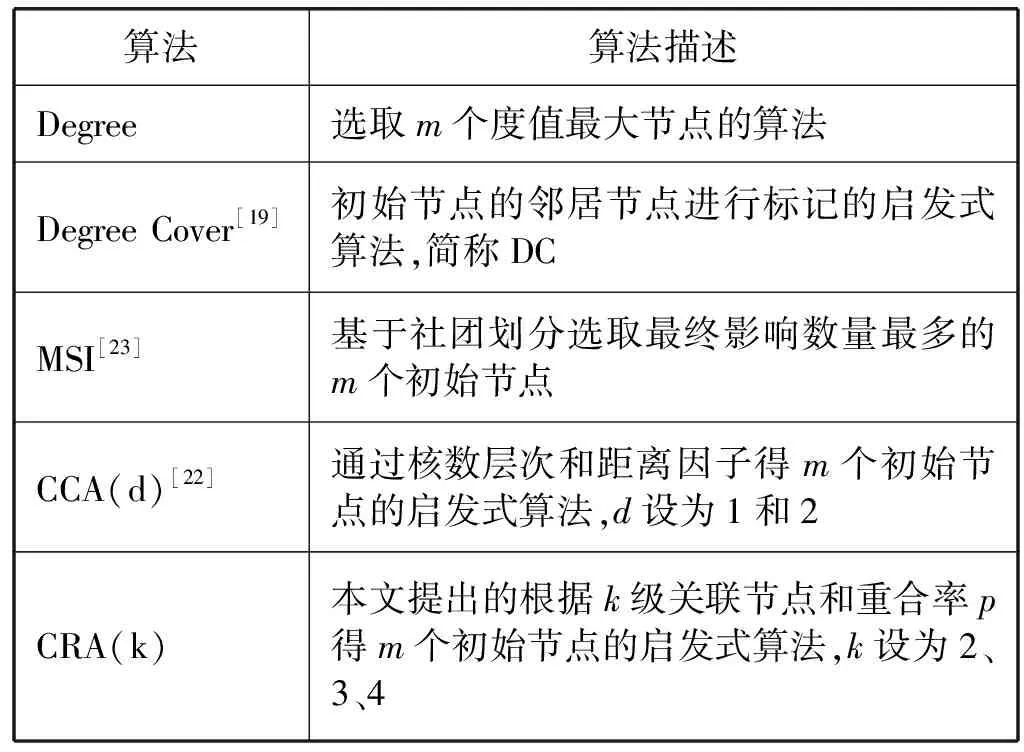
表1 对比算法

3.3 结果分析

本文的实验结果评价指标可概括为以下两点：(1) 影响范围。通过相同的时间，节点最终被影响的数量。(2) 算法的运行时间。如何用较短的时间找到初始节点。在传播影响节点图中，x轴表示信息传播模型中的时间步t，y轴表示节点的影响数量。

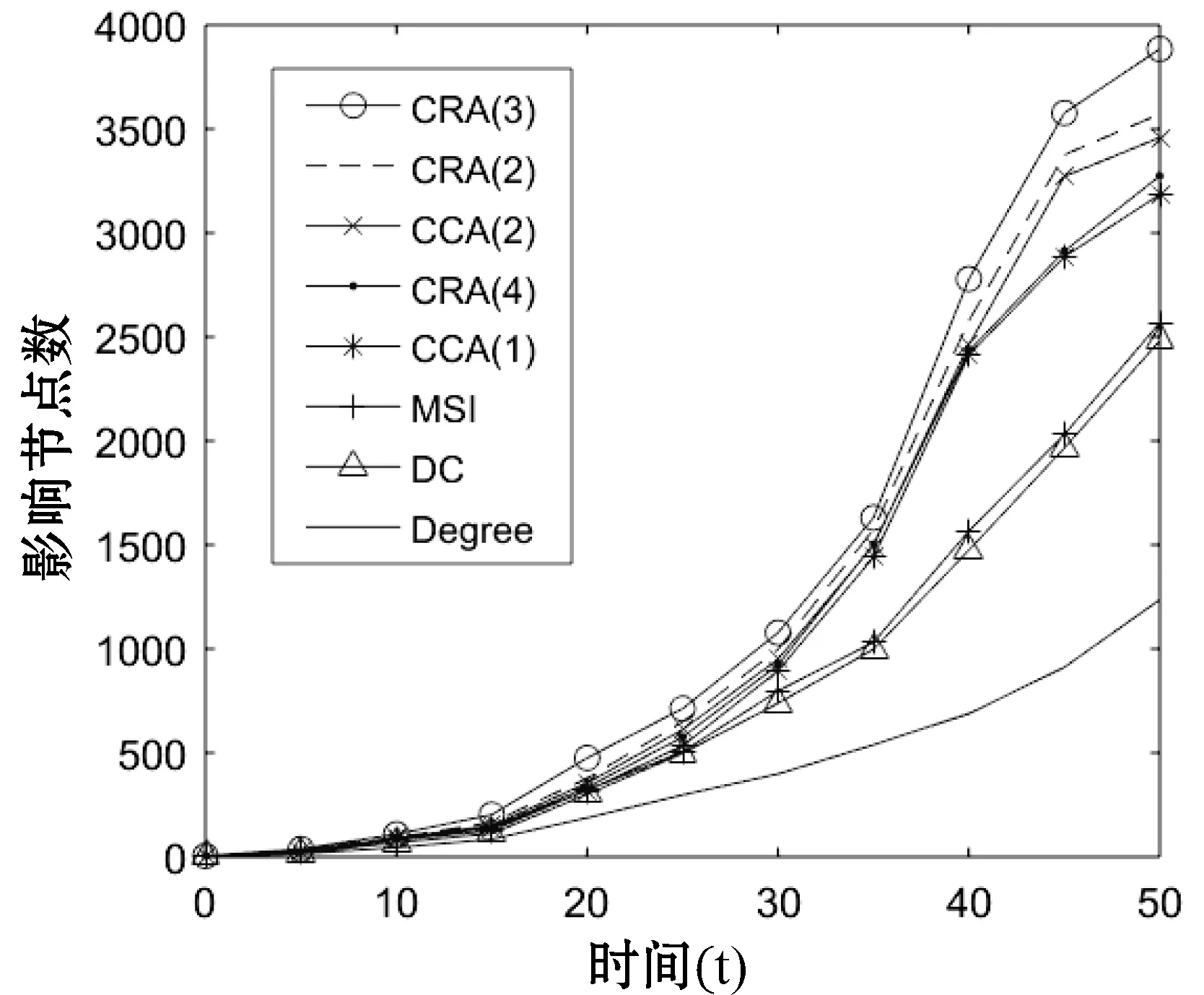
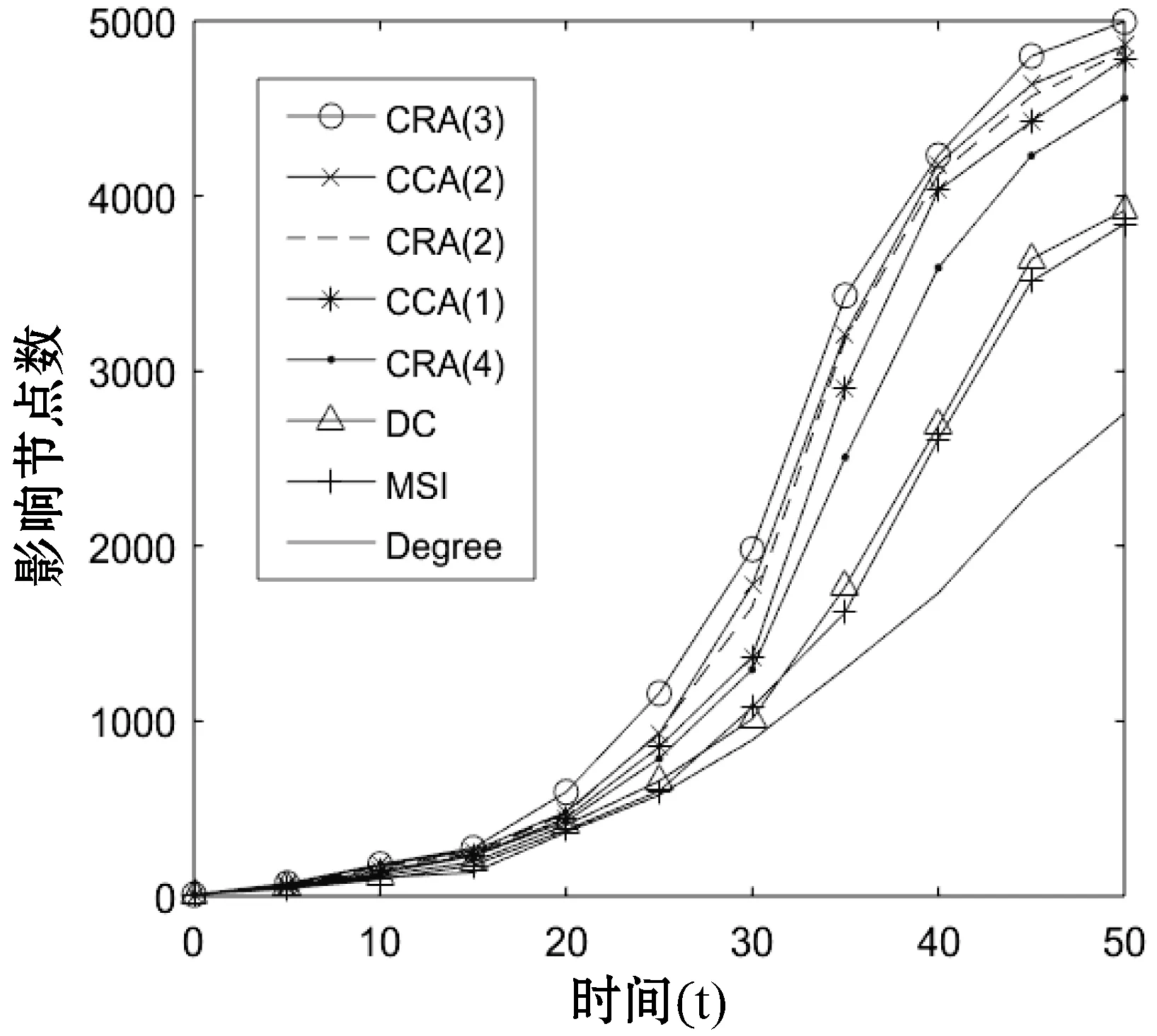
本文将初始节点m分别为5和10进行实验。在SI信息传播模型和ESI信息传播模型上，α分别为0.01、0.02和0.03。实验结果如图2、图3所示。

(a) m=5 α=0.01

(b) m=5 α=0.02

(c) m=5 α=0.03

(d) m=10 α=0.01

(e) m=10 α=0.02

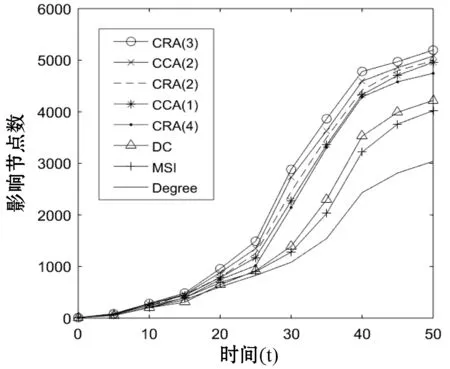
(f) m=10 α=0.03图2 SI信息传播模型上各算法的影响效果

(a) m=5 α=0.01

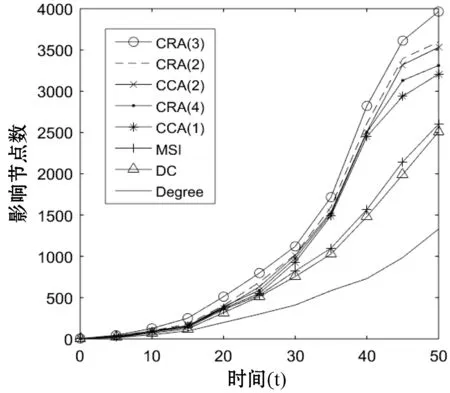
(b) m=5 α=0.02

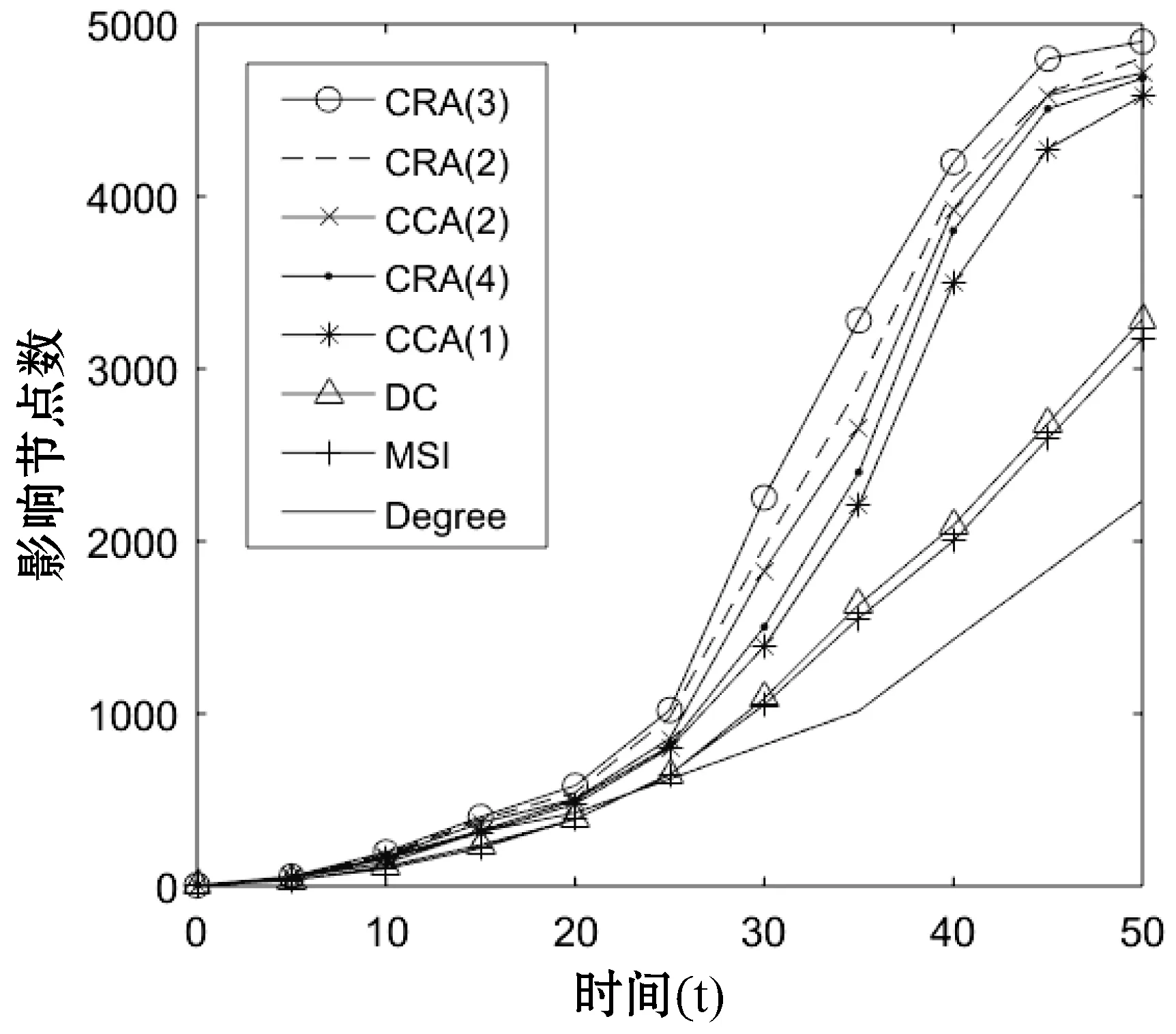
(c) m=5 α=0.03

(d) m=10 α=0.01

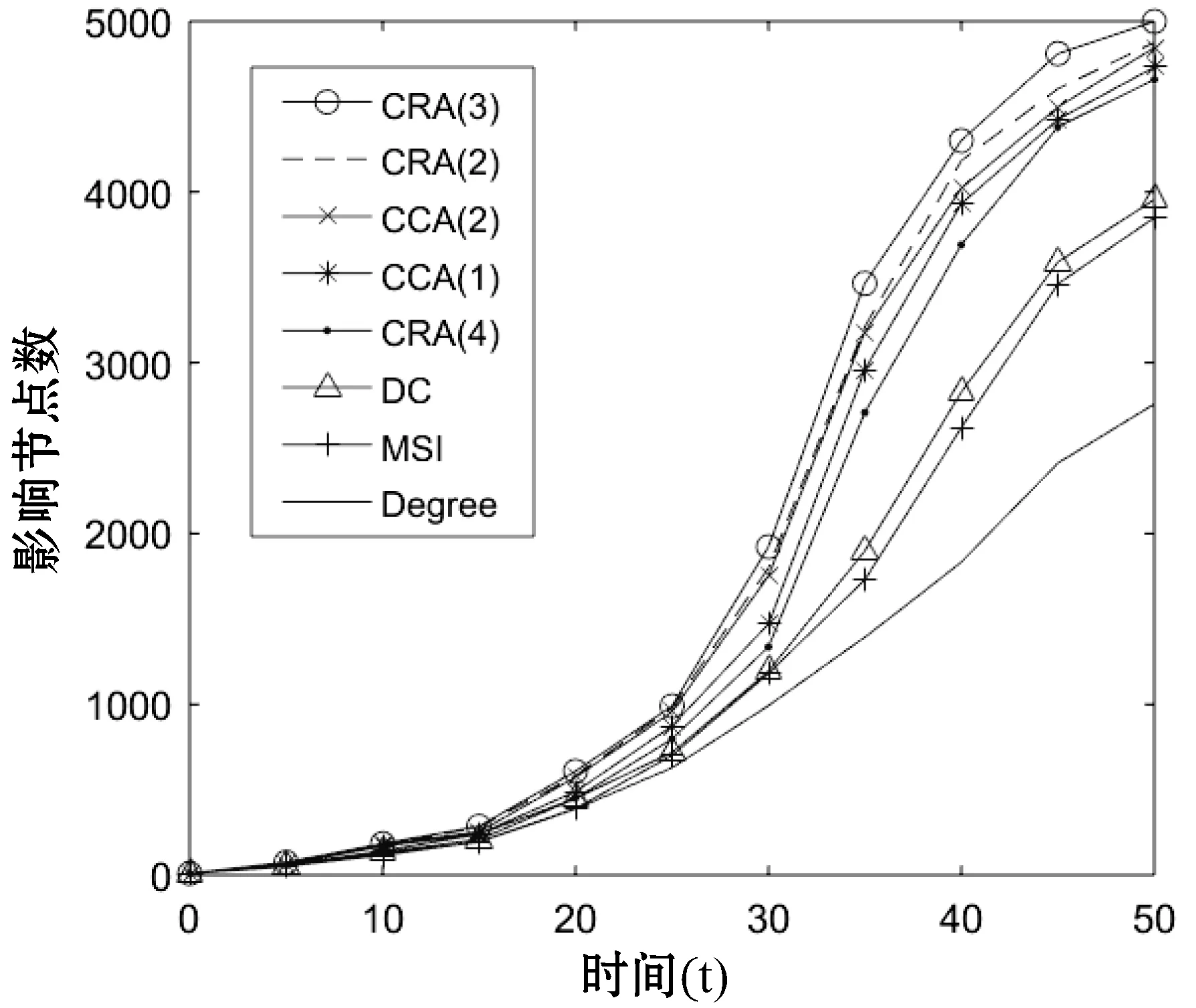
(e) m=10 α=0.02

(f) m=10 α=0.03图3 ESI信息传播模型上各算法的影响效果

从图2和图3的对比可以看出，算法在ESI信息传播模型上节点影响效果要优于SI信息传播模型，其中CRA、CCA、Degree算法比较明显，这表明节点间的亲密关系对节点的传播也起很重要的作用。而且本文提出的CRA算法比其他四种算法的最终的影响效果明显更好。在影响数量上，相同的初始节点m和影响概率α情况下，CRA的最终影响节点数量都是最多的。在影响速度上，CRA算法影响节点速度也是最快的。如图2(b-f)和图3(b-f)所示，CRA(3)比CCA(2)算法的性能更好，这充分证明考虑节点的k级节点关联特性比节点的层次性更重要。如图2(e-f)和图3(e-f)所示，DC算法的影响效果优于MSI算法，同时Degree算法影响效果变的趋于平缓。这表明节点的影响最大化过程一定要考虑初始节点的距离因素。在本文实验中，CRA(2)、CRA(3)比CRA(4)算法的影响效果更优。这主要是因为CRA(4)算法考虑的是四阶邻居节点特征，在节点的传播过程中，离初始节点远的节点不易被影响。一旦存在未影响的节点，那么这些未影响节点的邻居节点更不易影响。虽然重合率保证存在一些重复的边缘节点，使它们可以多次被影响，但是并不能保证这些重复节点一定被影响。所以并非阶数k越大，CRA算法性能越好。阶数k需要根据总节点数适宜选取。

4 结 语

本文针对社交网络节点影响最大化问题，根据节点的k阶核心集与重合率，提出了CRA算法。针对SI信息传播模型未考虑邻居节点间的亲密度的问题，对其进行改进得出ESI传播模型。分别在SI信息传播模型和ESI信息传播模型进行实验，与其他几种算法进行比较，得到如下结论：1) 所有算法在ESI信息传播模型下，节点影响效果更好。2) 在不同的传播概率下，CRA算法的影响效果都是最好的，传播过程中影响节点的速度也是最快的。在接下来的研究中，一方面是通过机器学习的方法来更加准确地预测节点间的影响概率。另一方面是推算数据集节点总数与k阶核心集特性对k值的影响，并推导使节点影响最大化的k值。

[1] Chen W, Wang Y, Yang S. Efficient influence maximization in social networks[C]// ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2009:199- 208.

[2] Zhang H, Dinh T N, Thai M T. Maximizing the Spread of Positive Influence in Online Social Networks[C]// IEEE, International Conference on Distributed Computing Systems. IEEE, 2013:317- 326.

[3] Jiang B, Hegde N, Massoulie L, et al. How to Optimally allocate your budget of attention in social networks[C]// INFOCOM,2013 Proceedings IEEE.IEEE,2013:2373- 2381.

[4] Borgs C, Brautbar M, Chayes J, et al. Maximizing social influence in nearly optimal time[C]// Acm-Siam Symposium on Discrete Algorithms.Society for Industrial and Applied Mathematics, 2014:946- 957.

[5] Wei Z, Ye Y, Tan H, et al. Information Diffusion Model Based on Social Network[C]// Proceedings of the 2012 International Conference of Modern Computer Science and Applications. Springer Berlin Heidelberg, 2013:145- 150．

[6] Xu B,Liu L.Information diffusion through online social networks[C]// IEEE International Conference on Emergency Management and Management Sciences.IEEE,2010:53- 56.

[7] Lu Z, Wen Y, Cao G. Information diffusion in mobile social networks: The speed perspective[C]// INFOCOM, 2014 Proceedings IEEE. IEEE, 2014:1932- 1940.

[8] Gopalan A, Banerjee S, Das A K, et al. Random mobility and the spread of infection[C]// INFOCOM, 2011 Proceedings IEEE. IEEE, 2011:999- 1007.

[9] Zhang H, Dinh T N, Thai M T. Maximizing the Spread of Positive Influence in Online Social Networks [C]//IEEE, International Conference on Distributed Computing Systems.IEEE,2013:317- 326.

[10] Xu B,Liu L.Information diffusion through online social networks[C]// IEEE International Conference on Emergency Management and Management Sciences.IEEE,2010:53- 56.

[11] Hacid H,Hacid H.A predictive model for the temporal dynamics of information diffusion in online social networks[C]// International Conference on World Wide Web.ACM,2012:1145- 1152.

[12] Richardson M,Domingos P. Mining knowledge-sharing sites for viral marketing[C]//Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM,2002:61- 70.

[13] Zhang Wei,Ye Yanqing,Tan Hanlin, et al. Information Diffusion Model Based on Social Network[C]// Proceedings of the 2012 International Conference of Modern Computer Science and Applications. Springer Berlin Heidelberg, 2013: 145- 150．

[14] Tang Y, Xiao X, Shi Y. Influence maximization: near-optimal time complexity meets practical efficiency[C]// SIGMOD’14 Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data.2014: 75- 86.

[15] Kimura M, Saito K. Approximate Solutions for the Influence Maximization Problem in a Social Network[C]// Knowledge-Based Intelligent Information and Engineering Systems, International Conference, Kes 2006, Bournemouth, Uk, October 9- 11, 2006, Proceedings. DBLP, 2006:937- 944.

[16] Kempe D, Kleinberg J. Maximizing the spread of influence through a social network[C]// ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM,2003:137- 146.

[17] Goyal A, Lu W, Lakshmanan L V S. CELF++: optimizing the greedy algorithm for influence maximization in social networks[C]// International Conference Companion on World Wide Web. ACM, 2011:47- 48.

[18] Chen W,Lu W,Zhang N.Time-Critical Influence Maximization in Social Networks with Time-Delayed Diffusion Process[J]. Chinese Journal of Engineering Design, 2012, 19(5):340- 344.

[19] Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex networks[J]. Nature Physics, 2011, 6(11):888- 893.

[20] Zhou T, Cao J, Liu B, et al. Location Based Influence Maximization in Social Networks[C]// ACM International on Conference on Information and Knowledge Management. ACM, 2015:1211- 1220.

[21] Estevez P A, Vera P, Saito K. Selecting the Most Influential Nodes in Social Networks[C]// International Joint Conference on Neural Networks. IEEE, 2007:2397- 2402.

[22] 曹玖新, 董丹, 徐顺,等. 一种基于k-核的社会网络影响最大化算法[J]. 计算机学报, 2015, 38(2):238- 248.

[23] Zhao J.Initial spreaders in online social networks[C]// Communication,Control,and Computing.IEEE,2017:180- 186.

[24] http://open.weibo.com/.