基于AVMD-DE和IBSA-KELM的混沌网络流量组合预测

陈 颖 魏 臻, 程 磊,(合肥工业大学计算机与信息学院 安徽 合肥 30009)(合肥工业大学安全关键工业测控技术教育部工程研究中心 安徽 合肥 30009)

0 引 言

随着网络技术的发展，网络流量已成为网络管理的关键参数之一。网络流量的分析和预测是研究网络资源分配策略、建立网络拥塞机制、提高网络服务质量和发现网络异常行为的基础。因此，建立准确度高的网络流量预测模型一直是国内外专家和学者的重要研究课题。

传统的网络流量预测方法包括自回归滑动平均模型[1]、人工神经网络[2]、支持向量机[3]等。由于网络流量是多因素影响的非线性、非平稳时间序列，具有自相似性和多重分形等特性，对流量变化特性进行先验分析能有效提高预测的精度，文献[4]提出一种基于经验模态分解EMD(Empirical Mode Decomposition)的ARMA-SVR预测模型，文献[5]提出一种基于局部均值分解LMD(Local Mean Decomposition)的GARCH预测模型，但经验模态分解和局部均值分解在数据分解过程中具有模态混叠和端点效应的问题，影响了网络流量预测精度的提高。

本文结合变分模态分解和极限学习机的优点并进行改进，提出一种基于AVMD-DE和IBSA-KELM的组合预测模型。首先对原始网络流量序列进行混沌特性分析，利用自适应变分模态分解(AVMD)方法将原始网络流量序列分解为若干子序列；其次利用分散熵(DE)分析子序列的复杂度，并根据分散熵值的不同进行合并；然后应用改进鸟群算法(IBSA)优化核极限学习机(KELM)的模型对重组后的子序列分别预测；最后将各分量的预测值进行叠加。本文通过实际网络流量数据仿真实验证明模型的有效性。

1 自适应变分模态分解

变分模态分解VMD(Variational Mode Decomposition)是K.Dragomiretskiy等[6]在2014年提出的一种新型信号特征提取方法。变分模态分解能避免传统的小波变换、经验模态分解、局部均值分解等方法中存在的模态混叠和端点效应问题，并且在信号具有噪声的情况下也能表现出良好的鲁棒性。VMD的分解过程详见文献[6]。

变分模态分解在处理信号时需要预先设定分解子序列IMF的个数K，文献[7]采用观察中心频率的方法确定分解数K，即计算不同K值下子序列的中心频率，如果出现中心频率相近的情况则认为出现过分解，则最佳分解层数取为K-1。文献[8]提出基于能量准则迭代停止条件的改进方法，当信号分解余量的能量与原始信号自身能量之比小于一定的阈值时停止。由于变分模态分解性能受分解模态总数K、惩罚因子α和Lagrange乘子更新步长τ多因素的影响，本文提出基于不同子序列最小中心频率比值的迭代停止方法，并且针对VMD的惩罚因子α和Lagrange乘子更新步长τ，提出基于分解结果均方误差MSE(Mean squared error)最小化的参数优化方法，自适应变分模态分解算法的主要步骤如下：

(1) 初始化K值，计算K=2,3，…,n时，经过变分模态分解后k个子序列的中心频率fK(k)，通过子序列功率谱的频率加权积分(或累加和)与总能量的比值求出中心频率。

(2) 计算k个子序列中相邻的两个中心频率的比值，如式(1)所示，记为γK,1,γK,2,…,γK,k-1，取这k-1个比值中的最小值记为γK,min，如式(2)所示。

(1)

γK,min=min{γK,1,γK,2,…,γK,k-1}

(2)

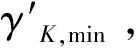
(3)

(4) 预置惩罚因子α值范围为[20,2 000]，步长为20；预置Lagrange乘子更新步长τ值范围为[0.01,1]，步长为0.01，代入最佳分解层数K迭代计算不同α和τ值下分解重组的均方误差值，选取均方误差最小值的α和τ作为最优参数。

(5) 代入最优分解层数K、参数α和τ，输出最优分解结果。

2 分散熵

分散熵DE是M. Rostaghi等[9]在2016年提出的一种新型量化时间序列复杂度的方法，具有比样本熵更快的计算速度，并且避免了排列熵忽视信号幅度和振幅值的问题，对于给定时间序列x={x1,x2,…,xn}，计算分散熵步骤如下：

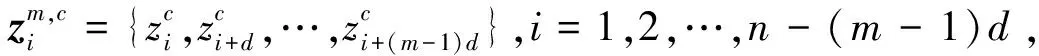
(3) 对cm个的分散模式计算其相对频率：

p(πv0v1…vm-1)=

(4)

(4) 计算分散熵：

(5)

3 基于IBSA-KELM的预测模型

3.1 改进鸟群算法

鸟群算法BSA(Bird Swarm Algorithm)是由Xian-Bing Meng等[10]在2016年提出的一种新型元启发式群智能优化算法。该算法主要包括自然界中鸟群觅食、警惕和飞行三个行为，鸟群基于三种行为并通过信息共享机制及搜索策略最终搜索到最优解。改进鸟群算法的寻优过程如下：

(1) 觅食行为。利用Logistics映射作为混沌映射初始化i只鸟在D维空间的初始位置，每只鸟根据个体经验和群体经验觅食。本文在位置更新过程中加入随机惯性权重避免陷入局部最优，同时对式(6)中的认知因子C和群体加速因子S采用余弦函数进行动态调整，表达式如下：

(6)

ω=ωmin+(ωmax-ωmin)·rand(0,1)+σ·randn(0,1)

(7)

(8)

(9)

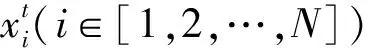
(2) 警戒行为。每只鸟都会试图向群体中心移动。警觉性高的比警觉性低的鸟更容易接近于群体中心，它们将相互竞争，表达式如下：

(10)

式中：A1表示环境影响因子，A2表示特定干扰影响因子，meanj表示群体第j维的平均位置。

(3) 飞行行为。警觉性高的鸟作为生产者寻找食物，警觉性低的鸟成为索取者从生产者获取食物。生产者和索取者可以脱离群体，表达式如下：

(11)

(12)

式中：FL(FL∈[0,2])表示索取者会追随生产者寻找食物的因子。

3.2 核极限学习机

核极端学习机KELM是由Guang-Bin Huang等[11]提出的，相比于极限学习机(ELM)，KELM算法不仅加快了传统神经网络的收敛速度、避免陷入局部最优并具有良好的泛化性能，而且通过核函数映射确定ELM隐含层的结构[12]。ELM算法是单隐层前馈神经网络(SLFNs)的机器学习算法，其训练方法可以最小化输出权值和训练误差，如式(10)所示：

(13)

式中：β是隐含层输出权值向量，h(xi)为隐含层输出向量，ξi为训练输出误差，yi为理论输出，C为惩罚参数。根据KKT最优化条件解得：

(14)

式中：H为隐含层的输出矩阵，T为目标值的矩阵。根据Mercer’s条件定义核矩阵形式如下：

ΩELM=HHT

ΩELM i,j=h(xi)·h(xj)=K(xi,xj)

(15)

式中：i,j=1,2,…,N，K(xi,xj)为核函数。则KELM模型的输出函数可以表示为：

(16)

本文KELM采用Guass径向基核函数：

K(xi,xj)=exp(-γ‖xi-xj‖2)

(17)

式中：γ为核函数参数。本文采用IBSA算法对KELM的正则化系数C和核函数参数γ进行优化，提升KELM算法的预测精度。

4 实验分析

仿真实验采用的网络流量数据来自英国学术主干网，选择2004年11月22日到2005年1月24日的1 500条采样间隔为1小时的数据，选取前1 212个数据组成训练集，选取后288个数据组成测试集。图1为实际的英国学术主干网络流量数据。

图1 网络流量时间序列

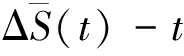
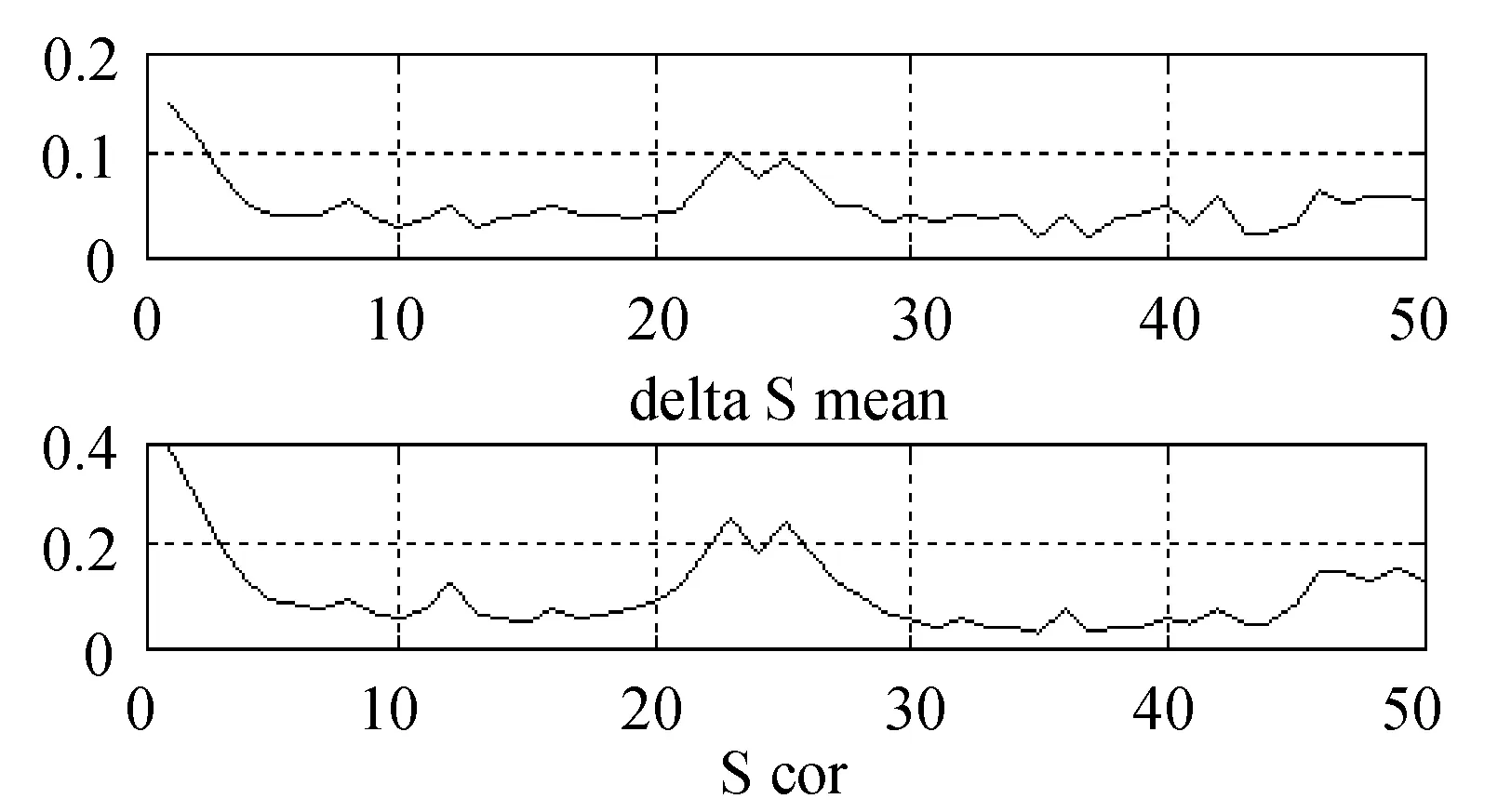
图和Scor(t)-t

对原始网络流量数据进行归一化处理，计算K=2,3，…,n时，经过变分模态分解后k个子序列的中心频率fK(k)，计算相邻两个中心频率的比值记为γK,1,γK,2,…,γK,k-1，取k-1个比值中的最小值γK,min，如表1所示。

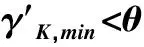
表1 不同K值时

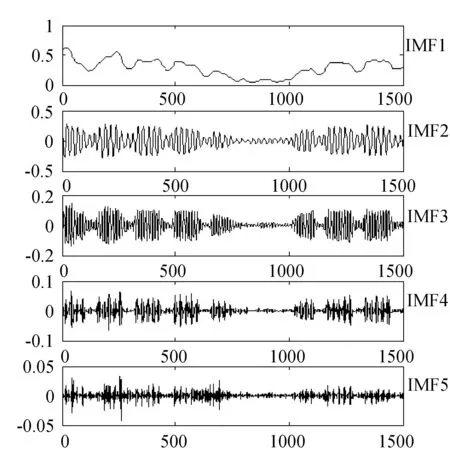
图3 自适应变分模态分解(AVMD)的子序列

由图3可见，经过自适应变分模态分解后的子序列具有较强的规律性，同时分解后产生的IMF 子序列较多。为了降低网络流量预测的计算规模，采用分散熵算法对每一个 IMF子序列进行复杂度分析。分散熵的计算过程中，需要考虑参数的影响，本文参数选择m=9，c=6，t=5，计算各IMF分量的分散熵值如图4所示。

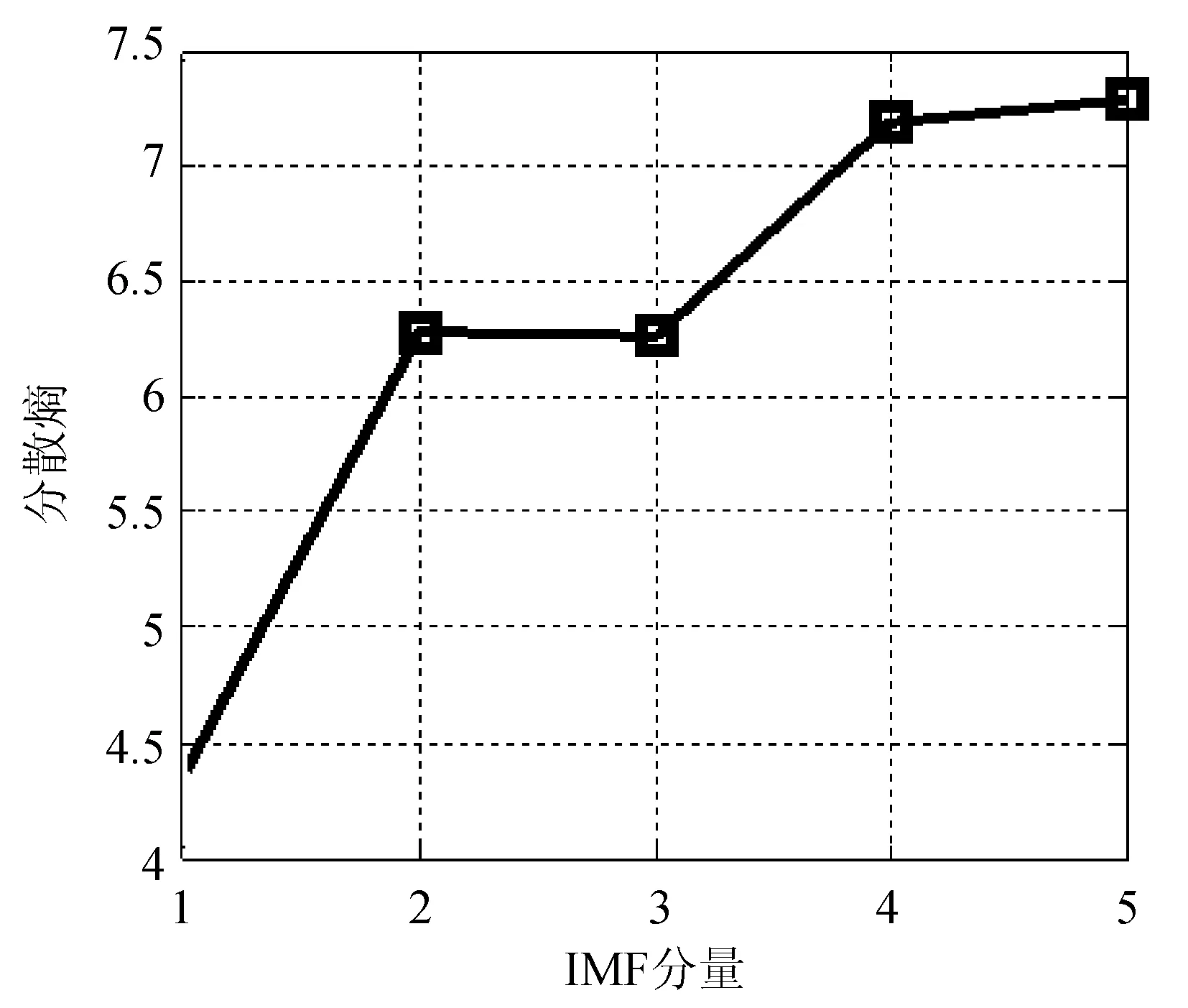
图4 IMF子序列的分散熵

经过变分模态分解后的IMF子序列的分散熵值具有递增的趋势，表明从子序列的复杂度随中心频率增大。将分散熵值相近的IMF 子序列进行合并，降低预测的计算规模。同时对重组后的子序列采用C-C算法进行相空间重构，计算重构后子序列的嵌入维数m和时间延迟t。子序列重构结果及相空间重构参数如表2所示。

表2 IMF子序列合并

组合预测模型的预测值和实测值的对比结果如图5所示。本文采用平均绝对百分比误差(MAPE)、希尔不等系数(TIC)和相关系数(R)作为模型预测精度的性能评价指标。

图5 AVMD-DE-IBSA-KELM预测效果

(18)

(19)

(20)

表3 5种模型预测结果对比

5 结 语

本文结合变分模态分解、分散熵、鸟群算法和极限学习机的优点，应用自适应变分模态分解和分散熵的组合模型处理网络流量序列，并提出基于改进鸟群算法优化核极限学习机的组合预测模型。通过英国学术主干网的实测网络流量数据进行验证，并与KELM模型和EMD-KELM等预测模型对比。仿真结果表明，AVMD-DE和IBSA-KELM组合模型对网络流量的预测误差更小、效果明显更优，具有很好的应用价值。

[1] Laner M, Svoboda P, Rupp M. Parsimonious fitting of long-range dependent network traffic using ARMA models[J]. IEEE Communications Letters, 2013, 17(12):2368- 2371.

[2] 王雪松,梁昔明. 基于BPSO-RBF神经网络的网络流量预测[J]. 计算机应用与软件,2014,31(9):102- 105.

[3] 路璐,程良伦. 改进布谷鸟搜索算法优化SVM的网络流量预测模型[J]. 计算机应用与软件,2015,32(1):124- 127.

[4] Dai L, Yang W, Gao S, et al. EMD-based multi-model prediction for network traffic in software-defined networks[C]//Mobile Ad Hoc and Sensor Systems (MASS), 2014 IEEE 11th International Conference on. IEEE, 2014: 539- 544.

[5] Yimu J, Yongge Y, Chuanxin Z, et al. Research of a Novel Flash P2P Network Traffic Prediction Algorithm[J]. Procedia Computer Science, 2015, 55: 1293- 1301.

[6] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE transactions on signal processing, 2014, 62(3): 531- 544.

[7] 刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊 C 均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13): 3358- 3365.

[8] 唐贵基, 王晓龙. IVMD融合奇异值差分谱的滚动轴承早期故障诊断[J]. 振动、测试与诊断, 2016, 36(4):700- 707.

[9] Rostaghi M, Azami H. Dispersion entropy: A measure for time-series analysis[J]. IEEE Signal Processing Letters, 2016, 23(5):610- 614.

[10] Meng X B, Gao X Z, Lu L, et al. A new bio-inspired optimisation algorithm: bird swarm algorithm[J]. Journal of Experimental & Theoretical Artificial Intelligence, 2016, 28(4):673- 687.

[11] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006,70(1):489- 501.

[12] 王新迎, 韩敏. 多元混沌时间序列的多核极端学习机建模预测[J]. 物理学报, 2015,64(7):070504.

[13] Kim H S, Eykholt R, Salas J D. Nonlinear dynamics, delay times, and embedding windows[J].Physica D: Nonlinear Phenomena, 1999, 127(1):48- 60.

[14] Rasheed B Q K, Qian B. Hurst exponent and financial market predictability[C]//IASTED conference on Financial Engineering and Applications (FEA 2004). 2004:203- 209.