电力系统可靠性评估综述

华南理工大学电力学院 黄 超 尹华杰

0 引言

随着电力系统的高速发展，电力系统日趋复杂化、高效化和智能化。如何快速准确地评估电力系统可靠性水平对电力系统的日常规划和实际运行都具有重要意义[1-2]。

电力系统可靠性评估是指对电力系统遭遇随机事件时的停电风险进行量化评估和分析，通过各种测量指标从不同方面对电力系统抵御各种不利随机事件的能力进行量化描述，从而揭示电力系统的薄弱环节和安全裕度水平。电力系统的可靠性水平依赖于电力系统元件的随机故障，传统的电力系统可靠性评估的方法主要有两大类：解析法[3]和MC方法[4]。解析法和MC方法各有优点和不足之处以及适用范围。经历了半个多世纪的发展，电力系统可靠性研究在理论和实践方面取得了非常可观的成果。文献[5]深入研究了MC方法的收敛特性和样本容量的概率不确定，提出将核密度估计技术用于可靠性评估中，对可靠性指标的概率密度进行估计，探索了从可靠性指标内在分布规律和结构特征出发深刻揭示电网风险特性的新思路；文献[6]提出了将混合方法用于电力系统可靠性评估中，MC方法和解析法的优点得到充分利用，通过简单判断系统每次采样的状态，该方法有效的减少了每一次状态评估所需要的时间，使得计算效率得到了成倍提高，但系统的薄弱环节得不到有效识别；文献[7]将QMC用于电力系统可靠性评估中，证明了将QMC方法用于可靠性评估的可行性，但由于算例的系统规模较小，QMC相对于MC的改进效果比较明显；文献[8]将QMC与MC在电力系统可靠性评估中的应用进行了对比，但是结论显示QMC的改进不明显，QMC方法最主要的优点是用低偏差点列(low discrepancy sequence,LDS)，但是LDS的均匀性会随着序列维数的增加而不断退化，文献中由于系统的规模比较大，LDS的均匀性退化比较严重，QMC方法的效果不是很明显；因此，将QMC方法直接应用于电力系统可靠性评估中存在一定的局限性。文献[9]中建立了基于维度重要性的可靠性评估的QMC模型和交叉熵QMC模型，并提出计算值与真实值之间的误差的精度指标。

1 解析法的基本原理

解析法主要通过建立数学模型来对电力系统可靠性进行评估，它的主要优点是其物理概念清楚，模型精度高。通过解析法计算得到的可靠性指标是系统的平均值指标，但是解析法不适用于规模较大的系统。因为当系统的规模较大时，计算的工作量会随着元件个数的增加而成指数增长。故当系统规模小、元件数目不多时使用解析法可以充分发挥它物理概念清楚、模型精度高的优点。解析法按照其分析方法的原理不同主要可分为故障模式后果分析法[8]、状态空间法[9]、网络等值法[10]等。

解析法首先对事故状态进行枚举，然后对系统的故障进行选择，再综合分析所枚举的故障状态、评估系统的可靠性水平。即先选择一种停运状态进行枚举，然后再用已经确定的可靠性准则对该停运状态进行潮流分析。对全部故障状态进行枚举，系统的可靠性指标就能计算出来。

解析法可靠性计算标准公式如下：

式中：xi是第i个系统的状态；P(xi)—当前系统处于状态xi的概率；If(xi)—状态xi的二值函数(系统在正常工作状态下取0，故障状态下则取1)；—随机函数F(xi)的精确期望值的估计；

由于系统内多个元件同时发生故障的概率很小，对可靠性指标的影响也非常小，因此，可以忽略不计。故在用解析法进行可靠性评估时通常不考虑多个元件同时发生故障时对系统的影响。

2 蒙特卡洛法的基本原理

MC方法由于其灵活性和实用性，在电力系统可靠性评估中占据了重要位置。MC方法一般用方差系数作为收敛判据，一般认为当它的方差系数减少到某一程度时，可靠性指标就得到了收敛。为此有些学者提出了一些减少方差的技术用来提高MC方法的计算效率，如控制变量法，分层抽样法，重要抽样法。MC方法根据其抽样原理的不同可分为非序贯蒙特卡洛方法(non-sequential Monte Carlo method)和序贯蒙特卡洛法(sequential Monte Carlo)，由于其原理各不相同，两者各有优点和不足之处。

2.1 非序贯蒙特卡洛法的基本原理

非序贯蒙特卡洛一般采用状态抽样。假设系统有m个元件，且系统中每个元件的状态只有两种形式，即故障模式和运行模式，则系统中第i个元件的状态为Si，则系统的状态x是系统中每个元件的状态集合，所以只要确定了系统中每个元件的状态，就能确定系统的状态x。设第i个元件的强迫停运率为Qi，则系统中每个元件的概率特性都可以用一个处在[0,1]之间的均匀分布来描述，随机抽取一个处在[0,1]之间均匀分布的数Qi，则第i个元件的状态为：

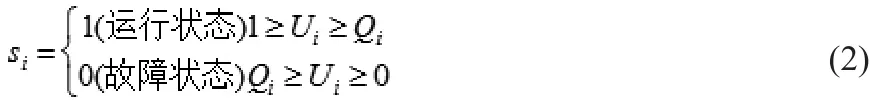
首先随机抽取n个随机数U1,U2,…,UN；由公式(2)便可以得到系统中每一个元件的运行状态x，然后重复上述步骤M次，就可以得到一个包含M个系统状态样本的集合x={X1,…,Xk，…,XM}。

可靠性指标的标准近似估计值的公式如下：

式中：N—系统总的抽样次数；F(xi)—系统自变量状态xi的样本函数；E—函数F(xi)的样本均值，当样本函数F(xi)取不同的函数时，便可得到不同的可靠性指标。

利用非序贯蒙特卡洛法进行可靠性评估的主要优点在于其抽样方法简单，算法易于实现。它的主要缺点是在进行可靠性评估时，故障持续时间和故障频率等相关可靠性指标的计算难度太大。利用非序贯蒙特卡洛模拟法计算电力系统可靠性指标时，抽样点数的数值如果太大的话将会导致可靠性计算成本太高，因此在实际运用中，应该根据工程所能允许的实际误差范围，适当的选择抽样点数的数值，以达到计算精度和计算效率的最优化。

2.2 序贯蒙特卡洛方法的基本原理

序贯蒙特卡洛方法需要对系统中各个元件的状态进行抽样，可靠性指标标准计算公式如下：

式中：xt—t时刻系统的状态；f(xt)—自变量xt的性能测试函数；T—模拟总时间；—可靠性指标期望值的近似估计值；当模拟时间T足够长时，系统指标也将收敛于一个稳定的期望值E。

状态持续时间抽样是按照时序，在一个时间间隔上对系统的运行过程进行模拟，由于系统运行时一般是在某一状态停留一段时间然后由于随机事件的发生而转移到另外一种状态，因此，它的变化并不是连续得，所以系统在实际运行过程是离散化不连续的，在模拟总时间为n年的过程中系统第i年的状态序列为{xi1,xi2,…,xij}，则可进一步离散化为：

式中：xij—系统第i年j时刻的状态；f(xij)—可靠性指标测试函数；D(xij)—系统第i年处于状态xij持续的时间；Fi—系统第i年的可靠性指标；

序贯蒙特卡洛方法由于按照时间推移对系统的随机特征进行模拟，所以在计算系统的频率与持续时间有关的可靠性指标方面具有明显的优势；其缺点是计算时间过长。

2.3 拟蒙特卡洛法的基本原理

QMC方法与MC方法相似，但QMC方法在抽样过程中用LDS代替了MC方法抽样中的伪随机序列，与MC方法中的伪随机序列相比，QMC中的LDS更加趋向于均匀性，使得QMC在可靠性评估中具有更高的积分误差求解精度。

序列的均匀性一般用星偏差进行度量。设S维单位超立方体[0,1]S中有序列{X1,X2,…,XN}，则该序列的星偏差为：

式中：μ(V)—区域V在S维单位超立方体[0,1]S中的勒贝格测度；M(X1,X2,…,XN)—点{X1,X2,…,XN}包含在区域V中的点数；

由上式可以看出，D*N的值得大小由序列中的点分布的均匀性来决定；当序列中的点分布越均匀， D*N的值越小；当序列中的点分布越分散，D*N的值越大。

QMC的积分误差阶由Koksma-Hlawka不等式给出：

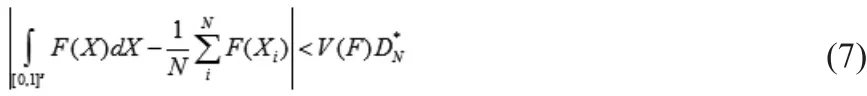
式中：V(F)—函数F在S维单位超立方体[0,1]S存在Koksma-Hlawka不等式意义下的有界变差；D*N—点列{X1,X2,…,XN}的星偏差；

公式(6)中，V(F)有界变差为定值，积分误差完全由随机抽样序列中的星偏差来决定，所以，只要随机抽样序列的均匀性越高，积分误差将越小。

QMC方法的核心基础是LDS的构造，Sobol点列由于其所构造的方法比较简单，点列均匀性比较好而成为最近应用最广泛的一种点列。文献[6]给出了构造一维情况下Sobol点列的方法，文献[11]给出了构造多维情况的下Sobol点列的方法；由于LDS为固定性序列，在模拟中当抽样点数固定时，运用QMC进行可靠性评估计算出的积分值为固定的值，为了将MC方法的独立性和QMC方法的超均匀性充分利用起来，有一些学者提出利用加扰技术使QMC方法随机化，使得在抽样过程中保证为LDS的同时又使LDS具有一定的随机性。

3 展望

本文指出了电力系统可靠性评估的目的和意义，详细的介绍了当前电力系统可靠性评估常用的两类方法，并对这两类方法进行对比分析，指出了这两类方法的优点和不足之处。目前常用的可靠性评估方法仍有许多地方有待改进，QMC方法作为电力系统可靠性评估中的一种新方法、新思维，可进一步研究确定性的LDS，为后续电力系统的可靠性评估的研究提供一定的参考。

[1]张焰.电网规划中的模糊可靠性评估方法[J].中国电机工程学报,2000, 20(11):77-80.

[2]王天华,王平洋,范明天.用0-1规划求解馈线自动化规划问题[J].中国电机工程学报,2000,20(5):54-58.

[3]卢锦玲,杨晓东,栗然,等.一种基于贝叶斯网络的配电网可靠性评估方法[J].华北电力大学学报(自然科学版), 2004, 31(2):16-19.

[4]Reliability Evaluation of Power System[J].Science & Technology Vision,2017.

[5]赵渊,徐焜耀,吴彬.大电力系统可靠性评估的蒙特卡洛仿真及概率密度估计[J].重庆大学学报,2007,30(12):16-20.

[6]别朝红,王秀丽,王锡凡.电力系统可靠性评估的混合法研究[C].中国电机工程学会电力可靠性学术年会,2001.

[7]侯雨伸,王秀丽,刘杰,等.基于拟蒙特卡罗方法的电力系统可靠性评估[J].电网技术,2015,39(3):744-750.

[8]侯雨伸,王秀丽,张玥,等.考虑维度重要性的电力系统可靠性评估拟蒙特卡洛方法[J].电力系统自动化,2016,40(16):31-37.

[9]张启亮,刘倩影.基于故障模式后果分析法的配网网架结构可靠性研究[J].黑龙江电力,2017,39(3):220-223.

[10]胡晓斌.基于解析法的配电系统可靠性评估[D].南昌大学,2008.

[11]别朝红,王锡凡.复杂电力系统一类连锁反应事故可靠性评估模型和算法[J].电力系统自动化,2001,25(20):30-34.

[12]Sobol I M.On the distribution of points in a cube and the approximate evaluation of integrals[J].Ussr Computational Mathematics &Mathematical Physics,1967,7(4):86-112.