基于ABAQUS的环面渐开线齿轮副传递误差分析
2018-07-04伍红平刘雷
伍红平,刘雷
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
环面渐开线齿轮是一种对安装误差不敏感,具有良好的啮合特性、较高的承载能力,并且加工便捷的新型齿轮[1-2]。该齿轮传动是一种凸—凹廓啮合传动形式,环面渐开线齿轮的齿顶曲面和齿根曲面分别为外环面或内环面的一部分,而环面由圆弧绕齿轮轴线旋转形成。凸环面渐开线齿轮的分度圆齿厚由齿宽中部向两端逐渐减小,而齿顶厚由齿宽中部向两端逐渐增大;凹环面渐开线齿轮的分度圆齿厚由齿宽中部向两端逐渐增大,而齿顶厚由齿宽中部向两端逐渐减小。
本文以环面渐开线齿轮为研究对象(图1、图2),基于有限元软件重点研究了齿轮的传递误差。对模型进行了精确的有限元前处理以确保有限元分析的有效和准确性;根据非线性静力分析得到了环面渐开线齿轮副的静态传递误差,以及转矩对齿轮静态传递误差的影响;根据非线性隐式动力学分析,得到了环面渐开线齿轮的动态传递误差。环面渐开线齿轮传递误差的分析对进一步对其修形研究以及齿轮动力学研究有重要意义。

图1 凸环面渐开线齿轮示意图
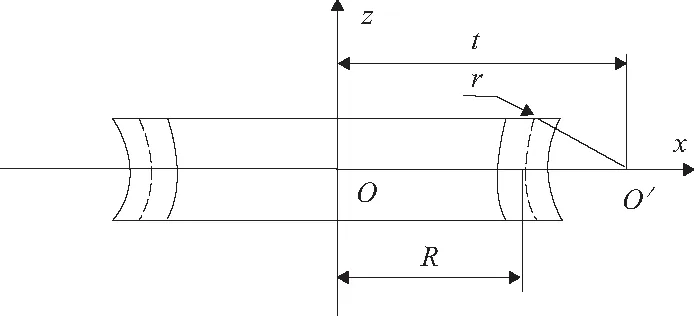
图2 凹环面渐开线齿轮示意图
1 齿轮传递误差的概念
齿轮传递误差主要由齿轮加工误差、齿轮修形量、齿轮受载变形、齿轮轴弯曲变形引起的偏载等构成。在本文所建立的有限元模型中只考虑齿轮受载变形对其传递误差影响,其中包括弯曲变形和接触变形。齿轮传递误差的计算公式如下:
TE(um)=rp1θ1-rp2θ2
(1)
式中,rp1、rp2分别为主动轮和从动轮的节圆半径;θ1、θ2为两齿轮转过的角度。
齿轮动态传递误差是齿轮系统噪声的主要来源[3],一般情况下,齿轮动态传递误差较难准确的分析和测量。但是动态传递误差是由静态传递误差引起的,通过减小静态传递误差能有效地减小动态传递误差,从而减小齿轮传动系统噪声。
国内外学者对齿轮传递误差有着大量的研究。传递误差的分析有动力学方程求解和有限元分析、实验测量等方法。Raul[4]在ABAQUS中建立了直齿圆柱齿轮的有限元模型,分析了转矩、转速、传动比等因素对齿轮静态传递误差和动态传递误差的影响,并对齿轮作了修形研究。唐进元[5]提出了一种传递误差的概念模型和力学模型,推导出了传递误差的计算公式,并给出了传递误差的一个计算实例。白玉田[6]利用有限元的方法计算出轮齿不同位置的啮合刚度,并通过切片模型计算出齿轮啮合过程中的传递误差。张义民[7]通过有限元法分析了某斜齿轮副的静态传递误差及动态传递误差,并分析了它们的主要频率成分。汪中厚[8]等对螺旋锥齿轮的传递误差有相关研究。张涛[9]等分析了制造误差对齿轮动态性能的影响并指导齿轮的减振设计和精度设计。
2 环面渐开线齿轮有限元建模
环面渐开线齿轮几何设计参数如表1所示。

表1 环面齿轮基本参数表
通过环面齿轮的齿轮生成原理,建立凸、凹环面齿轮的齿面方程,在Matlab中生成齿面各点的坐标值并导入Pro/E,建立完整的齿轮模型完成装配并进行必要的干涉检查之后,将模型导出为.x_b格式并导入到ABAQUS中。在ABAQUS中进行有限元前处理如下:
1) 网格划分:因齿轮传递误差受惯性影响,故建立两个齿轮的完整模型。考虑到计算精度及计算时间,对准备参与啮合的几对轮齿做精细划分,而其他不参与啮合的轮齿网格较粗。网格划分如图3所示,单元类型为C3D8R。

图3 环面渐开线齿轮网格划分
2) 材料参数:齿轮材料选用45钢,密度为7.8×10-9t/mm3。弹性模量和泊松比分别为210 000MPa、0.3。材料阻尼采用Ray-leigh阻尼,其中质量矩阵系数α=0.03、刚度矩阵系数β=3×10-6。
3) 耦合关系:分别在凸环面齿轮和凹环面齿轮的轴线上定义刚体参考点(reference point),参考点分别与两齿轮内圈建立耦合关系(coupling)并约束所有自由度。后续通过参考点对齿轮施加固定边界条件及位移边界条件。
4) 接触对:选择凸环面齿轮齿面为主面,凹环面齿轮齿面为从面。齿面间接触的相互作用分为法向和切向作用,其中法向作用定义为“hard contact”,切向作用的摩擦系数设置为0.1。齿面接触处采用有限滑移(finite sliding)的追踪方式计算接触表面之间的相对滑移。
3 环面渐开线齿轮副静态传递误差分析
对环面渐开线齿轮进行非线性静力学分析,从而分析其静态传递误差。
3.1 有限元设置
针对不同的分析任务,ABAQUS设置不尽相同,文中以凸环面齿轮作为主动轮,凹环面齿轮作为从动轮进行约3个啮合周期的静态分析,设置如下:
1) 分析步设置:环面渐开线齿轮静力学分析包括1个初始分析步和2个后续分析步。设置环面齿轮静力学分析的后续分析步为Static,General类型。其中第1个后续分析步的作用是建立齿面接触,其目的是使分析容易收敛,分析时间为1 s;第2个分析步为旋转分析步,分析时间为0.2 s。由于齿面接触问题为非线性问题,故2个分析步均设置为非线性分析。同时,需创建历史输出(history output requests)得到两齿轮的轴向角位移(UR3),追踪目标为上文的刚体参考点创建的节点集(Set)。为了控制角位移采样的偏差,将初始时间增量和最大时间增量均设置为0.002 s,以确保至少有100个增量步。
2) 载荷及位移边界条件设置:在初始分析步中约束主动轮的所有自由度,约束从动轮除轴向旋转外的5个自由度;在接触建立分析步中,对从动轮采用光滑(smoothing)加载的方式施加80 N·m的转矩以建立接触;在旋转分析步中,解除主动轮的轴向旋转自由度并添加1个角位移以驱动其旋转,角位移的大小为0.5 rad。
3.2 静态传递误差分析结果
读取历史输出中两齿轮的角位移θ1、θ2,在Matlab中进行一定运算处理后得到环面渐开线齿轮副在80N·m载荷下的静态传递误差如图4所示。其静态传递误差为17.5μm,静态相对传递误差(峰-峰值差)为6.9μm。结合有限元后处理中的应力应变云图知,在0~45ms(主动轮转过角度<0.11rad)时,齿轮副处于双齿啮合区,此时静态传递误差较小,这是由于双齿啮合区啮合刚度较大;在45ms时(主动轮约转过0.11rad)凸齿轮的一个轮齿啮出,齿轮副进入单齿啮合区,啮合刚度显著减小,此时传递误差增大;在67ms时(主动轮约转过0.14rad)凹齿轮的一个轮齿啮入,齿轮副重新进入双齿啮合区,啮合刚度增大,传递误差减小。

图4 环面渐开线齿轮静态传递误差
3.3 数据可靠性验算
由于所分析环面渐开线齿轮副为点接触,环面渐开线齿轮齿面较为复杂。为了验证有限元分析结果的可靠性,对环面渐开线单齿啮合区的一个接触对利用赫兹接触理论进行理论计算如下:
(2)
式中:p0为最大接触应力;
Q为接触点处的法向接触力;
a为接触椭圆的长半轴;
b为接触椭圆的短半轴;
法向接触力Q由转矩以及接触点的位置向量以及齿轮的单位法向而确定,a、b由接触点的曲率半径、主曲率方向、弹性模量以及Q等参数计算得到。
为了避免齿间载荷分配问题,选取单齿啮合区的一个接触点进行理论计算。通过环面渐开线齿轮的齿面方程、弹性模量等参数计算得到此接触点在80N·m载荷下的理论最大接触应力为629MPa,对比图5中的有限元分析结果643MPa,理论结果与有限元结果基本一致,故认为有限元在环面渐开线齿轮静力学分析中可靠,通过有限元静力学分析取得静态传递误差的方法是可行的。

图5 转矩对静态传递误差的影响
3.4 转矩对静态传递误差的影响分析
为了分析不同转矩对环面渐开线齿轮副静态传递误差的影响,采用相同的步骤在其他不同的转矩下(20N·m、40N·m、60N·m、100N·m)进行静力学分析,得到不同转矩下该参数环面渐开线齿轮副的传递误差如图6所示。结果表明在一定范围内随着转矩的增大静态传递误差也增大,传递误差峰值位置及其变化趋势相当一致。为了进一步了解静态传递误差与转矩的关系,在Matlab中对其进行线性拟合,结果如图7。分析结果表明在一定范围内,该参数环面渐开线齿轮的静态传递误差随着转矩的增大线性增大,同时其相对传递误差也随着转矩的增大而增大。

图6 不同转矩下的静态传递误差

图7 转矩对静态传递误差的影响
4 环面渐开线齿轮副动态传递误差分析
对环面渐开线齿轮进行非线性隐式动力学分析,从而分析其动态传递误差。
4.1 有限元设置
1) 分析步设置:环面渐开线齿轮动力学分析只包括一个初始分析步和一个后续分析步。设置环面齿轮静力学分析的后续分析步为Dynamic,Implicit类型,并打开非线性。同样动力学分析也需创建历史输出(history output requests)得到两齿轮的轴向角位移(UR3)进行追踪。根据下文设置的主动轮转动速度(20 rad/s),为保证有3个啮合周期的仿真,将分析时间设置为0.025 s,将初始时间增量和最大时间增量均设置为0.000 1 s。
2) 定义接触对:由于环面渐开线齿轮齿面的复杂性以及接触问题易产生收敛问题,在隐式动力学分析中将齿面间接触属性的法向作用由硬接触(hard contact)更改为指数式(exponential)“软”接触,设置p=1 000,c=0.001;切向作用的摩擦系数仍设置为0.1。指数形式接触[10]是指法向接触间隙减小到c时,接触面进入接触约束;接触间隙减小到0时,接触压力为p;在接触间隙为c到穿透距离为6c之间,接触压力与接触间隙满足指数关系;当穿透距离大于6c时,接触压力与接触间隙为线性关系。
3) 载荷及位移边界条件设置:为了动力学分析尽快进入到平稳状态,在ABAQUS中创建预定义场(predefined Field),设置主动轮的转速为20 rad/s,从动轮的转速由齿轮副的传动比计算得到,为-17.96 rad/s。在初始分析步中约束主动轮和从动轮除轴向旋转外的5个自由度;在隐式动力学分析步中,对主动轮施加一个角速度驱动,角速度大小为20 rad/s,对从动轮施加80 N·m的转矩。
4.2 动态传递误差分析结果
读取输出中两齿轮的角位移θ1、θ2,在Matlab中进行一定运算处理后得到环面渐开线齿轮副在80N·m载荷、20rad/s的转速下的动态传递误差并与静态传递误差对比如图8。结果表明,在初始啮合阶段,由于啮合的不平稳,其动态传递误差有明显的波动,随后在约0.001s(主动轮转过0.02rad)后传动进入平稳阶段。
对比动态传递误差和静态传递误差可知,在啮合平稳阶段此工况条件下的动态传递误差略小于静态传递误差,而其变化趋势基本一致。但是由于有限元分析过程中接触对设置的不同,以及齿轮副动态传递误差受到惯性、摩擦力、阻尼等因素影响,动态传递误差需进行进一步分析。

图8 环面渐开线齿轮动态传递误差
5 结语
由于环面渐开线齿轮齿面的复杂性,为了精确得到齿轮副的传递误差,在有限元软件中精确法建立了环面齿轮模型,通过非线性静力学分析得到了其静态传递误差,通过非线性隐式动力学分析得到其动态传递误差。通过分析得到如下结论:
通过赫兹接触理论的计算验证了齿面渐开线齿轮静力学分析数据的可靠性。在环面渐开线齿轮啮合过程中,在双齿啮合区啮合刚度大,弹性变形较小,此时静态传递误差较小;在单齿啮合区,啮合刚度小,弹性变形较大,此时静态传递误差较大。通过对不同转矩下静态传递误差的分析,表明在一定范围内,随着转矩的增大,该参数环面渐开线齿轮的静态传递误差线性增大,其相对传递误差也增大。
文章还基于非线性隐式动力学分析计算了一种工况条件下环面渐开线齿轮副的动态传递误差,结论表明在该工况下,动态传递误差与静态传递误差非常接近。
[1] 刘雷,黄因慧,田宗军,等. 一种凹、凸环面渐开线齿轮及其设计、加工方法:中国, 专利201210081587.4[P]2012-03-26.
[2] 曹涛. 新型环面渐开线齿轮齿面生成与啮合特性研究[D].南京:南京航空航天大学,2014:5-6.
[3] J. Derek Smith. Gear Noise and Vibration [M]. 2nd ed. New York-Basel: Marcel Dekker Inc., 2003:2-11.
[4] Tharmakulasingam R. Transmission error in spur gears: Static and dynamic finite-element modeling and design optimization[D]. United Kingdom: Brunel University,2009:105-153.
[5] 唐进元. 齿轮传递误差计算新模型[J]. 机械传动, 2008, 32(6):13-14.
[6] 白玉田, 任博文. 基于变刚度的齿轮传递误差计算[J]. 大众汽车, 2014(6):56-57.
[7] 张义民, 杨健, 胡鹏. 斜齿副传递有限元误差分析[J]. 机械设计与制造, 2014(3):189-191.
[8] 汪中厚, 王杰, 王巧玲,等. 基于有限元法的螺旋锥齿轮传动误差研究[J]. 振动与冲击, 2014(14):165-170.
[9] 张涛, 吴勇军, 吴静,等. 制造误差影响齿轮副啮合的接触有限元分析方法[J]. 振动与冲击, 2015(3):43-50.
[10] 江丙云,孔祥宏,罗元元. CAE分析大系:ABAQUS工程实例详解[M]. 北京:人民邮电出版社, 2015:129-130.
