基于ABAQUS强度折减法的边坡稳定性分析
2018-07-04杜聪
杜 聪
(广东晶通公路工程建设集团有限公司,广东 广州 510635)
工程界和学术界一直非常关注边坡稳定性分析的研究,把边坡稳定性分析和评价作为边坡工程的重点问题。在极限平衡法等边坡稳定性的研究理论出现之前,工程类比法是边坡稳定性分析中应用得较多的方法,但这种方法有很大的局限性,其类比的条件因地而异,而且根据经验人为地判定也存在着主观性,因此,判定的精度比较低。
20世纪20年代,Fellenius[1]等人建立了极限平衡法。随着研究的不断深入和发展,在极限平衡理论的基础上形成了多种边坡稳定性分析的方法。这些分析方法具有计算方便和模型简单等优点,适用于工程实践和研究工作。但是这些方法在某些方面也存在着不足,如:不能够考虑土体的本构关系;对边坡破坏的发展过程不能进行合理、有效的分析,往往需要靠一定的经验来确定滑动面。
将计算机技术与数值分析方法相结合,使岩土工程中许多复杂问题的研究和处理变得更加方便和精确。将有限元的强度折减法[2]与计算机技术相结合,使得用强度折减法能更好地运用于边坡稳定性研究中。作者拟运用有限元分析软件ABAQUS和强度折减法,以某高边坡为实例,研究边坡稳定性的相关问题。
1 强度折减法的原理
强度折减法最早由Zienkiewicz[3]等人提出,后被广泛采用。其基本原理是将边坡土体的2个参数(粘聚力c和内摩擦角φ)同时除以一个系数Fr进行折减,分别得到折减后的c′和φ′,然后,再将折减后的c′和φ′代入有限元进行试算。当计算至边坡达到极限状态时,对应的Fr即为边坡的稳定安全系数[4-5]。其计算式为:
c′=c/Fr。
(1)
φ′=arctan (tanφ/Fr)。
(2)
2 边坡失稳判断依据
对边坡失去稳定状态的判定依据有3种:① 以有限元数值计算是否收敛作为评价标准[6-7];② 以特征部位位移的突变性为判据[8];③ 以广义塑性应变或者等效塑性应变从坡脚到坡顶贯通作为边坡破坏的标志[9]。
一些学者指出,对边坡进行强度折减非线性有限元分析时,在数值计算不收敛情况下,不一定就表示边坡已经达到了不稳定状态[10],本构模型的选取、迭代的次数及收敛精度的规定均有可能使分析过程中出现不收敛的情况。单从不收敛是不能准确判断边坡已经失稳的。
对于边坡失去稳定的判定,许多学者在该研究领域进行了许多的研究,也取得了不少实质性的成果。但是,目前学术界在边坡稳定性的判定上还存在争议[11-13],对应于不同的情况下,这3类判定依据的适用性及这3类判据是否具有统一性的问题至今还未给出比较明确、统一的定论。但是,土体滑动面塑性区贯通其物理意义比较明确,在对边坡是否失稳进行判断时具有重要的参考价值。而边坡特征部位位移的突变对判定边坡失稳也有实际的意义。为了保证对边坡失稳情况判定的准确性,作者拟将塑性区贯通与特征部位位移的突变性结合起来,对边坡失稳进行判定。
3 工程实例分析
3.1 工程概况
3.1.1 边坡地质情况
某一岩质高边坡,坡高70 m,设计为7级边坡。根据现场勘察和调查,场内没有断层等不良地质现象,也不存在高液限土和膨胀土等不良土质体;根据地质勘察得知,边坡主要由全、强风化泥质粉砂岩和砂岩组成,中部夹杂有强风化炭质砂岩。从坡顶面向下依次为:全风化泥质粉砂岩、强风化砂岩、强风化泥质粉砂岩及中风化泥质粉砂岩,具体参数见表1。

表1 边坡岩土参数Table 1 Slope geotechnical parameters
3.1.2 边坡坡形及加固措施
边坡设计为七级边坡,几何模型如图1所示。其加固措施为:
1) 一级:边坡采用3排锚杆格梁加固,锚杆长8 m。格梁内喷混植生植草防护,其余坡面采用喷混植生植草防护;
2) 二、三级:采用4排预应力锚索框梁加固,锚索长22~24 m,锚固段长10 m。其余部分采用喷混植生植草防护。
3) 四、五、六级:全坡面采用人字形骨架植草防护。
4) 七级:客土喷播植草防护。
3.2 计算模型的建立
本研究将复杂的边坡简化为二维的面来考虑其稳定性,结合Mohr-Coulomb模型和线弹性模型来赋予边坡土体材料属性,运用非关联的流动法则进行分析。选择自由划分技术对网格进行划分,单元类型选为4节点平面应变单元。通过设置一个场变量[10]来实现强度折减法在ABAQUS中的应用。在ABAQUS的属性步骤中,设置材料参数时选用Mohr-Coulomb模型,并同时设置一个场变量(这里取为强度折减系数),将其设定在0.5~2之间线性变化,并根据场变量的变化,分别对应折减取得不同的粘聚力和内摩擦角,并将对应的参数输入。
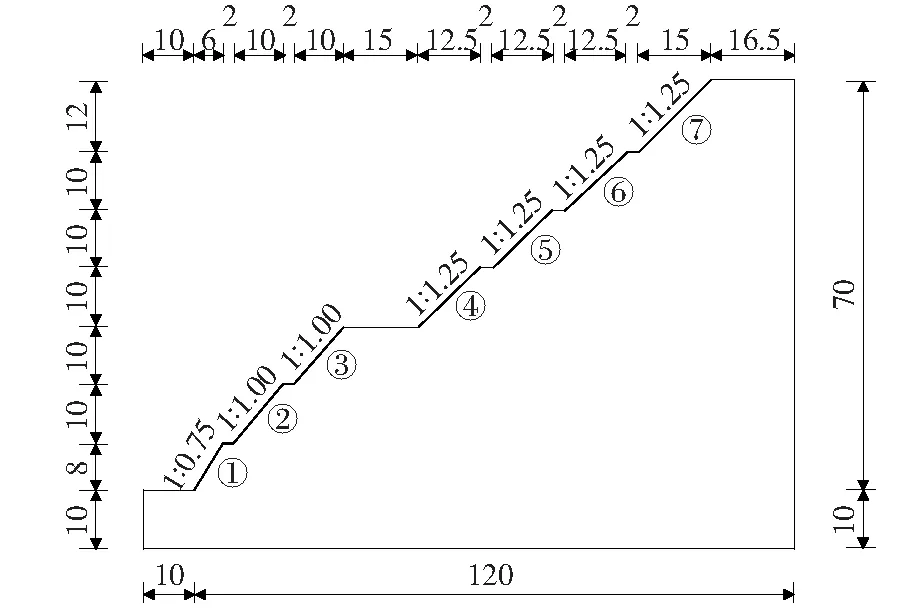
图1 边坡的几何模型(单位:m)Fig.1 The geometric model of the slope(unit:m)
3.3 结果与分析
本研究基于ABAQUS软件,以高边坡为例,对强度折减法分析边坡稳定性过程中的一些问题进行了分析和研究。
3.3.1 加固措施对边坡稳定性的影响
运用ABAQUS软件,分别模拟分析了高边坡加固前、后的状态,得出边坡加固前的安全系数为1.09(塑性区变形如图2所示),加固后的边坡稳定性安全系数为1.225。表明:加固措施对边坡稳定性的影响是很大的。加固前、后边坡水平方向的位移等值线云图分别如图3,4所示。从图3,4中可以看出,加固措施对于边坡水平位移的限制作用也是明显的。边坡在自然状态下不仅有自身重力荷载的作用,还要遭受降雨、甚至地震等其他因素的影响。这就需要采取加固措施,确保边坡的安全稳定。
3.3.2 强度折减法与极限平衡法的比较
运用Slide软件,并由简化Bishop条分法分析边坡在不采取加固措施情况下的稳定性,可得出边坡安全系数为1.08。表明:强度折减法对于边坡稳定性的分析是适用的。并且,有限元强度折减法不需要对滑动面的位置及形状作出相应的假定,而极限平衡法则需要先做假设。有限元强度折减法能求出边坡土体各点的应力、位移及破坏面和塑性区的变形。用有限元强度折减法分析会更加方便,它对于各种复杂形状、土质情况及非均质的边坡具有更好的适用性。
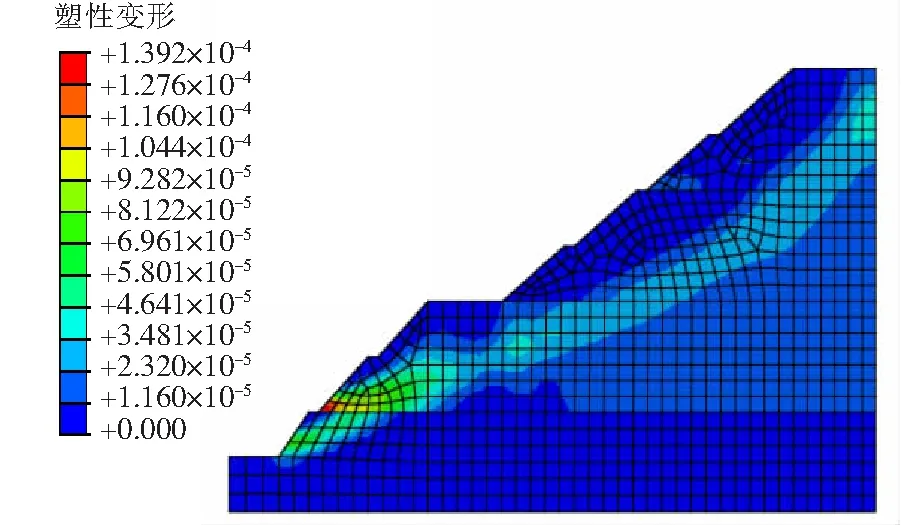
图2 未加固状态下Fs=1.09时的塑性区Fig.2 The plastic zone of Fs=1.09 in unreinforced state

图3 未加固状态下水平方向的位移等值线云图Fig.3 Displacement contour map in horizontal direction without reinforcement

图4 加固状态下水平方向的位移等值线云图Fig.4 Displacement contour map in the horizontal direction of the reinforced state
3.3.3 网格疏密对模拟分析的影响
网格的划分是有限元分析中比较重要的一环,单元的类型、网格划分技术及划分网格的数目和质量都会对模拟计算的精度产生影响。网格的疏密对计算精度的影响更加直观和明显。本研究以未加固状态下的边坡为例,划分不同密度的网格,分析网格疏密对模拟计算的影响(见表2)。从表2中可以看出,若是模型网格划分过于稀疏,则模拟分析出的安全系数会偏大,使得结果很不准确。在一定范围内,随着网格划分密度的提高,计算结果的精度也越高。但是,当网格密度提高到一定程度后,它对计算结果的影响就不明显了。如果再提高网格密度,反而会增加模拟计算的时间。

表2 网格疏密对模拟计算的影响Table 2 The influence of the grid density on the simulation
4 结论
运用大型有限元分析软件ABAQUS,并结合强度折减法,对高边坡稳定性的若干问题进行了探讨和研究,得出的结论为:
1) 加固措施对边坡稳定性的影响是非常明显的。在加固后,边坡的整体稳定性得到明显的提高,边坡的水平位移也得到了有效的控制。因此,对边坡进行加固处理十分重要,当然也要从经济方面考虑,选择合理的加固措施。
2) 有限元强度折减法对边坡稳定性分析具有较好的适用性。相对于极限平衡法,它更适用于复杂类型的边坡稳定性分析。
3) 在结合ABAQUS、运用强度折减法进行模拟分析时,模型的建立、网格的划分密度、单元类型的选取及材料模型的选用等都会影响计算结果,要进行合理的处理,以保证计算的精度。
4) 本研究边坡失稳是以特征点位移突变并结合塑性区贯通来判断的。但是,当前对于边坡的失稳破坏机理并没有形成广泛而统一的定论,值得进一步研究。
参考文献(References):
[1] 郑颖人.岩土数值极限分析方法的发展与应用[J].岩石力学与工程学报,2012,31(7):1297-1316.(ZHENG Ying-ren.Development and application of numerical limit analysis for geological materials[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(7):1297-1316.(in Chinese))
[2] Griffiths D V,Lane P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3):387-403.
[3] Zienkiewicz O C,Humpheson C,Lewis R W.Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique,1975,25(4):671-689.
[4] 郑颖人,赵尚毅,李安洪,等.有限元极限分析法及其在边坡中的应用[M].北京:人民交通出版社,2011.(ZHENG Ying-ren,ZHAO Shang-yi,LI An-hong,et al.FEM limit analysis and its application to slope engineering[M].Beijing:China Communications Press,2011.(in Chinese))
[5] 郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,10(4):57-61.(ZHENG Ying-ren,ZHAO Shang-yi,ZHANG Lu-yu.Slope stability analysis by strength reduction FEM[J].Engineering Sciences,2002,10(4):57-61.(in Chinese))
[6] 赵尚毅,郑颖人,时卫民,等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.(ZHAO Shang-yi,ZHENG Ying-ren,SHI Wei-ming,et al.Slope safety factor analysis by strength reduction FEM[J].Chinese Journal of Geotechnical Engineering,2002,24(3):343-346.(in Chinese))
[7] 赵尚毅,郑颖人,邓卫东.用有限元强度折减法进行节理岩质边坡稳定性分析[J].岩石力学与工程学报,2003,22(2):254-260.(ZHAO Shang-yi,ZHENG Ying-ren,DENG Wei-dong.Jointed rock slope stability analysis by strength reduction FEM[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(2):254-260.(in Chinese))
[8] Manzari M T,Nour M A.Significance of soil dilatancy in slope stability analysis[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(1):75-80.
[9] 赵尚毅,郑颖人,张玉芳.极限分析有限元法讲座——Ⅱ:有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2):332-336.(ZHAO Shang-yi,ZHENG Ying-ren,ZHANG Yu-fang.Study on slope failure criterion in strength reduction finite element method[J].Rock and Soil Mechanics,2005,26(2):332-336.(in Chinese))
[10] 刘金龙,栾茂田,赵少飞,等.关于强度折减有限元方法中边坡失稳判据的讨论[J].岩土力学,2005,26(8):1345-1348.(LIU Jin-long,LUAN Mao-tian,ZHAO Shao-fei,et al.Discussion on criteria for evaluating stability of slope in elasto-plastic FEM based on shear strength reduction technique[J].Rock and Soil Mechanics,2005,26(8):1345-1348.(in Chinese))
[11] 裴利剑,屈本宁,钱闪光.有限元强度折减法边坡失稳判据的统一性[J].岩土力学,2010,31(10):3337-3341.(PEI Li-jian,QU Ben-ning,QIAN Shan-guang.Uniformity of slope instability criteria of strength reduction with FEM[J].Rock and Soil Mechanics,2010,31(10):3337-3341.(in Chinese))
[12] 陈力华,靳晓光.有限元强度折减法中边坡三种失效判据的适用性研究[J].土木工程学报,2012(9):136-146.(CHEN Li-hua,JIN Xiao-guang.Study on the applicability of three criteria for slope instability using finite element strength reduction method[J].China Civil Engineering Journal,2012,45(9):136-146.(in Chinese))
[13] 费康,张建伟.ABAQUS在岩土工程中的应用[M].北京:中国水利水电出版社,2010.(FEI Kang,ZHANG Jian-wei.ABAQUS application in geotechnical engineering[M].Beijing:China Water & Power Press,2010.(in Chinese))
