增量形式背景的拓扑坍缩表示

张 涛,李和合,曹海兰,2,刘梦奇

1(燕山大学 信息科学与工程学院,河北 秦皇岛 066004)2(河北东软软件有限公司,河北 秦皇岛 066004)

1 引 言

形式概念分析[1]是对形式背景中的属性、对象及其间关系进行分析和研究的理论,其提供了一种与传统的、统计的数据分析和知识表示完全不同的方法.形式概念分析理论也称概念格理论,是由德国的WILLE教授于1982年根据概念的哲学思想所提出的一种数学方法[2,3].目前形式概念分析的应用领域已经越来越广泛,如软件工程[4],知识发现[5],数据挖掘[6]等.

形式背景的表示方法是该领域的研究热点之一.在经典的形式概念分析中,一般以Hasse图为代表的概念格对其进行表示.但概念格表示不但计算复杂,而且表示内容仅限于以概念为单位的数据结构.随后,以属性偏序关系为基础的属性偏序图[7]、以图计算为代表的属性树[8]、以Hasse图进行延展的直观图[9]以及以图论为基础的属性拓扑[10]等等表示方法应运而生.

属性拓扑 (Attribute Topology)是一种新型的形式背景的表示方法,其思想来源于计算机的网络拓扑结构.在属性拓扑中,将每一个属性看作是一个信息终端,则整个的形式背景表现为终端间的信息沟通拓扑结构[3].该结构可以通过加权图的形式进行直观展现,使其具有良好的可视化特性.目前属性拓扑在概念计算[11,12]、关联关系发现[13]、认知计算等[14]领域都已有所发展.在概念计算中,以属性拓扑为基础的概念计算方法主要包括串行概念分析[11]、并行概念分析[15]以及深度优先概念分析[12].但随着增量式计算的发展,迫切需要一种增量式的形式背景表示方法,为动态概念计算奠定表示基础.

属性拓扑的认知模型研究表明[14],对于特定新增对象,属性拓扑具有局部聚焦特性.因此,对于增量式认知计算任务而言,其只需要对增量相关部分进行聚焦,进行局部计算即可完成增量过程.本文即以局部聚焦特性为基础,提出拓扑坍缩算法(简称坍缩算法),并将其应用于增量式概念搜索,减少增量式概念搜索过程的复杂性,为基于认知模型的概念计算奠定基础.

2 属性拓扑的基本概念

一般情况下,增量式运算的增量部分在于形式背景中对象部分.因此需要将属性拓扑转化为对象拓扑表示.其基础定义如下:

定义1.一个形式背景可以表示为K=(G,M,I),其中,G表示形式背景中所有对象的集合,M表示形式背景中所有属性的集合,I⊆G×M表示对象与属性之间的关系,G×M表示集合G与集合M的笛卡尔积.

定义2.设K=(G,M,I)是一个形式背景,若A⊆G,B⊆M,定义一对算子

f(A)={m∈M|∀g∈A,(g,m)∈I}

g(B)={g∈G|∀m∈B,(g,m)∈I}

如果二元组(A,B)满足f(A)=B且g(B)=A,称二元组(A,B)是形式背景K中的一个形式概念.A称为概念(A,B)的外延,称为概念(A,B)的内涵.通常用B(G,M,I)或B(K)表示形式背景K=(G,M,I)的所有概念构成的集合.

在传统的属性拓扑表示中以属性为图的顶点,属性之间的耦合关系作为图的边进行表示.针对增量式计算一般为对象增量的情况,本文构造对象拓扑表示方法,将对象作为图的顶点,对象之间的耦合作为边进行表示.对象拓扑的定义为:

定义3.对于形式背景K=(G,M,I),对象拓扑的邻接矩阵表示定义为OT=(V,Edge).其中V=G,为对象拓扑的顶点集合,Edge为对象拓扑边的集合,称为该对象拓扑的邻接矩阵,Edge表示如下:

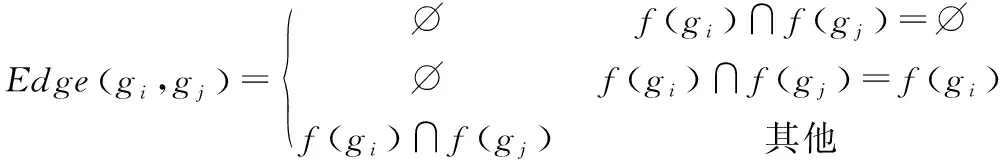
针对表1所示形式背景,其属性拓扑与对象拓扑分别如图1所示.

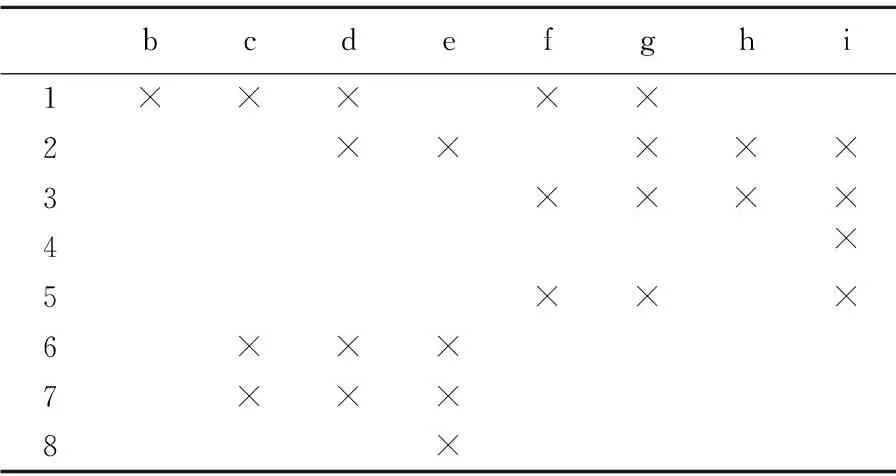
表1 形式背景Table 1 Formal context

由定义3和图1可知,对象拓扑实际上为形式背景K转置后的属性拓扑,二者具有内在的一致性.因此,可将属性拓扑中属性定义与定义引申至对象拓扑.

定义4.根据对象间的不同关系,可以将所有的对象分为顶层对象集合SupObj和伴生对象集合SubObj两个部分:

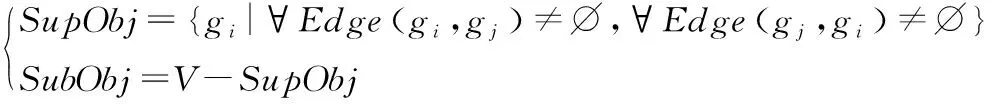
定义5.若存在gi,gj∈G,满足f(gi)⊂f(gj),则称对象gi和对象gj构成一组父子对象对,称对象gj为对象gi的父对象,记做gj=Par(gi);同时称对象gi为对象gj的子对象,记做gi=Chr(gj).

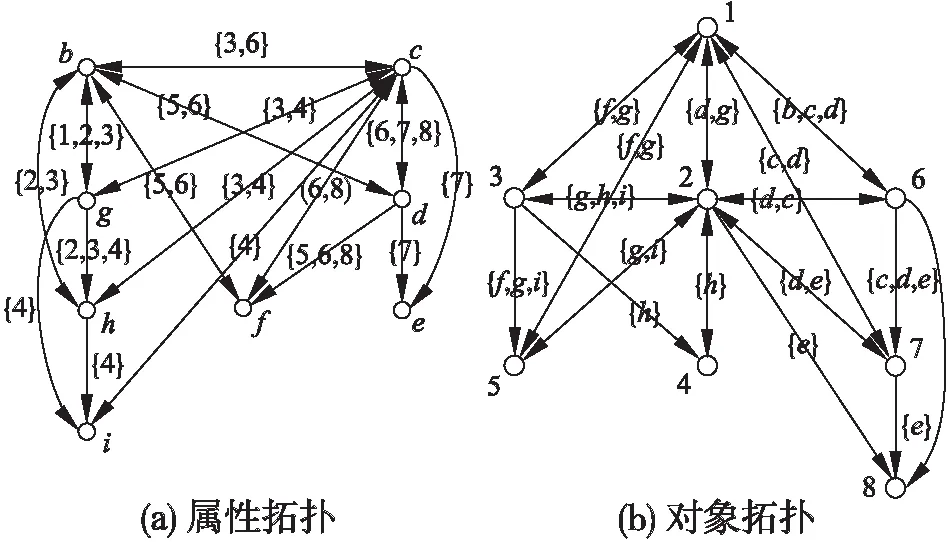
图1 属性拓扑与对象拓扑Fig.1 Attribute topology and object topology

3 对象拓扑的坍缩

人们在对新事物进行认知和决策时,会在大脑原有储备中进行激活或更新[16].若新增对象为已知对象时,可以直接完成对新增对象的认知.对未知对象的认知学习过程,可以通过类似证据的累积过程完成对其认知,该过程在对象拓扑中表现为增加未知对象对应的顶点与关联.随着认知过程的累积,对象拓扑或形式背景将变得越来越复杂,这将使未知对象的认知学习难于处理.为了降低对新增对象认知学习的复杂性,本文给出拓扑坍缩算法,简称坍缩算法.

对象拓扑的“坍缩”概念来源于天体物理学上物质在引力作用下坍缩形成黑洞过程.引力坍缩是恒星在自身物质的引力作用下彼此拉近而产生坍缩,从而自身向内坍陷的过程.将坍缩的概念引入到对象拓扑中,“坍缩”形象地表达了在原始形式背景所对应的对象拓扑基础上,通过对象间的相关性彼此吸引,从而向下一层坍陷的过程,坍缩过程简化和描述了对未知对象的认知学习过程,同时使对象拓扑的处理过程更加形象.

3.1 对象分类

在对象拓扑中,顶点之间的连线可以清晰地描述两个对象间的关系.对于一个确定的形式背景可以得到唯一的概念集合和概念格,因此一个确定的形式背景将对应于一个特定的认知能力.考虑到在形式背景中,新对象的加入不会影响原有各个对象之间的关系,因此在某个认知能力的基础上,实现对新增对象的认知,只需考虑新增对象与原有各个对象之间的关联性.

设原始形式背景为K=(G,M,I),加入新增对象new后的形式背景为K*=(G*,M*,I*),其中G*=G∪new,M*=M,I*⟺I;为了区分两个形式背景下的关系,将在形式背景K*下的算子记为fK*和gK*.

定义6.对于任意的新增对象new,根据新增对象与原有对象之间的关系,可以将新增对象分为三类:

1)若∃x∈G,使得f(x)=fK*(new),则称新对象new为已知对象.

2)若∀x∈G,满足f(x)∩fK*(new)=∅,则称新对象new为完全未知对象.

3)其它,则称对象new为半未知对象,根据对象间的具体关系可以细化为三种情况:

a)f(x)∩fK*(new)=f(x),对象new其特征可以覆盖在原始形式背景中对象x的特征,在对象拓扑图中,二者间存在由对象节点new指向节点x的单向边,且权值为f(x).

b)f(x)∩fK*(new)=fK*(new),在原始形式背景中存在对象x其特征包含对象new的特征,在对象拓扑图中,二者间存在由对象节点x指向节点new的单向边,且权值为fK*(new).

c)f(x)∩fK*(new)≠∅且f(x)∩fK*(new)≠f(x)且f(x)∩fK*(new)≠fK*(new),即二者为相容关系,在对象拓扑中,二者之间存在双向边,且权值为f(x)∩fK*(new).

根据定义6,若在现有的认知能力下,新增对象new与对象x的特征属性是相同的,则可以通过x完成对new的准确认识,将其划为已知对象;若新增对象与任意已知对象之间的关系呈现互斥关系,直观地看,在对象拓扑图中表现为二者间不存在任何边的连接,则新增对象new是一个完全陌生的未知对象.当new为半未知对象时,在原始形式背景中,存在与其关联的已知对象.由于在现有形式背景的认知能力下,无法直接明确的认识完全未知对象和半未知对象,将它们统称为未知对象.新增对象的各个类别之间的关系如图2所示.

图2 新增的对象各个类别之间的关系Fig.2 Relationship of new objects in the view of categories

例如,在表1的形式背景的基础上增加一个对象new1,其属性特征为{c,d,e},易得fK*(new1)=f(7),根据定义此时新增对象new1为已知对象,可以直接由对象7完成对新增对象new1的认知.若在表1所示形式背景的基础上新增对象new2,其属性特征为{d,e},易知新增对象new2为半未知对象,此时不能直接对new2作出准确的判断,且对象8与new2满足分类3中的条件a,对象2,6,7与new2满足分类3中的条件b,对象1与new2满足分类3中的条件c.

性质1.对于形式背景K=(G,M,I),设new为新增的未知对象,若#{fK*(new)}=1,则new与原形式背景K中对象只存在不关联关系和被包含关系.

证明:因为new为未知对象,所以不存在对象x∈G使得new=x.即若x∈G且#{f(x)}=1,则new与x定不存在关联.

当x∈G且#{f(x)}>1时,若f(x)∩fK*(new)=∅,则不存在关联;

若f(x)∩fK*(new)≠∅,则f(x)∩fK*(new)=fK*(new),即对象new与x为包含关系,且对象x包含对象new.

证毕.

3.2 坍缩过程

按照3.1小节给出的分类方法,新增对象可分为已知对象、完全未知对象和半未知对象,由于已知对象已经可以实现准确的认知,本节算法只针对后两种情形,讨论未知对象的对对象拓扑的影响.设未知对象为new,OT=(V,Edge)为原形式背景K所对应的对象拓扑,对象拓扑坍缩的算法见算法1,坍缩后所得对象拓扑记为OTclp=(Vclp,Edgeclp).

算法1.

算法名:对象拓扑的坍缩

算法功能:简化未知对象的增量式概念认知过程,减小新

增对象认知学习过程的复杂性.

Step1.Vur={v∈V|f(v)∩fK*(new)=∅}

Step2.OTct=(Vct,Edgect),Vct=V-Vur,

∀vi,vj∈Vct,Edgect(vi,vj)=Edge(vi,vj)

Step3.若新增对象new为顶层对象,则进入Step 4;否则

跳转到Step 6

Step4.令Vclp=Vct+{new},∀vi,vj∈Vclp,

Edgeclp(vi,vj)=

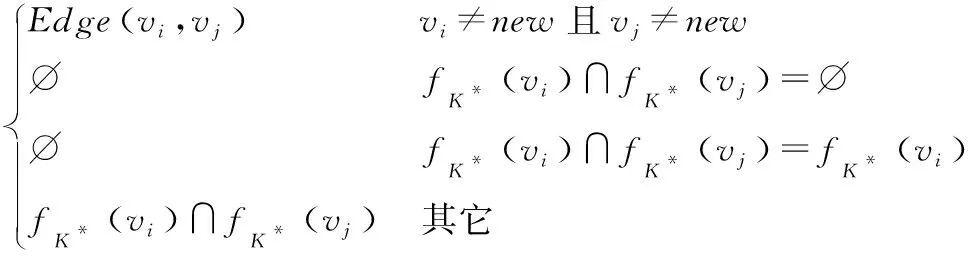
Step5.跳转到步骤7

Step6.令Vclp=Vct-Par(new)+{Par(new)∪new},

∀vi,vj∈Vclp

Edgeclp(vi,vj)=

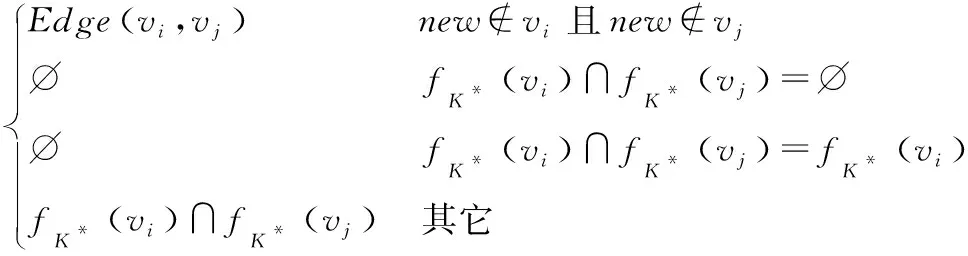
Step7.得到坍缩后的对象拓扑OTclp=(Vclp,Edgeclp)

在对象拓扑的坍缩过程中,Step 1-2根据新增对象new与原始对象拓扑OT=(V,Edge)中所有对象间的关联,对原始对象集合进行了分离,通过删除与新增对象new不存在关联的对象集合,得到规模较小的对象拓扑OTct.Step 3中将新增对象按顶层对象和伴生对象分别进行后续的坍缩算法.Step 4-7,完成对象拓扑的坍缩算法.对于新增对象为顶层对象的情形,将新增对象作为新结点加入,并依据对象间的关系完成对新增对象的认知.对于新增对象为伴生对象的情形,将新增对象与其父对象进行合并,然后再与原形式背景中各对象的对应关系,对其进行认知.对于完全未知对象而言,Vur=Vr,则OTct为一空拓扑,此时新增对象加入后成为拓扑中的顶层对象,算法转入Step 4-5,此时该对象将独立形成全新的概念,符合认知的原理.

对于表1所示的形式背景K=(G,M,I),对应的对象拓扑如图1(b)所示,若新增对象为new,满足fK*(new)={d,e}.直接在原始对象拓扑中进行表示,其结果如图3(a)所示.根据算法1对其进行拓扑坍缩运算,首先可以获得与新增对象无关的对象集合为Vur={3,4,5},然后获得对象拓扑OTct如图3(b)所示,其中Vct={1,2,6,7,8}.

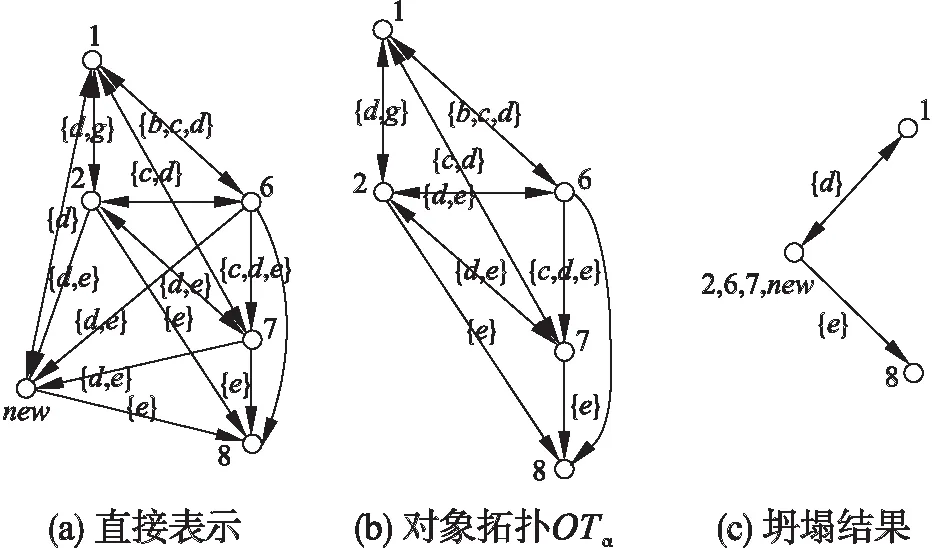
图3 坍缩过程示例Fig.3 Example of a collapsing process

可见,加入新增对象new后,完成对原始对象拓扑的坍缩时,若存在与对象new无关的节点,例如图3(a)所示的节点3、4、5,则通过坍缩可以去除掉原始对象拓扑的冗余部分,得到如图3(b)所示的OTct,此对象拓扑图仅与新增对象new存在关联性,是原始对象拓扑的子对象拓扑.

由于新增对象new满足fK*(new)={d,e},为一伴生对象,其父对象有{2,6,7},则将新增对象与父对象合并后可以得出Vclp=Vct-Par(new)+{Par(new)∪new}={1,2,6,7,8}-{2,6,7}+{2,6,7,new}={1,8,{2,6,7,new}}.此处为了描述方便,记NEW={2,6,7,new},则Vclp={1,8,NEW}.得到坍缩后的对象拓扑图3(c)所示.

4 实 验

为了验证本文提出的坍缩算法对增量式分析的影响,采用概念搜索算法对其性能进行评估.由于坍缩表示基础为属性拓扑,因此选择的对比算法均以属性拓扑为基础的DFFCS、BDAT两种算法.其中,DFFCS为典型的串行概念搜索算法,BDAT为典型的并行搜索算法.实验过程中均采用默认参数.

本节实验中选取5个数据集,除了典型的形式背景生物和水(Living Beings and Water)之外,还选取了四组来自UCI的数据集,Balance scale[17],Tic tactoc[18],Mushroom[19]和Nursery[20].这些数据集大多是多值的,因此实验前需要首先将它们转化为二值背景[1],然后经过预处理去除冗余的对象和属性,得到净化后的二值形式背景,实验中使用的各个二值形式背景的基本信息列于表2中.实验过程中采用的增量方式为按照数据集中默认对象顺序由零开始进行增量,至数据集中所有对象完成为止.

由于本实验主要考察坍缩运算对于运算速度的提升,因此以坍缩前后概念计算时间为评价指标.在进行实验时,考虑到算法的运行时间将会受到系统中其它进程的影响,为了减小实验的偶然误差,提高计算时间记录的准确性,每种算法分别对每个数据集进行了10次测试,最后对这10次记录的时间监视数据求取平均值,作为最终的算法运行时间.

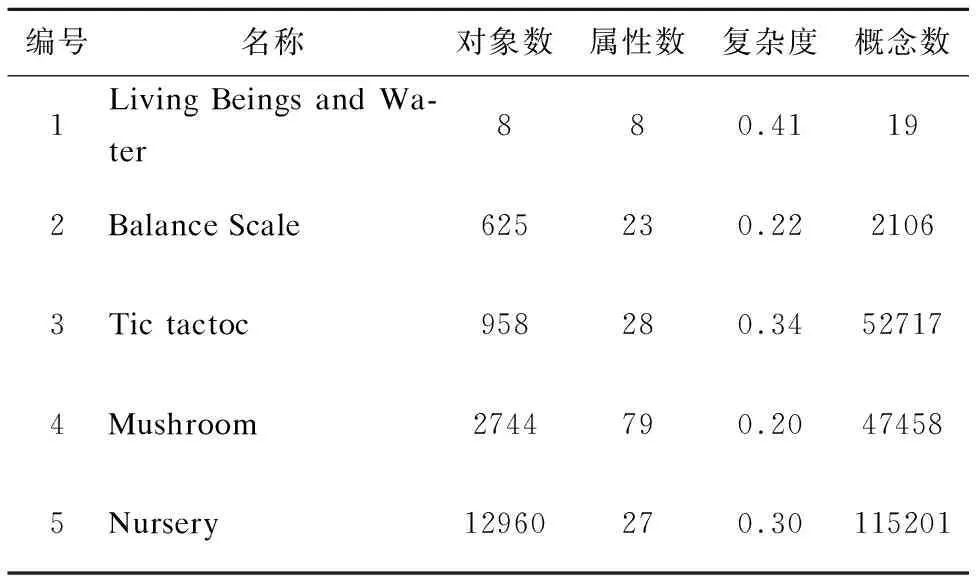
表2 实验中使用的二值形式背景的基本信息Table 2 Information of binary context in experiments

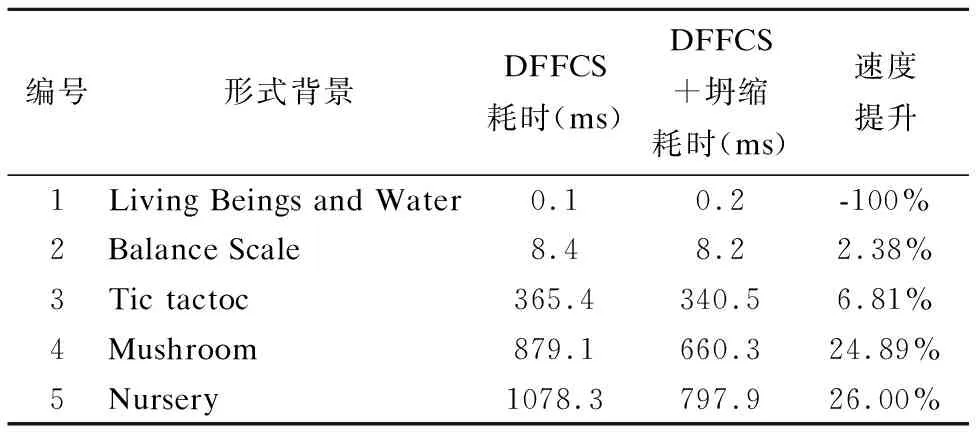
表3 DFFCS算法坍缩前后时间对比Table 3 Comparison before and after collapse to DFFCS intime consuming

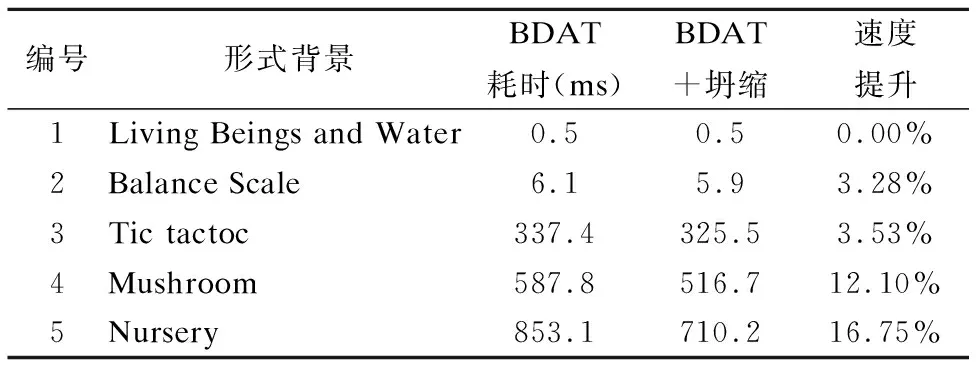
表4 BDAT算法坍缩前后时间对比Table 4 Comparison before and after collapse to BDAT in time consuming

综合表3和表4的实验结果,可以看到经过坍缩运算后的大多数增量式概念计算速度得到了有效提升.但对于串行计算而言,形式背景“Living Beings and Water”的运算时间反而有所增加.其原因在于该形式背景较小,坍缩运算的带来的计算量减小不足以抵消坍缩运算本身的时间消耗.但随着形式背景复杂度的增加,坍缩运算带来了明显的速度提升.因此,坍缩运算适用于中等规模以上的形式背景增量式分析.

通过对比表3和表4的实验结果,可以发现并行运算的速度提升低于串行运算.其主要原因在于本实验的增量方式为逐个加入.对于串行计算而言,坍缩后的串行表示方式仍维持较大规模,而并行运算经过分解后变为小规模形式背景.通过分析已知:小规模形式背景下坍缩运算对速度提升不如大规模形式背景明显.因此,并行运算的速度提升要低于串行运算.

5 结 论

本文在属性拓扑基础上,提出了拓扑坍缩的增量式形式背景表示方法.该表示方法可以直观的对新增对象进行聚焦表示,从而降低表示和后期计算的复杂度.实验表明,经过坍缩运算后的增量式概念计算,对于中等规模以上形式背景具有明显的速度提升.如何利用拓扑坍缩算法设计一体化的增量式概念搜索算法,是下一步值得研究的方向.

：

[1] Ganter Bernhard,Wille Rudolf.Formal concept analysis:mathematical foundations [M].New York:Springer-Verlag,1999:5-75.

[2] Ma Yuan,Zeng Zi-wei,Chi Cheng-ying,et al.Formal concept andits new development[M].Beijing:Science Press,2011:1-60.

[3] Xu Wei-hua,Li Jin-hai,Wei Ling,et al.Formal concept analysis:theory and application[M].Beijing:Science Press,2016:206-239.

[4] Sun Xiao-bing,Li Yun,Li Bi-xin,et al.A survey of using formal concept analysis for software maintenance[J].Acta Electronica Sinica,2015,43(7):1399-1406.

[5] Shao Ming-wen,Yang Hong-zhi,Wu Wei-zhi,et al.Knowledge reduction in formal fuzzy contexts[J].Knowledge-Based Systems,2015,(73):265-275.

[6] Rodríguez-Jiménez Jose Manuel,Cordero Pablo,Enciso Manuel,et al.Data mining algorithms to compute mixed concepts with negative attributes:an application to breast cancer data analysis[J].Mathematical Methods in the Applied Sciences,2016,39(16):4829-4845.

[7] Hong Wen-xue,Luan Jing-min,Zhang Tao,et al.Knowledge discovery method based on partial order structure theory[J].Journal of Yanshan University,2014,38(5):394-402.

[8] Zhang Tao,Hong Wen-xue,Lu Jing.Attribute tree representation for formal context[J].System Engineering Theory & Practice,2011,31(S2):197-202.

[9] Wei Ling,Wan Qing.Granular transformation and irreducible element judgment theory based on pictorial diagrams[J].IEEE Transactions on Cybernetics,2014,46(2):380-387.

[10] Zhang Tao,Ren Hong-lei.Attribute topology of formal context [J].Journal of Chinese Computer Systems,2014,35(3):590-593.

[11] Zhang Tao,Ren Hong-lei,Hong Wen-xue,et al.The visualizing calculation of formal concept that based on the attribute topologies [J].Acta Electronica Sinica,2014,42(5):925-932.

[12] Zhang Tao,Li Hui,Hong Wen-xue,et al.Deep first formal concept search[J].The Scientific World Journal,2014,2014(8):275-679.

[13] Zhang Tao,Wei Xin-yu.Association rules detecting based on attribute topology[J].Journal of Chinese Computer Systems,2017,38(3):548-552.

[14] Wei Xin-yu,Zhang Tao,Bai Dong-hui.Attribute topology granular analysis based on topology split[J].Journal of Chinese Computer Systems,2016,37(8):1751-1754.

[15] Zhang Tao,Bai Dong-hui,Li Hui.Parallel concepts computing based on bottom-up decomposition of attribute topology[J].Journal of Software,2017,28(12):3129-3145..

[16] Kvam Peter D,Pleskac Timothy J,Yu Shu-li,et al.Interference effects of choice on confidence:quantum characteristics of evidence accumulation [J].Proceedings of the National Academy of Sciences of the United States of America,2015,112(34):10645-10650.

[17] Gharehchopogh Farhad Soleimanian,Khaze Seyyed Reza.Data mining application for cyber space users tendency in blog writing:a case study[J].International Journal of Computer Applications,2013,47(18):40-46.

[18] Klahr David,Siegler Robert S.The representation of children′s knowledge[J].Advances in Child Development & Behavior,1978,(12):61-116.

[19] Lincoff Gary H.The audubon society field guide to north American mushrooms[M].Knopf:Distributed by Random House,1981.

[20] ZupanBlaz,Bohanec Marko,Bratko Ivan,et al.Machine learning by function decomposition[C].Proceedings of the Fourteenth International Conference on Machine Learning,1997:421-429.

附中文参考文献：

[2] 马 垣,曾子维,迟呈英,等.形式概念及其新进展[M].北京:科学出版社,2011:1-60.

[3] 徐伟华,李金海,魏 玲,等.形式概念分析理论与应用[M].北京:科学出版社,2016:206-239.

[4] 孙小兵,李 云,李必信,等.形式概念分析在软件维护中的应用综述[J].电子学报,2015,43(7):1399-1406.

[7] 洪文学,栾景民,张 涛,等.基于偏序结构理论的知识发现方法[J].燕山大学学报,2014,38(5):394-402.

[8] 张 涛,洪文学,路 静.形式背景的属性树表示[J].系统工程理论与实践,2011,31(S2):197-202.

[10] 张 涛,任宏雷.形式背景的属性拓扑表示[J].小型微型计算机系统,2014,35(3):590-593.

[11] 张 涛,任宏雷,洪文学,等.基于属性拓扑的可视化形式概念计算[J].电子学报,2014,42(5):925-932.

[13] 张 涛,魏昕宇.属性拓扑关联规则发现[J].小型微型计算机系统,2017,38(3):548-552.

[14] 魏昕宇,张 涛,白冬辉.基于拓扑分裂的属性拓扑粒结构分析[J].小型微型计算机系统,2016,37(8):1751-1754.

[15] 张 涛,白冬辉,李 慧.基于属性拓扑的并行概念计算算法[J].软件学报,2017,28(12):3129-3145.