基于核心素养的向量建模复习课*
2018-07-03
●
(华维外国语学校,浙江 绍兴 312300)
高三,是学生冲刺高考的备考阶段,是查漏补缺、复习巩固的最后机会.然而数学难,是学生共认的,难在知识点的理解,难在知识点的融合,难在题目的变形,难在解题方法的千变万化和思维要求之高,等等.在数学高考中如何争取更多的分数,决定了高考整体的成败,作为数学教师,肩上承担了“如何提升学生的数学解题能力”的责任.课堂是学生学习数学的主要阵地,课堂教学是教师“传道授业解惑”的主要方式,如何提高课堂教学的效度,变“授学生以鱼”为“授学生以渔”,是每个数学教师必须思考的实际问题.
核心素养,是近几年提出的对高中学科教学的综合性教学目标.数学核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析,全面概括了高中数学的教学核心目标,体现了学生的数学综合素养.
基于数学核心素养,教师应着重对学生的知识结构的形成与建立、对课堂知识的展示与巩固、对解题思路的引导与激发进行爆破性梳理.在此基础上对学生的知识理解和应用进行突破和引导,提升学生解决数学问题的能力高度.本文重点基于“数学抽象”,形成“直观想象”,明确“数学建模”,对高考数学复习中的向量问题进行系统性解惑.
1 向量建模之点到直线的距离
数学的基本思想是“抽象”,即抽丝剥茧,舍弃问题的物理属性,从中得到问题的研究对象,抓住数学本质,把概念与概念间的联系直接转化为解题的思路.
|b-ta|(其中t∈R)初看之下就是求某个向量的模长,如果学生采用两边平方就会陷入计算的麻烦.事实上从几何意义的角度看:若a与b起点相同,则|b-ta|(其中t∈R)就是求b的终点到a所在直线上点的距离,这样的模型建立使得求|b-ta|(其中t∈R)的最小值简单易懂.
例1已知共面向量a,b,c满足|a|=3,b+c=2a,且|b|=|b-c|.若对每一个确定的向量b,记|b-ta|(其中t∈R)的最小值为dmin,则当b变化时,dmin的最大值为
( )
A.0 B.2 C.4 D.6
(2017年浙江省台州市数学质量调测试题第10题)

图1
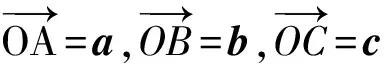
OB=BC,
即
(rcosθ+3)2+r2sin2θ=4r2,
整理得
r2-2rcosθ-3=0,
于是
而|b-ta|(其中t∈R)的最小值为dmin,则
因此dmin的最大值是2.故选B.
2 向量建模之三角形
向量的加法、减法与三角形有着天然的联系,我们可以利用三角形中的几何关系来简化向量的运算,实现快速解题.提到三角形,学生会想到:三角形的边长关系、正(余)弦定理等,有时候甚至延伸到平行四边形.这些均为简洁有效的解题方法,而解题关键是如何找到问题知识与解题方法之间的联系,建构正确的思维框架,最后解决问题水到渠成.

图2
例2已知平面向量α,β(其中α≠0,α≠β)满足|β|=1,且α与β-α的夹角为120°,则|α|的取值范围是______.
分析利用题设条件及其几何意义,构造三角形即可迎刃而解.本题主要考查平面向量的四则运算及其几何意义,突出考查问题的转化能力和数形结合的能力.

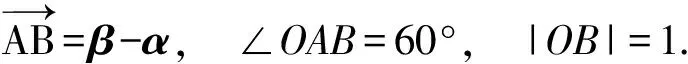
从而

3 向量建模之圆形
学生在初中阶段就详细具体地学习过圆,因此圆对高三学生来说是比较容易建立的模型之一,而且在高中解析几何教学中,又给圆插上了坐标的翅膀.当两个向量垂直(或者夹角为定值)时,我们可以直接构造圆来求解,特别是求某个量的范围时,可以采用坐标法进行数据处理.
例3已知平面向量a,b满足|a|=|b|=a·b=2,且(a-c)·(b-c)=0,则|b+c|的最大值为______.
(2017年浙江省绍兴市上虞区二模数学试题第16题)

图3
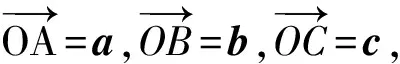
4 向量建模之面积
空间的“直观想象”体现了学习者的数学素质.根据待解决的问题,借助几何直观和空间想象能够感知问题的形式与变化,利用图形相连来描述数学问题,利用图形相通来分析数学问题,构建有效的直观数学模型来解决数学问题,提升学生数形结合的能力,培养创造性和转化性思维.
在向量题中,面积类问题在高考模拟卷中是新出现的题型.它集中了向量数量积的概念、三角函数、点到直线的距离等知识点,属于向量中的综合类题型,对学生的思维要求较高,不仅需要扎实的基础知识,还需要知识间的融会贯通.
例4已知平面向量a,b,c满足|a|=4,|b|=3,|c|=2,b·c=3,则(a-b)2(a-c)2-[(a-b)·(a-c)]2的最大值为
( )
(2017年浙江省绍兴市柯桥区二模数学试题第9题)
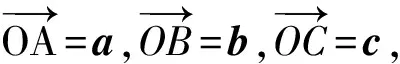

从而(a-b)2(a-c)2-[(a-b)·(a-c)]2=
BA2·CA2-(BA·CA·cos∠BAC)2=
(BC·h)2,
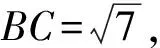
5 向量建模之空间图形
历年浙江省数学高考中,向量一直以平面向量的形式呈现,而且在实际教学中,空间向量往往是一种解决立体几何问题的工具,并不单独考查.2015年浙江省数学高考理科试题第15题,很多考生未能成功破解的主要原因:除题目本身具有一定的思维难度之外,关键是没有关注到该题考查的是“空间”向量还是“平面”向量,进而影响到构造的是平面图形还是空间图形.

(2015年浙江省数学高考理科试题第15题)
6 向量建模之综合题型
综合题型是考查向量的最高层次,融合了各种与向量有关的元素:三角形、圆形、三角函数、坐标、最值等,考查学生图形处理、数据运算、逻辑推理等数学核心素养,对学生数学思维的训练和解题能力的提升具有相当重要的作用.
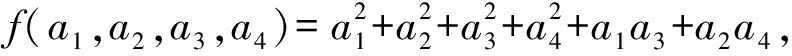
( )
(2017年嘉兴市第一中学、杭州高级中学、宁波效实中学等五校第二次联考数学试题第10题)

f=|m|2+|n|2+m·n,
从而
利用三角函数的有界性,得
7 几点反思
反思1向量是高中数学中重要的数学概念和数学工具之一,是数形结合的一个典范,代数问题几何化、几何问题代数化等多角度思维,是向量问题的特点.
反思2对于数学核心素养而言,向量几乎涵盖了核心素养的所有方面,包括抽象、推理、建模、想象、运算和分析,概括了高中数学的教学核心目标,考查了高中学生的数学核心思维,体现了思考分析、数学建模等核心能力.
反思3向量教学应着重对知识结构的形成与建立进行有效引导,教师应对课堂知识的理解与巩固进行有效指导,对解题思路的分析与突破进行有效向导,努力做到“授人之渔”.
反思4在高考中显性的向量问题多以选择题和填空题的形式出现,可以利用数形结合来解决.但在实际解题中,能取得意外效果、达到“事半功倍”的往往是那些隐性的向量问题.


图4
1)求直线AP斜率的取值范围;
2)求|PA|·|PQ|的最大值.
(2017年浙江省数学高考试题第21题)
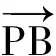
总之,对于向量问题,通过“抽象”,形成“想象”,正确“建模”,有利于提升向量复习课堂教学的针对性,提高学生解决向量问题的有效性.
