补形法在竞赛、自主招生、高考中的应用*

●

(学军中学,浙江 杭州 310012)

2018年浙江省数学竞赛刚落下帷幕就引发了很多的讨论.大多数人都认为此次的试题比较容易，甚至比2017年的还要容易些.笔者有幸参与了此次竞赛的阅卷工作，在结算总分的过程中，高分一个接一个地冒出来，这也从侧面说明了此次试题的难度不大.在这15个试题中，笔者对第10题情有独钟.

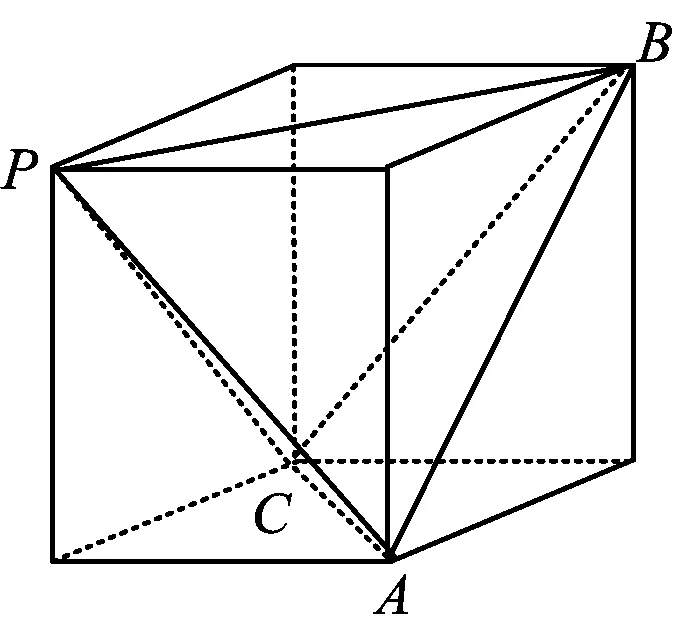
图1

解因为3组对棱都相等，所以考虑将四面体放入到长方体中(如图1).假设长方体的长、宽、高分别为x,y,z，则

由于四面体的外接球即为长方体的外接球，因此外接球的半径为

考后笔者询问了几个学生，想法也如出一辙，都将四面体放入了长方体.此解法用的是补形思想，即把四面体补成一个长方体.“补”和“割”都是数学中的重要思想，本文主要介绍补形思想在竞赛、自主招生以及高考中的一些简单应用.

1 补形法在竞赛中的应用

例2在四面体ABCD中，已知∠ADB=∠CDB=∠ADC=60°，AD=BD=3，CD=2，则四面体ABCD的外接球半径是______.

(2011年全国高中数学联赛试题第6题)

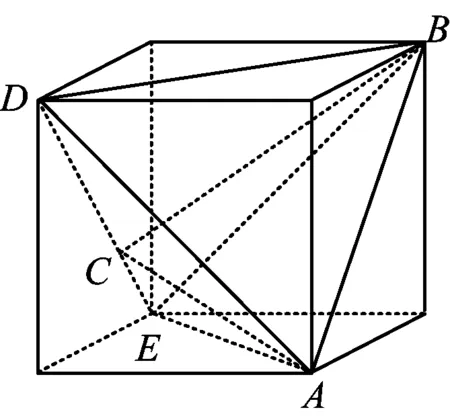
图2

解得

故外接圆半径为

这两个竞赛试题的共同点是通过适当的补形，将四面体放入长方体中，然后再加以解决.长方体，这个在小学阶段就已经接触到并非常熟悉的几何体，在高中阶段的立体几何中继续发挥着它巨大的作用.众所周知，在求正四面体(或一些特殊四面体)的体积、外接球半径时，我们都可以把该四面体放入长方体中来解决.那么哪些几何体能放入到长方体中呢？首先正四面体显然可以放入长方体中，那么任意一个3组对棱两两相等的四面体能否放入到长方体中呢？

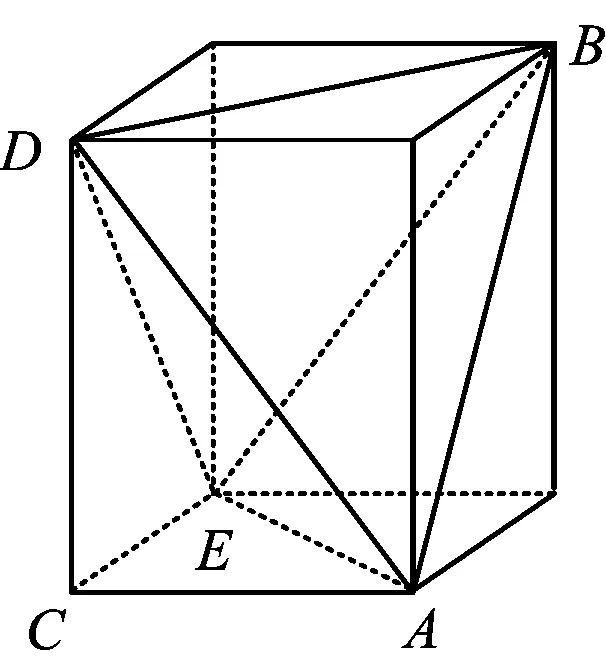
图3

结论13组对棱分别相等的四面体能放入长方体.

证明若四面体ABDE能放入一个长、宽、高分别是a,b,c的长方体中，则放入后的位置如图3所示.不妨设AC=a,CE=b,CD=c，则

2c2=m2+n2-s2,

2b2=s2+n2-m2,

2a2=m2+s2-n2，

从而只需证明m2+n2>s2，即只需证明∠ADE是锐角.易知∠BED=∠ADE,∠BEA=∠DAE，于是

∠BED+ ∠DEA+∠BEA=π>2∠BED=2∠ADE,

故存在a,b,c满足条件，即结论1成立.

此外还有一些比较规则的四面体也可以放入到长方体当中，如有一个顶点处是“墙角”的四面体，还有4个面都是直角三角形的四面体等等.

在这些四面体中，有一些保留了长方体的部分特点，容易让人联想到它们和长方体的关系，从而使问题迎刃而解；也有一些几何体，即使保留了长方体的部分特点，但是它与长方体之间的关系不容易被看出；还有一些几何体，长方体的大部分特点都被割去，这给我们解决问题带来了一定的困难.因此，笔者认为，这才是命题者的命题思想和命题背景.笔者顺着此命题思路，给出了两个变式.

图4

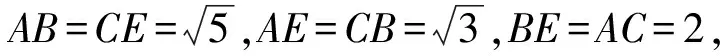
变式2在正四面体ABCD中，已知∠ADB=∠CDB=∠ADC=60°,AD=3,BD=1,CD=2,则四面体ABCD的外接球半径是______.

点评在变式2中△ABC不是正三角形，传统的方法不能奏效，但是补形的思想仍然可以使用.

相比例1和例2，这两个变式更能反映出补形思想的妙处.尽管这一类题目有一些难度，但是却受到了各大高校自主招生的青睐.

2 补形法在自主招生中的应用

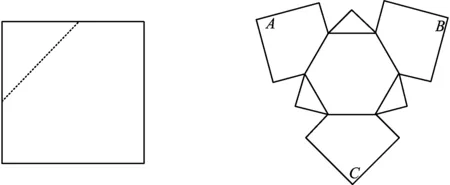
图5 图6

(2005年上海交通大学自主招生试题)

图7

点评该试题中的几何体保留了长方体的部分特点，但是不容易发现，可一旦发现之后，问题就很简单.此题若采用传统的方法求解，则要耗费不少精力，另外还需要比较强的空间想象能力和计算能力.但若考虑几何体与正方体之间的联系，则可以简化计算，达到事半功倍的效果.

3 补形法在高考中的应用

除了竞赛和自主招生外，补形法在高考中也有着一定的地位，例如2014年全国数学高考卷Ⅰ理科第12题，试题中的四面体割去了正方体的大部分特点，只留下了一些蛛丝马迹，若不利用正方体，要想象出几何体，会有一定的难度.

例4如图8，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为

( )

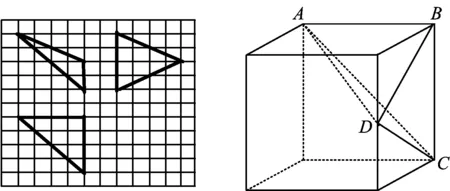
图8 图9

解由三视图可以判断，该几何体为四面体，且可以放入长方体中.设该四面体为A-BCD，则放入边长为4的立方体中的位置如图9所示.易知答案选B.

类似这样的补形思想，高考试题中还有很多,如：

例5已知直三棱柱ABC-A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为

( )

(2017年全国数学高考新课标卷Ⅱ理科试题第10题)

图10

解对直三棱柱ABC-A1B1C1进行补形,补成一个直四棱柱ABCD-A1B1C1D1(如图10)，易知答案选C.

例5是将三棱柱补成了一个平行六面体，再如例6将几何体补成了一个三棱锥，从而降低解题的难度.

例6如图11,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1，BC=2，AC=3.

1)求证：BF⊥平面ACFD；

2)求二面角B-AD-F的平面角的余弦值.

(2016年浙江省数学高考理科试题第17题)

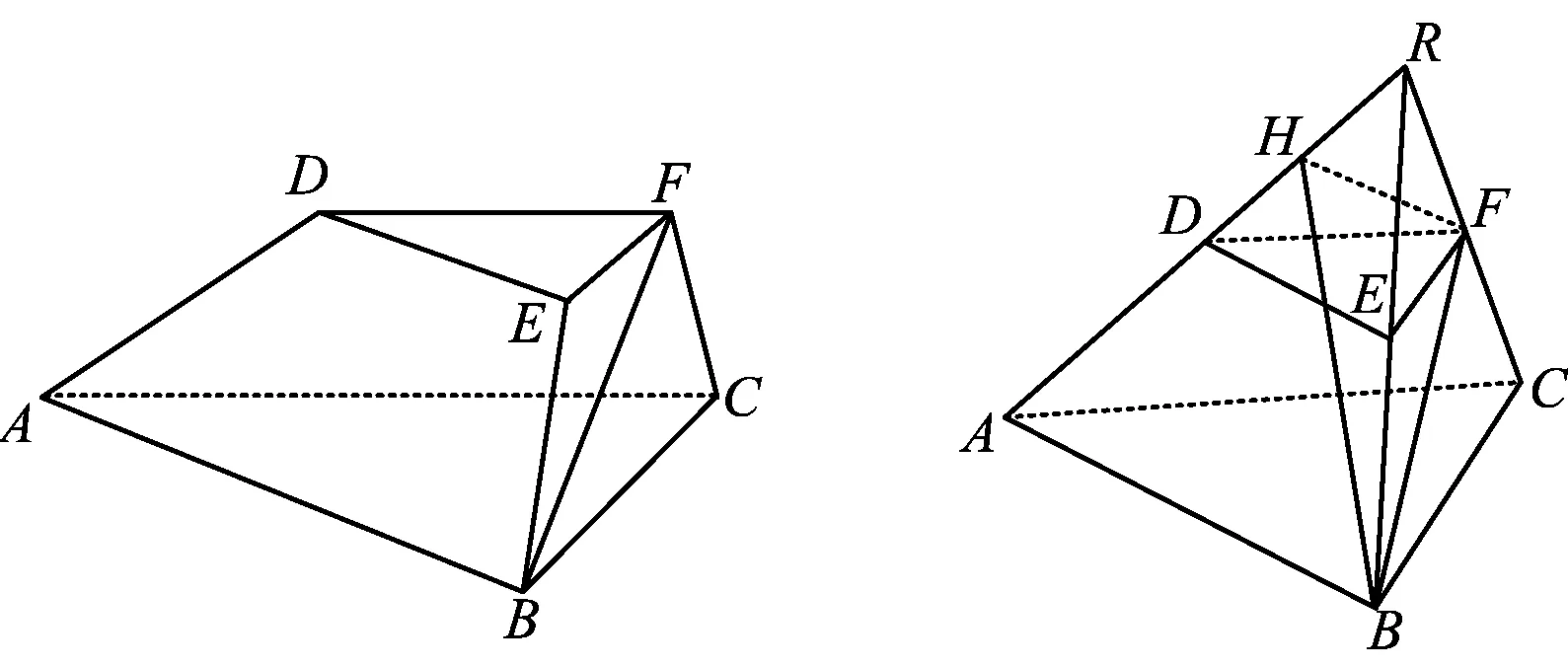
图11 图12

1)证明延长AD，BE，CF交于一点R(如图12).易证△BCR是正三角形，且F为中点，从而BF⊥CR.因为平面BCFE⊥平面ABC，∠ACB=90°，所以BF⊥CA，故BF⊥平面ACFD.

其他可以用补形法解决的高考试题还有很多，如2014年安徽省数学高考理科试题第20题、2017年全国数学高考新课标卷Ⅱ理科试题第19题.

4 感悟

补形作为一种基本的数学思想，无论是在竞赛、自主招生还是在高考中都是非常重要的，在平时的教学中都应有所提及.但是现实中，笔者发现很少有教师提到补形的思想，或者只在讲解类似的题目时，才会提及补形的思想.“割”和“补”是相对的两种手段，出题的时候用了“割”，做题的时候就用“补”，这就是补形.如果把补形后的几何体看作是“整体”，那么补形前的几何体就是“局部”，因此补形是一种站在“整体”的角度用俯视的眼光去解决“局部”问题的思想.

笔者认为能够用补形法来解决的问题，大致可以分为3类:1)几何体较为规则的且计算不麻烦，如例4和例5.此类几何体，不用补形法也可以计算，用补形法会更直接.2)几何体较为规则，但是不容易计算，如例1和例6.此类几何体因外形较规则，会让学生忘了用补形，是3类情况中相对比较难的一类，也是需要强调的一类.3)几何体不规则，如例2和例3，想到补形比较自然.

在用补形法解决问题时，大致可分为两步：首先，要找到合适的“整体”，即要找到被割之前的几何体，这应该是解答过程中最难的一点.有时候“整体”可以是长方体本身，也可以是那些可以放入到长方体中的特殊几何体，比如正四面体.当然还可以是其他的，比如棱台的“整体”可以是棱锥，再如四棱锥的“整体”可以是三棱锥.若有多个“整体”可以选择时，只需要选择一个方便计算的“整体”就可以了.在还原“整体”时，本文前面所阐述的几种类型的几何体都可以作为参考.然后，将几何体放入到“整体”中，根据几何体和“整体”的关系，求出所要求的结果.

总之，要用好补形思想，就必须清楚特殊几何体可能出现的各种“局部”问题，只有这样才能发挥补形思想的最大作用.