D-InSAR和水准数据融合方法研究

杨 帆，赵增鹏，张 磊，张子文(辽宁工程技术大学测绘与地理科学学院，辽宁 阜新 123000)

水准测量是传统的高程测量技术[1]，它具有精度高、成果可靠、仪器设备简单、技术容易掌握等优点，但只能得到有限个监测点的变形值。InSAR监测技术是20世纪后期发展起来的新兴交叉学科[2]。20世纪90年代，InSAR和D-InSAR技术得到了空前的发展并被广泛地加以应用[3]。国内对InSAR技术应用于地表形变监测的研究始于近年，且主要集中于城市地面沉降监测[4-5]。但其监测结果受多种误差源影响，沉降最大值附近精度较低。两种数据有很好的互补性，因此为全面利用监测数据，更加准确地描述地面沉降区域的沉降现状，可尝试应用数据同化的方法将D-InSAR监测值和水准监测数据进行融合。

数据同化是指在考虑数据时空分布、观测场和背景场误差的基础上，在数值模型的动态运行过程中融合新的观测方法，对监测的动态模型轨迹进行一定的约束，从而提高变量的估计精度。作为数据同化的一种新方法，集合卡尔曼滤波(ensemble Kalman filter，EnKF)近年来取得了显著的进展[6-7]，但是集合卡尔曼滤波在地面沉降监测多源数据融合中的应用在国内并不多见。本文提出一种基于集合卡尔曼滤波的D-InSAR和水准监测数据融合方法，使融合后的数据达到地面沉降监测数据的高空间分辨率与高高程变形精度的有效统一，使其更好地反映地面沉降区域的沉降规律，为地面沉降监测和预报提供数据上的支持。

1 融合方法

1.1 融合模型的建立

考虑水准监测数据比D-InSAR的处理结果更能真实地反映出地面沉降规律，在利用集合卡尔曼滤波进行D-InSAR值和水准监测数据融合的过程中，采用以水准监测数据为主的同化方式：根据观测的水准值，利用最小二乘拟合方法拟合出工作面的区域沉降值(反演值)；将反演值与D-InSAR值分别作为观测场和背景场代入到同化系统中，通过集合卡尔曼滤波同化算法融合D-InSAR值与反演值，并将同化结果与真实值相比较，从而判断数据同化方法融合数据的准确性和可靠性，将D-InSAR值与反演值经集合卡尔曼滤波计算得出融合结果。

同化系统的流程如图1所示。

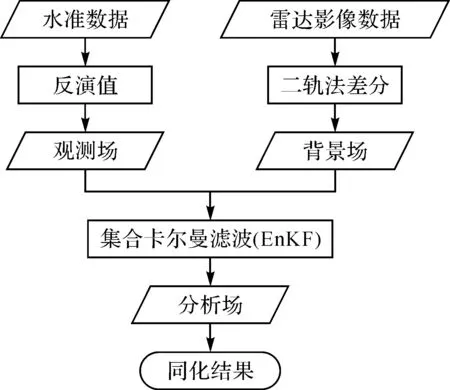
图1 同化系统流程

1.2 集合卡尔曼滤波原理

集合卡尔曼滤波由Evensen[8]于1994年最先提出并将其应用到海洋同化领域中。1998年，Houtekamer和Mitchell[9]首次在大气资料同化领域中使用了EnKF方法，后被广泛应用于大气预报领域[10]，主要由预测和分析两部分组成[11]。在集合卡尔曼滤波中，背景场由一组集合成员组成，通过对集合样本的统计实现卡尔曼滤波方程组中背景误差协方差矩阵的估计。它的基本流程为[12]：根据背景和观测的误差分布特征对背景场和观测场加扰，再通过统计集合扰动场得到背景误差协方差矩阵，进而得到分析方程中的增益矩阵，利用增益矩阵和分析方程，对背景集合进行分析，得到分析集合，继续向前预报[13]。

集合卡尔曼滤波最显著的特点为：误差协方差是通过对集合成员的分析统计得到的，具体的分析过程如下：

首先定义t时刻的背景场为

(1)

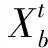
集合平均为

(2)

集合成员的扰动量定义为

(3)

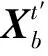
(4)

背景误差协方差为

(5)

假设观测是无偏的，定义观测向量为

(6)

式中，N为观测数；m为集合成员数。

基质由斜长石、橄榄石假象、单斜辉石组成，斜长石呈半自形板条状，长径一般0.03～0.2mm，杂乱似格架状分布，表面相对较干净，局部硅化；橄榄石、单斜辉石呈半自形—他形柱粒状，粒径一般<0.1mm，少数0.1～0.2mm，杂乱似填隙状分布于斜长石格架间，显间粒结构，橄榄石被皂石及少量硅质、碳酸盐交代呈假象，单斜辉石局部皂石化、碳酸盐化。岩内见少量碳酸盐充填的显微裂隙分布。

对观测扰动量定义如下

(7)

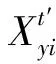
(8)

观测误差协方差矩阵根据观测扰动计算得到，定义如下

(9)

K为待定系数，也叫作Kalman增益矩阵，计算如下

K=BtHT(HBtHT+Ot)-1

(10)

在具体的计算中

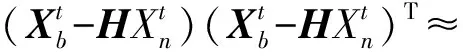
(11)

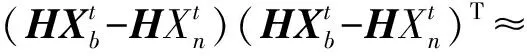
(12)

式中，i为集合成员数。集合卡尔曼滤波计算流程如图2所示。

2 实例验证

2.1 试验数据

本试验采用EnKF方法，结合河北省某矿区开采沉降监测数据，在等间隔时间序列观测值的基础上建模，进行了开采区域沉降变形的预测。

选取1326工作面为研究对象，选取2014-03-06至2016-05-18的D-InSAR与水准累计沉降监测数据进行试验。开采沉陷区概况和水准点布设情况如图3所示，监测点累计沉降监测数据见表1。

背景场误差均方差取0.01,观测场误差均方差取0.01。集合数m对预测值的精度有一定影响[14]。取值过大会影响计算速度，过小又会给系统带来统计误差[15]。为了兼顾计算精度和效率的平衡，本试验经过模拟不同集合数m，最终取m等于100，可达到计算精度和效率的最大化。

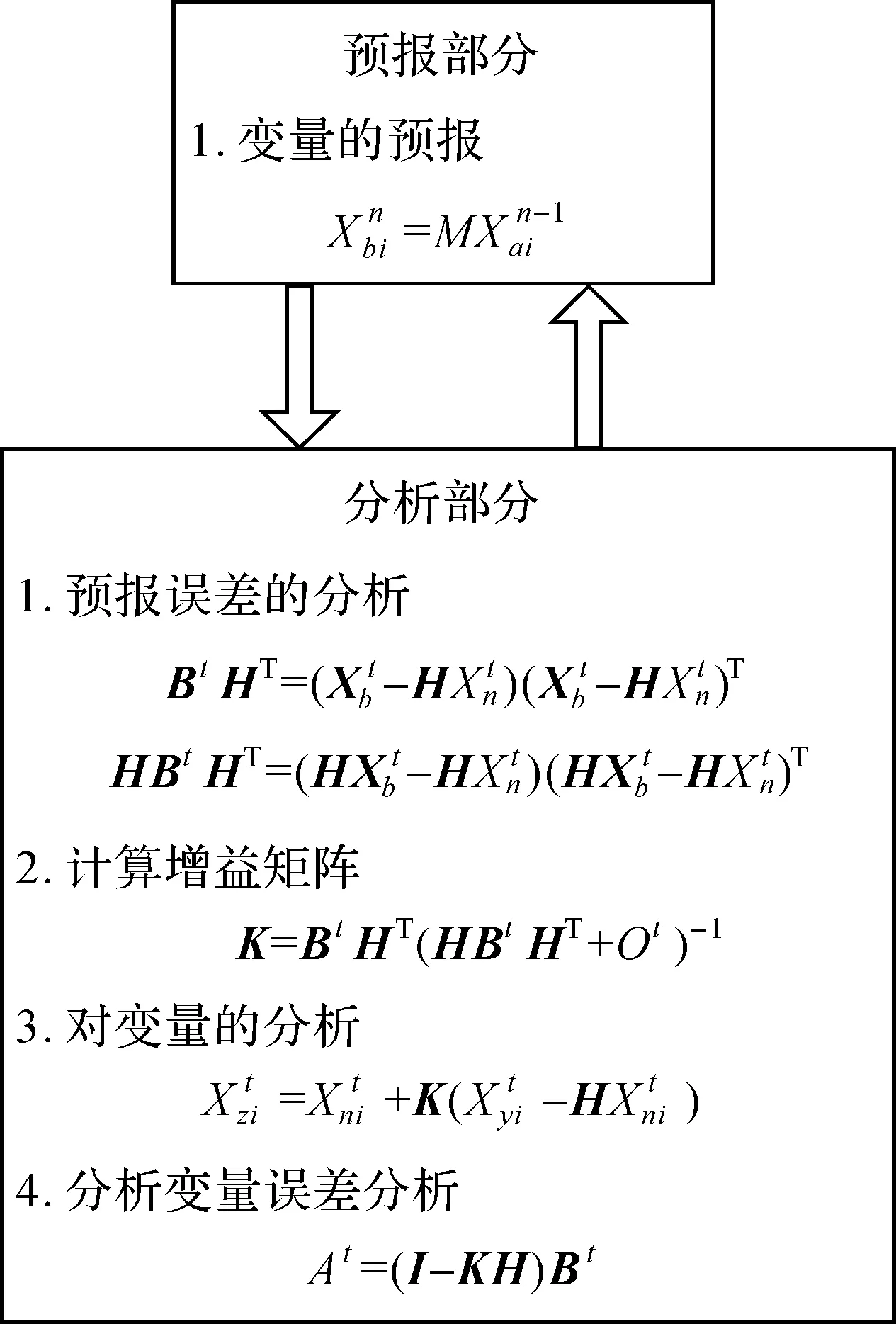
图2 集合卡尔曼滤波计算流程

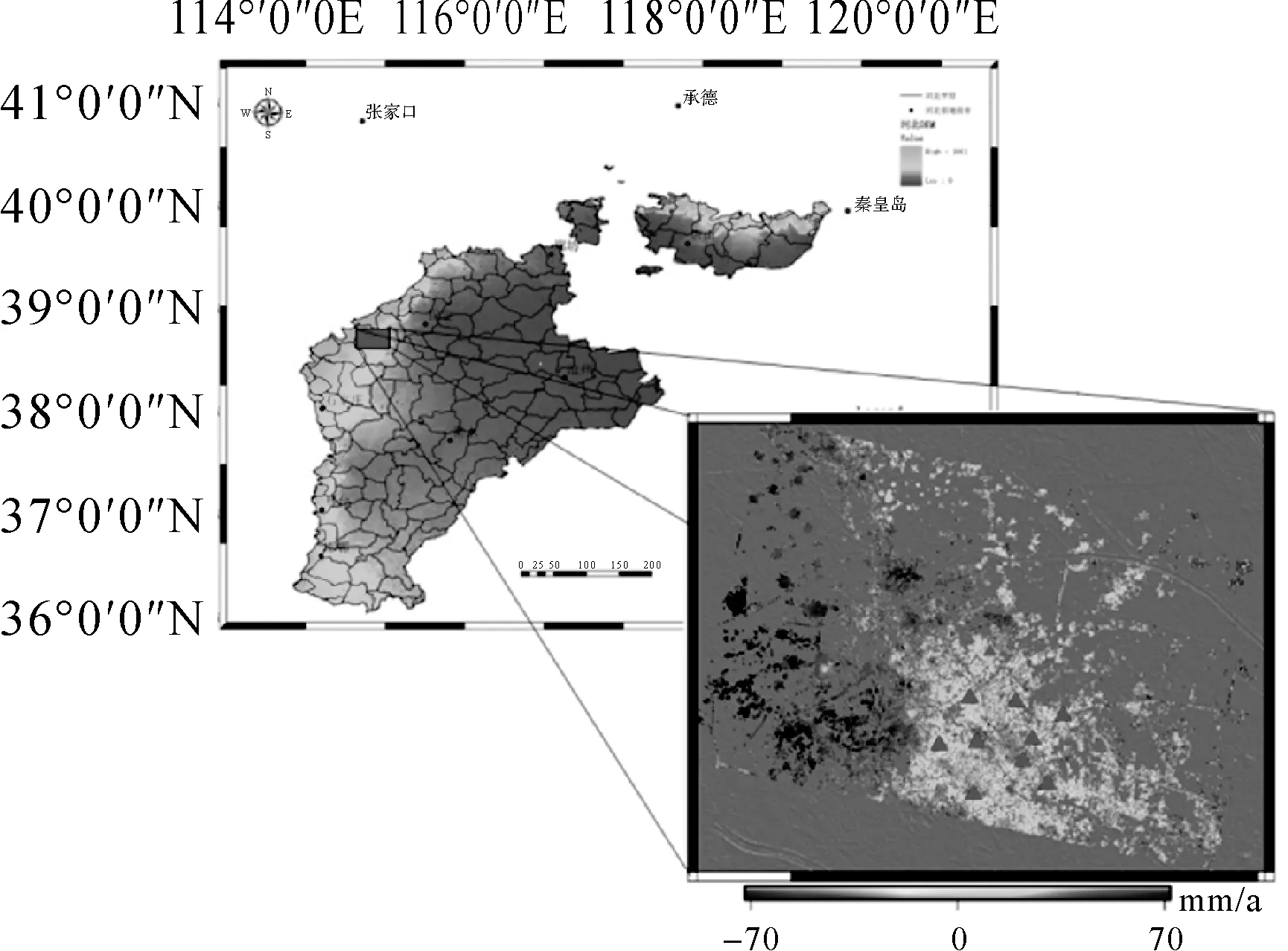
图3 工程概况

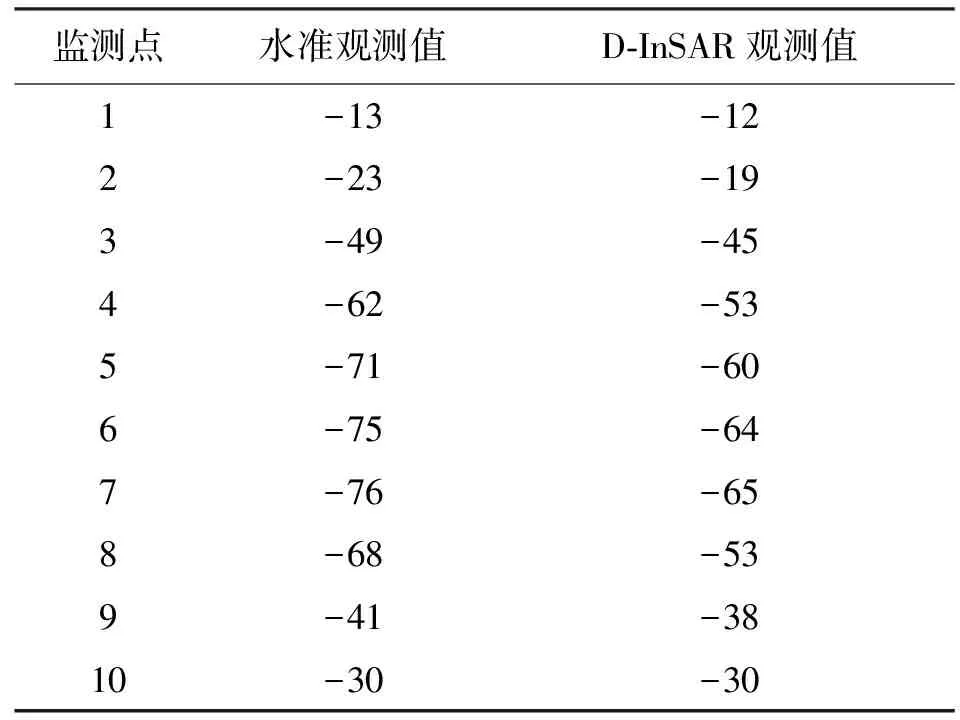
表1 监测点累计沉降量 mm

2.2 试验结果分析

基于表1的数据建立EnKF预测模型，并采用Matlab语言编程实现。数据同化结果对比展示如图4所示。

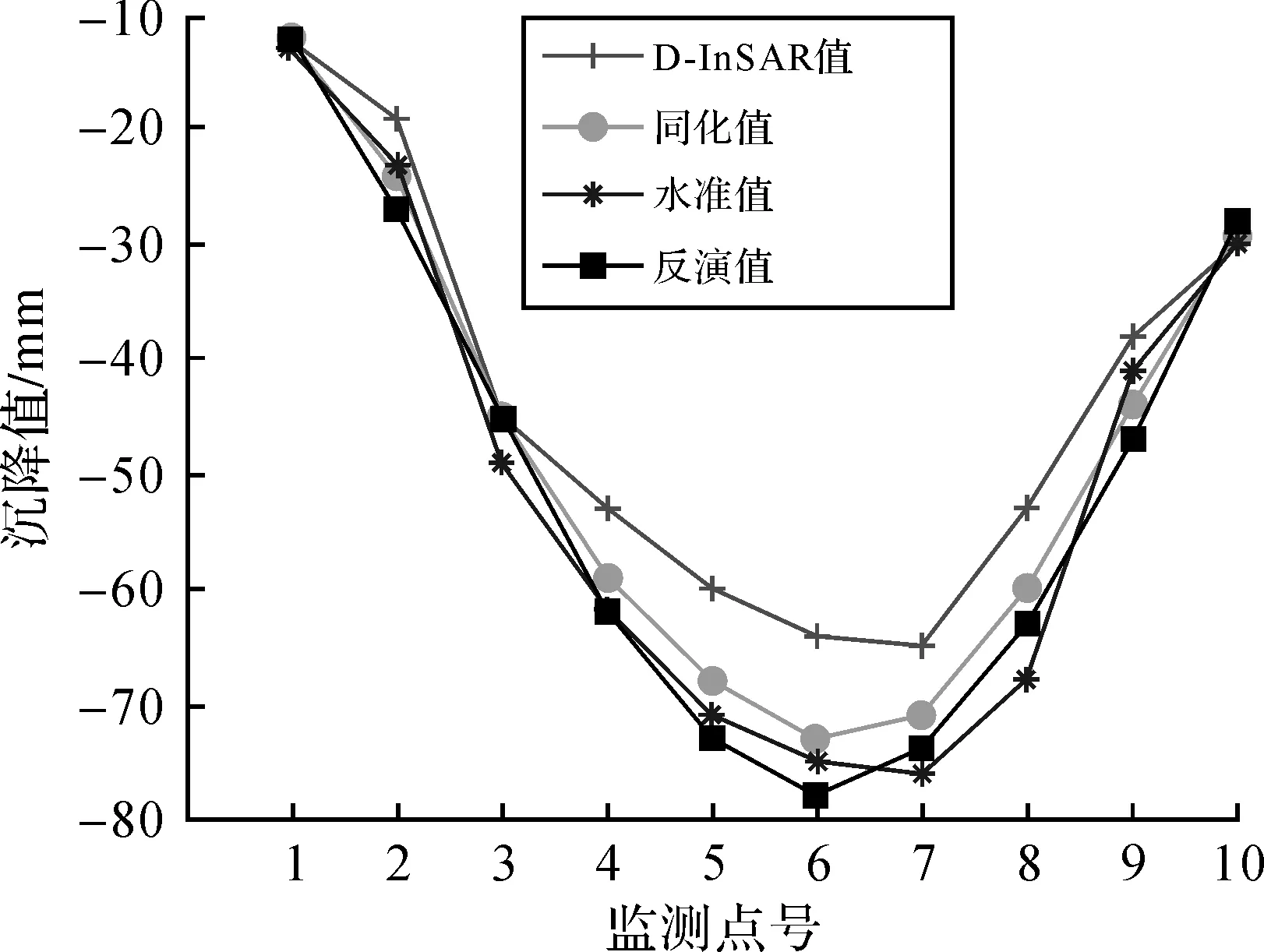
图4 数据同化结果对比

各监测点处D-InSAR值和同化值相对于水准值的误差如图5所示。

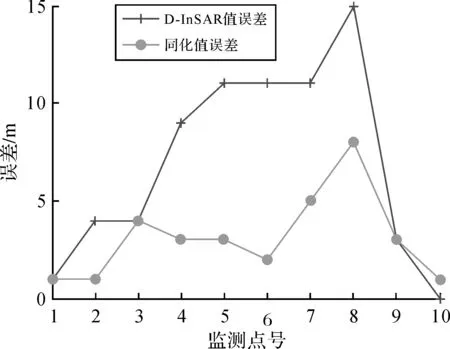
图5 误差对比

为了精确评价同化效果，选取ME(平均误差)、RMSE(均方根误差)和MRE(平均相对误差)3个指标对所得结果进行评价，计算公式为

(13)

(14)

(15)

精度评定结果见表2。

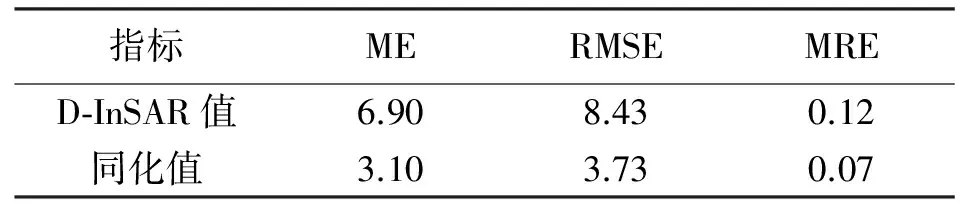
表2 监测点数据同化精度分析 mm

由图4可知，4种数据总体变化趋势一致，但呈现出一定的差别。反演值与水准值无论是在沉降盆地中心区域还是边缘区域差别都比较小；D-InSAR值与水准值中心区域差别较大，边缘区域差别较小；同化值结果处于两者之间，与D-InSAR值相比有了很大的改善，同化值能够较好地反映地面沉降区域的沉降特征。

由图5可知，D-InSAR值与水准值的误差基本在5 mm以上，而同化值与水准值的误差大体都在5 mm以下，D-InSAR值与水准值的误差远大于同化值与水准值的误差，从与水准值的误差大小来看，同化值的效果好于D-InSAR值。

由表2可知，在ME、RMSE和MRE 3个指标下，同化值的效果均好于D-InSAR值。同化值的平均误差为3.10 mm，均方根误差为3.73 mm，平均相对误差为0.07 mm。

3 结 语

在地面沉降监测中，D-InSAR监测值与水准监测数据总体变化趋势相似，但在数值上呈现出一定的差别。在靠近沉降盆地中心区域，D-InSAR监测值与水准监测数据差别较大；在靠近沉降盆地边缘区域，D-InSAR监测值与水准监测数据差别较小。本文利用集合卡尔曼滤波同化D-InSAR值和水准监测数据，使同化后的数据比D-InSAR监测值有了很大改善，更加符合地面沉降地区的沉降变形规律，为预测和防范地面沉降提供更为丰富的数据支持。

参考文献：

[1] HU R L，YUE Z Q，WANG L C，et al.Review on Current Status and Challenging Issuse of Land Subsidence in China[J].Engineering Geology,2004,76(1):65-77.

[2] 刘国祥,张瑞,李陶,等.基于多卫星平台永久散射体雷达干涉提取三维地表形变速度场[J].地球物理学报,2012,55(8):2598-2610.

[3] 舒宁.雷达影像干涉测量原理[M].武汉:武汉大学出版社,2003.

[4] 路旭,匡绍君,贾有良.用InSAR做地面沉降监测的试验研究[J].大地测量与地球动力学,2002,22(4):66-70.

[5] ZHAO Chaoying,DING Xiaoli,ZHANG Qin,et al.Monitoring of Land Subsidence and Ground Fissures in Xi’an China 2005—2006:Mapped by SAR Interferometry[J].Environ Geol,2009,58(3):1533-1540.

[6] 刘国祥，丁晓利.沿海地区D-InSAR形变探测：精度与可应用性分析[J].测绘通报，2006(9)：9-13.

[7] 陈春，吴振森，孙树计，等.集合卡尔曼滤波在电离层短期预报中的应用[J].空间科学学报，2010(2)：148-153.

[8] EVENSEN G.Sequential Data Assimilation with a Non-linear Quasi-geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics[J].Journal of Geophysical Research Oceans,1994,99(C5)：10143-10162.

[9] HOUTEKAMER P L,MITCHELL H L.A Sequential Ensemble Kalman Filter for Atmospheric Data Assimilation[J].Monthly Weather Review,2001,129(1):123-137.

[10] GILLIJINS S,MENDOZA O B,CHANDRASEKAR J,et al.What Is the Ensemble Kalman Filter and How Well Does it Work?[J].American Control Conference,2006(6):4448-4453.

[11] 崔波，张家树，杨宇.基于集合卡尔曼滤波的非线性目标跟踪算法[J].计算机仿真，2013,30(4)：317-321.

[12] 董亚宁.基于集合卡尔曼滤波全球臭氧卫星观测资料同化试验研究[D].南京：南京信息工程大学，2016.

[13] 惠雪峰.基于集合卡尔曼滤波的森林资源动态预测[D].南京：南京林业大学，2012.

[14] 米丽倩，查剑锋，王新.老采空区残余沉降的集合卡尔曼滤波预测[J].金属矿山，2012(8)：138-141.

[15] 李喜佳，肖志强，王锦地，等.双集合卡尔曼滤波估算时间序列LAI[J].遥感学报，2014，18(1)：27-44.