材料高压相变的理论模拟研究进展

瞿 洁，陈丽敏，李 俊，季培成，谢国治

南京邮电大学电子与光学工程学院微电子学院，江苏 南京 210003

近些年来，材料的计算机模拟设计技术日益受到大众的重视，是由于固体物理、量子化学、统计力学、计算数学等相关学科在理论基础和方法上的深入发展，为微观材料的结构设计提供了良好的理论基础。目前，研究物质在高压下的物理行为是计算材料设计的热点之一。高压可引起物质内部之间的相互作用，从而产生许多物质在常压下难以观察到的物理现象，是探寻具有新奇性质的新型材料的重要来源。

尽管近年来高压实验技术一直在发展，并且克服了许多难题，但仍然存在许多局限性。一方面，科学家研究的材料越来越复杂，现有的实验方法难以实现，并且高精度的原位测量技术也有待完善；另一方面，高昂的实验成本与代价让人望而却步。所以，对材料在高压条件下进行模拟计算方面的研究不仅是促进理论发展的原因，也是实验工作方面的迫切需求。

随着计算机的发明，在20世纪50年代，材料的计算机模拟设计技术这一思想被提了出来，而前苏联在此初期就进行了关于无机化合物的计算机预报以及合金设计等相关研究。这一技术使得多年前在数学计算和数据分析中仅靠人力无法解决的问题得到了解决。同时，科学的测量仪器的发展促进了定量测量水平的提高，为理论模拟设计提供了实验数据的支持。由于通过实验测量来研究高压下晶体的微观结构和性质仍然是一项具有挑战性的任务。因此，理论模拟是在原子层面了解固体材料性质的有效方法，它既是对实验工作不足的补充，也是高压下检测晶体性能的重要的替代方法。近年来，已经报道过很多基于密度泛函理论的固体材料结构和性质的高压研究［1-2］。

关于材料高压相变的研究对揭示材料的原子排列、电子结构等有重要的科学意义，在化学、生物科学及地球科学等方面也有广阔的应用前景。本文则是针对近些年理论模拟计算在材料高压相变中的重要作用，介绍了它的理论基础和计算方法，及其在材料高压相变方面的研究发现。

1 高压相变的理论基础

高压物理学是指以研究物质在高压条件下物理行为变化为目的的一门学科。高压物理学的应用领域涉及很广，其中在凝聚态物理方面主要研究的是极端条件下的物质的结构相变［3］、超导电性、超临界［4］等问题。而对于化学和材料科学，它的应用领域主要在超硬材料的合成及新型材料在工业上的应用［5］。

高压一般是指高于常压的压强条件。在高压的作用下，材料的体积会变小，原子（或者是分子）之间的距离会缩短，表现出和在常压下不同的性质，其中一个很新奇的物理现象就是结构相变，例如液态到固态的转变，非晶态到晶态的转变，半导体、绝缘体到金属的转变，金属到半导体或绝缘体的转变等。这些现象统称为高压相变。

2 高压相变的计算方法

通常，计算高压相变的方法有总能计算方法和分子动力学方法［6］。其中，总能计算方法在材料科学中的应用很广，在计算金属化相变、反金属化相变，以及半导体、简单分子等一些原子个数较少的分子的相变有很好的表现；分子动力学方法也有广泛的应用，特别是针对从固体到液体的相变计算，已经成为重要的科学研究的方法之一。

2.1 总能计算方法

在总能计算方法中，一般采用密度泛函理论或者Hartree-Fock（HF）理论对材料的电子结构、晶体性质等进行理论模拟。其计算相变的基本原理是：首先计算出一系列总能结构的能量-体积曲线，然后从中得到焓-压强曲线，因为在某一确定压强下，焓值越低就代表了系统热力学稳定性越高，所以在相同压强条件下，焓值最小的结构是最稳定的结构。而在前后两个相的焓值相等时，发生了结构相变。以BeO的相变为例，原鹏飞等［7］采用第一性原理方法计算了BeO在零温时的静态相变。相变的计算结果表明，在122 GPa左右的压力下BeO会从纤锌矿（B4）结构转变为氯化钠（B1）结构。图1给出了总能计算过程中BeO三种结构下的焓与压强的关系。从图1（a）中可以看到在120 GPa左右，B4和B1分别为最稳定结构；从图1（b）中可以看出在120 GPa左右，B4和B1这两个相的焓值相等，也就是说在这一位置，BeO发生了相变。

图1 三种结构的焓（H）与压强（p）的关系（a）H-p曲线，（b）ΔH-p曲线，以B4结构的焓作为基准［7］Fig.1 Relationship between enthalpy（H）and pressure（p）of three structures（a）H-p curves；（b）ΔH-p curves are based on the enthalpy of the B4 structure［7］

总能计算方法具有耗时短、计算简单、精度较高的优点。同时也存在一些缺点：计算的结构数目的受限；总能计算中的温度是0℃，与实验中的温度为室温存在差异；总能计算不能研究相变的动态过程。

2.2 分子动力学方法

分子动力学是一套分子模拟方法，该方法主要依靠牛顿力学来模拟分子体系的运动规律，并且在由分子体系的不同状态所构成的系综中抽取样本，从而计算体系的构型积分，并以构型积分的结果作为基础来进一步计算体系的热力学量和一些宏观性质。

分子动力学方法有4种系综，在高压相变方面应用的是等温等压系综：即系统的原子数、压力和温度均保持不变。其计算相变的基本原理是：在设定的压强和温度下，通过一定的时间后，材料会处在其最稳定的结构状态。首先计算出对应压强范围内的结果，然后画出体积对压强的曲线，如果体积在某一压强下发生了突变，结构就发生了相变。Focher等［8-9］采用第一性原理分子动力学的方法计算了Si的相变，结果发现Si从菱形（D）相到简单六角形（sh）相的相变压强在30 GPa左右。图2给出了分子动力学过程中的体积对压强的曲线，从图2中可以观察到在30 GPa左右，Si的体积发生了明显的突变，即发生了相变。

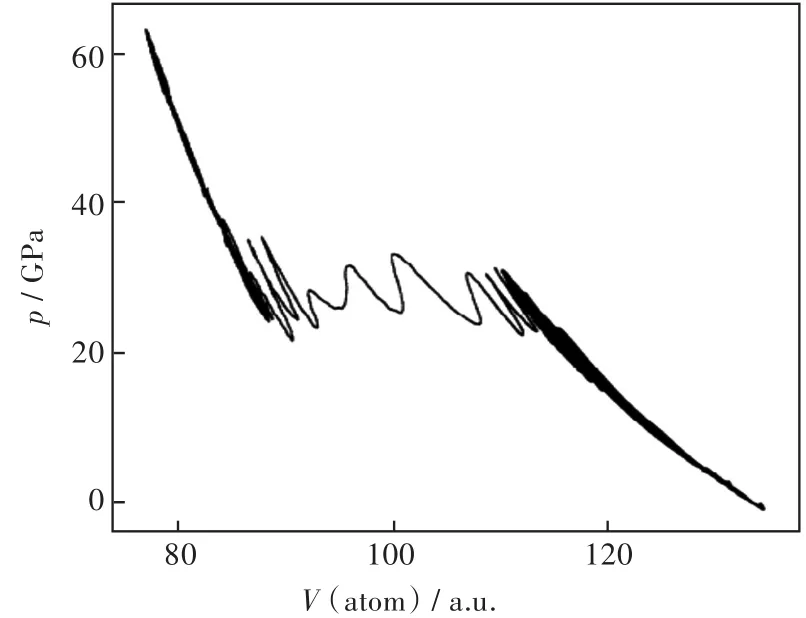
图2 在300 K的压缩过程中Si的压力与体积图［9］Fig.2 Pressure vs volume diagram of Si during the compression procedure at 300 K［9］

与总能计算方法相比，分子动力学方法具有动力学的模拟过程与实际相变过程一样、不需要预测相变以后的结构、可以计算相变的动态过程等优点。同时也具有计算时间较长、难以确定相变后的结构、难以判断相变发生的位置和精度不高的缺点。

3 高压相变的理论研究

当实验方面的研究方法不能满足科学研究工作的需求时，采用理论模拟计算却可以发现实验尚无法获得或很难获得的重要现象。虽然计算机模拟并不能完全取代实验，但可以用来指导实验以及验证某些理论假设，从而促进理论和实验的发展。特别是材料高压相变的过程中有许多与原子有关的微观变化，从而发生很多奇异的物理现象，例如金属化相变和反金属化相变、超导特性、硬度的提高、体积的压缩变化、磁性相变等。这些现象无法在实验中获取，但在计算机模拟中可以方便地得到。

3.1 金属化相变和反金属化相变

在压力的作用下，一些半导体或绝缘体的能带间隙会逐渐减小直到带隙闭合，发生向金属相的转变。同样对于金属而言，也可以在高压下实现向绝缘态的转变。

Yu等［10］运用了广义梯度近似（generalized gradient approximation，GGA）方法计算了单键立方相氮（cubic gauche nitrogen，cg-N）的态密度，预测了cg-N相氮从非金属到金属的相变发生在680 GPa的压力下。如图3所示，在0 GPa压力下，cg-N相氮是一个典型的绝缘体。随着压强的增加，价带和导带展宽，在700 GPa压强时，cg-N相氮已表现出典型的金属性。

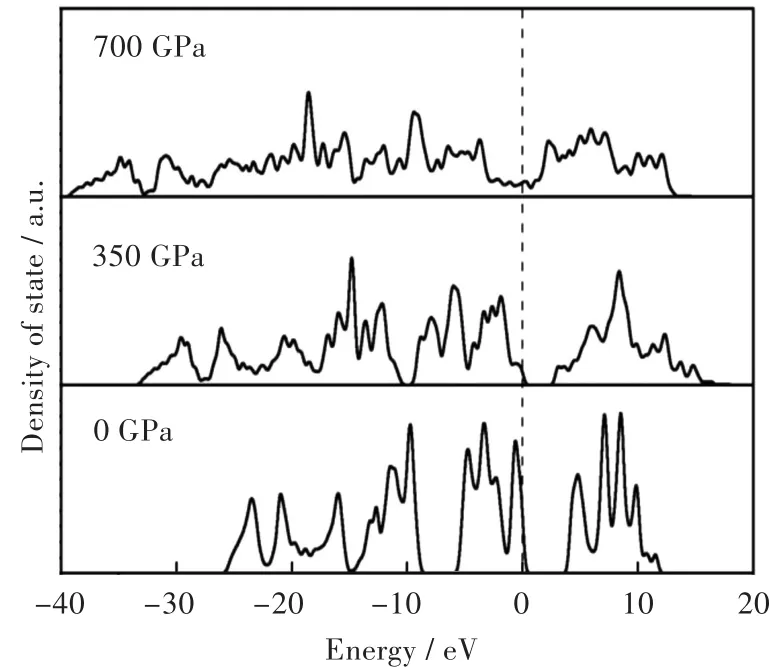
图3 cg-N在不同压力下的态密度。随着压力的增加，化合价和导带的增加导致带隙闭合和金属状态的形成［10］Fig.3 Density of states of cg-N under different pressures.The broadening of both the valence and conduction bands with increasing pressure leads to the band gap closure and the formation of metallic states［10］

周平等［11］采用第一性原理研究硫化镉，发现当压强大于2.18 GPa时，带隙消失，发生了从六方纤锌矿型（WZ）相向岩盐矿型（RS）相的金属化相变。吕梦雅等［12］使用第一性原理的GGA方法，结果发现实际的SiC相变过程在几何结构的转变的同时伴随着半导体-金属的电子转变。Chen等［13］采用了周期性密度泛函理论的方法，结果表明晶体α-DDCD在90 GPa下经历从半导体到金属的相变，并在110 GPa～170 GPa的压力范围内，发生了4次金属和半导体之间的重复变换。可见，高压引起的带隙减小可能会导致物质发生金属化相变。

3.2 超导现象

近年来，研究表明［14-17］压力可以通过调节电声子之间的作用和超导温度影响超导性，另外，压力还可以促使非超导体转变为超导体。

Yu等［14］通过基于密度泛函理论的第一性原理计算方法对CaLi2的高压结构进行了研究，通过电声相互作用强度的计算，发现高压下CaLi2的C2/c和P21/c结构转变为超导体。从图4可以看出，低频部分的谱函数对电声相互作用强度有着最大的贡献，而且电声相互作用的变化与低频部分的谱函数的变化有着明显的联系。

图4 （a）C2/c结构和（b）P21/c结构的谱函数α2F(ω )ω 。插图是电声耦合积分 λ(ω ) ［14］Fig.4 Spectral function α2F(ω )ωat selected pressures for（a）C2/cand（b） P21/cphases，respectively.The electron-phonon coupling integralλ(ω ) is plotted in the inset［14］

靳锡联等［18］采用基于第一性原理的方法，发现在高压下原子相的碘具有超导电性。董旭等［19］采用第一性原理计算，发现Bi的体心立方晶格（body centered cubic，bcc）结构和oC4结构的超导转变温度随压强的升高呈现降低的趋势。Otani等［20］采用了第一原理的方法，计算出Se的bcc型结构的超导转变温度Tc随压力的降低而显着增加。因此，高压下电声子的相互作用对超导性变化有一定的影响。

3.3 超硬性

材料的硬度主要是由晶体内原子间的成键决定的，由软化学键到硬化学键的变化导致了材料硬度的改变。另外，在较高的压力下，由于某些材料的不可压缩性使得其分子晶体的价电子密度变得很高，从而提高了材料的硬度。

Li等［21］利用第一性原理计算结合结构预测方法发现OsN是一种高硬度材料。研究表明Pmn21和Cmc21结构中的强共价键是其具有高硬度的根源，其中Pmn21结构中有强共价性的Os-N键，Cmc21结构中有强Os-N、N-N共价键。陈中钧等［22］采用基于密度泛函理论基础上的第一性原理赝势平面波方法，发现MgS的CsCl型结构抗压能力较强，随着压强增加，体弹模量逐渐增强，说明其结构在高压下具有较高的硬度和熔点。Wang等［23］采用了第一原理计算的方法，结果表明FeB-RhB的硬度达到了25 GPa，是一种硬质材料。丁迎春等［24］基于密度泛函理论的研究发现高压的尖晶石结构的BeP2N4是一种耐压缩材料，其硬度非常高，大约为43 GPa。所以，方向性强的共价键及较强的抗压缩性是形成高硬度材料的必要条件。

3.4 体积压缩

由弱的范德瓦尔斯作用相结合的分子晶体是一种较软的物质，在压力的作用下很容易被压缩，除了分子间距变小以外，分子本身也会发生形变，甚至塌陷。明星等［25］采用基于密度泛函理论的平面波赝势法和自旋极化的GGA研究FeCO3，计算结果表明在40 GPa～50 GPa压力范围内，单胞体积坍塌了10.5%，如图5所示。体积坍塌的原因：一是在压力范围内发生了高自旋（HS）态到低自旋（LS）态的自旋相变，而HS态的Fe2+离子比LS态的半径大；二是费米面附近的离子的能带变窄，说明离子的电子局域化程度更强，导致晶胞坍塌。

图5 FeCO3单胞体积随压力的变化情况图（插图显示40 GPa～50 GPa压力范围内体积坍塌了10.5%）［25］Fig.5 Change of FeCO3cell volume with pressure（The inset shows that cell volume collapses by 10.5%at pressures of 40 GPa-50 GPa）

王斌等［26］基于密度泛函理论的第一性原理平面波赝势方法，计算得到了零温时，TiC晶体随着压强增大被压缩，但是抗变形能力和延展性增强。Chen等［27］通过密度泛函理论的计算，发现结晶L-丝氨酸-L-抗坏血酸（SAA）的单位体积随着压力的增加而降低，而在300 GPa下的总压缩达到65.4%。周平等［11］采用第一性原理的计算发现，硫化镉WZ→RS的相变同时伴随着20%的体积塌缩。可见，体积的压缩总是伴随着几何结构参数和结构相变的变化。

3.5 磁性相变

Zhou等［28-31］曾指出RCrO3中存在的3 d轨道交换劈裂和t-e轨道杂化导致了弱铁磁性的产生。另外，费米能级附近的态密度下降、能带展宽等原因也可能引起磁性相变。

Mohammed 等［32］采用基于密度泛函理论的GGA和GGA+U的方法计算了Fe和Co。结果发现：GGA和GGA+U计算表明Fe分别在12 GPa和115 GPa由铁磁性（ferromagnetism，FM）的bcc结构转变为非磁性（non-magnetic，NM）的密堆六方结构（hexagonal closed-packed，hcp）结构。GGA计算发现Co在压力为107 GPa左右从FM的hcp转变到NM 的面心立方晶格（face-centered cubic，fcc）结构。如图6所示，Fe，Co在费米能级附近的态密度随压力的增加而减小。依据Stoner标准，可以得出由压力引起的费米能级附近的态密度下降导致了磁性抑制。

图6 计算总态密度：（a）GGA，（b）GGA+UFig.6 Calculated total density of state：（a）GGA，（b）GGA+U

蔺何等［33］通过第一性原理的方法，结果表明CrN在132 GPa发生了由反铁磁岩盐结构到NM的Pnma结构的相变。在压力的作用下，能带展宽使部分电子发生自旋翻转，从而导致Cr离子磁矩减小。

Qian等［34］基于密度泛函理论的第一性原理的计算表明，在Cr-O-Cr晶格中的交换劈裂和t-e轨道杂化的产生和消失导致了SmCrO3弱铁磁性的产生。

4 结 语

介绍了理论计算方法在材料高压模拟中的一些研究进展，以及目前计算高压相变的2种常用方法，重点总结归纳了物质在高压下的相变机制以及物理性能的变化现象。总而言之，材料的高压相变模拟方法具有广阔的应用前景，目前还处于发展阶段，基础理论和实际应用上的困难尚未得到完全解决，仍有待众多领域科学家们的合作来共同解决。

［1］RAMESH BABU K，BHEEMA LINGAM C，TEWARI S P，et al.High-pressure study of lithium azide from density-functional calculations［J］.Journal of Physical Chemistry A，2011，115（17）：4521-4529.

［2］TAKAHASHI M,KAWAZOE Y,ISHIKAWA Y,et al.Interpretation of temperature-dependent low frequency vibrational spectrum of soild-state benzoic acid dimer［J］.Chemical Physics Letters，2009，479（4/5/6）：211-217.

［3］杨向东，张宏，胡栋，等.高温高压下碳的状态方程及相变理论研究［J］. 高压物理学报，1997，11（4）：250-253.

［4］JENNINGS L D，SWENSON C A.Effects of pressure on the superconducting transition temperatures of Sn，In，Ta，TI，and Hg［J］.PhysicalReview，1958，112（1）：31-43.

［5］KNITTLE E，WENTZCOVITCH R M，JEANLOZ R，et al.Experimental and theoretical equation of state of cubic boron nitride［J］.Nature，1989，337（6205）：349-352.

［6］原鹏飞.第一性原理方法计算几种材料高压下的相变和弹性性质［D］.合肥：中国科学技术大学，2007.

［7］原鹏飞，祝文军，徐济安，等.BeO高压相变和声子谱的第一性原理计算［J］. 物理学报，2010，59（12）：8755-8761.

［8］FOCHER P，CHIAROTTI G L，BERNASCONI M，et al.Structural phase-transformations via 1st-principles simulation［J］.EurophysicsLetters，1994，26（5）：345-351.

［9］BERNASCONI M，CHIAROTTI G L，FOCHER P，et al.First-principle-constantpressure moleculardynamics［J］.Journal of Physics&Chemistry of Solids，1995，56（3/4）：501-505.

［10］YU H L，YANG G W，YAN X H，et al.First-principles calculationsofthe single-bonded cubic phase of nitrogen［J］.Physical Review B，2006，73（1）：012101（1）-012101（4）.

［11］周平，王新强，周木，等.第一性原理研究硫化镉高压相变及其电子结构与弹性性质［J］.物理学报，2013，62（8）：87104（1）-87104（9）.

［12］吕梦雅，陈洲文，李立新，等.3C-SiC高压相变的理论研究［J］. 物理学报，2006，55（7）：3576-3580.

［13］CHEN L M，FANG H N，XIE Q Y.DFT study of the structural transformations and absorption properties of crystalline 2，6-dimethyl-4-（diphenylmethylene）-2，5-cyclohexadienone under hydrostatic compression［J］.International Journal of Modern Physics C，2016，28（2）：1750027（1）-1750027（18）.

［14］XIE Y，OGANOV A R，MA Y M.Novel high pressure structures and superconductivity of CaLi2［J］.Physical Review Letters，2010，104（17）：177005（1）-177005（4）.

［15］CALAMIOTOU M，GANTIS A，LAMPAKIS D，et al.Pressure-induced phase separation in the Y123 superconductor［J］.Europhysics Letters，2009，85（2）：26004（1）-26004（4）.

［16］胡保付，王会新，李明，等.金属间化合物MgB2电子结构与超导电性的研究［J］. 核技术，2009，32（10）：764-768.

［17］NAKAYAMA A，ONDA Y，YAMADA S.Collapse of CuO double chains and suppression of superconductivity in high-pressure phase of YBa2Cu4O8［J］.Journal of the Physical Society of Japan，2014，83（9）：238-241.

［18］靳锡联，崔田.高压下典型小分子晶体的结构和行为［J］. 高压物理学报，2013，27（2）：188-198.

［19］董旭，范长增.高压下Bi的第一性原理研究［J］.燕山大学学报，2014，38（6）：497-502.

［20］OTANI M，SUZUKI N.Structural and superconducting transition in selenium at high pressure［J］.Physical Review B，2001，63（10）：385-392.

［21］LI Y W，MA Y M.Crystal structure and physical properties of OsN：First-principle calculations［J］.SolidStateCommunications，2010，150（15/16）：759-762.

［22］陈中钧.高压下MgS的弹性性质、电子结构和光学性质的第一性原理研究［J］.物理学报，2012，61（17）：445-449.

［23］WANG Q Q，ZHAO Z S，XU L S，etal.Novel high-pressure phase of RhB：first-principles calculations［J］.Journal of Physical Chemistry C，2011，115（40）：19910-19915.

［24］丁迎春，刘海军，蒋孟衡，等.高压下BeP2N4结构相变和电子结构的第一性原理计算［J］.高压物理学报，2012，26（6）：674-680.

［25］明星，王小兰，杜菲，等.菱铁矿FeCO3高压相变与性质的第一性原理研究［J］. 物理学报，2012，61（9）：097102（1）-097102（6）.

［26］王斌，刘颖，叶金文.高压下TiC的弹性、电子结构及热力学性质的第一性原理计算［J］.物理学报，2012，61（18）：186501（1）-186501（11）.

［27］CHEN L，LIU C，FANG H，et al.Periodic density functional theory study of the high-pressure behavior of crystalline l-serine-l-ascorbic acid ［J］. Journal of Molecular Modeling，2016，22（1）：1-11.

［28］CHENG J G，SUI Y，ZHOU J S，et al.Transition from orbital liquid to jahn-teller insulator in orthorhombic perovskites RTiO3［J］.Physical Review Letters，2008，101（8）：087205（1）-087205（11）.

［29］ZHOU J S，GOODENOUGH J B，YAN J Q，et al.Superexchange interaction in orbitally fluctuating RVO3［J］.Physical Review Letters，2007，99（15）：156401（1）-156401（4）.

［30］YAN J Q，ZHOU J S，GOODENOUGH J B，et al.Orbitalfluctuationsand orbitalflipping in RVO3perovskites［J］.Physical Review Letters，2007，99（19）：197201（1）-197201（4）.

［31］LANDRON S，LEPETIT M B.Importance oft2g-eg，hybridization in transition metal oxides［J］.Physical Review B，2008，77（12）：125106（1）-125106（8）.

［32］MOHAMMED Y S，YAN Y，WANG H X，et al.Stability of rerromagnetism in Fe，Co，and Ni metals under high pressure with GGA and GGA+U［J］.Journal of Magnetism and Magnetic Materials，2010，322（6）：653-657.

［33］LIN H，ZENG Z.Structural，electronic，and magnetic properties of CrN under high pressure［J］.Chinese Physics B，2011，20（7）：077102（1）-077102（6）.

［34］QIAN X L，CHEN L，CAO S X，et al.A study of the spin reorientation witht-eorbital hybridization in SmCrO3［J］.Solid State Communications，2014，195：21-25.