钻井地质力学参数空间建模技术

杨同玉，吴 超，吴继伟

(1.中国石化华北分公司，河南 郑州 450006；2.中国石化石油工程技术研究院，北京 100101；3.中国石油新疆油田分公司，新疆 克拉玛依 834000)

0 引 言

钻井地质力学参数通常包括岩石变形参数、抗压强度、抗剪强度、抗拉强度、可钻性、构造应力、孔隙压力、坍塌压力、破裂压力等。精细描述钻井地质力学参数的分布规律将有助于全面认识钻井破岩能力和井身质量控制难点，为优化井身结构、井眼轨迹、钻头型号及机械水力参数、钻具组合、井控方案、钻井液性能等工艺措施提供依据，为实现安全、优质、高效、低成本钻井打下坚实基础[1]。

数学地质理论认为，地质参数在地下三维岩层空间中的分布具有统计相关性与随机性的特征[2-3]。基于地球物理信息可建立三维地层空间的钻井地质力学参数模型，从而掌握区域力学特征，以合理优化目标井(尤其是定向井、水平井)钻井工程技术方案。近年来，国内外学者基于非线性优化理论提出了多种钻井地质力学参数预测方法[4-10]，但多针对井壁围岩，将其推广至三维地层空间存在难度。有学者尝试将地震层析与储层建模算法用于力学参数三维建模，但现场应用表明，其计算精度和分辨率均存在一定限制[11-14]。因此，有必要研发一套精度高、适用面广的钻井地质力学参数空间建模技术，使其更加有利于指导钻井提速提效工作。为此，提出一种基于地震属性的钻井地质力学参数空间建模方法。针对目标工区，利用完钻井资料建立层速度与地震属性之间的分层神经网络模型，利用其预测三维地层空间的层速度及各类钻井地质力学参数，进一步确定区域地层力学分布特性，并将其用于钻井工程优化设计。

1 理论基础

按照地球物理原理，地下界面的反射系数和地震子波经褶积运算可得到叠后地震记录数据，即：

(1)

式中：D(i)、R(i)、W(i)分别为地震记录、反射系数和地震子波；i为地层深度点序号；*表示褶积运算。

根据勘探地震学理论，反射系数的数值取决于地震波反射界面两侧地层的波速和密度：

(2)

式中：ρ为地层密度，g/cm3；vp为纵波速度，m/s。

岩石物理实验研究表明，岩石的纵波速度和密度之间存在较好的经验关系：

ρ=C0vpC1

(3)

式中：C0、C1为经验参数。

综合分析式(1)、(2)、(3)可知，叠后地震记录和纵波速度之间存在直接的定量关系。由于纵波速度是计算各类钻井地质力学参数的最重要、最基础的数据，因此，可考虑使用地震记录反演求取地层纵波速度，从而进一步预测地层空间三维区域内的各类力学参数。

受复杂地层条件影响，地震记录与波速之间存在非线性映射关系，对于同一工区的相同地质层段，所体现出的上述映射关系是相近的，因此，可以借鉴人工智能方法，根据完钻井数据信息，利用神经网络算法识别这类映射关系，并将其推广至工区中的未钻探空间。

2 地震层速度的预测

地震属性是从地震记录中通过特定数学方法提取的多种参数，可从多角度反映地层的构造、岩性、物性以及流体成分等特征，相比于原始地震记录，其更适宜用来建立层速度与地震反射信息之间的非线性映射关系[15-18]。此次研究提取并使用的地震属性为：①反映界面反射特征的振幅属性，包括均方根振幅、平均绝对振幅、相邻时窗振幅比等；②描述地震信号瞬时变化规律的瞬时属性，包括瞬时振幅、瞬时相位、瞬时频率等；③体现一定时窗内地层岩性、构造与物性变化的傅立叶谱属性，包括振幅谱主频、振幅谱极大值、平均中心频率等；④反映地震随机特征的功率谱属性，包括加权平均频率、功率谱极大频率等。

人工智能领域已研发了多种神经网络方法，其中，小波神经网络模式识别速度快、容错能力强[19-20]，因此，此次研究中运用小波神经网络进行地震层速度预测，具体步骤如下。

(1) 设定小波函数，其神经网络输出yl′为：

(4)

式中：ak、bk为小波函数因子；ωk1、ωkj2为神经网络权值(上标表示权值类别)；xlj表示地震属性；l=1,2,…，m,m为学习样本对的数量；j=1,2,…，n,n为所使用地震属性的种类数；k=1,2,…，t,t为基函数个数。

(2) 将ak、bk、ωk1、ωkj2随机设定初始值。对于目标工区内钻遇的各套地层，将其地震属性及相应的测井声波速度作为学习样本对，导入神经网络进行映射关系识别。

(5)

式中：μ为网络参数；p为迭代次数；γ为学习率；ξ为动量项。

按上述计算步骤迭代计算，直至误差满足要求，即可完成网络模式识别。在此基础上，将工区未钻探空间内的地震属性输入网络，得到各地震道上的层速度，从而建立工区三维地震层速度数据体。

3 钻井地质力学参数空间建模方法

在利用地震属性预测得到地下空间的三维地层纵波速度数据的基础上，可运用岩石力学方法进一步预测各类钻井地质力学参数[21-23]。对于鄂尔多斯南部探区，通过实测数据统计拟合，建立起各类岩石物理及力学参数计算模型。利用纵波速度预测得到横波速度、密度、孔隙度、泥质含量等岩石物理参数，进而预测弹性模量、泊松比、黏聚力、内摩擦角、抗拉强度、上覆压力、水平地应力等力学参数。通过统计拟合建立了地层孔隙压力模型为：

(6)

式中：pe为垂直应力，MPa；pp为孔隙压力，MPa；Vsh为泥质含量；φ为孔隙度；σv为上覆压力，MPa；w1、w2、w3、w4、w5为经验系数，对于鄂南工区，w1=4.71,w2=-4.086,w3=-0.046 3,w4=0.018 8,w5=-0.021 5 。

井壁稳定分析是钻井地质力学分析的重点，通常根据剪切破坏准则和拉伸破坏准则建立井壁失稳力学模型，最终可得到坍塌压力和破裂压力的计算公式：

(7)

pf=3σh-σH-αpp+St

(8)

式中：pc为坍塌压力，MPa；pf为破裂压力，MPa；σH和σh分别为最大和最小水平地应力，MPa；C为岩石的黏聚力，MPa；α为有效应力系数；K=ctan(45-φ/2) ，φ为内摩擦角，°；η为应力修正系数；St为抗拉强度，MPa。

岩石可钻性是表征地层抗钻能力的重要参数，其与层速度关系密切。根据实验室测试数据分析，建立了适用于目标工区的可钻性级值计算模型：

(9)

式中：Kdy1和Kdpdc分别为牙轮钻头和PDC钻头可钻性级值；k0、k1、k2、k3为由统计拟合得到的经验系数，对于鄂南工区，k0=0.000 36,k1=1.153 00,k2=0.000 257,k3=1.175 00 。

按照上述方法，可基于地震层速度导出各类钻井地质力学参数三维数据体，建立相应的空间数据模型。运用三维地质体描述软件，可对相关力学参数进行三维空间成像，并进行空间剖面和切片分析，以获得各类力学参数的空间分布特征，为钻井优化设计提供依据。

4 现场应用

镇泾探区位于鄂尔多斯盆地西南缘，区内钻井以水平井为主，由浅至深依次钻遇第四系、罗汉洞组、环河组、华池组、洛河-宜君组、安定组、直罗组、延安组及延长组，完钻井深为3 000 m左右。前期6口完钻井由于对地层可钻性认识不全面，导致钻头选型针对性差，破岩效果不理想，机械钻速有待提高。

将镇泾探区内东部井区待钻的YS101、YS301、YS5、YS6、YS9等5口井作为试验井，利用上述钻井地质力学参数空间建模方法，分层段依次由浅至深建立了该地区的层速度、弹性模量、抗压强度、可钻性级值、地应力、孔隙压力、坍塌压力、破裂压力等多种参数的空间数据体。限于篇幅，只显示目标井区重点层段的可钻性级值及孔隙压力、坍塌压力、破裂压力(简称地层三压力)空间数据体三维成像效果(图1—4)。由图1—4可知，力学参数建模结果具有较高的分辨率。从上述数据体中提取5口试验井的数据剖面(以YS5井为例，图5)，进行试验井地层力学参数特征分析，在此基础上对其进行必要的钻井工艺措施优化，在试验井完钻后收集了相关测井、钻井数据以验证建模预测效果。由图5可知，预测的坍塌压力、钻井液密度与井径扩大率等曲线的匹配程度较高。将试验井力学参数预测值与实测结果进行了对比(表1)，各测试点的预测误差均低于10%。以上均证明钻井地质力学参数建模技术的可靠性。

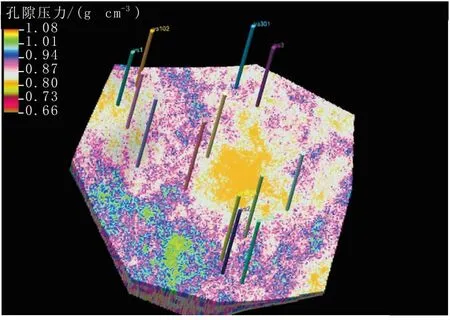
图1镇泾东部井区洛河-宜君组孔隙压力数据体成像效果

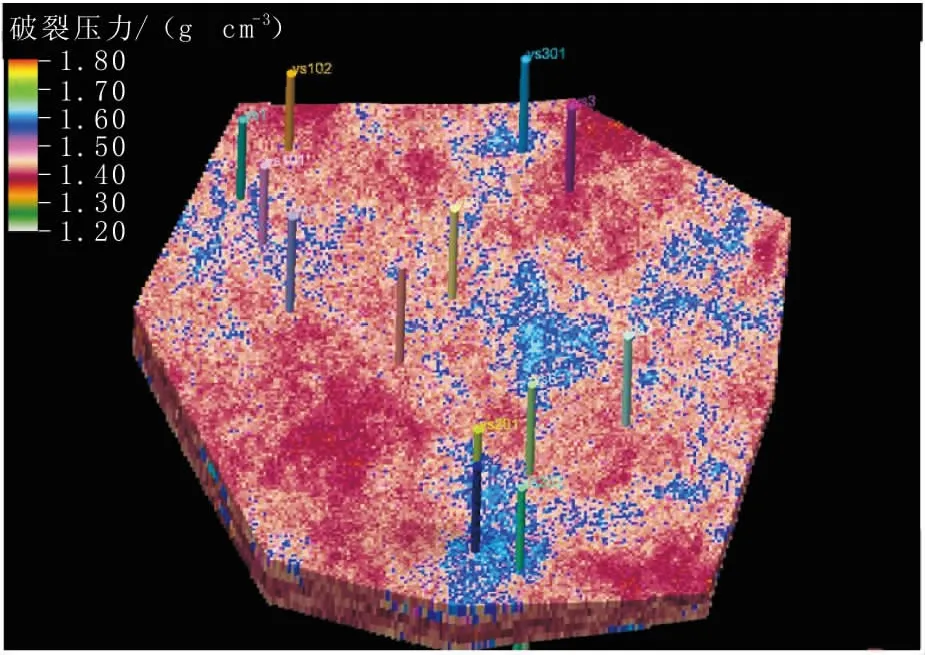
图3镇泾东部井区环河组破裂压力数据体成像效果

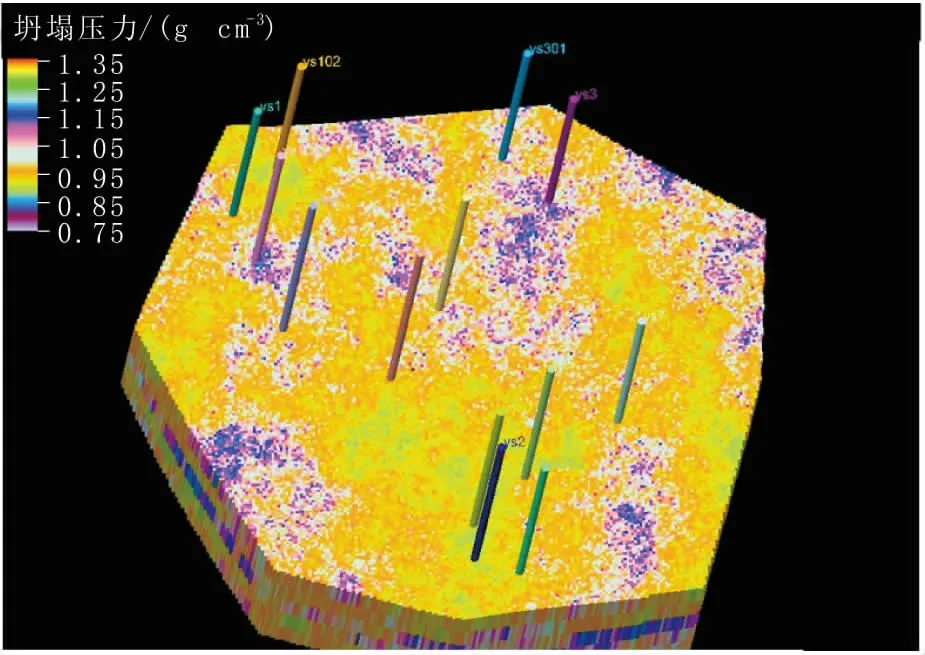
图2镇泾东部井区延安组坍塌压力数据体成像效果

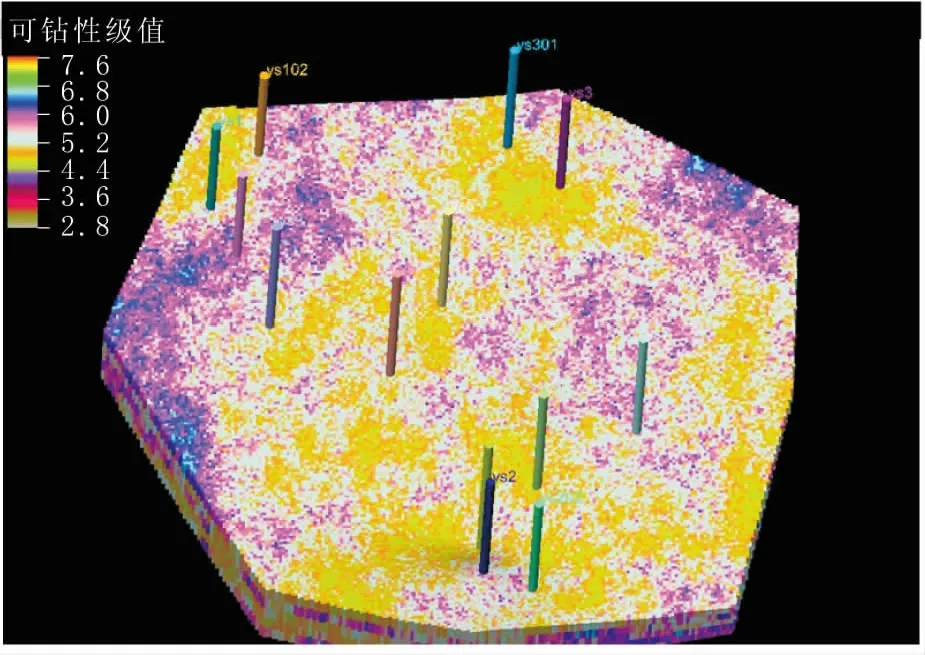
图4镇泾东部井区安定组可钻性级值数据体成像效果

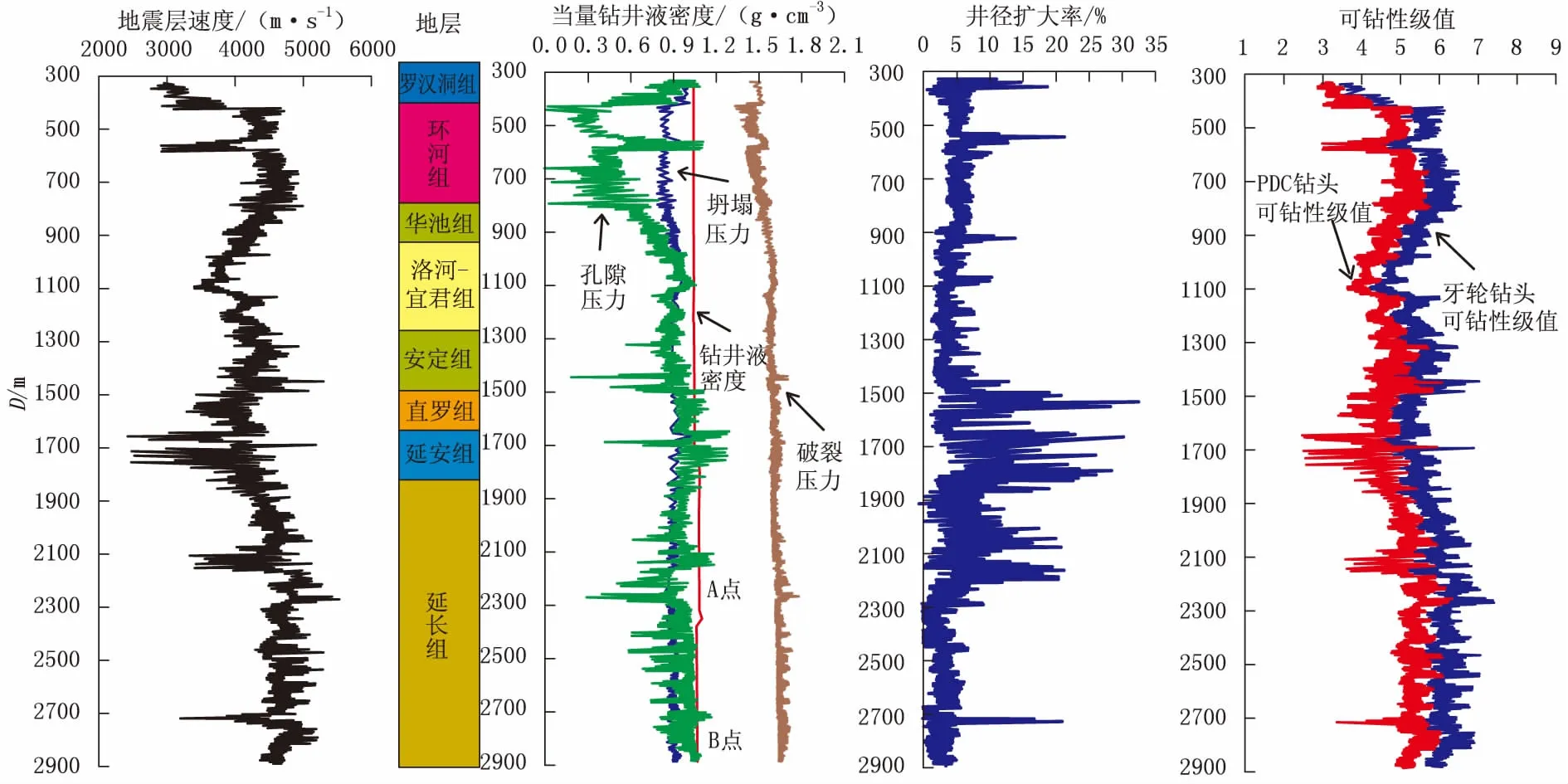
图5从空间数据体中提取的YS5井的层速度与力学参数预测剖面

通过分析镇泾东部井区地层三压力空间建模结果，确定了该区三压力纵向和横向分布特征，在重点考虑环河组、延安组、延长组等压力分布异常地层的基础上，结合工程需求，提出了目标井区水平井井身结构优化方案。该地区前期水平井采用三开井身结构，针对提速提效需要，提出了2种井身结构优化方案。一是对于该区井深超过2 800 m的水平井，仍然推荐采用三开井身结构，为提高斜井段钻井速度及控制阻卡，建议二开采用复合井眼(表2)。对于井深低于2 800 m的水平井，充分考虑提高钻速、降低成本、提高固井质量的需要，推荐二开井身结构(表3)。基于井身结构优化方案，进一步优化了目标井区的钻井液密度(表4)。

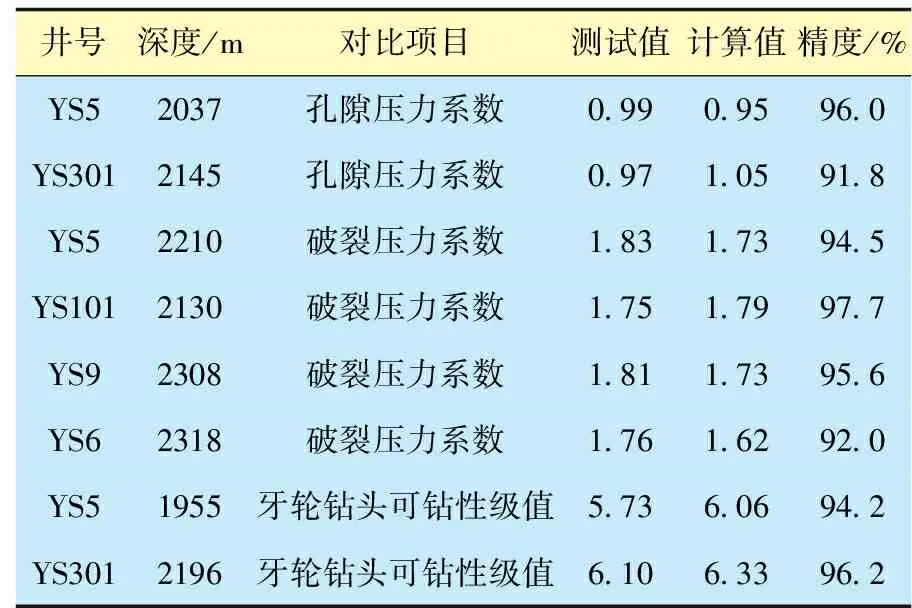
表1 镇泾东部井区试验井测试点上的实测值和预测值对比

表2 镇泾东部井区水平井三开井身结构优化方案

表3 镇泾东部井区水平井二开井身结构优化方案

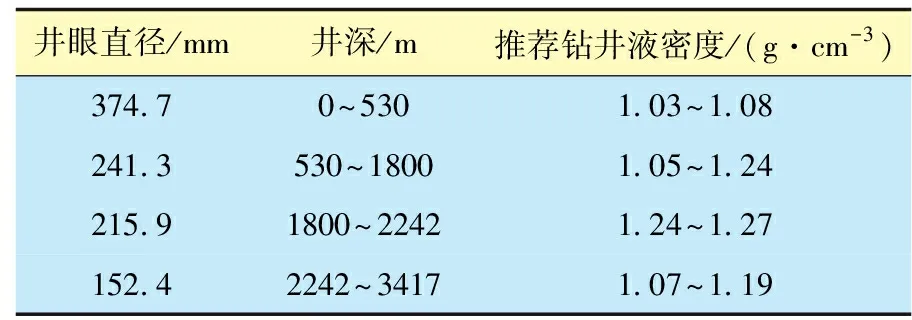
表4 镇泾东部井区水平井钻井液密度优化方案

通过分析镇泾东部井区地层可钻性空间建模结果，确定了该区岩石可钻性纵向和横向分布特征，结合实际施工条件，对该区的钻头型号及相关工程参数进行了优化(表5)。

表5 镇泾东部井区水平井钻头及相关工程参数优化方案

5口试验井均采用了上述工程优化方案。实钻表明，5口井平均机械钻速为10.80 m/h，对比该井区前期完钻井7.49 m/h的平均钻速，提高了44.19%，提速效果明显。其中，YS9井采用推荐的二开井身结构，钻井周期为23.67 d，较之前期完钻井缩短了51.70%，节约成本近210×104元。试验井的平均井径扩大率和漏失量相比前期完钻井均减少40%以上。上述现场实际情况均表明，文中提出的钻井地质力学参数建模方法可有效满足工程优化的需求。

5 结 论

(1) 地层声波传播速度是定量计算各类岩石物理与力学参数的基础数据，基于地震资料预测的速度信息可用于进行钻井地质力学参数三维空间建模。

(2) 地震属性和声波速度之间存在映射关系，据此可运用智能算法由地震信息反演得到层速度，进而建立钻井地质力学参数的空间三维数据模型。

(3) 现场应用情况表明，文中提出的钻井地质力学参数空间建模方法能达到较高的参数预测精度和成像分辨率，以此为基础进行的钻井工艺措施优化具有较强的针对性和适用性。

[1] 吴超，陈小锋，张东清，等.岩石力学特征分析技术及其在元坝气田的应用[J].测井技术，2015，39(2)：247-252.

[2] 吴胜和.储层表征与建模[M].北京：石油工业出版社，2010：290-355.

[3] 乐友喜，曾勉，问雪，等.利用序贯高斯随机模拟分析构造图的不确定性[J].石油地球物理勘探，2017，52(2)：333-339.

[4] 吴超，臧艳彬，张东清，等.定向井随钻井壁稳定预测方法及其应用[J].石油学报，2015，36(10)：1290-1298.

[5] WU C，CHEN M，JIN Y.A prediction method of borehole stability based on seismic attribute technology[J]. Journal of Petroleum Science and Engineering，2009，65(3/4)：208-216.

[6] WU C，LIU J，ZHANG D，et al. A prediction of borehole stability while drilling preliminary prospecting wells based on seismic impedance[J].Petroleum Exploration and Development.2015，42(1)：390-395.

[7] 金衍，陈勉.利用地震记录钻前预测井壁稳定性研究[J].石油学报，2004，25(1)：89-92.

[8] 金衍，陈勉，杨小奇.利用层速度钻前预测安全泥浆密度窗口[J].岩石力学与工程学报，2004，23(14)： 2430-2433.

[9] WU C，CHEN M，JIN Y.Real-time prediction method of borehole stability[J].Petroleum Exploration and Development，2008，35(1)：80-84.

[10] 金衍，陈勉，张旭东.钻前井壁稳定预测方法的研究[J].石油学报，2001，22(3)：96-99.

[11] AZEDOVE L，NUNES R，CORREIA P，et al. Multidimensional scaling for the evaluation of a geostatistical seismic elastic inversion methodology[J].Geophysics，2014，79(1)：M1-M10.

[12] 吴超，刘建华，张东清，等.基于非线性反演的井壁稳定随钻预测方法[J].岩土工程学报，2015，37(10)： 1810-1817.

[13] BOSCH M，MUKERJI T，GONZALEZ E F.Seismic inversion for reservoir properties combining statistical rock physics and geostatistics：A review[J].Geophysics，2010，75(5)：A165-A176.

[14] ESMERSOY C，RAMIREZ A，TEEBENNY S.A new fully integrated method for seismic geohazard prediction ahead of the bit while drilling[J].Leading Edge，2013，32(10)：1222-1233.

[15] 卢宝坤，史謌.测井资料与地震属性关系研究综述[J].北京大学学报(自然科学版)，2005，41(1)：154-160.

[16] 张阳，邱隆伟，李际，等.基于模糊C均值地震属性聚类的沉积相分析[J].中国石油大学学报(自然科学版)， 2015，39(4)：53-61.

[17] NEVES F A，ZAHRANI M S，BREMKAMP S W，et al. Detection of potential fractures and small faults using seismic attributes[J]. Leading Edge，2004，23(9)：903-906.

[18] NATH S K，DEWANGAN P.Detection of seismic reflections from seismic attributes through fractal analysis[J]. Geophysical Prospecting，2002，50(3)：341-360.

[19] 彭琦，张茹，谢和平，等.基于AE时间序列的岩爆预测模型[J].岩土力学，2009，30(5)：1436-1440.

[20] 曹爱武，顾圣平，何露，等.基于小波神经网络的水库泥沙预测[J].江南大学学报(自然科学版)，2015，14(3)： 338-343.

[21] ZHANG J.Borehole stability analysis accounting for anisotropies in drilling to weak bedding planes[J].International Journal of Rock Mechanics and Mining Sciences，2013，60(3)：160-170.

[22] 卢运虎，陈勉，袁建波，等.各向异性地层中斜井井壁失稳机理[J].石油学报，2013，34(3)：563-568.

[23] 楼一珊，金业权.岩石力学与石油工程[M].北京：石油工业出版社，2006：99-137.