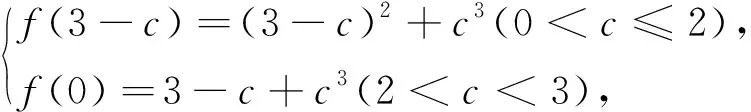退到基本的方程函数上，跳出困境解难题

贵州省毕节市梁才学校 (551700) 熊福州

多元函数t=G(x,y,z)(F(x,y,z)=0)中，人为定义域F(x,y,z)=0又叫约束条件，求这类函数最值问题，在高考和竞赛中比较常见，命题者多伴是从比较难想到的技巧转化为用均值不等式或柯西不等式解决设计的，解题者按命题者的思路解就中计了，陷入冥思苦想而不得解的困境，若能退到基本的方程函数上，则可跳出困境，解决问题.

例1 (2006年全国高考重庆卷文第12题)若a,b,c>0，且a2+2ab+2ac+4bc=12，则a+b+c的最小值是 .

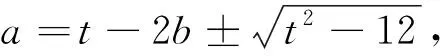
例2的参考解答很不易想到，为便于比较，先把参考解答过程详录于下.

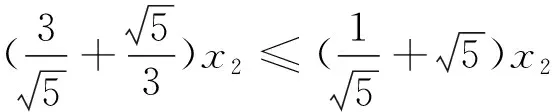
注：例2中，z(x2)是二次函数，z(x2)min和

z(x2)max可直接由二次函数在闭区间上求得，只是配方过程中的运算比较繁，故本文用略显简单些的导数法,解题过程为消元将三元函数化为二元函数，再认一元(主元，即自变量)定一元(次元，即参数)求最值，最后求次元(参数)为自变量的函数最值，凡是元不多(不超过3个)，次数不高(不超过3次)的函数求最值，当用已知不等式(如均值不等式，柯西不等式等)不易解决(因为很难想到怎样变形转化，即变形技巧很强)时，不妨退到用函数性质(单调性，极限)求函数的值域上，通过基本的换元，消元，认元逐步解决，运算虽然繁一点，但好想，且问题本质暴露无遗(如例2中取最小值的自变量不唯一，是两组，即x3=1,x2=x1=0，或x3=0,x2=1,x1=0时，zmin=1).

f(b)max=g(c)=