人为过失对高支模支架安全性的影响

2018-07-01

安徽工业大学学报（自然科学版） 2018年4期

(安徽工业大学建筑工程学院,安徽马鞍山243032)

随着我国城镇化建设的不断发展，高支模支架体系所借鉴的相关支架规范也日趋完善[1-2]。然而高支模支架事故仍频频发生。分析近年来多起高支模支架事故发现，人为过失是导致高支模支架事故的重要原因之一[3-5]。国内外一些学者对此进行了相关研究，如：谢楠等[6]通过对高支模支架中人为过失的调查,探讨了人为过失的发生规律，并对人为过失对高支模结构承载力的影响及多个人为过失因素同时出现时高支模支架的可靠度等进行了分析；宋方方[7]利用ANSYS软件对高支模支架承载力进行模拟分析，得到了人为过失影响下承载力的变化规律，并采用鱼刺图分析的方法，得出高支模事故主要来源于人为失误的结论；赵凯[8]对高支模板支架进行优化设计，利用有限元分析了在有、无人为过失两种情况下，高支模支架的可靠性；Stewart[9]利用可靠性分析(HRA)模型模拟人为过失对钢筋混凝土梁结构的影响，认为人为过失是导致结构不安全的重要原因。

本文依照人为过失因素对高支模支架安全体系影响权重大小，构建高支模支架人为过失层次结构体系，进而通过数值模拟，探讨人为过失对高支模支架安全性的影响。

1 人为过失结构层次体系的建立

人为过失指的是所有达不到有关规范、标准、规程要求的行为与结果[10]。通过对高支模支架事故的实地调研，结合当前相关高支模支架的研究成果[11-13]，目前主要存在4类人为过失问题：高支模支架的结构布置人为过失问题；高支模支架材料质量和几何参数人为过失问题；施工过程模板支架搭设安装人为过失问题；相关的监管与检查人为过失问题。本文选取16种常见人为过失，构建考虑人为过失影响的层次结构体系，如图1。

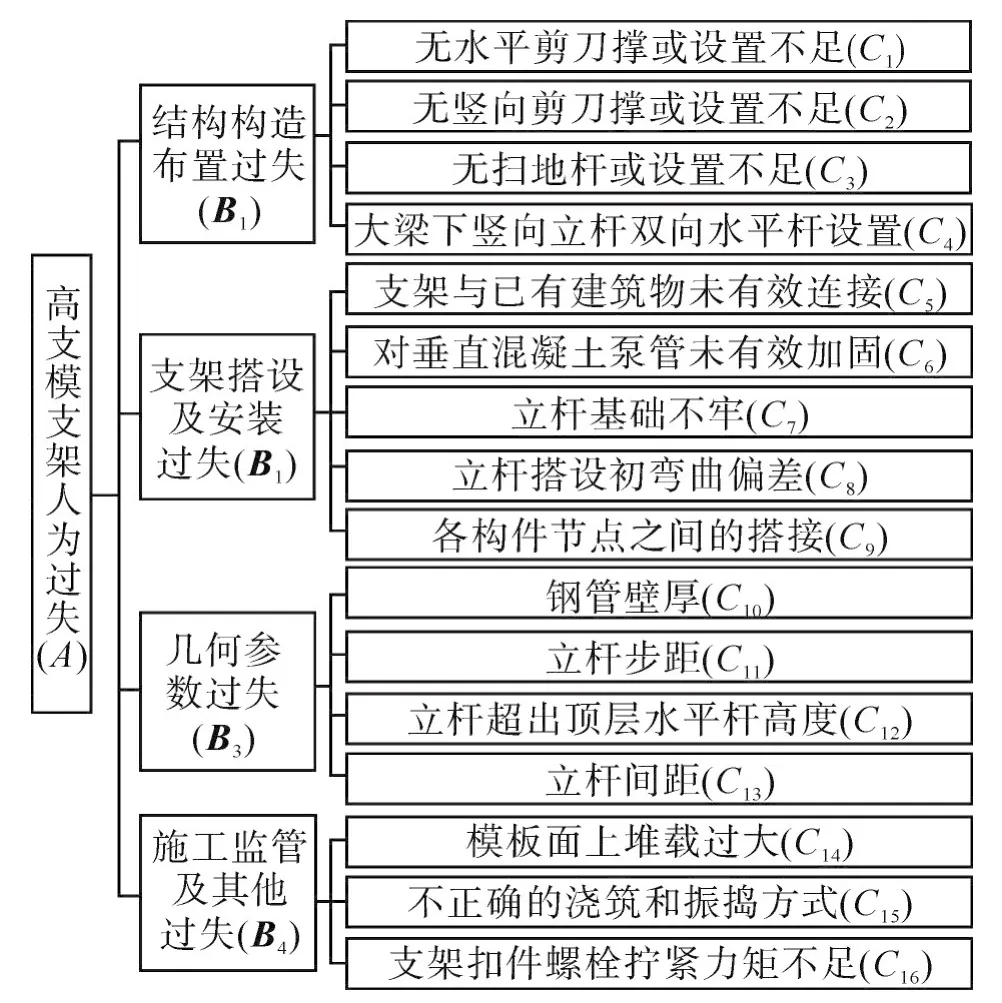
图1 考虑人为过失影响的层次结构体系图Fig.1 Hierarchical structure diagram considering the influence of human error

2 高支模支架人为过失影响因素的安全性评价

2.1 判断矩阵的构造

判断矩阵通过对相同层次中各因素相对于上一层中某一个因素的重要性程度的比较和评分得到[14]，比较评分分值设置如表1。

采取客观分析法对高支模支架中人为过失评分，综合各种因素及研究结论给出各层次评分见表2～6。

表1 高支模支架人为过失评价分值表Tab.1 Human error evaluation score table of high formwork support

表2 A-B评分表Tab.2 A-Bscore table

表3 B1-C评分表Tab.3 B1-Cscore table

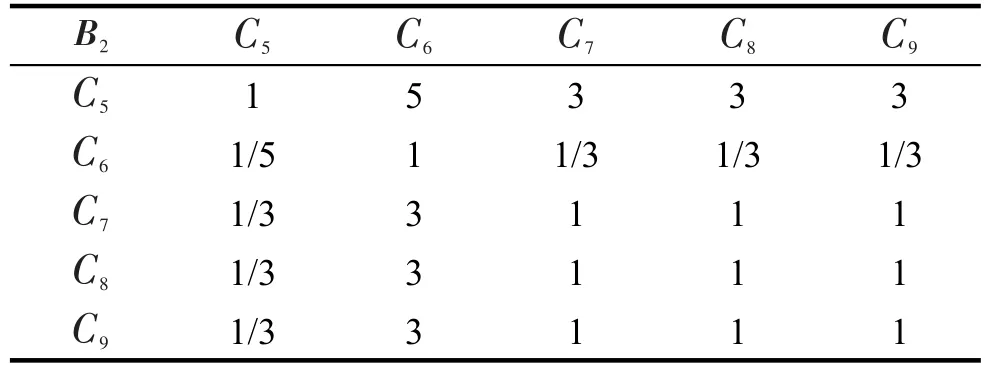
表4 B2-C评分表Tab.4 B2-Cscore table

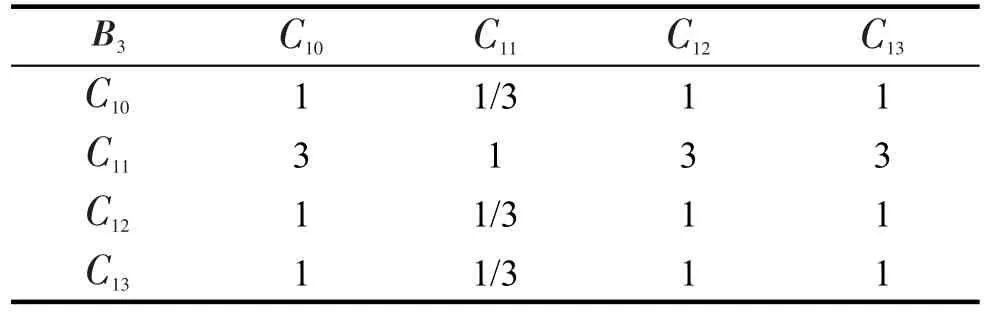
表5 B3-C评分表Tab.5 B3-Cscore table

由以上各评分表给出对应的判断矩阵分别为：

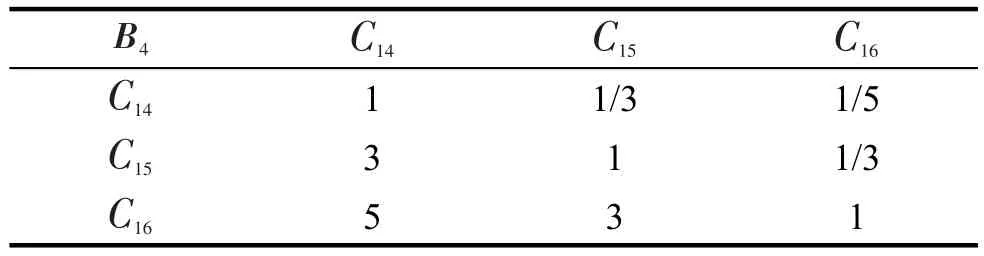
表6 B4-C评分表Tab.6 B4-Cscore table

2.2 层次单排序及其一致性检验

由上述矩阵A,B1,B2,B3,B4，求出对应的判断矩阵的最大特征值

其中：ω为A对应的特征向量；n为特征向量维数；(Aω)i表示Aω的第i个分量。ω可按以下方法求解：先将判断矩阵A的每一列归一化，得到新的矩阵方程B=(bij)n×n，再对矩阵B的行求和，即

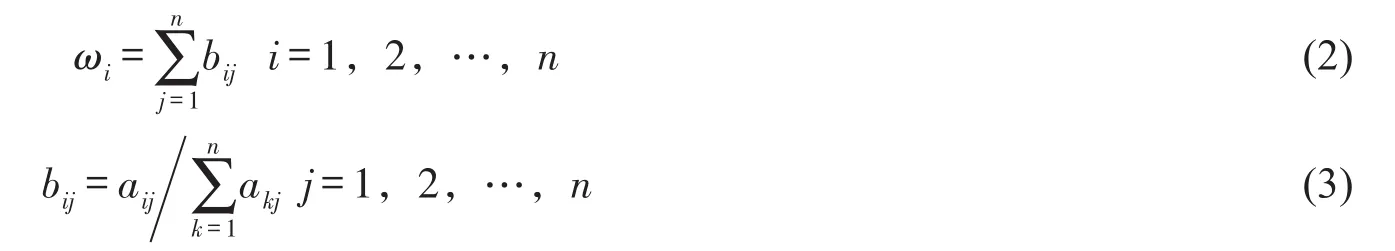
求出最大特征值λmax后，需对人为过失的判断矩阵进行一致性检验，检验的标准由一致性指标C表示，其计算式为

C=0表明判断矩阵完全一致，为理想的结果；C值过大，表明判断矩阵不一致程度大。故C需控制在一定范围内。为此引入随机一致性指标R。

满足式(5)时，判断矩阵A的一致性是符合要求的，否则，所求的判断矩阵需进行重新调整。随机一致性指标R的取值如表7。由式(1)～(5)，计算得层次单排序的计算结果及检验表(表8)。

表7 随机一致性指标R的取值Tab.7_ Values of random consistency index R

表8 层次单排序计算结果Tab.8_ Results of hierarchical single ranking calculation table

2.3 层次总排序

由表8中判断矩阵A特征向量ω分别与B1，B2，B3，B4，特征向量ω的乘积计算得到层次总排序，结果见表9。

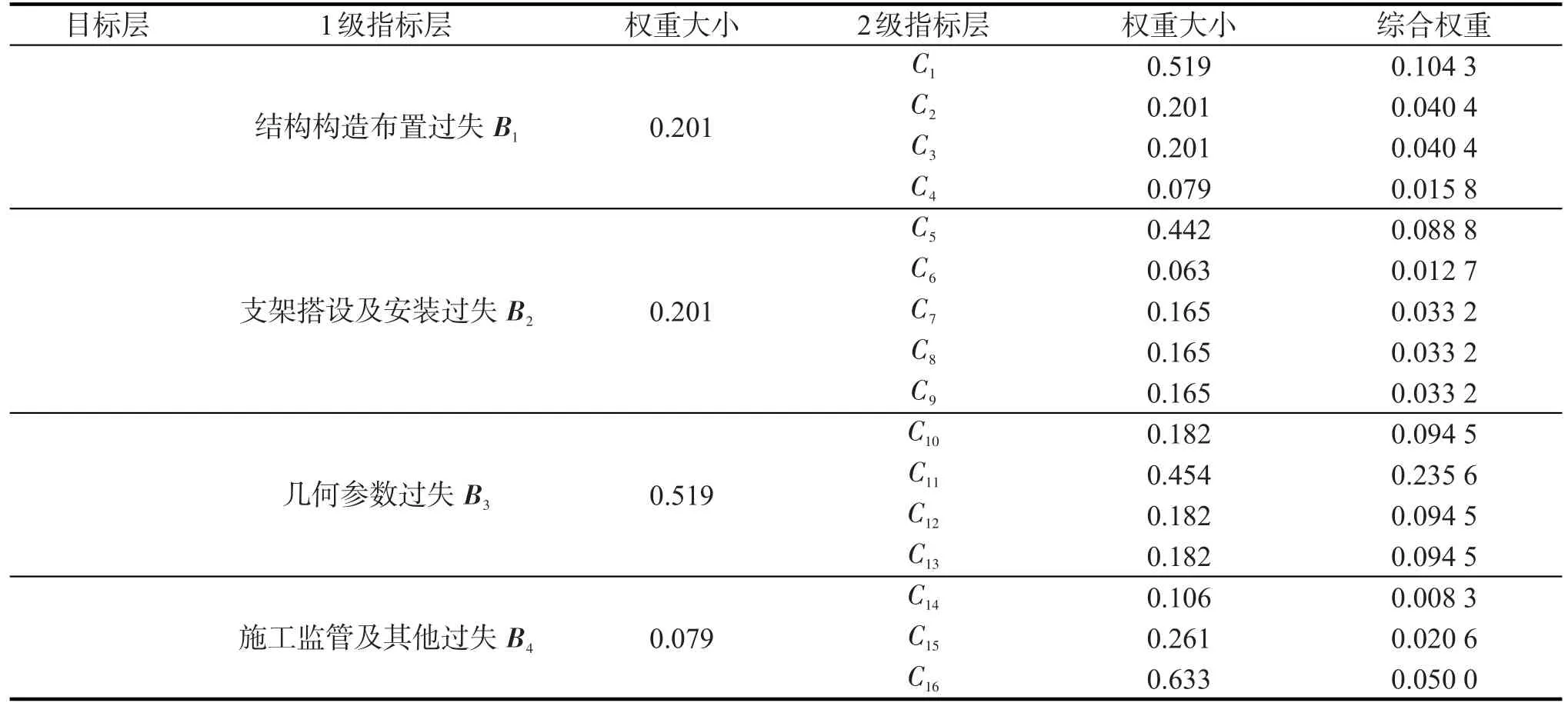
表9 层次总排序Tab.9 Hierarchical total ranking

2.4 结果与分析

为了更好地分析综合权重的排序情况，对总排序表中各人为因素的综合权重按由大到小排序，如表10。由表10可以看出：前9项人为过失的综合权重累积值达到0.843 0，接近0.85，占据较大比重，基本包含了最主要的人为过失。由表10中综合权重的大小可以得到，对高支模支架影响较大的人为过失依次为：立杆步距(0.235 6)→水平剪刀撑布置(0.104 3)→钢管壁厚(0.094 5)、立杆间距(0.094 5)、立杆超过水平杆长度(0.094 5)→支架与已有建筑物的有效连接(0.088 8)→支架扣件的拧紧力矩(0.050 0)→扫地杆布置(0.040 4)、竖向剪刀撑布置(0.040 4)。立杆基础、立杆初始弯曲、节点间搭核(0.033 2)综合权重反映其对高支模支架的安全性影响。模板面堆载(0.008 3)、混凝土泵的固定 (0.012 7)、双向水平杆设置(0.025 8)及不正确的浇捣方式(0.020 6)综合权重较小，对高支模支架的安全性影响相对较小。

表10 人为过失综合权重排序Tab.10_ Comprehensive weight ranking of human errors

3 人为过失对高支模支架安全性影响的数值模拟

3.1 高支模支架ANSYS模型的建立

为进一步分析人为过失对高支模支架的影响，在前述层次分析法结论的基础上，采用有限元ANSYS软件对高支模支架进行数值模拟[15]。有限元模型建立在高支模支架工程实例的基础上。对高支模支架底端采用全自由度约束；在顶端各节点处施加集中力荷载，荷载的总和为单位1；立杆和横杆均采用beam188单元，其属性参考beam188单元的性质设定；设置有剪刀撑和无剪刀撑两种支撑方式。基本参数如下：立杆步距1.50 m；梁纵向间距0.7 m，选取十跨；梁横向间距0.4 m，两跨；梁支撑架梁顶到地面搭设高度9.8 m；梁底7.3 m。

钢管类型为Φ48 mm×3.5 mm，其中钢管的弹性模量E=2.06×1011Pa，泊松比为0.3，密度为7 850kg/m3。建立的ANSYS模型(图2)及荷载约束(图3)。

3.2 高支模支架中人为过失数值模拟与分析

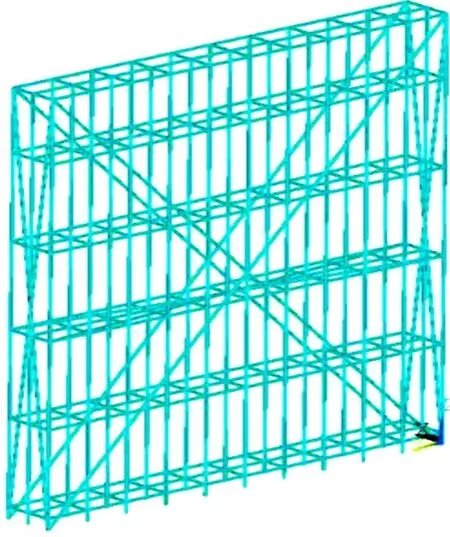
图2 高支模支架ANSYS模型Fig.2 ANSYS model of high formwork support

图3 高支模支架模型的约束及荷载布置Fig.3 Constraint and load layout of high formwork support model

数值模拟主要是对高支模支架体系进行屈曲分析，用于研究结构在特定载荷下的稳定性并确定结构失稳的临界载荷[16]。为保证数值模拟的准确性，文中对高支模有限元模型施加单位1的力，采用线性分析的方法，以模拟高支模支架在一阶屈曲分析时的屈曲荷载临界大小(即特征值屈曲),以此作为衡量高支模支架安全性能的指标。

模拟中人为过失分以下几种：立杆步距、剪刀撑布置、钢管壁厚、立杆间距、立杆顶端超过水平杆长度、扫地杆布置，分别考虑高支模支架有、无剪刀撑两种方式。限于篇幅，仅给出立杆步距对高支模支架安全性影响的有限元模型，其他组以表格给出模拟结果。

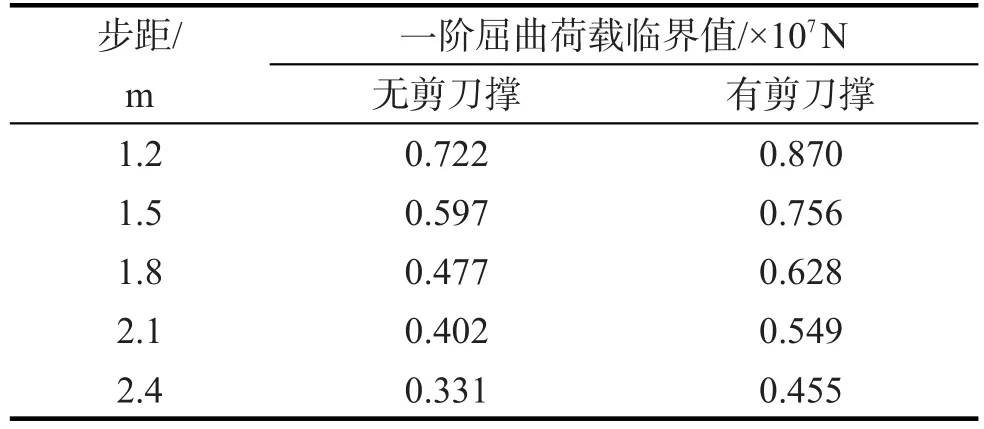
表11 不同步距数值模拟结果Tab.11 Numerical simulation results corresponding to different steps

3.2.1 立杆步距对高支模支架安全性的影响

设立1.2，1.5，1.8，2.1，2.4 m 5组步距，分别模拟其在有、无剪刀撑设置时的一阶屈曲受力和变形情况。其中，1.5 m步距条件下，施加荷载和约束后得到的一阶屈曲作用下的总体变形位移如图4。模拟所得一阶屈曲临界值见表11。

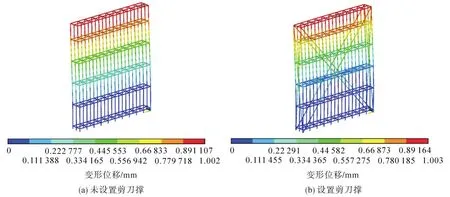
图4 高支模支架立杆1.5 m步距总体位移变形Fig.4 Overall displacement and deformation of 1.5 m step distance of the vertical bar for high formwork support

由表11可见：设置剪力支撑时,从实例模型的1.5 m步距到1.8，2.1，2.4 m，对应一阶屈曲荷载临界值分别减小了16.93%，27.38%，39.81%；相同步距条件下，未设置剪刀撑的支架比设置剪刀撑支架的屈曲荷载临界分别下降了17.01%，21.03%，24.05%，26.78%，27.25%。

3.2.2 钢管壁厚对高支模支架安全性的影响

设置Φ48mm×3.5mm，Φ48mm×3.2mm，Φ48mm×2.9 mm，Φ48 mm×2.6 mm，Φ48 mm×2.3 mm不同壁厚5组，模拟不同壁厚值钢管对高支模支架安全性的影响。在有、无剪刀撑两种情况下，模拟结果如表12。

由表12可见：设置剪力支撑时,壁厚为3.5，3.2，2.9，2.6，2.3 mm，对应一阶屈曲荷载临界值分别下降了7.54%，15.21%，23.02%，31.08%；在相同壁厚条件下，未设置剪刀撑组比设置剪刀撑组的屈曲荷载临界值分别下降了20.54%，20.79%，20.75%，20.87%，21.03%。

表12 不同壁厚值对应的数值模拟结果Tab.12 Numerical simulation results corresponding to different wall thickness values

3.2.3 立杆间距对高支模支架安全性的影响

在纵向总长度不变的情况下，对纵向立杆间距设置几组不同数值，设置纵向间距分别为：0.7 m十跨、1.0 m七跨、1.4 m五跨、1.75 m四跨4组。采用线性屈曲分析的方法，得到不同间距对应的一阶屈曲荷载临界值，见表13。

由表13可见：设置剪力支撑时,间距由0.7 m分别增大到1.0，1.4，1.75 m，其一阶屈曲荷载临界值分别下降了22.75%，38.49%，50.79%；相同间距条件下，未设置剪刀撑的各组相对设置剪刀撑的各组，一阶屈曲荷载临界值分别下降了21.03%，27.37%，29.89%，31.45%。

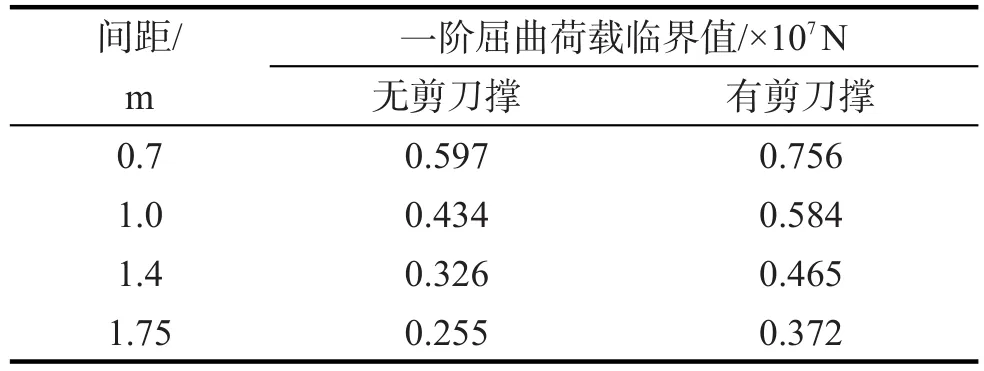
表13 不同间距值对应的数值模拟结果Tab.13 Numerical simulation results corresponding to different spacing values

3.2.4 扫地杆对高支模支架安全性的影响

设置0.2，0.4，0.6，0.8，1.0 m5组扫地杆高度，外加一组1.5 m高度(即不设扫地杆的情况)，对其进行线性屈曲分析，得到不同高度扫地杆条件下，高支模支架的一阶屈曲荷载临界值，结果如表14。

由表14可见：设置剪力支撑时,对应的扫地杆高度为0.2，0.4，0.6，0.8，1.0 m，一阶屈曲荷载临界值分别下降了7.14%，12.17%，17.0%，21.30%，26.19%；相同扫地杆高度条件下，未设置剪刀撑的各组相对设置剪刀撑的各组，一阶屈曲荷载临界值分别下降了21.03%，20.57%，20.18%，19.17%，19.15%，18.45%。

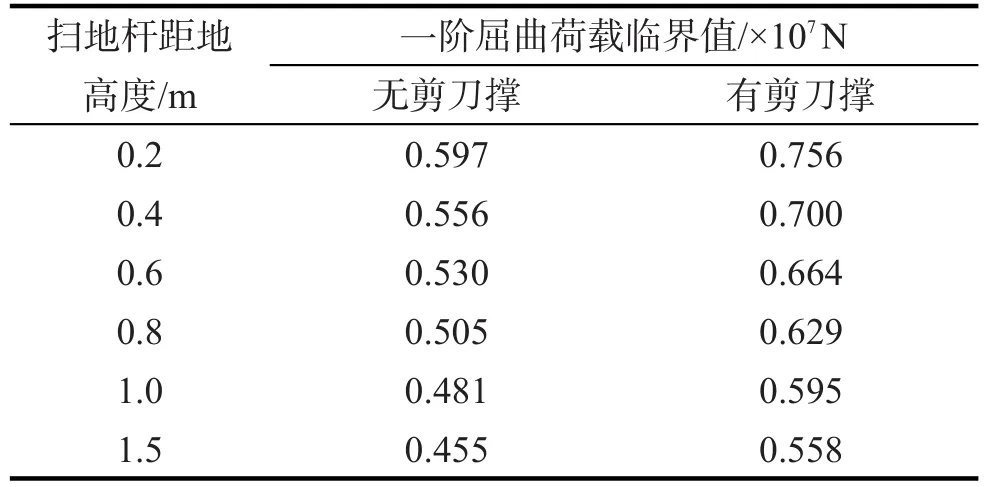
表14 不同扫地杆高度对应的数值模拟结果Tab.14 Numerical simulation results corresponding to different heights of sweeping rod

3.2.5 顶端伸出长度对高支模支架安全性的影响

设置0.2，0.4，0.6，0.8，1.0 m不同伸出长度。通过数值模拟得到不同顶端伸出长度对应的高支模支架一阶屈曲荷载临界值，结果如表15。

由表15可见：设置剪力支撑时,顶端伸出长度为0.2，0.4，0.6，0.8，1.0 m，各组对应的一阶屈服荷载临界值分别下降了5.19%，27.60%，54.23%，68.85%；相同顶端伸出长度条件下，未设置剪刀撑的各组相对设置剪刀撑的各组，一阶屈曲荷载临界值分别下降了21.82%，16.71%，5.0%，1.79%，1.75%。

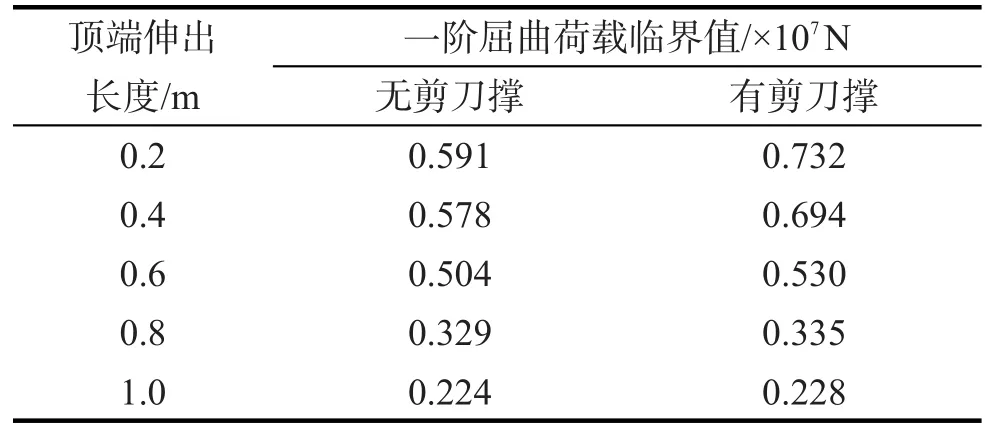
表15 不同顶端伸出长度对应的数值模拟结果Tab.15 Numerical simulation results corresponding to different top extension lengths

3.3 结果比较

分析有、无剪刀撑两种情况模拟结果，可以看出：当设置剪刀撑时，立杆步距、钢管壁厚、立杆间距、扫地杆高度、立杆顶端超过水平杆长度各组中一阶屈曲荷载临界值降低最多分别为39.81%，31.08%，50.79%，26.19%，68.85%，上述人为过失对高支模支架影响的排序情况为：立杆顶端超过水平杆长度→立杆间距→立杆步距→钢管壁厚→扫地杆布置；未设置剪刀撑与设置剪刀撑相比，立杆步距、钢管壁厚、立杆间距、扫地杆高度、立杆顶端超过水平杆长度各组一阶屈曲荷载临界值下降最多分别为27.25%，21.03%，31.45%，21.03%，21.82%，上述人为过失对高支模支架影响的排序情况为：立杆间距→立杆步距→立杆顶端超过水平杆长度→钢管壁厚、扫地杆布置。