基于深度信念网络的供应链柔性提升

孔繁辉，李 健,2

(1.天津理工大学 循环经济与企业可持续发展研究中心，天津 300384；2.天津大学 管理与经济学部，天津 300072)

0 引言

面对商业环境日益增强的不确定性与复杂性,企业需要通过不断降低提前期、转换生产步伐来提升自身竞争力。企业的运作能力依赖于高效的供应链柔性网络。Slack[1]提出供应链柔性的概念，指出供应链柔性是供应链中成员根据市场环境及时做出响应的能力，提高供应链柔性是企业提高不确定性环境下反应速度的重要表现。因此，提升供应链网络柔性对提高企业的运作效率有重要作用。

柔性供应链面临的主要风险主要来自供给端、需求端和中间层的不确定性。供给端的不确定性来源于供应节点的不确定性；需求端的不确定性来源于需求量的不确定性；中间层的不确定性来源于时间和运输成本的不确定性。目前，国内外学者对供应链中的不确定性进行了研究。针对供给端的不确定性，Snyder等[2]在供应链不确定的情况下，提出两种选址模型，解决了供应商选址问题；在此基础上，Chanta等[3]运用改进的环境管理系统优化多种不确定因素，解决了供应端面对不确定处境的优化问题。针对需求端的不确定性，Hatefi等[4]将供应链不确定性风险进行分类，认为第二类风险是影响需求量的决定因素；Amin-Naseri等[5]则研究两个供应链成员通过确定需求量来控制价格竞争模型。综上，供应端不确定主要是中转点选择问题，而需求端不确定性主要是流量分布问题。

值得注意的是，大部分学者只研究了供应端或需求端的某一种不确定性，很少有人综合考虑供应端与需求端的双重不确定性，只有Song等[6]和Kazaz等[7]同时考虑供应链中的供求双重不确定性，提出通过建立一种随机规划模型，对两个端点的不确定性进行优化，然而最后的算例结果并不很理想。在以上研究的基础上，本文首次运用网络模型，对供应链柔性网络的提升问题进行研究。

深度学习是一种有效的机器学习模型，与其他机器学习模型(人工神经网络、回归分析等)不同，深度学习包含有更多隐层，更能抽象数据的本质特征[8]。作为深度学习中最为典型的算法，深度信念网络(Deep Belief Network, DBN)在供应链网络研究中有天然的优势。DBN在模式分析过程中描述观察到的数据的高阶相关属性，或者描述数据及其相关类别的联合概率分布。与传统的BP神经网络需要对数据进行标签不同，DBN不关心数据的标签，经常使用非监督性特征学习[9-10]，被广泛应用于图像数据分类、语音识别等领域[11-13]。本文首次将该算法应用到供应链柔性研究领域，并把此算法与BP神经网络进行详细对比发现，较BP神经网络训练方法，DBN的显著优势是在处理供应端节点选择和需求端流量分步时能更加及时准确地抽象出数据标签[14-16]，大大提升了供应链面临风险时的决策响应速度。

因此，本文运用全新的DBN模型，在综合考虑供应链中供应端不确定因素(节点中断的可能性)和需求端不确定因素(需求量的波动)的前提下，以提升供应链柔性网络为目的，将DBN与传统的BP神经网络进行对比，对发生供应链不确定风险时的中转点选择与流量分布进行了优化，最后用案例对模型进行验证。测算结果表明，DBN比传统的BP神经网络具有更强的学习训练能力，对构建供应链柔性网络有更有效的提升空间，从而提高了企业响应不确定风险的反应速度。

1 问题描述

本文构造一个用G(V,A)表示的供应链柔性网络。其中：V表示供应链网络结构中的所有节点集合，节点主要由供应点、中转点与需求点构成[17](如图1)，为了便于分析，引入虚拟起点、虚拟中转点与虚拟终点，构成了一个闭合供应链网络，即V{Si,Ti,Tri,Di}；A表示所有节点相连线路的集合。

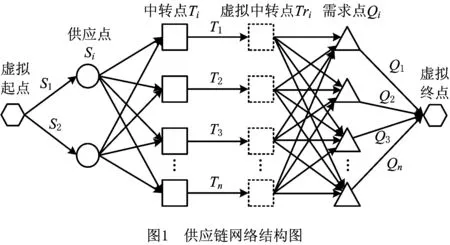
供应链柔性不仅受到节点中断风险的威胁，本文还考虑了需求波动风险对供应链柔性网络的影响。作为供应链网络的起点，供应点正常运行与否直接关系到整个系统能否正常运行，因此在企业的实际运营管理中，对供应点Si的保护力度较其他节点大得多。鉴于现实中供应点中断的概率很小，本文着重考虑中转点Ti与Tri发生中断的情况。另外，该供应链网络结构中供应点的供应能力是有限的，即S1与S2的和为定值，决策者需要从一些有设施容量限制和固定成本的中转点Ti与Tri中选出合适的节点来建设供应点。

在节点选择过程中，需要考虑多种因素对供应链成员的影响，这些因素包括运输成本、可变成本、固定成本。成本越小，供应链成员的利润越高[18]。本文采用非线性混合布尔规划方法建立数学模型。

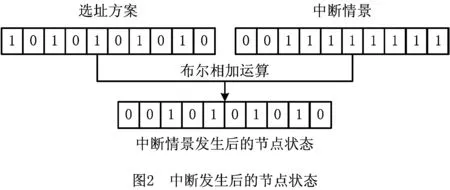
供应链网络结构中，中转节点只有开放或关闭两种状态，分别用0和1表示，0表示关闭，1表示开放。若候选的中转点数为10，则用一个长度为10的布尔字符串表示供应链网络结构的一种选址方案，例如X={1111100000}表示只有中转点1,2,3,4,5被选中，选中的中转点为开放状态，其他中转点为关闭状态。

如图2所示，中转节点的状态是选址方案和中断情景进行布尔相加的结果。对于中断情景，若Y={0011111111}表示1,2号候选中转点处发生了中断，导致这两处的中转点不能再运行，则整个供应链节点状态变为Z={0010101010}，表示3,5,7,9中转点正常运行，其他节点处于关闭状态。

2 建立供应链柔性网络模型MODEL(P1&P2)

在建立供应链柔性网络模型中，本文定义了建立模型需要使用的参数与符号,如表1所示。

表1 相关参数与符号

在中断情景为S、需求情景为e的前提下，最优网络总成本由中转点的固定成本和产品的运输成本两部分构成，即

Kse=min{∑fiNi+∑uijYijse}。

(1)

中断场景s中的每一种场景都有其对应的网络成本，要求网络成本的集合中超过K1的比例不能超过P1。同时，若在中断场景确定的情况下，需求场景e中的每一种场景也有自己对应的网络成本，则要求网络成本的集合中超过K2的比例不能超过P2，即

P{K2>K1}≤P1;

(2)

P{Kse>K2}≤P2。

(3)

P1和P2表示决策者的风险偏好，其值越大，说明决策者的风险偏好趋于乐观，当P1=1，P2=1时，表明决策者不相信任何不确定情况会发生，所设计的网络达到最精益的状态；P1与P2的值越小，说明决策者的风险偏好趋于保守，当P1=0，P2=0时，表明决策者已经做了最坏的打算，所构建的网络达到了最为冗余的状态。

另外，网络流量有最大流量值限制，这是本文建立数学模型的前提条件。中转节点只有0和1两种布尔状态，即关闭和开放两种状态表示为

(4)

3 基于深度信念网络的供应链柔性网络构建原理

在供应链柔性衡量问题中，有容量限制的柔性网络问题非常复杂，对于这类问题，国内外学者多用BP神经网络算法求解，然而计算过程中的复杂性使BP神经网络实时更新数据的能力非常有限,算法存在一定的局限性[19]。

本文引入一种有效的深度学习中的典型算法DBN。深度学习是机器学习中的一种对数据进行表征学习的方法，该方法通过学习一种深层非线性网络结构来表征输入数据，实现复杂函数逼近，具有强大的、从少数样本集中学习数据集本质特征的能力。作为深度学习的训练算法，DBN的目的在于通过建立、模拟人脑来分析学习数据特征。与传统的BP神经网络只有单一隐层相比，DBN含有多个隐层，因此具有更强的特征提取与学习能力，克服了对有限数据的依赖。DBN可以通过多个逐层数据特征变换，将样本空间表示为一个新特征空间，从而使数据特征分类更正确。

DBN可以简单理解为传统BP网络的拓展。DBN与传统的BP神经网络都由输入层、隐层、输出层构成，而且分层结构之间只有相邻层节点有连接，跨层节点之间相互无连接。不同之处在于，BP神经网络的隐层是单层结构，DBN具有多层隐层，多层隐层可以保证将模型中的特征向量映射到不同的特征空间，从而保留更加准确的特征信息，克服了BP神经网络容易陷入局部最优和训练时间过长的缺陷。DBN的整体框架如图3所示。

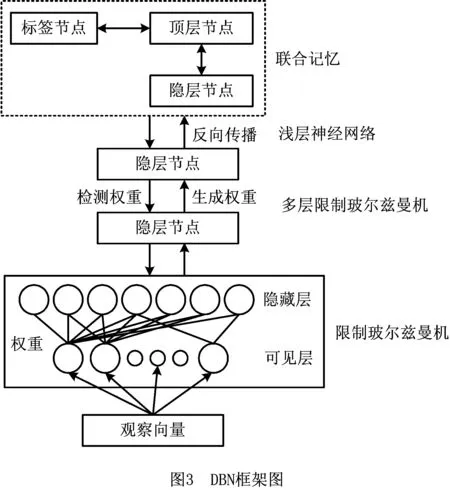
因为该模型是多部图，所以在已知输入数据层v的情况下节点之间不存在连接，所有隐层节点之间是条件独立的，即p(h|v)=p(h1|v)…p(hn|v)。同理，在已知隐层h的条件下，所有可视层中的节点是条件独立的。因为所有的v和h都满足玻尔兹曼机分布，所以当输入v时，通过p(h|v)可以得到隐层h和下一个可视层。不断调整参数，使从隐层得到的可视层v1与原来的可视层v一样，该隐层即为可视层的另外一种表达。因此，隐层可以作为可视层输入数据的特征。

此时，联合组态可以表示为

E(v,h,θ)=

(5)

θ={W,a,b}。

(6)

某个组态的联合概率分布可以通过玻尔兹曼机分布(和该组态的能量)确定：

(7)

(8)

隐藏层节点之间是条件独立的(因为节点之间不存在连接)，即

(9)

对式(9)进行因子分解，得到在给定可视层v的基础上，隐藏层第j个节点为1或为0的概率

分析基于DBN的中转点实时选择及流量分布策略内容，DBN需要严格的网络输入数据和输出数据，网络输入为含有(A+B)×N个元素的整数向量，W1，W2，W3分别为供应点、中转点和需求点的权重，通过微调3个权重的贡献度对模型进行调整。网络输出为十进制数2N(表示N个元素的二值向量)，为中转点开合情况的具体体现。网络训练实施步骤如下：

步骤0数据准备阶段。提取已有的鲁棒网络数据，分为供应点、中转点和需求点3部分。在中转点部分使用布尔变量表示此处的开合状态，即0表示关闭，1表示开放。

步骤1输入训练集数据。将供应点和需求点的(A+B)个数据作为样本输入到DBN中，辅以十进制数作为样本标签。其中：A表示供应点数，B表示需求点数，N表示中转点数。

步骤2训练阶段。在网络生成中，一个重要的任务是预训练。当训练数据有限时，学习较低层的网络是比较困难的。因此，一般采用先学习每一个较低层，再学习较高层的方式，通过贪婪地逐层训练，完成从底向上分层学习。

步骤3网络形成。经过较为充足的样本输入后，整个DBN趋于平衡，网络中的各项参数与中转点预想结果匹配。输入测试集中无标签的数据，多次训练直到网络模型是鲁棒的，此时的输入量(A+B)即为供应点和需求点的最终成本分布结果。

步骤4测试数据输出。数据结论以十进制数2N的形式展现。将十进制数转化为二进制数值后，每个节点上呈现的结果即为中转点需要开合的状态。

步骤5在确定中转点选择方式后，将开放的中转点重新编号，即将原有的N个候选中转点减少到M个，则整个供应链网络流量部分涉及(A+B+1)×M个数据。本文采用线性同余法产生随机数据，放入网络中。

步骤6将工作回报值增加到原来的110%，即人为定义其误差损失为10%。算法通过最优化各层神经元的输入权值和偏置，使网络的输出尽可能地接近期望输出，以达到训练或者学习的目的。按照相应的位置提取(A+B+1)×M个数据，即为在一定中转点选择方式条件下的最优流量规划策略。

根据上面建立的模型MODEL(P1&P2)及网络训练步骤，本文基于机器学习中的DBN对供应链柔性网络构建问题进行设计，在此基础上将DBN的训练结果与传统BP神经网络进行对比，最大程度地优化网络模型，得到在供应端和需求端不确定风险下的供应链柔性网络。

4 实例分析

以某大型制造企业为例，该企业有2个供应商I(成都、上海)，表示为I1，I2；有9个中转点J(北京、呼和浩特、西安、沈阳、南昌、武汉、长沙、杭州、合肥)，表示为J1～J9；有10个需求点M(广州、昆明、南宁、福州、贵阳、上海、济南、太原、兰州、银川)，表示为M1～M10。波动集合{e1,e2,e3,e4,e5}是随机选取的5种需求状态，S对应10个需求点的网络流量，如表2所示，表中estd为平均需求值。

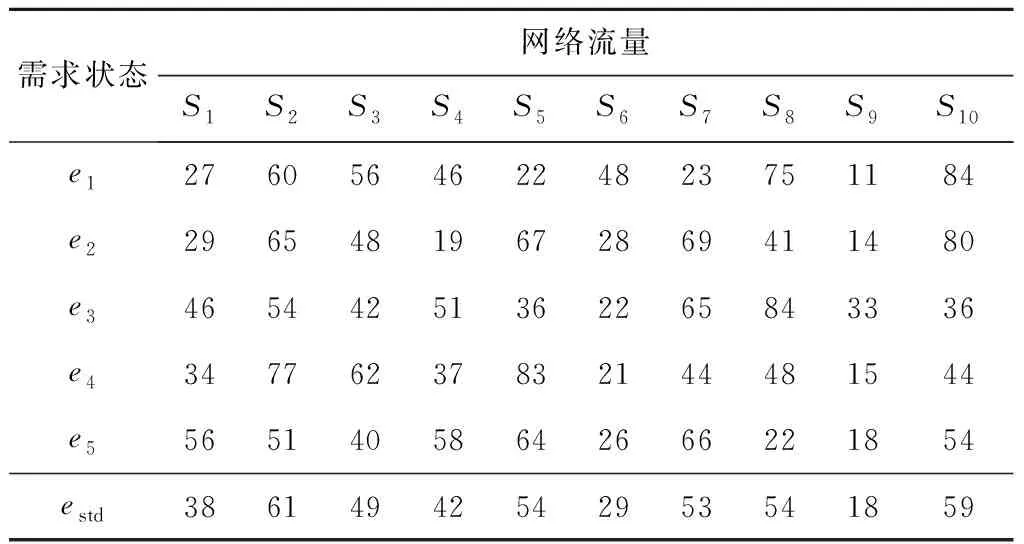
表2 需求节点波动情景

在中转点选择和流量优化过程中，需要考虑实际配送中多种因素的影响，针对供应链网络的复杂性，本文重点选取8个指标因素对中转点选择和流量分布进行测算，这8个指标分别是快速反应能力、配送保障能力、运输效能、技术设备、通讯条件、经营环境、节点面积、最大容量。因为这些指标既有定量指标又有定性指标，所以针对不同的指标因素采用不同的隶属度函数来确定各个指标的等级隶属度。

4.1 供应链柔性网络预处理——基于遗传算法的中转点选择

供应链中转点选择问题的研究成果较为丰富，已经形成了相对成熟的算法，实际生产中多应用遗传算法对中转点进行选址，鉴于这类问题的改进空间较小，本文使用遗传算法对供应链中转点进行预处理。

模型目标为总成本C最小，总成本包括配送成本、运营成本和变动成本，建立以下数学模型：

目标函数：

s.t.

(12)

y(j,m)=0,1∀m,j=1,2,…,J。

(13)

式中：I和J分别表示供应点与中转点数量；p为中转点的最大数量；xij为供应点i到中转点j的运输量；y为流转单价；cij为从供应点i到中转点j的运输单价；vc为中转点到需求点的运输单价；pi为中转点i的容量，如果中转点i被选中，则网络流量不能超过中转点的流量限制；Dm表示m地的需求量，从中转点向需求点供应的总量应大于需求点的需求数量。目标函数是从中转点选出最佳的配送中心，使配送成本、运营成本和变动成本的总成本最小。

I1与I2的最大供应能力为1 000t和800t，供应点到9个中转点的配送费率为0.55元/(km·t),I1与I2到中转点J1～J9的行驶距离以及供应点到需求点M1～M10的行驶距离如表3和表4所示。

表3 供应点到中转点的行驶距离

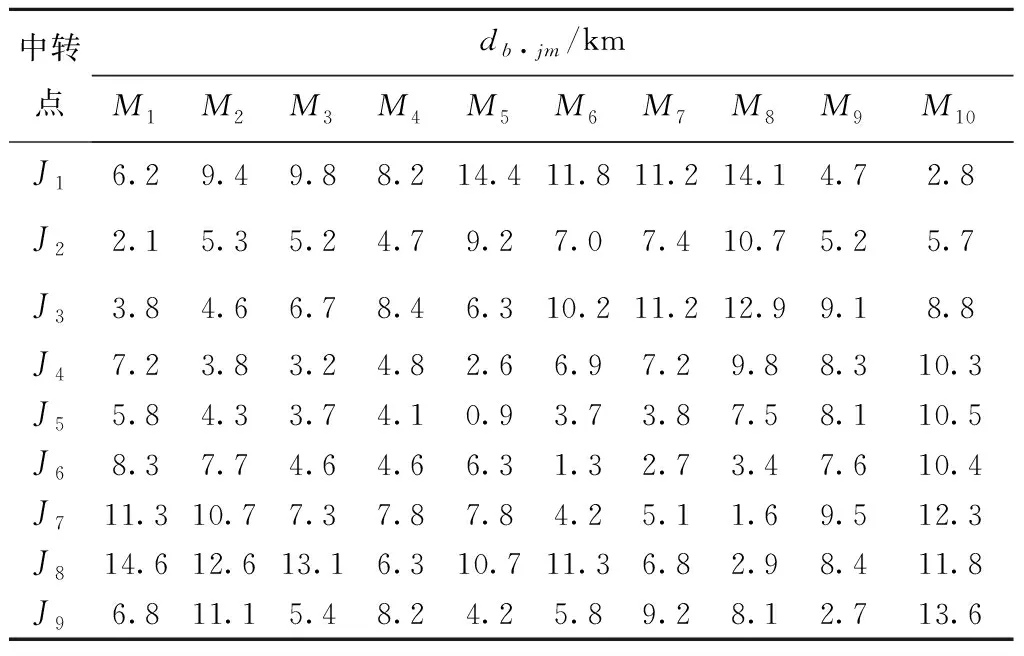
表4 中转点到需求点的行驶距离

中转点的成本主要包括配送成本、运营成本和变动成本3方面，分别用Cb，C1，VL表示。9个中转点的详细建设费用、运用费用和容量限制如表5所示。

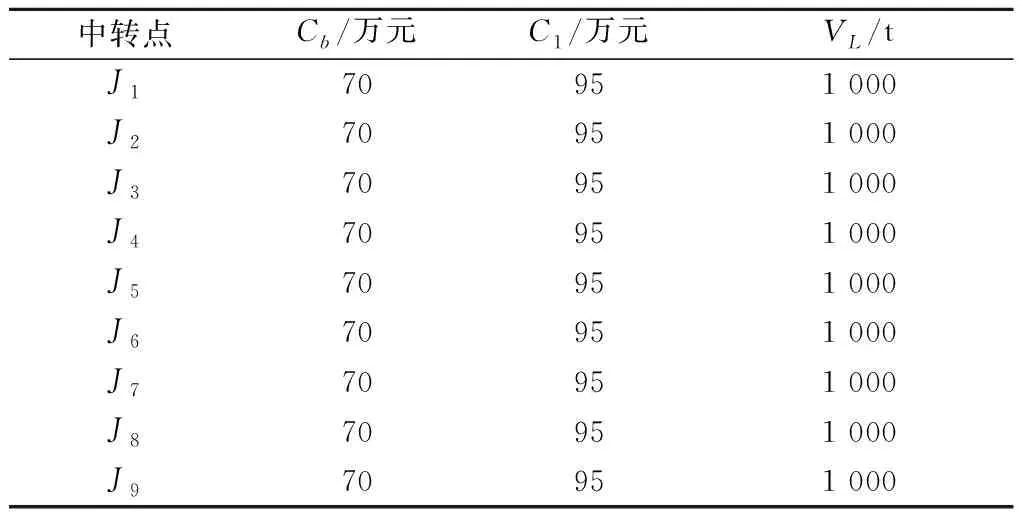
表5 中转点费用及容量限制

为了说明决策者在不同风险偏好组合下对选址的影响，本文对风险偏好参数进行设置，并进行分析。在实际生产过程中，决策者对供应点波动持有乐观的态度，这是由于供应点具有可控性，决策者往往对自己可控的因素比较乐观；然而，需求点的波动情况是不可预知的，也是无法控制的。换言之，决策者对供应端的预期趋于乐观，而对需求端趋于保守。

根据上文所述，设置P1=0.5,0.7，0.9，P2=0.1，0.3，0.5。在这组数据条件下进行实验，得到最优的节点选择结果，如表6和表7所示。

表6 选址结果

表7 收益结果

从表6得到的选址结果来看，当决策者的风险偏好发生变化时，网络的选址结果也会相应变化。在最保守条件下的选址结果为9个城市，乐观条件下的选址结果减少为6个。因此，选址结果与决策者的偏好密切相关。

由表7可知，决策者在乐观参数约束下能够得到更多的收益，而在保守原则的指导下会降低收益。然而，生产过程中如果供应链网络出现波动，则前者的抵抗能力会非常弱，很容易承受巨大的经济损失，而保守条件下的选址结果可以帮助企业渡过暂时的困难。因此，制造型企业应该采用参数P1和P2对决策进行约束，在这两者之间找到一个平衡点。

4.2 BP神经网络流量预测

在确定中转点后，需要对供应链网络流量分布进行优化。中转点选择是对流量进行分布的前提，在网络流量分布优化之前，每个中转点间的流量分布总是按经验主义随机分配,即流量分布先有初始的分布状态[20]。

搜集已有的数据，前10个方案是公司的历史数据(9月份)，这10组历史数据为本文的训练方案，后10个方案为待处理方案(10月份)，通过对所有原始数据进行量化模糊测算后，得到8个指标具体的量化训练数据，各个训练数据虽然存在一定差距，但各个线路流量分布值在0～1之间变动。各个指标的具体量化数据如表8所示。

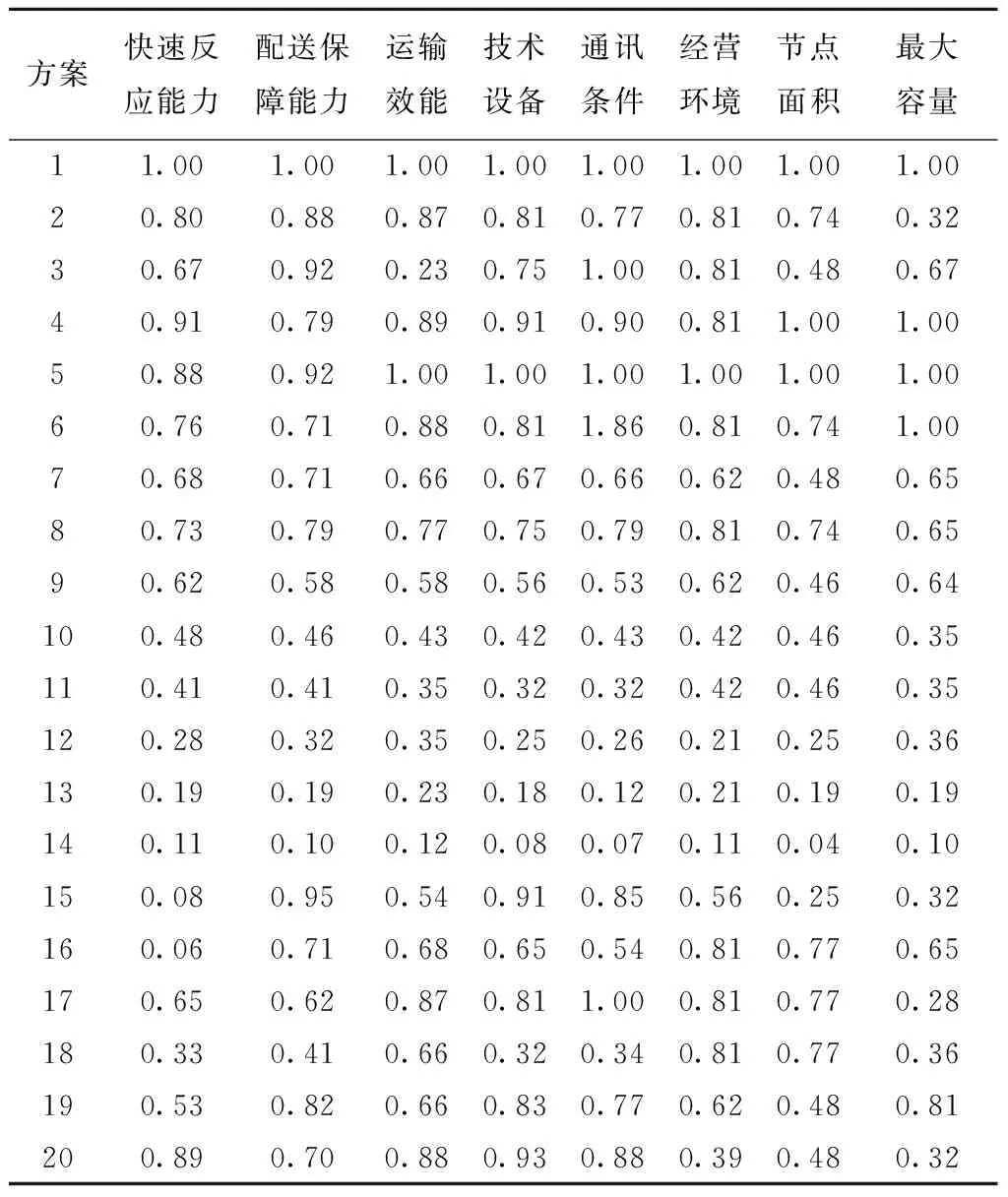
表8 指标量化训练数据

因为BP神经网络只有单一的隐层，所以网络学习能力较低，特别是对大量数据训练以后，网络拟合度将降低。隐层中共有8个神经元，输出层为1个神经元。将表8前10个方案的样本数据作为初试类进行600次学习训练。

专家采用德尔菲法对表8中的前10个方案样本数据进行评估，然后将BP网络输出的后10个方案训练结果与专家的评估结果进行比较，如表9所示。

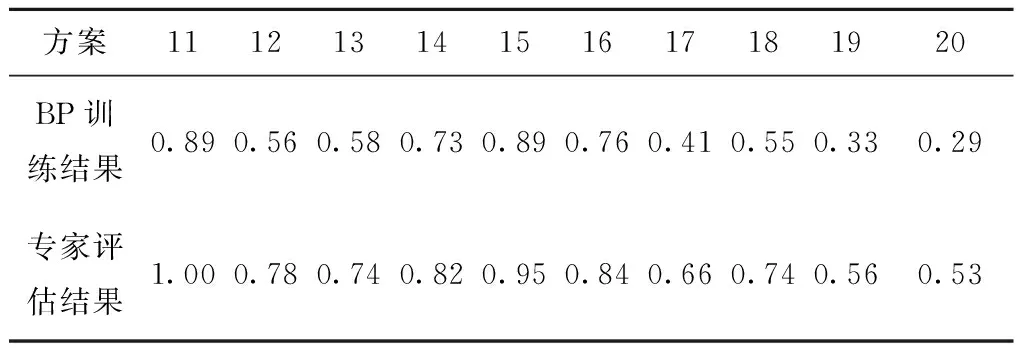
表9 训练输出结果与专家评估的比较

4.3 深度信念网络流量预测

与传统BP神经网络不同，DBN含有多个隐层，其对数据拟合能力更强，而且DBN对训练数据的本质特征没有要求，模型可以通过组合低层特征形成更加抽象的高层表示，从而实现复杂函数的逼近。采用MATLAB软件对表8的样本数据进行600次训练，并将其输出结果与专家评估结果进行比较，如表10所示。

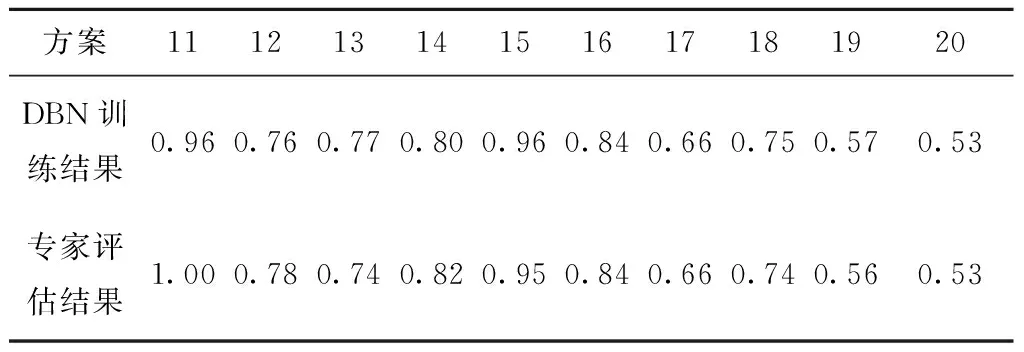
表10 训练输出结果与专家评估的比较

为了论证DBN流量预测的有效性，对DBN算法的适用性进行检验。节点流量分布的置信区间和显著性检验结果如表11所示。

表11 样本检验结果

由表11可见，所有输出的检验样本与专家评估结果的接近程度均在96%以上，表明经过样本数据训练，DBN模型完全可以脱离专家的辅助，在处理大量样本数据及实时流量分布优化上显示出明显的优势。因此，只要对历史数据进行学习训练，该模型就可以为供应链网络选出最优的流量分布方案，从而表明该方法可为大型制造企业构建供应链柔性网络提供参考。

4.4 BP神经网络与深度信念网络对比分析

将表9与表10进行对比分析可以发现，BP神经网络对样本的预测结果与专家评估结果之间存在较大的差异，其预测准确性明显低于DBN。表12所示为BP神经网络与DBN的预测平均值对比分析结果。

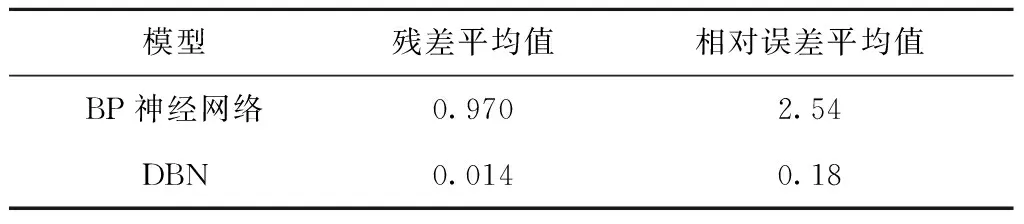
表12 模型训练结果对比

由表12可知，DBN的残差平均值和相对误差平均值分别为0.014和0.18，远小于BP神经网络，两种训练结果的准确性差异明显，DBN的训练结果更加接近专家的评估结果。因此，DBN在预测供应链柔性网络的流量时有明显的优势。在供应链管理中，时间作为重要的因变量是决定供应链柔性的主要参数。因此，除了考虑模型结果的准确性外，还需要对模型网络的迭代次数和迭代时间进行比较。两个模型的具体对比情况如表13所示。

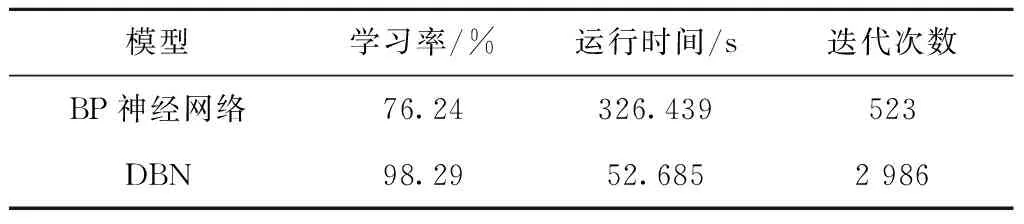
表13 模型训练时间对比

供应链网络流量实际值与两种算法的预测流量值如图4所示。可以看出，DBN的流量预测结果比BP神经网络的流量预测结果更接近实际流量。图5说明DBN的预测误差随着训练次数的增加逐渐趋于零，BP神经网络的预测误差明显高于DBN的预测误差。

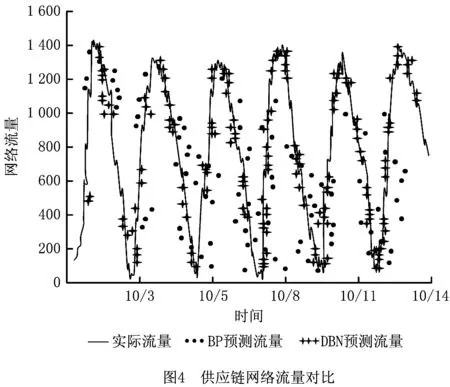
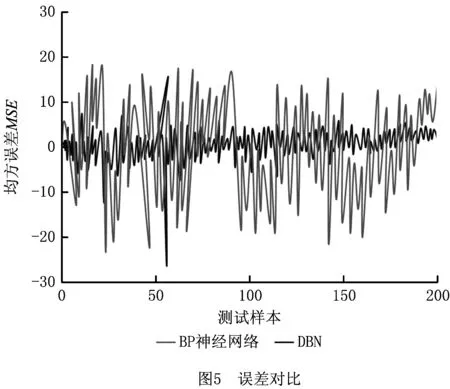
在以上对BP神经网络和DBN对比过程中，初始参数完全相同，均基于遗传算法的供应链网络节点选择结果，通过对比预测结果的准确性和模型训练时间两方面可知，DBN比BP神经网络具有更高的预测精度和更短的网络训练时间。

由于数据量过大，导致BP神经网路的模型泛化能力降低、训练时间增长，出现过度拟合的问题。DBN通过对大量数据的多次迭代可以确保训练结果的准确性，虽然迭代次数增加，但是训练时间并未延长，因而提高了网路学习率和收敛速度。由此可见，DBN能够有效克服传统BP神经网络的缺陷，构建供应链柔性网络的最优模型。

5 结束语

随着市场的不断变化与竞争的加剧，构建供应链柔性网络对制造业具有重要的意义。供应链柔性网络不仅可以缩短企业处理不确定风险的响应时间，还可以为企业生产节约成本，保证企业各项业务的正常运转，从而提高企业的生产运营效率。结合实际情形，本文考虑了节点中断和需求波动双重不确定性给企业决策造成的影响，运用DBN克服了传统BP神经网络数据预测的缺陷。DBN不但在预测结果中表现出了更高的精度，而且在学习率、运行时间和迭代次数等方面，也表现出较强的能力。更为重要的是，DBN能够对复杂系统中的非线性关系进行更加精确的训练，因此能够在复杂非线性条件下准确预测供应链中的网络流量分布。通过实例分析发现，相比传统BP神经网络，DBN在训练样本数据时的拟合精度更高；另外，供应链柔性网络比确定网络在面临不确定风险时更有优势。

对于具有最优学习率的DBN来说，未来还可以对其进行完善，例如如何确定最优的隐层节点数，怎样将模型精度进一步提高等，这些都可以成为今后研究的方向。

参考文献:

[1] SLACK N. The flexibility of manufacturing systems[J]. International Journal of Operations & Production Management,2005, 25(25):1190-1200.

[2] SNYDER L V, DAKIN M S. Reliability models for facility location:the expected failure cost case[J]. Transportation Science,2005,39(3):400-416.

[3] CHANTA S, MAYORAL M, MCLEAY L. Improving emergency service in rural areas:a bi-objective covering location model for EMS systems[J]. Annals of Operations Research,2014,221(1):1-27.

[4] HATEFI S M, JULIA F. Robust and reliable forward-reverse logistics network design under demand uncertainty and facility disruptions[J]. Applied Mathematical Modeling,2014,38(9/10):2630-2647.

[5] AMIN-NASERI M R, KHOJASTEH M A. Price competition between two leaders-follower supply chains with risk-averse retailers under demand uncertainty[J]. International Journal of Advanced Manufacturing Technology,2015,79(1/2/3/4):377-393.

[6] SONG J S, YANO C A, LERSSRISURIYA P. Contract assembly:dealing with combined supply lead time and demand quantity uncertainty[J]. Manufacturing & Service Operations Management,2000,2(3):287-296.

[7] KAZAZ B, WEBSTER S. The impact of yield-dependent trading costs on pricing and production planning under supply and demand uncertainty[J]. Manufacturing & Service Operations Management,2011,13(3):404-417.

[8] GHAHABI O, HERNANDO J. Deep belief networks for i-vector based speaker recognition [J]. IEEE International Conference on Acoustics , 2014, 4 (2): 13-22.

[9] LI Jing, LI fangyi, ZHOU Lirong, et al. Sensitivity analysis of product life cycle assessment based on BP neural network[J]. Computer Integrated Manufacturing Systems, 2016, 22(3):666-671(in Chinese). [李 静,李方义,周丽蓉,等.基于BP神经网络的产品生命周期评价敏感性分析[J].计算机集成制造系统,2016,22(3):666-671.]

[10] FANG Bopeng, SUN Linfu, TANG Huijia. The core competence of industrial chain based on self organizing I/O mapping neural network [J]. Computer Integrated Manufacturing Systems, 2016,22(1):33-54(in Chinese). [方伯芃,孙林夫,唐慧佳.基于自组织I/O映射神经网络的产业链核心竞争力[J].计算机集成制造系统,2016, 22(1):33-54.]

[11] BROSCH T, TAM R. Efficient training of convolutional deep belief networks in the frequency domain for application to high-Resolution 2D and 3D images[J]. Neural Computation,2015,27(1):1-17.

[12] JI N, ZHANG J S, ZHANG C X. A sparse-response deep belief network based on rate distortion theory[J]. Pattern Recognition,2014,47(9):3179-3191.

[13] NAGARAJAN V, SAVITSKIE K, RANGANATHAN S, et al. The effect of environmental uncertainty, information quality, and collaborative logistics on supply chain flexibility of small manufacturing firms in India[J]. Asia Pacific Journal of Marketing & Logistics,2013,25(5):784-802.

[14] LUMMUS R R, DUCLOS L K, VOKURKA R J. Supply chain flexibility:building a new model[J]. Global Journal of Flexible Systems Management,2003,4(4):1-13.

[15] RUEKERT R W, CHURCHILL G A. Reliability and validity of alternative measures of channel member satisfaction[J]. Journal of Marketing Research,1984,21(2):226-233.

[16] GHASEMI F, FASSIHI A, PÉREZ-SNCHEZ H, et al. The role of different sampling methods in improving biological activity prediction using deep belief network[J]. Journal of Computational Chemistry,2017,38(4):195-203.

[17] KUREMOTO T, KIMURA S, KOBAYASHI K, et al. Time series forecasting using a deep belief network with restricted Boltzmann machines[J]. Neurocomputing,2014,137(15):47-56.

[18] TRAN V T, ALTHOBIANI F, BALL A. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaiser energy operator and deep belief networks[J]. Expert Systems with Applications,2014,41(9):4113-4122.

[20] XIE Zhijiang, LI Xingjun, LI Cheng, et al. Positive solution of 3-PPR parallel mechanism based on BP neural network with displacement compensation [J]. Computer Integrated Manufacturing Systems ,2015,21(7):1804-1809(in Chinese). [谢志江,李星君,李 诚,等.位移补偿BP神经网络的3-PPR并联机构的正解研究[J].计算机集成制造系统,2015, 21(7):1804-1809.]