特征地图中基于高斯核函数的自动导引车Markov定位算法

李 昊，叶文华，满增光

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

自动导引车(Automated Guided Vehicle, AGV)正越来越多地应用于智能物流与智能制造系统中，定位问题是AGV导航运动中的基本问题[1]。Markov定位算法即是一种常用于初始位姿未知情况下的AGV全局定位方法[2]，该方法基于概率状态分布，将对AGV位姿的估计看作多阶Markov过程，离散化的空间位姿即代表其中的状态变量。基于概率的定位方法能有效描述定位过程中的不确定性，其定位鲁棒性较好[3]，例如Markov定位方法不仅可以解决AGV被移动到新位置而产生的所谓“拐骗”问题[4-5]，还可以处理多模及非高斯分布的概率模型。在实际应用中，Markov定位方法可以基于任意一种形式的地图实现对AGV的全局定位[6]。对Markov定位的研究最早出现在基于拓扑地图的定位中[7]，其后被广泛应用于基于栅格地图的定位[8-9]。拓扑地图环境表示紧凑，便于实现快速搜索和路径规划，但无法表达拓扑节点以外的环境信息；栅格地图直观、易维护，但应用Markov定位时，其计算量与空间大小和分辨率有关，在空间范围大时其计算量通常较大，限制了地图精度的提高。

特征地图也是AGV常用的一种地图[10]，它以环境典型特征(如点、线等)作为地图表达形式，具有创建形式多样、空间信息表示高层次且简洁、对空间大小不敏感的特点。由于特征(路标)分布常具有稀疏性，在使用Markov方法对AGV定位时需要将观测数据与地图特征数据进行关联来计算观测模型[11]，而实际上，AGV自身携带的传感器探测环境时所得到的某一观测数据与地图特征的匹配常常不唯一，导致错误的数据关联[12]，使全局定位失败，因此Markov定位方法在特征地图中的研究应用较少，而针对特征地图目前也没有成熟有效的基于概率的全局定位方法[13]。

为提高Markov定位方法在基于特征地图时对AGV进行定位的有效性和实用性，使其能运用在实际运输作业中，本文提出一种基于高斯核函数拟合致密曲线的观测模型计算方法。因为特征在AGV极坐标系下的分布具有稀疏性，若直接运算，得到的则为二进制的离散值，限制了贝叶斯估计的作用，所以需要进行数据关联[14]；受数据关联方法使用的必要性启发，本文通过高斯核函数拟合AGV探测到的稀疏分散特征，得到包含这些特征的致密平滑曲线，使特征在AGV极坐标系下的分布由稀疏补为致密。高斯核函数是单值函数，具有旋转对称性、滤波器平滑程度可调等优点[15]，通过高斯核函数拟合特征点后观测模型的似然计算结果为连续值，对观测模型的计算即转变为对AGV实际观测与算法预测观测所拟合出的两条曲线相似度的计算，避免了特征地图中AGV观测与地图路标间的数据关联问题。将该计算方法用于Markov定位算法，可以在特征地图中实现对AGV的位姿估计与全局定位。

1 特征地图中的Markov定位算法

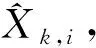
对全局定位问题而言，已知AGV的历史观测数据、运动控制输入和环境地图，k时刻AGV位姿估计可表示为

p(Xk|Z0:k,U0:k,M)。

(1)

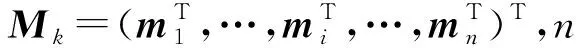
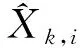
(2)

(3)

式中η=1/p(zk|Z0:k-1,U0:k)，在同一次估计中p(zk|Z0:k-1,U0:k)为常数。通过式(2)和式(3)的递归预测与校正递推计算可以估计初始位姿未知情况下AGV的当前位姿，实现AGV全局定位。

2 基于高斯核函数平滑的观测模型及算法

2.1 高斯核函数平滑方法

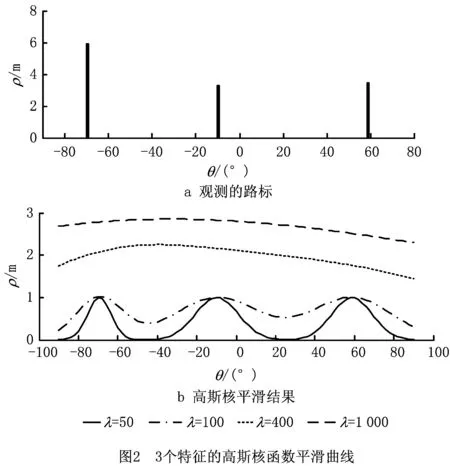
高斯核函数平滑原理如图1所示。以AGV在环境中观测到的3个特征为例，设为l1，l2和l3，分别对应极坐标系下的位置(ρ1,θ1)，(ρ2,θ2)，(ρ3,θ3)。若θ为自变量，ρ为θ的函数，则该函数为一个非连续、非平滑的函数。

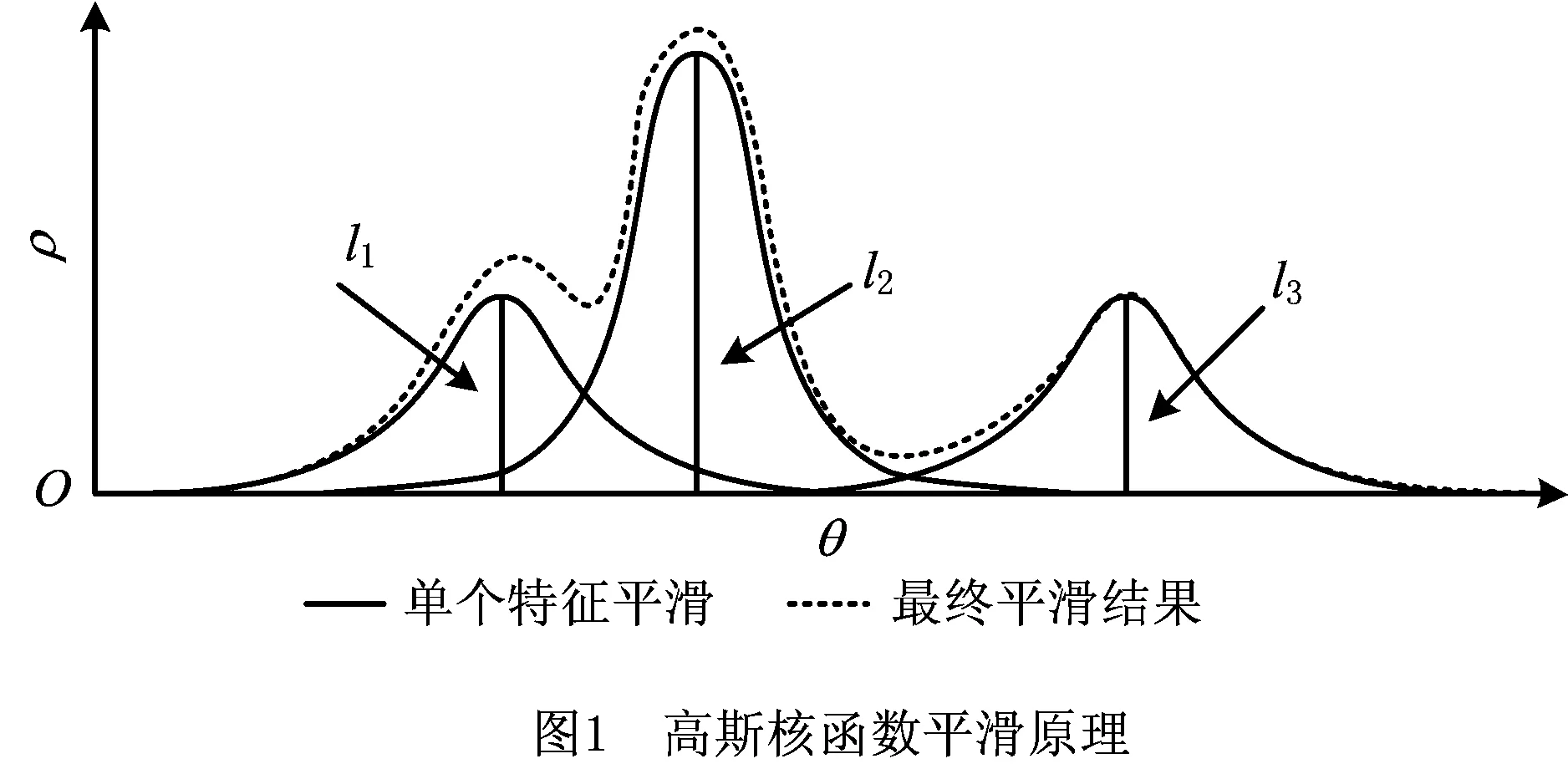
高斯核函数平滑方法即利用高斯核函数使ρ与θ间的关系呈现光滑连续性，可表示为

(4)

式中：K即高斯核函数；c为观测到的特征索引集合；σi为核带宽，σi=λ/ρi；λ为拟合平滑函数参数，通常大于0，其对拟合曲线的影响如图2所示，λ越大，曲线越平滑。

2.2 观测似然计算

通过上述高斯核函数平滑方法处理后，由传感器观测与算法预测的观测得到两条平滑函数曲线，再通过两者的离散化逐值比较来计算其相似度。转换的观测似然计算公式为

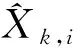
2.3 算法实现流程

基于高斯核函数的AGV Markov全局定位算法如下：

k=0；

End

While TRUE

k=k+1；

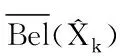
w=0；

End

End

End

3 仿真分析

为验证本文所提基于高斯核函数的观测似然计算构成的Markov定位方法的有效性，在MATLAB平台下进行了仿真分析，测距传感器为激光雷达传感器。按相似环境和非相似环境两种情况进行仿真，在相似环境下通过AGV直线行走的仿真来验证所提方法对AGV位姿估计的有效性；在非相似环境下通过AGV静止的仿真来验证所提方法对AGV位姿估计不但有效，而且高效。

3.1 相似环境下AGV运动定位的仿真

该仿真环境如图3所示，长宽均为20 m，设置4个特征点，特征点以5 m等间距分列在y=-2的直线上，设AGV初始时刻位于坐标原点，朝向与运动方向均平行于x轴，运动的线速度为1 m/s。传感器及算法相关参数如表1所示。

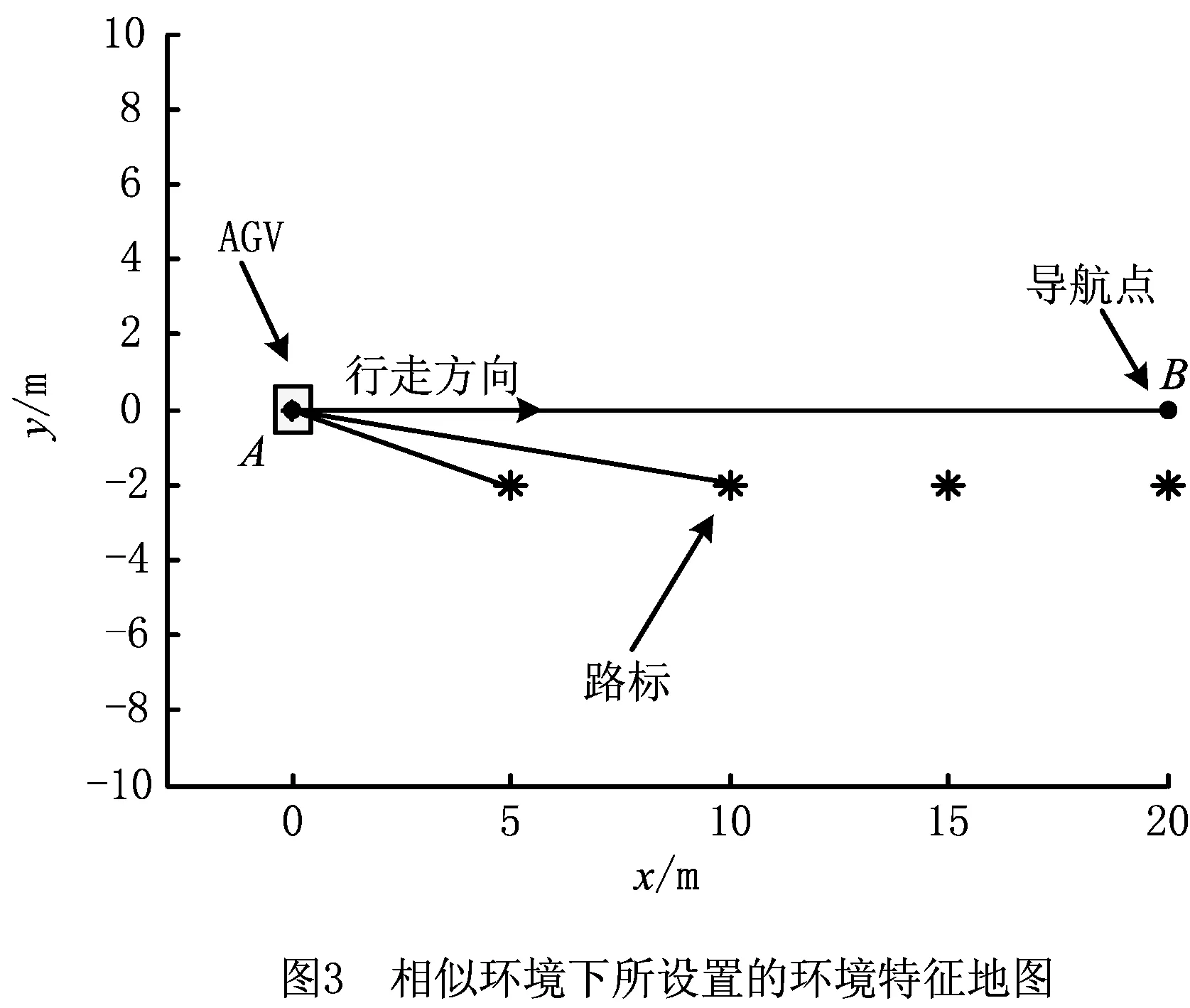
表1 传感器及算法参数设置

参数设定值激光测距传感器最远探测距离/m11激光测距传感器最大探测角度/(°)180离散化栅格大小/m20.2×0.2高斯核函数参数100

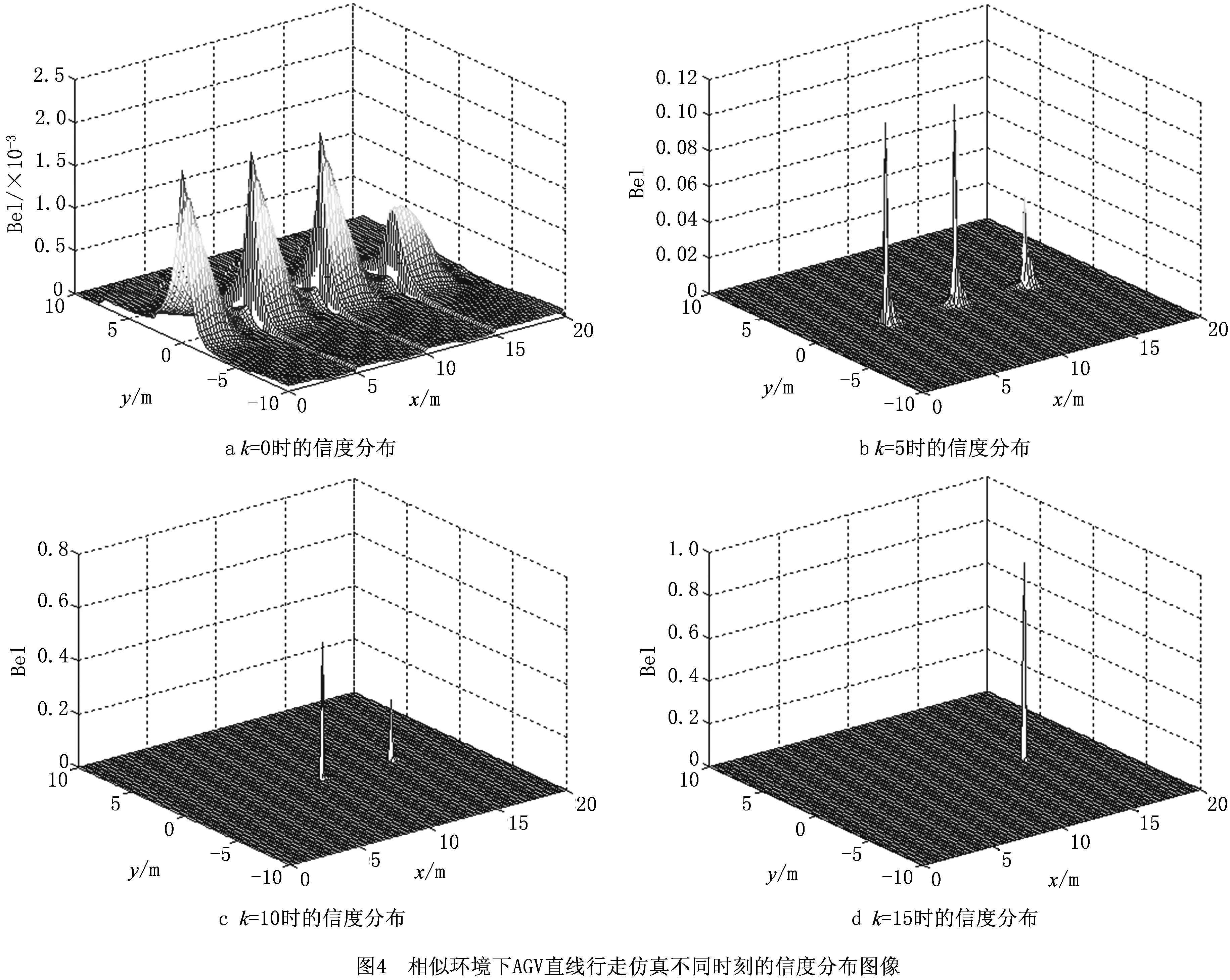
仿真所得信度分布结果如图4所示。从图4a可知，在初始k=0时刻，AGV的实际位置在(0,0)，计算各栅格被占有概率，得到(0,0)，(5,0)，(10,0)3个较大和(15,0)1个次大4个信度峰值坐标点，即AGV初始位置估计在这3个坐标附近。图4b～图4d分别为k=5，10，15时AGV在概率栅格中的位姿信度极值分布和变化情况。当k=15时，AGV的实际位姿为(15,0,0)，而信度栅格图像中只有(15,0)坐标存在信度极值，其他位置的概率信度均为0，即此刻已经正确估计出了AGV的位姿。从上述位姿信度的变化可知，随着AGV不断运动，感知到的特征信息不断增加，AGV从算法最初估计的多个坐标位置逐渐确定为唯一的真实坐标。以上结果表明AGV在直线行进时，本文所提的基于高斯核函数的Markov全局定位方法在特征地图中是有效的。

3.2 非相似环境下AGV静止定位的仿真

该仿真环境(如图5)的长宽均为10 m，设置40个随机分布的特征点。以a(2,2)，b(2,-2)，c(-2,2)，d(-2,-2)4个栅格整点作为AGV的初始放置坐标点，朝向如图5所示。传感器及算法相关参数如表2所示。

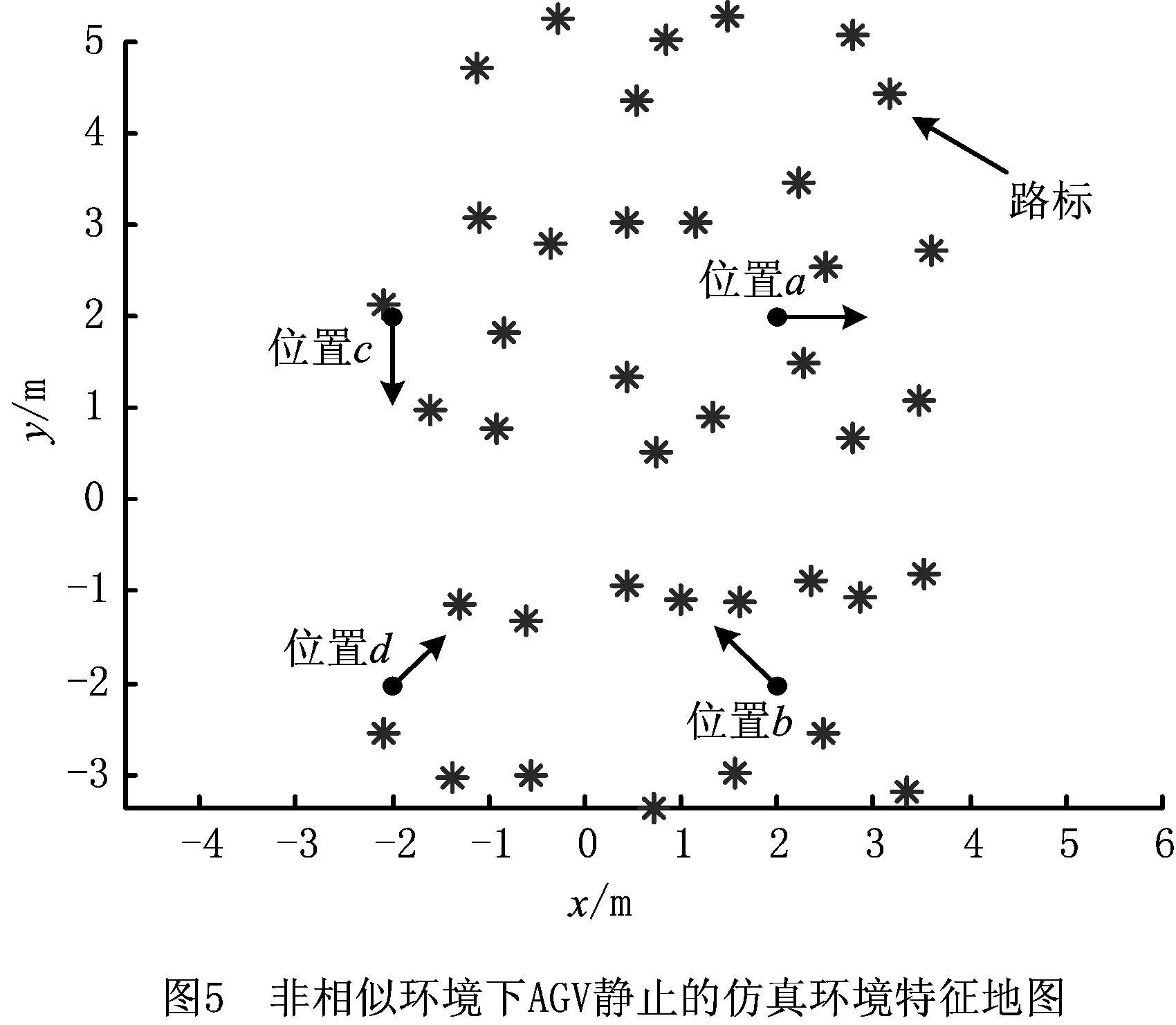
表2 传感器及算法参数设置

参数设定值激光测距传感器最远探测距离/m11激光测距传感器最大探测角度/(°)180离散化栅格大小/m20.1×0.1高斯核函数参数100

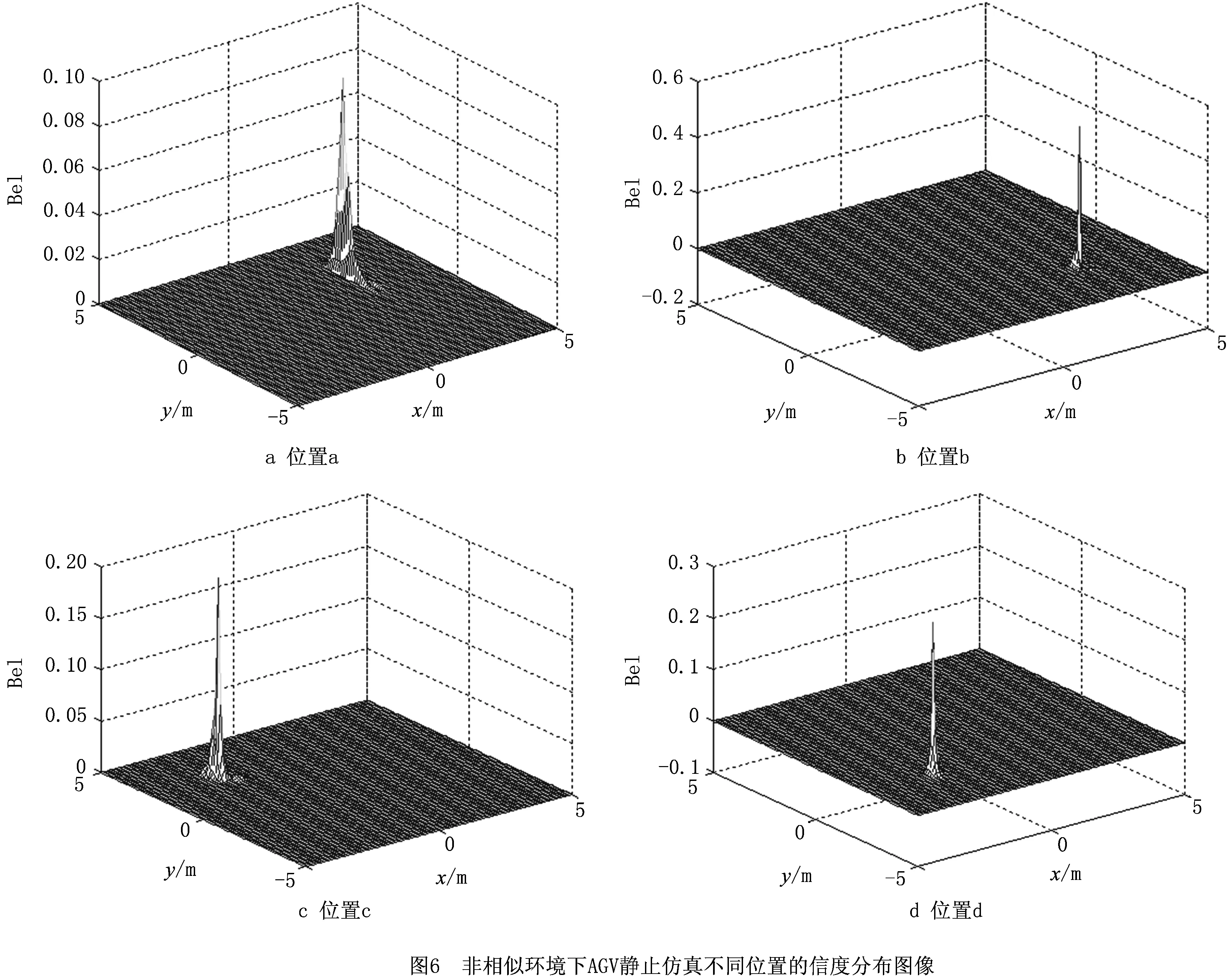
仿真所得信度分布结果如图6所示。图6a可知，AGV静止处于a位置时，位置信度图像中仅(2,2)坐标位置存在信度极值，即AGV只经过一次定位计算就将位置估计确定到真实坐标位置。图6b～图6d所示为AGV处于其他不同位置b，c，d时的仿真结果，与a位置结果相同，该仿真只经过一次定位计算即使AGV位置估计分别确定到真实坐标位置(2,-2)，(-2,2)和(-2,-2)。这说明在非相似环境中，将经过高斯核函数处理的Markov定位方法运用在特征地图中具有有效性和高效性。

4 实验验证

实验所用的AGV平台(如图7)长100 cm、宽60 cm、高40 cm。平台配备的传感器包括两个记录AGV运动信息的编码器和西克公司的LMS291-S05激光雷达测距传感器。真实环境如图8所示。为验证本文算法的有效性，首先通过对某一时刻的全局定位实验来验证算法对AGV位姿估计的准确性；然后采用ICP(iterated closest points)方法[16]估计的AGV位姿作为真实值，通过比较本文改进的Markov定位方法与常规Markov定位方法所得到的AGV运动轨迹来说明本文方法的优越性。实验中的特征路标采用从传感器数据中提取的环境角点与断点表示。

实验中AGV的行走路程为14.3 m，速度设置为0.1 m/s，运动时长280 s，使用AGV运动的前10 s传感器数据作为全局定位实验，离散化栅格尺寸为0.1 m×0.1 m。运动中AGV在环境中的位姿从(0,0,0)移至(0.604 7,0.020 4,-0.005 9)，算法运算时间为1.1 s。

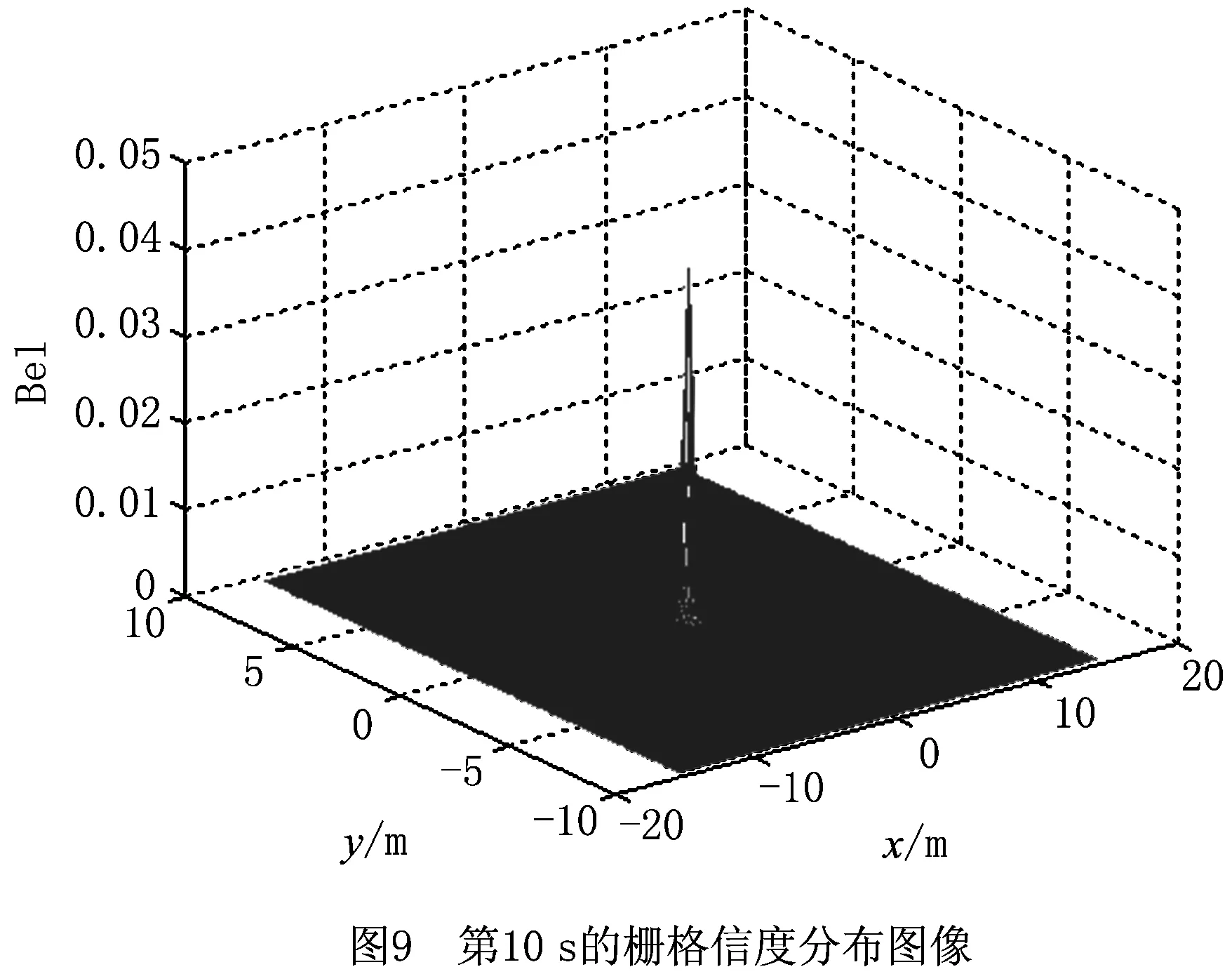
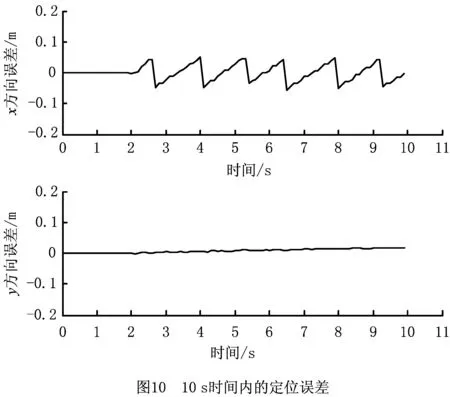
第10 s的AGV位置信度分布如图9所示，可见对AGV位姿的估计确定到了唯一一个信度极值点。10 s时间内的位置估计误差如图10所示，AGV在x方向上的位置估计误差不超过一个栅格边长0.1 m，在y方向上的位置估计误差接近于0且波动较小，证明本文方法在实际应用中是有效且准确的。

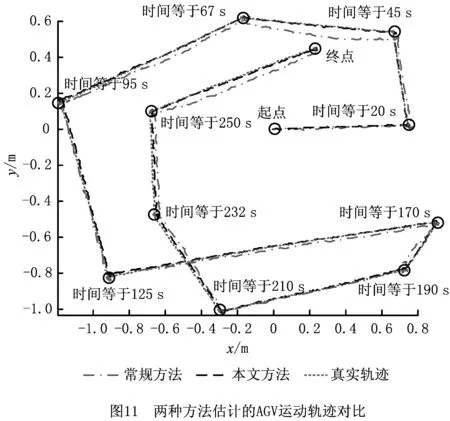
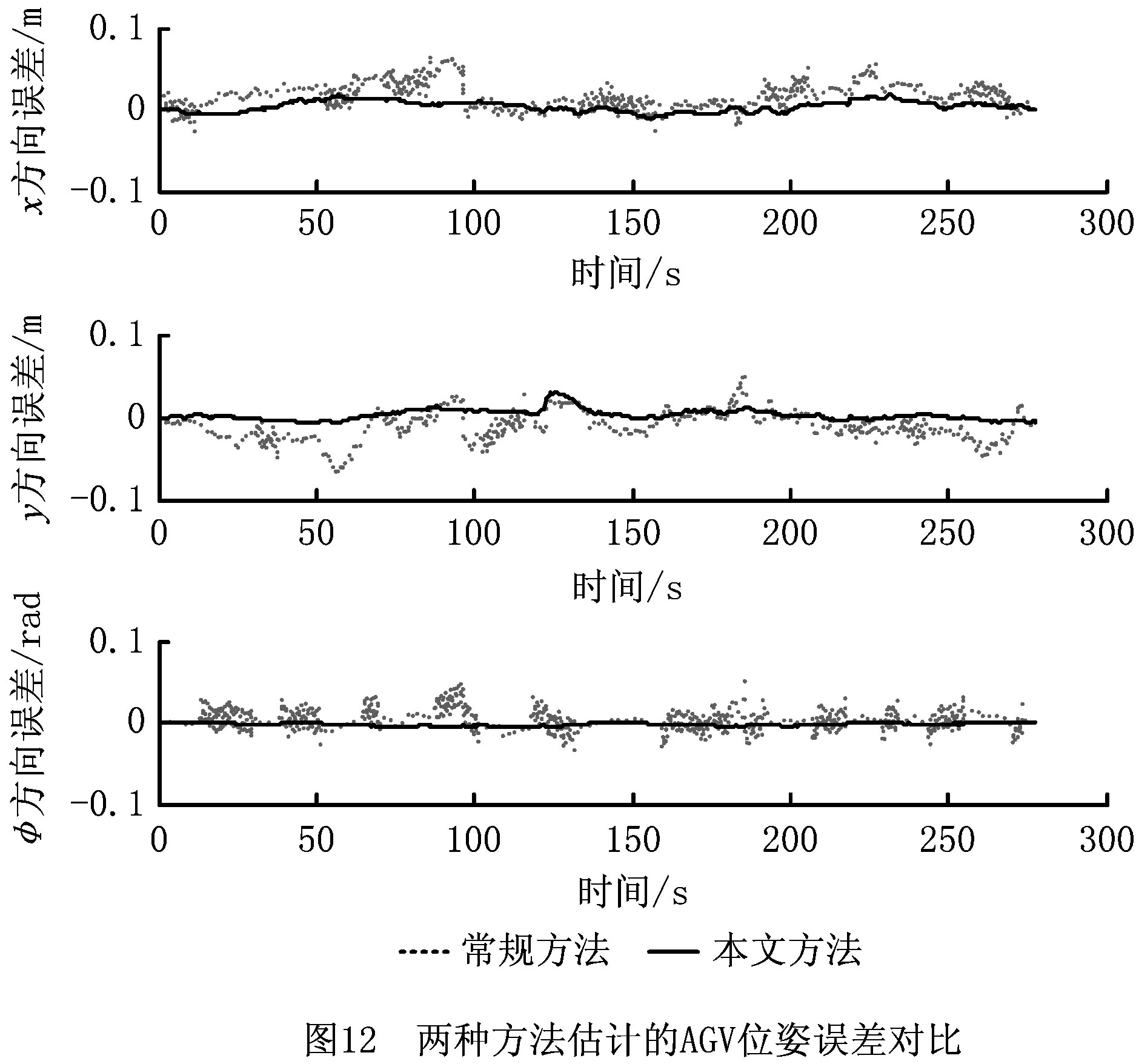
采用本文所提基于高斯核函数的Markov定位方法和常规使用的数据关联的Markov方法对AGV进行位姿跟踪，两者估计出的AGV运动轨迹如图11所示。从全局路径可以看出，本文所提定位方法对AGV位姿和轨迹的估计更接近真实轨迹，且大部分位置轨迹几乎重合，偏差很小；而常规方法估计出的AGV运动轨迹相比真实轨迹有一定偏移且轨迹偏移量不均匀。两种方法对AGV位姿估计的误差如图12所示，具体对比各时刻估计出的AGV位姿误差，显然本文方法对AGV在各方向上估计的位姿误差较小，相对真实位姿误差波动平缓；常规方法得到的位姿估计误差及误差波动相对更大。由此可见，本文方法对AGV在各方向上估计的位姿误差明显小于常规Markov方法，因此定位精度更高。

5 结束语

特征地图是AGV导航时常用的一种地图，其特征分布具有稀疏性，使用Markov方法定位时通常需要进行观测数据与地图间特征数据的关联，但常因观测与地图间匹配不唯一而导致错误的数据关联。本文提出的基于高斯核函数平滑和加密稀疏特征建立Markov全局定位观测模型及其计算方法，从本质上避免了在观测模型计算时对AGV观测与地图路标间进行的数据关联，提高了定位效率，且加入观测模型新计算方法的Markov定位算法能有效运用于特征地图中对AGV的全局定位，不仅提升了Markov定位在特征地图中的实用性，还对求解其他类型移动机器人在特征地图中的初始位姿有参考意义。同时，如何兼顾Markov定位方法的实时性与精度，使其有效应用于大规模环境，是下一步研究的内容。

参考文献:

[1] CUI Kangji, SUN Yu, ZHANG Xinning, et al. The research of accurate orientation technology for AGV[J]. Computer Integrated Manufacturing Systems,1995,1(4):39-41(in Chinese).[崔康吉,孙 宇,张新宁,等.AGV精确定位技术的研究[J].计算机集成制造系统，1995,1(4):39-41.]

[2] LIU Yu, ZHU Shiqiang, JIN Bo. Study on Markov localization algorithm for mobile robots:new modeling method for orientation sensor[J]. Journal of Zhejiang University:Engineering Science,2005,39(3):339-341(in Chinese).[刘 瑜,朱世强,金 波.移动机器人Markov定位算法的研究——方向传感器建模新方法[J].浙江大学学报:工学版,2005,39(3):339-341.]

[3] GAO Wei, SHAO Xiaodong, LIU Huanling. Automatic assembly location metion based on particle filter[J]. Computer Integrated Manufacturing Systems,2014,20(7):1615-1624(in Chinese).[高 巍,邵晓东,刘焕玲.基于粒子滤波的自动装配定位方法[J].计算机集成制造系统,2014,20(7):1615-1624.]

[4] ZHANG L, ZAPATA R, LEPINAY P. Self-adaptive Monte Carlo localization for mobile robots using range finders[J]. Robotica,2012,30(2):229-244.

[5] PENG Yanbin, AI Jieqing. Markov chain Monte Carlo method based bilateral multi-issue negotiation model[J]. Computer Integrated Manufacturing Systems,2011,17(9):2044-2050(in Chinese).[彭艳斌,艾解清.基于马尔可夫链蒙特卡罗方法的双边多议题协商模型[J].计算机集成制造系统,2011,17(9):2044-2050.]

[6] WU Qingxiang, Bell D. A study on Markov localization for mobile robots[J]. Acta Automatica Sinica,2003,29(1):154-160(in Chinese).[吴庆祥,D. Bell.可移动机器人的马尔可夫自定位算法研究[J].自动化学报,2003,29(1):154-160.]

[7] NOURBAKHSH I, POWER R, BIRCHFIELD S. DERVISH an office-navigating robot[J]. AI Magazine,1995,16(2):73-90.

[8] COLLINS T, COLLINS J J, MANSFIELD M, et al. Evaluating techniques for resolving redundant information and specularity in occupancy grids[C]∥Procedings of Australasian Jaint Conference on Artificial Intelligence. Berlin, Germany:Springer-Verlag,2005:235-244.

[9] BURGARD W, DERR A, FOX D, et al. Integrating global position estimation and position tracking for mobile robots:the dynamic Markov localization approach[C]∥Proceedings of the 1998 IEEE/RSJ International Conference on Intelligent Robots and Systems.Washington,D.C., USA:IEEE,1998:730-735.

[10] ZHU Jianguo, GAO Junyao, LI Kejie, et al. Research on feature map building of mobile robot in indoor unknown environment[J]. Computer Measurement & Control,2011,19(12)：3044-3046(in Chinese).[朱建国,高峻峣,李科杰,等.室内未知环境下移动机器人特征地图创建研究[J].计算机测量与控制,2011,19(12)：3044-3046.]

[11] MAN Zengguang. Research on mapping and localization of indoor AGV based on ladar[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2014(in Chinese).[满增光.基于激光雷达的室内AGV地图创建与定位方法研究[D].南京：南京航空航天大学,2014.]

[12] NEIRA J, TARDOS J D. Data association in stochastic mapping using the joint compatibility test[J]. IEEE Transactions on Robotics and Automation,2001,17(6):890-897.

[13] CHEN Guangzhong, CHEN Qingxin, MAO Ning, et al. Modeling and analysis of queuing network in manufacturing system with stochastic path AGV[J]. Computer Integrated Manufacturing Systems,2017,23(1):52-65(in Chinese).[陈冠中,陈庆新,毛 宁,等.具有随机路径AGV的制造系统排队网建模与分析[J].计算机集成制造系统,2017,23(1):52-65.]

[14] LI Yanju, XIAO Yufeng, GU Song, et al. Research on data association in SLAM based laser sensor[J]. Microcomputer & Its Applications,2017,36(2):78-82(in Chinese).[李延炬,肖宇峰,古 松,等.基于激光传感器的SLAM数据关联算法的研究[J].微型机与应用,2017,36(2):78-82.]

[15] LIN Hongbin, FU Demin, WANG Yinteng. Feature preserving denoising of scattered point cloud based on parametric adaptive and anisotropic Gaussian kernel[J]. Computer Integrated Manufacturing Systems, 2017,23(12):2583-2592(in Chinese).[林洪彬,付德敏,王银腾.基于参数自适应各向异性高斯核的散乱点云保特征去噪[J].计算机集成制造系统, 2017,23(12):2583-2592.]

[16] LI Congbo, XIAO Weihong, DU Yanbin, et al. Fine registration method for defective parts based on improved ICP algorithm[J]. Computer Integrated Manufacturing Systems,2016,22(4):1021-1028(in Chinese).[李聪波,肖卫洪,杜彦斌,等.基于改进ICP算法的损伤零部件精确配准方法[J].计算机集成制造系统,2016,22(4):1021-1028.]